面向雷達高速目標檢測的RFT快速實現方法

段 毅, 商哲然,2, 譚賢四, 曲智國, 李志淮

(1. 空軍預警學院防空預警裝備系, 湖北 武漢 430019; 2. 國防科技大學電子科學學院, 湖南 長沙 410073)

0 引 言

隨著具有高、快、小等特點的高超聲速目標的出現,傳統的雷達檢測技術遇到了嚴峻的挑戰[1-2]。通過補償脈沖間的相位變化來實現長時間相參積累可以顯著提高檢測性能[3-7]。但是,在相參積累時間內,目標高超聲速運動帶來的距離走動和多普勒模糊問題嚴重影響著傳統方法,如動目標檢測(moving target detection, MTD)的目標能量積累效果[8-11],必須消除上述影響以提高目標檢測性能。

近年來,學者們提出了一些新的檢測方法來解決目標回波包絡的距離走動問題,實現目標能量的有效積累,典型方法有校正補償類[12]的Keystone法[13-17]、相鄰交叉相關函數(adjacent cross correlation function,ACCF)[18-19]、序列反轉變換[20](sequence-reversing transform, SRT),搜索積累類[12]的Radon-Fourier變換(Radon Fourier transform,RFT)法[21-28]等。其中,RFT法有機地將MTD處理和Radon變換統一起來,直接沿目標初始距離和速度確定的直線軌跡對目標回波能量進行相參積累,取得了較好的檢測性能,但是標準RFT[21-23]存在運算量大、實時性差、量化損失大的缺點。針對上述不足,文獻[25, 29]提出了基于Chirp-Z變換(Chirp-Z transform, CZT)的RFT(CZT-RFT)算法。CZT-RFT算法的基本思想是,將RFT算法在頻域利用CZT實現,從而顯著提高了算法的運算速度和能量積累效果。但是,當存在多普勒模糊時,該方法需要對多普勒模糊數進行遍歷搜索并作補償處理,然后對多次補償后的積累結果進行選大處理,以得到最終積累結果。當多普勒模糊數較大時,CZT-RFT算法的運算量將急劇增大;此外,多個補償積累結果之間的選大處理在得到最大目標積累能量的同時也抬高了噪聲電平,影響了檢測性能。而現有警戒雷達,特別是地面警戒雷達,通常采用低重頻工作模式,當探測以5～20 Ma速度飛行的高超聲速目標時,多普勒模糊數將非常大,導致算法運算量急劇增加,上述方法難以直接應用。

為了解決上述問題,本文提出了一種改進的RFT快速實現方法——由粗到精(coarse-to-fine,CTF)的RFT算法(CTF-RFT),該方法采用CTF逐步縮小搜索范圍的策略確定目標的多普勒模糊數,進而獲得最終的目標能量積累結果,實現目標檢測并確定目標的精確參數。與文獻[25,29]的方法相比,該方法進一步降低了運算量,并解決了選大處理帶來的噪聲電平抬高的問題。理論分析和實驗結果驗證了本文方法的有效性。

1 RFT算法

假設雷達發射線性調頻(linear frequency modulation,LFM)信號,考慮目標作高速勻速運動,則脈沖壓縮后的回波信號可表示為

(1)

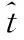
1.1 標準RFT算法

RFT是一種廣義的MTD[21]。假設目標軌跡可由目標的初始距離和速度構成的二維坐標(R0,vr)決定,如圖1(a)所示。RFT的變換公式為

(2)

由式(2)可知,當(R0,vr)=(R0i,vri)時,即搜索參數等于目標的真實參數時,則g(R0i,vri)出現峰值,如圖1所示。

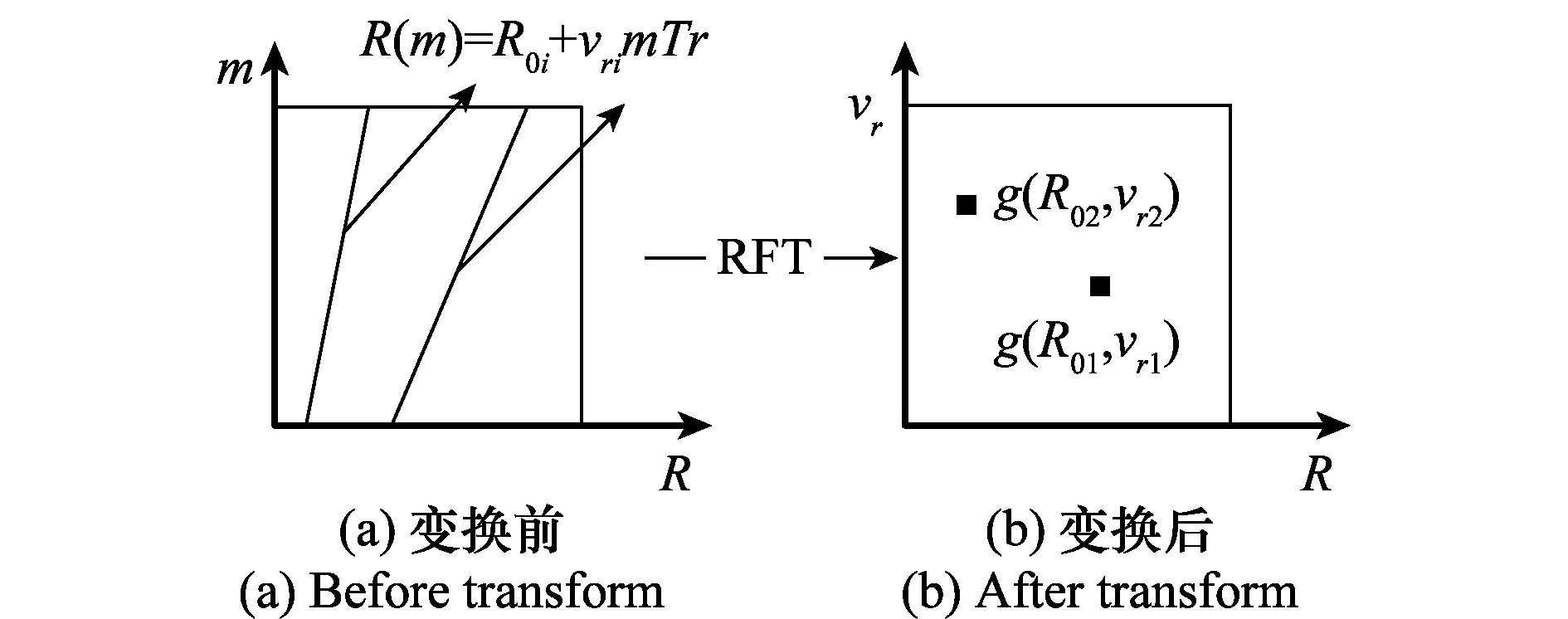
圖1 RFT原理Fig.1 Principle of RFT

式(2)中的速度參數vri起到兩個作用:一是決定了直線的斜率,即RFT沿哪條軌跡進行能量積累;二是對式(1)中的第2個指數項進行相位補償,實現相參積累。一般來說,警戒雷達脈沖重復頻率(pulse repetition frequency,PRF)fr較低,導致出現速度(或多普勒)模糊。令vr為目標真實徑向速度,v0為目標的模糊速度,k0為多普勒模糊數,vb=λfr/2為第一盲速,則真實速度與模糊速度、盲速之間的關系為

vr=v0+kvb

(3)

當目標真實速度vr在[-vrmax,vrmax]內變化時,其模糊速度v0始終在[-vb/2,vb/2]中變化,多普勒模糊數k在[-Kmax,Kmax]間取值,使得回波的多普勒相位在不同模糊數的對應速度上都能得到補償,但由于非真實模糊數k≠k0對應的積分直線不是目標的真實軌跡,積累的峰值只是目標的部分能量,使得RFT積累結果中沿速度維出現了周期性的盲速副瓣,周期為PRF對應的速度范圍稱為盲速區間,如圖2所示。標準RFT算法在速度維[-vrmax,vrmax]進行窮盡搜索,導致算法運算量大。

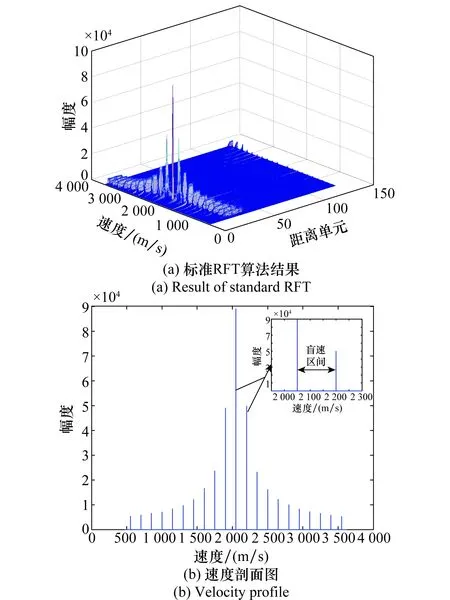
圖2 RFT積累結果示意圖Fig.2 Result of RFT

1.2 CZT-RFT算法

CZT-RFT將整個速度搜索范圍[-vrmax,vrmax]分解為2Kmax個不同多普勒模糊數對應的盲速區間,在單個盲速區間[-vb/2,vb/2]上利用CZT變換快速實現RFT算法,然后遍歷2Kmax個多普勒模糊數并進行補償處理得到2Kmax個積累結果,再對2Kmax個盲速區間的積累結果進行選大處理[7],得到最終積累結果以檢測目標。

在單個盲速區間,CZT-RFT實現如下:

(4)

(5)

(6)

式(4)可通過CZT快速實現,式(5)可通過快速傅里葉逆變換(inverse fast Fourier transform,IFFT)實現。

CZT-RFT算法提高了單個盲速區間內的RFT運算速度,但多普勒模糊數較大時,需要對多普勒模糊數進行遍歷搜索補償,而每次補償都需要計算一次CZT-RFT,導致算法運算量隨著多普勒模糊數的增加迅速增大。而地面警戒雷達通常采用低PRF工作,當探測高速目標時(5～20 Ma),目標速度對應的模糊數非常大,需要進行多次補償,降低了算法的實時性能。另外,多個不同多普勒模糊數對應的積累結果之間的選大處理,在得到目標最佳積累能量的同時也抬高了目標周圍的噪聲電平,影響了目標的檢測性能,增加了后續恒虛警率檢測(constant false alarm rate,CFAR)[30]處理的難度,如圖3所示。

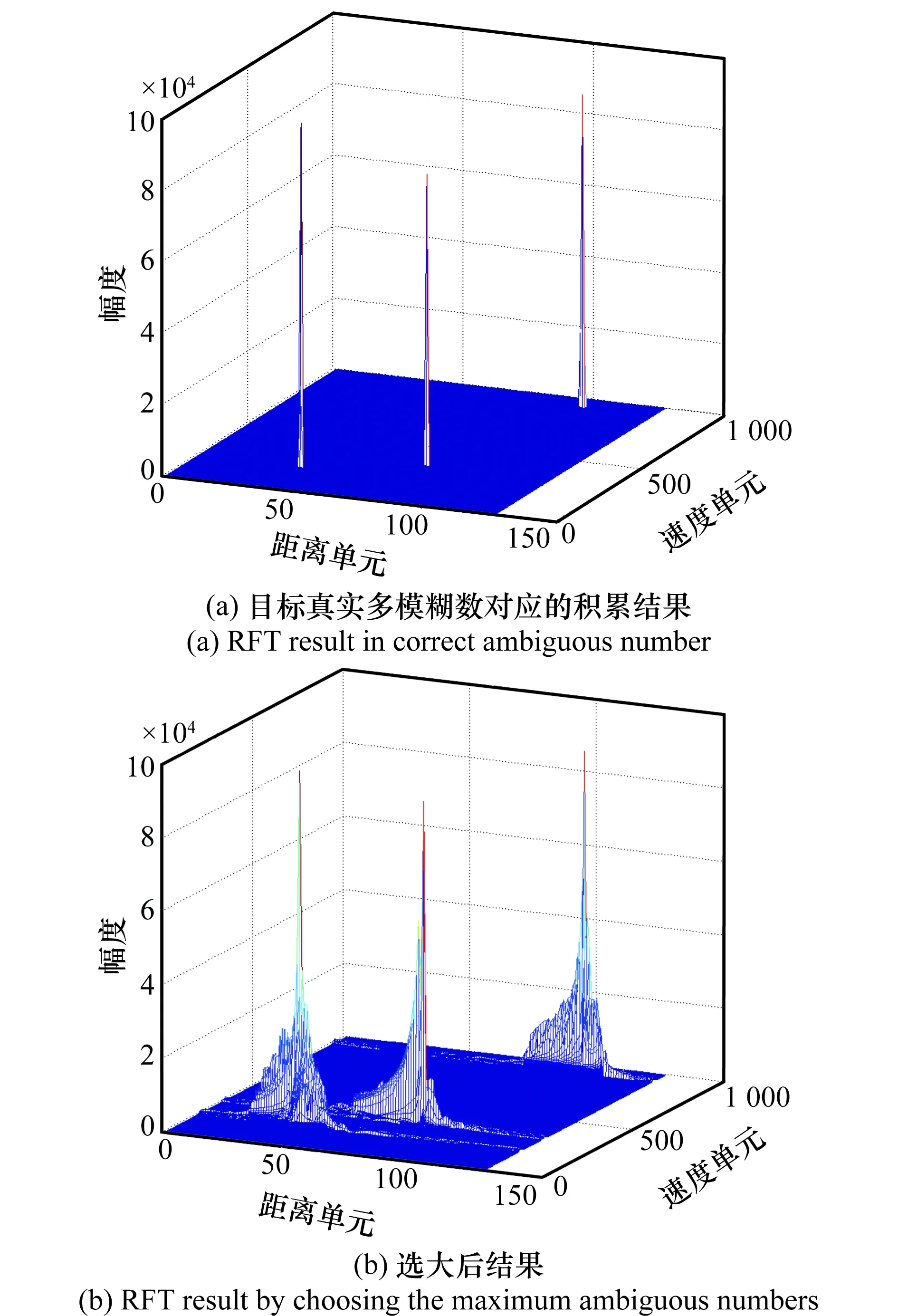
圖3 多個多普勒模糊數選大處理的RFT積累結果Fig.3 RFT result by choosing the maximum from multiple ambiguous numbers

2 CTF-RFT快速算法

2.1 基本思想

CZT-RFT算法將標準RFT算法分解為單個盲速區間上G(R,v)的能量積累和多普勒模糊數k的窮盡搜索以及選大處理。只有當搜索參數與目標的真實參數完全相同時,即R=R0,v=v0,k=k0時才出現最大峰值,即主瓣。但根據式(3)及圖2可知,當搜索的多普勒模糊數不等于目標的多普勒模糊數k≠k0時,在G(R0,v0)處也會形成峰值,即副瓣,主副瓣峰值比(primary lobe-to-sidelobe ratio， PSLR)[22,26]為

(7)

式中,λ為波長;M為脈沖積累個數;ρr為距離分辨率。

假設參數取值為λ=0.3 m,脈沖數M=1 000,目標速度為v=2 050 m/s,圖4(a)給出了主副瓣峰值比PSLR與主副瓣模糊數之差Δk=|k-k0|之間的關系;令Δk=|k-k0|分別取1,2,3,圖4(b)給出了PSLR隨距離分辨率ρr的變化關系。由圖4可以看出:PSLR與Δk=|k-k0|符合式(7)的變化規律,PSLR與Δk=|k-k0|成正比,與ρr成反比。在主瓣峰值一定的情況下,副瓣峰值與Δk=|k-k0|成反比、與ρr成正比,隨Δk單調變化,ρr越大、與真實多普勒模糊數的差值Δk=|k-k0|越小,則多普勒模糊數k對應的盲速區間積累的副瓣峰值越高。另外,由圖4還可以看出,當雷達的距離分辨率較低時,如當ρr=150 m時,Δk=1,2時的主副瓣比分別為1.7,2.9,也即相鄰多普勒模糊數下積累的副瓣峰值僅比真實多普勒模糊數下積累的峰值低2.3 dB,4.6 dB,而且當距離分辨率降低時,這一數值還將進一步降低。這就啟示我們,可以在損失很小信噪比的前提下對多普勒模糊數進行跨間隔搜索(Δk=1對應搜索間隔為3,Δk=2對應搜索間隔為5),從而避免了多普勒模糊數遍歷搜索帶來的冗余運算量。

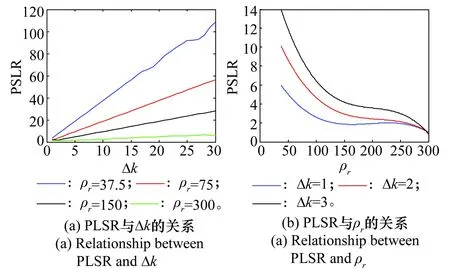
圖4 主副瓣比變化規律Fig.4 Relationship between PLSR and Δk、ρr

2.2 算法實現

CTF-RFT檢測算法的主要思路是,在多普勒模糊數維上進行跨間隔搜索,以降低運算量;并根據目標積累能量隨多普勒模糊數之差Δk的單調變化規律來剔除虛假目標,以提高檢測性能。

在粗檢測階段,首先對多普勒模糊數進行跨間隔粗搜索,然后基于CZT-RFT方法得到不同模糊數下目標在距離-多普勒維二維平面上的積累結果;然后對不同模糊數下的多個二維積累平面進行粗檢測提取潛在目標,并將潛在目標的積累能量幅度沿模糊數維排列,通過比較同一潛在目標沿模糊數維的幅度變化規律來進一步剔除虛警,確定目標所在的模糊數區間和粗略參數;在精檢測階段,對于潛在目標所在大區間內的模糊數進行精細搜索,檢測目標確定目標的精確參數。CTF-RFT算法具體實現流程如圖5所示,主要包括以下幾個步驟。

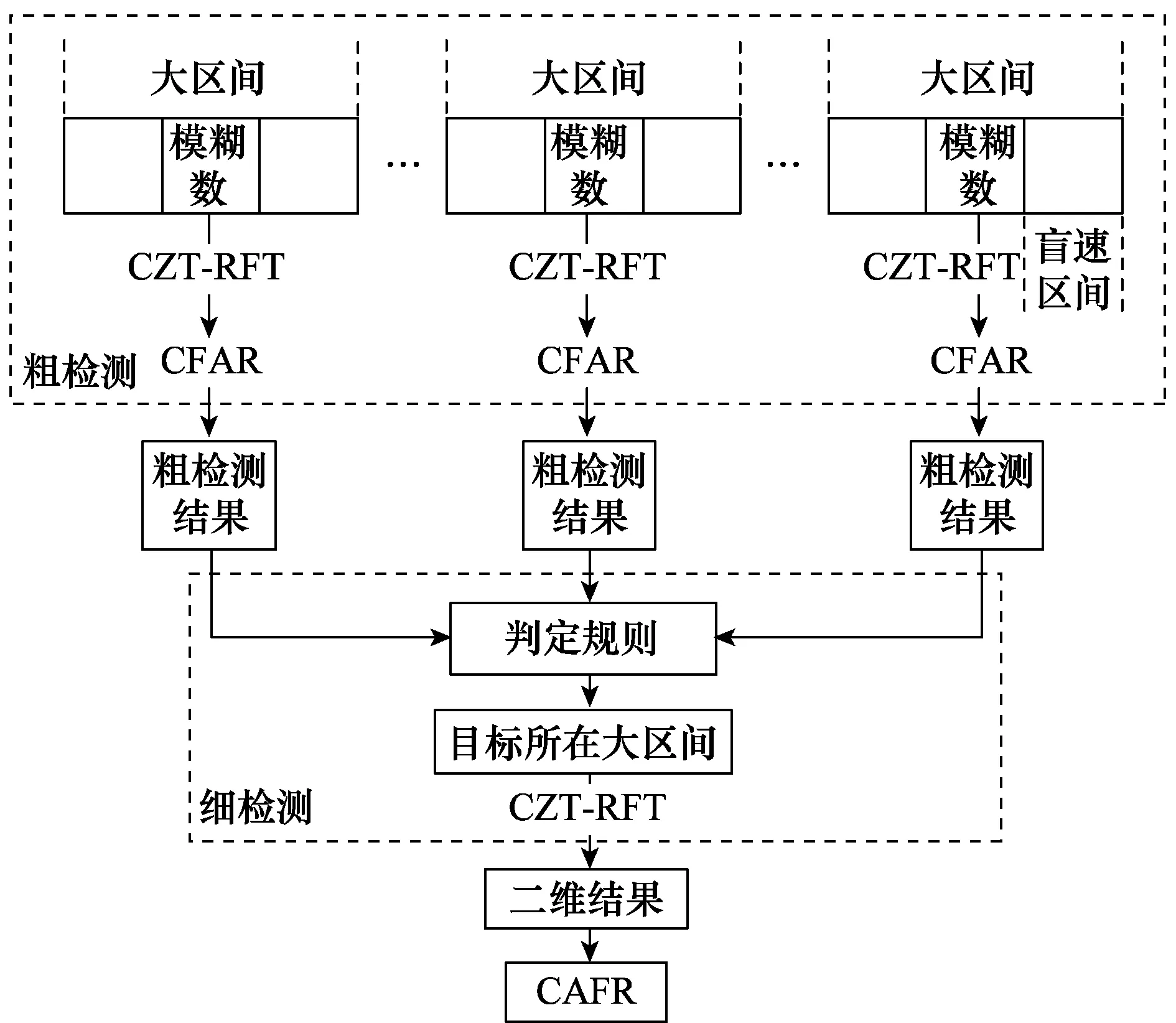
圖5 CTF-RFT算法流程Fig.5 Flowchart of CTF-RFT

步驟1搜索區間劃分。令Δl為多普勒模糊數的搜索間隔,若待搜索的多普勒模糊數區間為[-Kmax,Kmax],則將待搜索多普勒模糊數區間劃分成(2Kmax+1)/Δl個大區間,依次編號為

I=[-Kmax/Δl],[-Kmax/Δl]+1,…,[Kmax/Δl]

式中，[·]表示取整運算。

步驟2積累能量計算。對于每個大區間I,取中心多普勒模糊數作為該區間的典型值,利用CZT-RFT方法計算目標能量在距離-速度二維平面上的能量積累結果gI(r,v)。

步驟3粗檢測提取潛在目標。采用CFAR處理對得到的(2Kmax+1)/Δl個距離-速度二維積累結果gI(r,v)進行粗檢測,提取出潛在目標,并記錄相關參數信息,如幅度、距離、速度等信息。

步驟4潛在目標確認。將在距離-速度二維平面上位置相同的潛在目標的積累能量幅值沿多普勒模糊數維排列,根據副瓣峰值隨Δk的單調變化規律確認目標。

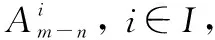
?i1,i2∈[imax-ΔI,imax+ΔI],|i1-imax|<|i2-imax|時

(8)

若式(8)成立,則確認該潛在目標為真實目標,并得到imax為該目標所在的多普勒模糊數大區間。

步驟5精搜索確定精確參數。對于確認目標的多普勒模糊數大區間imax內的每個模糊數進行CZT-RFT計算,得到二維積累結果后進行CFAR處理得到目標的精確參數。

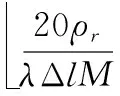
2.3 算法性能分析

CTF-RFT算法采用跨間隔搜索多普勒模糊數,極大地降低了CZT-RFT方法的運算量,但同時也帶來了一定的信噪比損失。下面從信噪比損失和運算量兩方面分析算法的性能。

由圖5可見,以Δl為間隔對多普勒模糊數進行粗搜索時,當目標真實多普勒模糊數不在大區間的中心模糊數上時,其積累峰值會降低,導致帶來信噪比損失。由于目標的多普勒模糊數在每個大區間上服從均勻分布的,根據式(7),跨間隔搜索帶來的信噪比損失為

(9)

令N,M分別表示采樣單元數和脈沖積累數。對于CZT-RFT算法,單次CZT-RFT需要乘法次數為(3+log2M)NM,單次Global-CFAR求均值需加法次數為NM-1[31]。當遍歷搜索多普勒模糊數,CZT-RFT算法總的運算量為

(2Kmax+1)(3+log2M)NM

而CTF-RFT的運算量為

式中,It為所有目標速度落入的大區間個數。

則兩種算法運算量之比為

(10)

在N=128,M=1 000參數下,運算量之比與信噪比損失關系如圖6所示。可以看出,信噪比的損失換來了運算量的降低。另外,在損失相同信噪比的前提下,搜索的多普勒模糊數越多,與CZT-RFT相比減少的運算量越多。

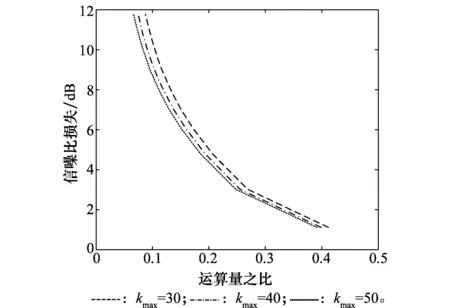
圖6 運算量之比與信噪比損失關系Fig.6 Relationship between ratio of computation and SNR loss

3 實驗結果與分析

采用仿真實驗分析CTF-RFT的性能,并與CZT-RFT算法進行比較。實驗環境為:計算機CPU為i7-3370,主頻3.4 GHz,內存為16 GB,Matlab8.3。

雷達和目標參數為:fc=1 GHz,B=1 MHz,Tp=127 μs,fs=1 MHz,fp=1 000 Hz,ρr=150 m,積累處理時間為TCIT=1 s。目標速度vT1=570 m/s,vT2=1 060 m/s,vT3=2 050 m/s,初始相對距離單元為40,100,80,對應模糊數為8,15,28,Δl=3,ΔI=3,Kmax=30。目標距離走動情況如圖7所示。

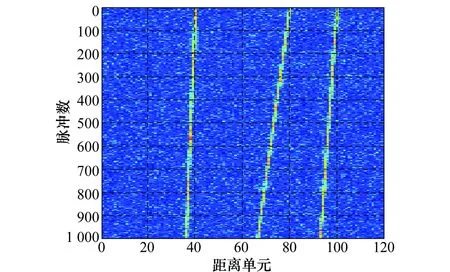
圖7 目標距離走動示意圖Fig.7 Illustration of across range unit (ARU)

3.1 實驗1

實驗1旨在驗證CTF-RFT算法的性能。圖8為本文方法的粗檢測示意圖,其中圖8(a)為補償多普勒模糊數等于15時的積累結果,圖8(b)為對圖8(a)進行粗檢測得到的結果。

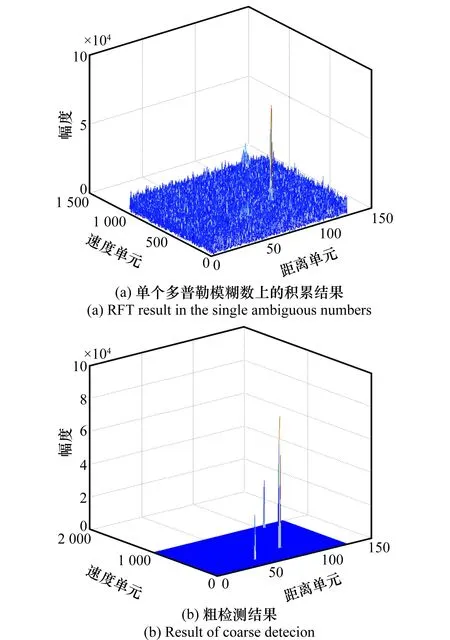
圖8 CTF-RFT粗檢測結果Fig.8 Coarse detecion of CTF-RFT

對多個不同大區間上的多普勒模糊數補償后進行粗檢測得到多個潛在目標,將同一距離單元、同一速度單元上的多個潛在目標的積累能量沿多普勒模糊數維進行排列,如圖9所示。

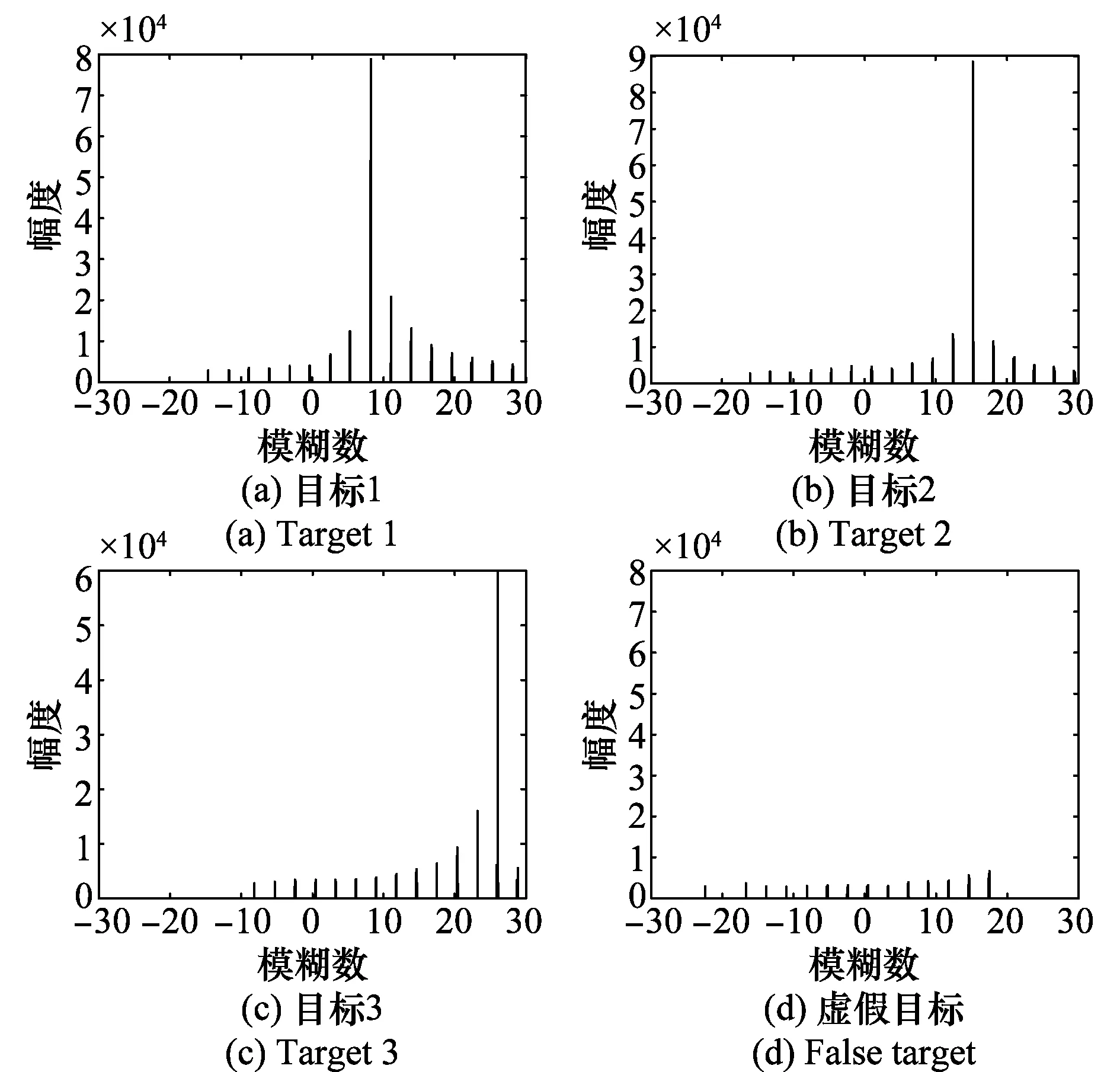
圖9 潛在目標的積累能量在多普勒模糊數維的變化規律Fig.9 Variation of potential targets on dimension of Doppler ambiguous number

由圖9可以看出,真實目標的積累能量沿著多普勒模糊數的變化規律與圖2分析一致,采用式(8)的判定規則可消除虛假目標,檢測出真實目標。通過對真實目標積累能量最大的大區間進行進一步精細搜索可以得到最終結果,如圖10所示。

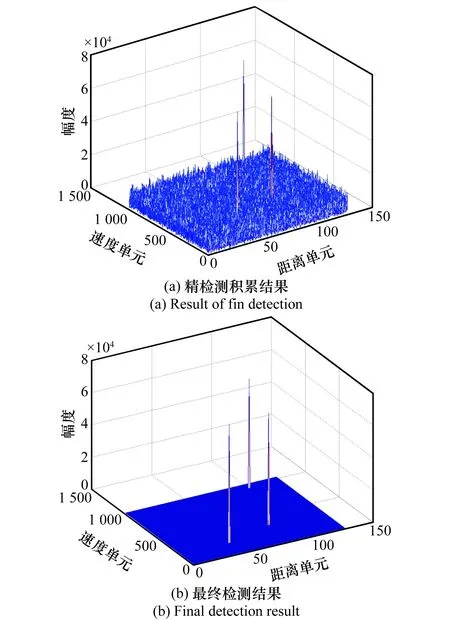
圖10 CTF-RFT精檢測結果Fig.10 Fine detecion results of CTF-RFT

3.2 實驗2

實驗2比較CTF-RFT和CZT-RFT的檢測性能和時間性能。

仿真參數不變,以目標3為例,假設其速度在區間[2 025,2 175]m/s隨機取值。設定虛警概率為Pfa=10-6,圖11給出了經過2 000次蒙特卡羅仿真得到的檢測概率Pd與信噪比SNR的關系,圖12給出了兩種算法在不同盲速區間數量下的平均耗時。

由實驗結果可以看出,CTF-RFT取得了與CZT-RFT算法幾乎相同的檢測性能,但是其平均耗時僅為CZT-RFT的0.412倍(搜索盲速區間為61時)。由圖12還可以看出,當目標的多普勒模糊數越大時,也即待搜索的盲速區間數量越大時,與CZT-RFT算法相比,CTF-RFT算法節省的運算量也就越多。另外,實驗中我們設定多普勒模糊數的搜索間隔為Δl=3,當增大搜索間隔Δl時,可以進一步降低算法運算量,但同時也會帶來一定的檢測性能損失。

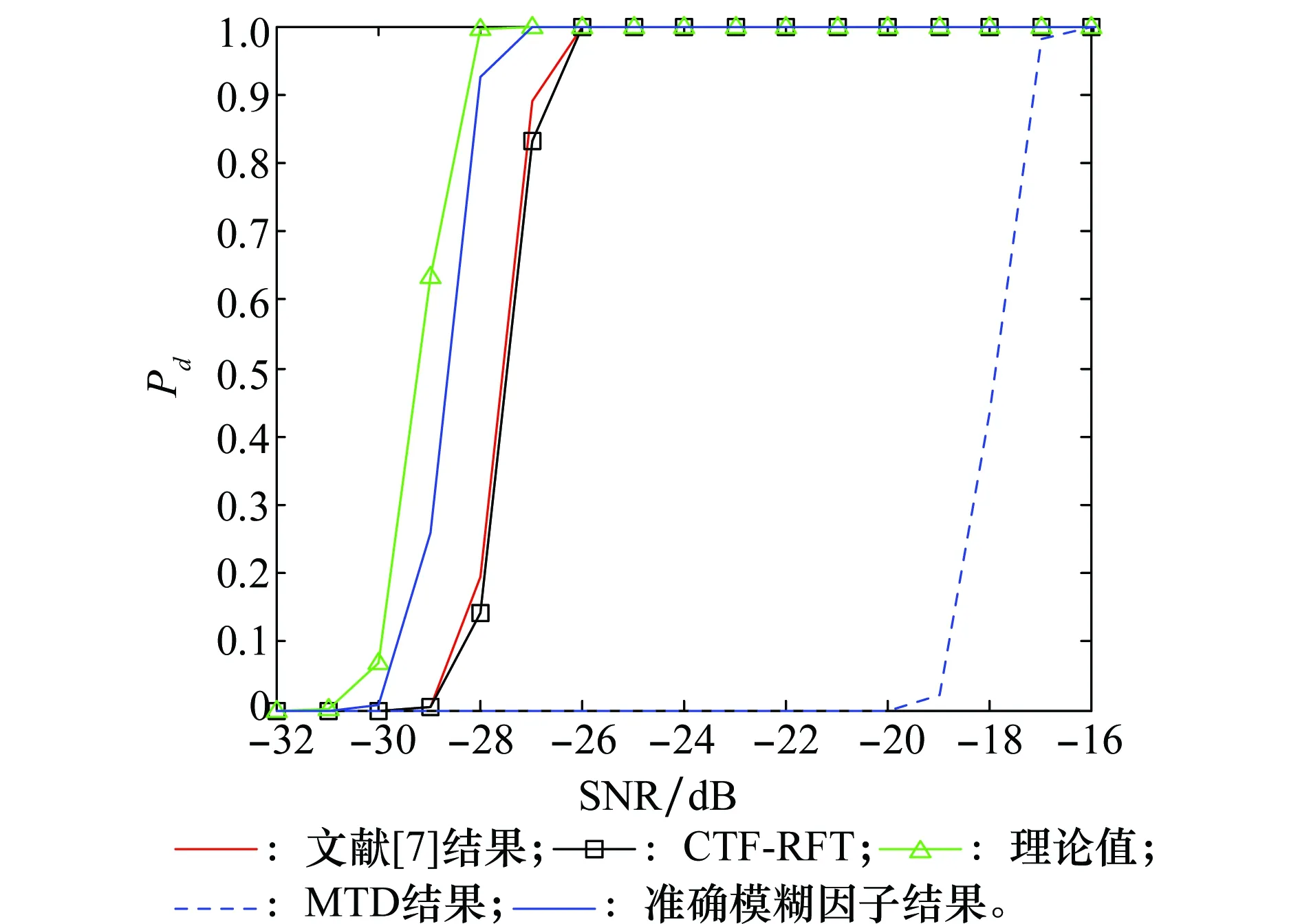
圖11 虛警概率為10-6時目標3檢測概率Fig.11 Pd of target 3 with Pfa=10-6

圖12 兩種算法耗時統計Fig.12 Time consumption of CZT-RFT and CTF-RFT

4 結束語

本文提出了一種CTF-RFT算法,采用對多普勒模糊數跨間隔搜索的策略來降低CZF-RFT算法的運算量,算法分為粗檢測和精檢測兩個階段,粗檢測完成潛在目標的提取和參數的粗略估計,精檢測消除虛警并最終檢測出目標,得到目標的準確參數。理論分析與仿真實驗表明,與CZT-RFT相比,CTF-RFT在幾乎不降低檢測性能的同時,進一步減少了運算量。另外,通過對CTF-RFT中模糊數搜索間隔的靈活調整可進一步提高CTF-RFT算的運算速度。

參考文獻：

[1] 戰立曉,湯子躍,朱振波. 一種米波相控陣雷達四代機目標檢測算法[J]. 電子與信息學報,2013,35(5): 1163-1169.

ZHAN L X, TANG Z Y, ZHU Z B. The fourth generation fighters detection algorithm for metric-band phased array radar[J].Journal of Electronics and Information Technology,2013,35(5):1163-1169.

[2] 勒松陽. 臨近空間高速機動目標檢測技術研究[D]. 西安: 西安電子科技大學, 2014.

LE S Y. Research on detection methods of high-speed maneuvering target in near space[D]. Xian: Xidian University, 2014.

[3] XING M D, SU J H, WANG G Y, et al. New parameter estimation and detection algorithm for high speed small target[J]. IEEE Trans.on Aerospace Electronic System, 2011, 47(1): 214-224.

[4] RAO X, TAO H H, SU J, et al. Axis rotation MTD algorithm for weak target detection[J].Digital Signal Processing,2014,26(1): 81-86.

[5] LI X L, CUI G L, YI W, et al. Coherent integration for maneuvering target detection based on Radon-Lv’s distribution[J].IEEE Signal Processing Letters, 2015, 22 (9): 1467-1471.

[6] SU J, XING M, WANG G, et al. High-speed multi-target detection with narrow band radar[J].IET Radar Sonar Navigation, 2010,4(4):595-603.

[7] CHEN X L, HUANG Y, LIU N B, et al. Radon-fractional ambiguity function-based detection method of low-observable maneuvering target[J]. IEEE Trans.on Aerospace and Electronic Systems, 2015, 51(2): 815-833.

[8] TAO R, ZHANG N, WANG Y. Analysing and compensating the effects of range and Doppler frequency migrations in linear frequency modulation pulse compression radar[J].IET Radar Sonar Navigation, 2011, 5(1): 12-22.

[9] PANG C, TAO S, TAO R, et al. Detection of high-speed and accelerated target based on the linear frequency modulation radar[J].IET Radar Sonar Navigation, 2014, 8(1): 37-47.

[10] LI X L, CUI G L, YI W, et al. Range migration correction for maneuvering target based on generalized keystone transform[C]∥Proc.of the IEEE Radar Conference, 2015: 95-99.

[11] HUANG P H, LIAO G S, YANG Z W, et al. An approach for refocusing of ground fast-moving target and high-order motion parameter estimation using radon-high-order time-chirp rate transform[J]. Digitial Signal Processing, 2016, 48(C): 333-348.

[12] 商哲然,譚賢四,曲智國,等.高超聲速目標雷達檢測方法綜述[J].現代雷達,2017, 39(1):1-8.

SHANG Z R, TAN X S, QU Z G, et al. Review on radar detection technology of hypersonic targets[J]. Modern Radar, 2017, 39(1): 1-8.

[13] PERRY R P, DIPIETRO R C, FANTE R L. SAR imaging of moving targets[J]. IEEE Trans.on Aerospace Electronic Systems, 1999, 35(1): 188-200.

[14] ZHU D Y, LI Y, ZHU Z D. A keystone transform without interpolation for SAR ground moving-target imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4 (1): 18-22.

[15] LI G, XIA X G, PENG Y N. Doppler keystone transform: an approach suitable for parallel implementation of SAR moving target imaging[J].IEEE Geoscience and Remote Sensing Letters, 2008, 5 (4): 573-577.

[16] YUAN S J, WU T, MAO M, et al. Application research of keystone transform in weak high-speed target detection in low-PRF narrowband chirp radar[C]∥Proc.of the 9th International Conference on Signal Processing, 2008: 2452-2456.

[17] 柏業超,高玉祥,張興敢.基于Keystone變換的高速運動目標檢測方法研究[J].南京大學學報(自然科學),2014,50(1):30-34.

BO Y C, GAO Y X, ZHANG X G. Rearch on high-velocity targets detection based on keystone transform[J].Journal of Nanjing University (Natural Sciences). 2014, 50(1): 30-34.

[18] LI X L, CUI G L, YI W, et al. A fast maneuvering target motion parameters estimation algorithm based on ACCF[J]. IEEE Signal Processing Letters, 2015, 22(3): 270-274.

[19] LI X L, CUI G L, KONG L J, et al. Fast non-searching method for maneuvering target detection and motion parameters estimation[J].IEEE Trans.on Signal Processing,2015,63(10):1-33.

[20] LI X L, CUI G L, YI W, et al. Sequence-reversing transform-based coherent integration for high-speed target detection[J].IEEE Trans.on Aerospace and Electronic Systems, 2017,53(3): 1573-1580.

[21] XU J, YU J, PENG Y N, et al. Radon-fourier transform for radar target detection, I-generalized Doppler filter bank[J].IEEE Trans.on Aerospace and Electronic,2011,47(2):1183-1202.

[22] XU J, YU J, PENG Y N, et al. Radon-Fourier transform for radar target detection (II) blind speed sidelobe suppression[J].IEEE Trans.on Aerospace and Electronic,2011, 47(4): 2473-2489.

[23] XU J, XIA X G, PENG S B, et al. Radar maneuvering target motion estimation based on generalized radon-Fourier transform[J].IEEE Trans.on Signal Processing, 2012, 60(12): 6190-6201.

[24] CHEN X L, GUAN J, LIU N B, et al. Maneuvering target detection via Radon-fractional Fourier transform-based long-time coherent integration[J].IEEE Trans.on Signal Processing, 2014, 62(4): 939-953.

[25] YU J, XU J, PENG Y N, et al. Radon-Fourier transform for radar target detection (III): optimality and fast implementations[J].IEEE Trans.on Aerospace and Electronic Systems, 2012, 48(2):991-1004.

[26] QIAN L C, XU J, SUN W F, et al. Efficient approach of generalized RFT based on PSO[C]∥Proc.of the 12th IEEE International Conference on Computer and Information Technology, 2013:511-516.

[27] QIAN L C, XU J, XIA X G, et al. Wideband-scaled Radon-Fourier transform for high-speed radar target detection[J]. IET Radar Sonar & Navigation, 2014, 8(5):501-512.

[28] QIAN L C, XU J, XIA X G, et al. Fast implementation of generalised Radon-Fourier transform for manoeuvring radar target detection[J]. Electronics Letters, 2012, 48(22):1427-1428.

[29] 吳兆平,符渭波,鄭紀彬,等.基于快速Radon-Fourier變換的雷達高速目標檢測[J].電子與信息學報,2012,34(8):1871-1886.

WU Z P, FU W B, ZHENG J B, et al. High speed radar target detection based on fast radon-Fourier transform[J].Journal of Electronics and Information Technology，2012, 34(8):1871-1886.

[30] 何友,關鍵,孟祥偉. 雷達自動檢測和CFAR處理方法綜述[J]. 系統工程與電子技術,2001, 23(1) :9-14.

HE Y, GUAN J, MENG X W. Survey of automatic radar detection and CFAR processing[J].Systems Engineering and Electronics, 2001, 23(1):9-14.

[31] 張軍,高貴,周蝶飛,等. SAR圖像機動目標檢測的兩種CFAR算法對比研究[J].信號處理,2008, 24(1): 78-82.

ZHANG J, GAO G, ZHOU D F, et al. Comparison on two CFAR algorithms of vehicle target detection in SAR images[J].Signal Processing，2008, 24(1): 78-82.