食餌庇護所對斑塊環境下Leslie-Gower捕食系統的影響

劉志廣

河南大學應用數學研究所數學與統計學院, 開封 475004

捕食是許多生態系統常見而又非常重要的種間作用關系。數學模型是理解和分析捕食者-食餌系統動態行為的一個重要且有效的工具,這其中最早也最著名的是Lotka-Volterra 模型[1]。這個模型假設捕食者對食餌的捕食效率(即功能反應)隨食餌種群密度的增加而成直線增加,但是實驗數據表明這個假設對很多種群不太合理[2]。根據物種類型和它們所處的環境,Holling提出3種不同類型的功能反應[3]。這些功能反應函數都假設捕食者的捕食效率只依賴食餌的數量,因此被稱為食餌依賴的功能反應。但越來越多的研究發現,有些物種捕食者的捕食效率除了受到食餌數量的影響,還會受到捕食者數量的影響,因此提出各種捕食者依賴的功能反應函數,例如率依賴[4]和捕食者間相互干擾[5-6]的功能反應函數。

另一類有趣的捕食者-食餌模型是考慮捕食者的增長函數與捕食函數不同。假設捕食者的增長項依賴捕食者和食餌數量的比值,這就是所謂的Leslie-Gower捕食者-食餌模型[7]。通過數值模擬[8]或嚴格的數學證明[9-10],可以知道這個系統唯一的正平衡點是全局穩定的。基于Leslie-Gower 框架,很多更加實際的具體因素被引入到這個模型或者其變種形式中,如其他形式的功能反應[11-12]、擴散[13]、時滯效應[14]、收獲效應[15]、Allee效應[16]和庇護所效應[17]等。

庇護所對捕食者-食餌系統的影響是數學生態學和理論生態學領域備受關注的課題。大部分研究關注食餌庇護所對系統穩定性的影響。研究表明,食餌庇護所可以穩定共存平衡點且防止食餌種群滅絕[18]。也有一些研究揭示在一定條件下可以破壞共存平衡點的穩定性[19]。另一方面,時間和空間庇護所對雜食系統物種共存的影響也越來越受關注[20-22]。以往研究大多利用基于Lotka-Volterra框架的捕食模型。研究方法往往通過修改功能反應函數來隱含的考慮食餌庇護所效應。環境異質性可以為食餌種群提供空間庇護所。斑塊環境下的種群相互作用模型是研究環境異質性的一個有效方法[23-26]。此模型由兩部分組成,一部分用于描述局部的物種相互作用,另一部分用于描述斑塊間的遷移。受此啟發,本研究提出一個兩斑塊環境的Leslie-Gower模型。其中一個斑塊表示開放的生境,另一個斑塊表示食餌的庇護所,從而就可以顯式地研究食餌庇護所的影響。基于此,本研究重點關注食餌庇護所對系統穩定性和捕食者食餌密度變化的影響。

1 捕食者-食餌的完全模型

假設有兩個斑塊,斑塊 1 上面生活著捕食者和食餌。x1(t)和y(t)表示在斑塊1上t時刻的食餌和捕食者的種群密度,可以用以下微分方程來描述：

(1)

這就是所謂的Leslie-Gower捕食者-食餌模型[7- 11]。此模型假設捕食者的環境容納量與食餌數量成比例。它強調捕食者和食餌的增長率都存在一個上限的實際情況,而這是Lotka-Volterra模型沒有注意到的[10]。這個上限只有在適合的條件下才能達到：對于捕食者來說,是在單位捕食者占有的食餌數量最大時；對于食餌來說,是在單位食餌占有的捕食者最少時。其中,r1,a1,b1,r2和a2是模型參數,都假設為正值。這些參數的生物學意義為：r1表示斑塊1上食餌的增長率,b1表示斑塊1上食餌的種內競爭強度,a1是最大捕食率,r2表示斑塊1捕食者的增長率,a2和a1有類似的意義。

另外,假設斑塊2為庇護所斑塊,只有食餌才可以遷移到上面,而捕食者不能遷移到上面。且假設斑塊2上面食餌的增長率為負,這是考慮到庇護所斑塊上面缺少資源和尋找配偶的機會[27]。假設遷移和生物相互作用發生在兩個不同的時間尺度上。遷移發生在快時間尺度,而種群的增長、死亡和捕食發生在慢時間尺度。本研究僅考慮非密度依賴的遷移方式。根據以上假設,可以建立一個顯式含有庇護所的兩斑塊捕食者-食餌模型如下：

(2)

式中,參數ε是一個非常小且無量綱的正數,它表示快慢時間尺度的比率。τ是快時間尺度。參數β表示食餌從斑塊1到斑塊2的遷移率,α的意義相反。參數d表示斑塊2上食餌的增長率,d>0表示在庇護所斑塊上食餌只能死亡。

2 綜合模型

基于已有的理論[23],可以將以上的完全系統簡化成只有兩個變量的綜合模型。這個方法的思想就是當有快慢兩個時間尺度的時候,認為在慢時間尺度系統的每一個時刻,快時間尺度系統都處于平衡態。因此可以將快時間尺度系統的平衡點代入到慢時間尺度的系統中,從而得到簡化的綜合系統。具體操作的方法是：第一步,忽略方程的慢時間尺度部分,從而研究在快時間尺度下的遷移模型。先來計算快時間尺度系統的平衡點。選取兩斑塊上物種的總密度作為綜合變量,即

x1(τ)+x2(τ)=x(τ),y(τ)=y(τ)

(3)

在快時間尺度上,x(τ)和y(τ)是常數。遷移可以改變兩個斑塊上食餌的比例,但不能改變它們的總密度。對方程(2),令ε=0,快的時間系統的平衡點為

(4)

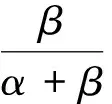
(I) 把模型(2)的前兩個方程相加,得到

(5)

(6)

式中t=ετ是慢時間尺度。

3 綜合模型正平衡點的穩定性

通過簡單計算,可以得到系統(6)唯一的內部平衡點：

(7)

(8)

因此,關于內部平衡點穩定性的主要結果表述如下：

證明：首先構造李雅普諾夫函數：

(9)

顯然,V(x,y)當x>0,y>0是有定義且連續。這個函數滿足：

(10)

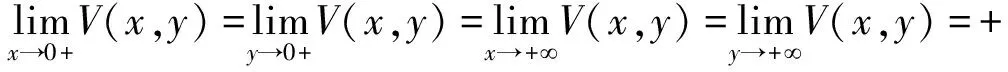
(11)

沿著系統(6)的解,計算V(x,y)的導數,并結合等式(8),得到

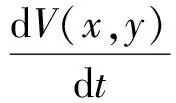
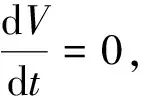
4 食餌庇護所的影響

4.1 食餌庇護所對捕食者密度的影響

(12)

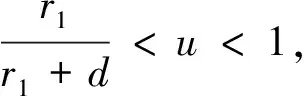
4.2 食餌庇護所對食餌密度的影響

改寫x*的表達式為如下形式:

(13)

通過計算x*關于u的導數：

(14)

5 結果與討論

在空間生態學的研究中,常見的數學模型可分為反應擴散方程、基于個體模型、集合種群模型、斑塊模型和網格模型[24]。網格模型常用于考慮空間結構和局部擴散對系統時空動態的影響。而斑塊模型常用于研究空間異質性和全局擴散對生態系統時空動態的影響。本研究就是利用斑塊模型來考慮庇護所斑塊和普通斑塊間的異質性對種群動態影響的。另外以往關于斑塊環境下捕食系統的研究大多假設遷移和局域相互作用發生在同一時間尺度,很少研究假設遷移發生在快時間尺度[25-26]。但很多現實情況是遷移和種群的增長、死亡及捕食發生在不同的時間尺度。比如,在水生環境下,浮游動物每天都表現出一種垂直遷移。兩個主要因子可以解釋這種現象：光和食物。在白天,光線增加了被魚類捕食的風險,這導致很多物種向下遷移到光線暗的地方從而減少捕食風險。晚上,這些物種在向上遷移去消費那些白天生產出的浮游植物[26]。在這種情況下,遷移相對于種群的增長、死亡和捕食來說是快時間尺度的。因為遷移每天都發生,而種群的增長、死亡和捕食發生在星期或者月的時間尺度上的。因此,假設遷移和種群過程不在同一個時間尺度往往更符合實際[23,25- 27]。另外,兩個時間尺度的好處在于可以利用奇異攝動理論將系統簡化[25],這樣數學上更方便分析。否則,包括兩個斑塊和遷移的模型非常復雜,很難得到一般的分析結果。

大部分關于空間庇護所對捕食系統動態影響的研究都基于Lotka-Volterra模型框架,有的研究采用隱含空間庇護所的模型[19],有的研究采用顯式含有空間庇護所的模型[27]。本研究基于Leslie-Gower捕食模型系統,而基于這個模型揭示食餌庇護所對系統動態的研究相對較少。因此本研究對全面認識和理解庇護所對不同類型生態系統動態的影響是非常有幫助的。最近,也有研究基于Leslie-Gower捕食系統,采用空間隱含的方法研究食餌庇護所對系統動態的影響[17]。研究揭示食餌庇護所對系統的續存沒有影響,但是增加了食餌平衡密度；在一定條件下,捕食者平衡密度與庇護所的數量呈現單峰曲線。與之不同,本研究采用顯式含有空間庇護所的方法,這樣更能體現空間及空間異質性所起到的作用。研究表明捕食者的平衡種群密度隨著躲進庇護所食餌數量增加而降低。這是因為被保護的食餌數量越多,捕食者的食物就越少,當然數量會越低。研究還發現在一定條件下,隨著躲進庇護所食餌數量的增加,食餌的平衡密度先增加后降低。這是因為我們假設庇護所上食餌不能生存。當躲進庇護所食餌數量比較小時,庇護所的保護作用大于捕食效應,所以食餌數量增加。但當被保護的食餌數量達到一定程度時,因庇護所上沒有食物，此時庇護所對躲在它上面的食餌的不利影響大于保護作用，因此食餌數量下降。這也就是說食餌種群存在一種利用庇護所的最佳策略。不能一味的躲進庇護所里面不出來,這實質上是捕食和庇護作用的權衡。顯式含有和隱含空間庇護所的數學模型所得結論不一致,這意味著在研究庇護所對捕食系統種群動態影響時,空間結構可能起著重要作用。到底哪種理論預測的結果更合理,還需結合以后的實驗工作來檢驗。

本研究假設斑塊間食餌的遷移是一種非密度依賴的方式。它代表的是一種逃逸行為,但這里給出的是被動的擴散而已,并沒有體現出隨捕食壓力加重的逃逸行為。假設食餌遷移是一種密度依賴的方式會更加合理。比如假設食餌的遷移率依賴所在斑塊的捕食者密度[25]、食餌密度[23]或者同時依賴于捕食者和食餌密度[26]。另外,本研究為了分析方便,假設只有兩個空間斑塊,擴展到多斑塊的情形也是值得思考的問題。此時,庇護所的空間位置、大小及空間結構對系統動態行為都會有影響[28]。

參考文獻(References):

[1] Lotka A J. Elements of Physical Biology. Baltimore: Williams and Wilkins Co., Inc., 1924.

[2] Begon M, Townsend C R, Harper J L. Ecology: From Individuals to Ecosystems. 4th ed. Oxford: Blackwell Publishing, 2005.

[3] Holling C S. Some characteristics of simple types of predation and parasitism. The Canadian Entomologist, 1959, 91(7): 385- 398.

[4] Arditi R, Ginzburg L R. Coupling in predator-prey dynamics: ratio-dependence. Journal of Theoretical Biology, 1989, 139(3): 311- 326.

[5] Beddington J R. Mutual interference between parasites or predators and its effect on searching efficiency. Journal of Animal Ecology, 1975, 44(1): 331- 340.

[6] DeAngelis D L, Goldstein R A, O′Neill R V. A model for tropic interaction. Ecology, 1975, 56(4): 881- 892.

[7] Leslie P H, Gower J C. The properties of a stochastic model for the predator-prey type of interaction between two species. Biometrika, 1960, 47(3/4): 219- 234.

[8] Pielou EC. Mathematical Ecology. New York: John Wiley & Sons, 1977.

[9] Hsu SB, Huang TW. Global stability for a class of predator-prey systems. SIAM Journal on Applied Mathematics, 1995, 55(3): 763- 783.

[10] Korobeinikov A. A Lyapunov function for Leslie-Gower predator-prey models. Applied Mathematics Letters, 2001, 14(6): 697- 699.

[11] Aziz-Alaoui M A, Okiye M D. Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling-type II schemes. Applied Mathematics Letters, 2003, 16(7): 1069- 1075.

[12] Huang J C, Ruan S G, Song J. Bifurcations in a predator-prey system of Leslie type with generalized Holling type III functional response. Journal of Differential Equations, 2014, 257(6): 1721- 1752.

[13] Yang W S. Global asymptotical stability and persistent property for a diffusive predator-prey system with modified Leslie-Gower functional response. Nonlinear Analysis: Real World Applications, 2013, 14(3): 1323- 1330.

[14] Nindjin A F, Aziz-Alaoui M A, Cadivel M. Analysis of a predator-prey model with modified Leslie-Gower and Holling-type II schemes with time delay. Nonlinear Analysis: Real World Applications, 2006, 7(5): 1104- 1118.

[15] Gupta RP, Chandra P. Bifurcation analysis of modified Leslie-Gower predator-prey model with Michaelis-Menten type prey harvesting. Journal of Mathematical Analysis and Applications, 2013, 398(1): 278- 295.

[16] Aguirre P, González-Olivares E, Sáez E. Three limit cycles in a Leslie-Gower predator-prey model with additive Allee effect. SIAM Journal on Applied Mathematics, 2009, 69(5): 1244- 1262.

[17] Chen F D, Chen L J, Xie X D. On a Leslie-Gower predator-prey model incorporating a prey refuge. Nonlinear Analysis: Real World Applications, 2009, 10(5): 2905- 2908.

[18] González-Olivares E, Ramos-Jiliberto R. Dynamic consequences of prey refuges in a simple model system: more prey, fewer predators and enhanced stability. Ecological Modelling, 2003, 166(1/2): 135- 146.

[19] Ma Z H, Li W L, Zhao Y, Wang W T, Zhang H, Li Z Z. Effects of prey refuges on a predator-prey model with a class of functional responses: the role of refuges. Mathematical Biosciences, 2009, 218(2): 73- 79.

[20] Finke D L, Denno R F. Spatial refuge from intraguild predation: implications for prey suppression and trophic cascades. Oecologia, 2006, 149(2): 265- 275.

[21] Amarasekare P. Coexistence of intraguild predators and prey in resource-rich environments. Ecology, 2008, 89(10): 2786- 2797.

[22] Liu Z G, Zhang F P. Species coexistence of communities with intraguild predation: the role of refuges used by the resource and the intraguild prey. Biosystems, 2003, 114(1): 25- 30.

[23] Michalski J, Poggiale JC, Arditi R, Auger PM. Macroscopic dynamic effects of migrations in patchy predator-prey systems. Journal of Theoretical Biology, 1997, 185(4): 459- 474.

[24] Briggs C J, Hoopes M F. Stabilizing effects in spatial parasitoid-host and predator-prey models: a review. Theoretical Population Biology, 2004, 65(3): 299- 315.

[25] El Abdllaoui A, Auger P, Kooi B W, de laParra R B, Mchich R. Effects of density-dependent migrations on stability of a two-patch predator-prey model. Mathematical Biosciences, 2007, 210(1): 335- 354.

[26] Mchich R, Auger P, Poggiale JC. Effect of predator density dependent dispersal of prey on stability of a predator-prey system. Mathematical Biosciences, 2007, 206(2): 343- 356.

[27] Ma Z H, Wang S F, Li W D, Li Z Z. The effect of prey refuge in a patchy predator-prey system. Mathematical Biosciences, 2013, 243(1): 126- 130.

[28] Mistro D C, Rodrigues L A D, Varriale M C. The role of spatial refuges in coupled map lattice model for host-parasitoid systems. Bulletin of Mathematical Biology, 2009, 71(8): 1934- 1953.