基于改進多層次灰色評價法的項目組合評價研究

董　欣　白思俊　劉海斌　郭云濤

(西北工業大學 管理學院，陜西 西安　710129)

0　引言

多層次灰色評價法是一種從評價等級的模糊性、不明確性出發，應用于對象復雜、層次多且不易量化的系統的評價方法，被廣泛應用于社會、經濟系統的評價，比如汪俠等將其用于對旅游者感知的綜合評價，蘇菊寧等研究了物流外包中的物流合作伙伴評價選擇問題，任宏等對建筑施工企業信息化能力進行了評價。項目組合的評價信息不僅分散而且具有模糊性，評價結果容易受到人為因素的影響。因此，多層次灰色評價法同樣適用于對項目組合的評價。郭鵬等利用灰色多層次綜合評價法對棕地再開發項目進行評價，計算各開發方案間的灰色關聯系數以構建灰色評價矩陣，提高了評價結果的準確性；王家遠等基于可持續發展的視角構建了住宅建設項目的綜合評價指標體系，運用多層次灰色評價法建立了綜合評價模型。但是，現有的研究并沒有指出白化權函數存在的集中趨勢，忽略了集中趨勢會使得綜合評價值之間的差異減少，不利于領導者做出正確的選擇。本文將多層次灰色評價法引入項目組合評價問題中，并針對多層次灰色評價法的不足進行改進，提出了修正函數，以減少白化權函數的集中趨勢，為項目組合評價提供一種新的思路，幫助企業的決策者更好地做出項目組合的選擇。

1　多層次灰色評價法的不足及改進

1.1　多層次灰色評價法的不足

傳統的多層次灰色評價法的不足之處在于白化權函數存在集中趨勢，導致綜合評價值之間的差異被弱化，不能滿足項目組合評價的需求。這里用實際例子加以說明。

簡化處理：對于項目組合方案，把指標體系簡化為一個指標V，其權重W=1；只有一個專家為評價指標打分，分值為x；經過白化權函數處理后的綜合評價值為Z，稱為實際值。

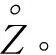
1.1.1實例的引入

將評價指標劃分4個等級，并分別賦值1、2、3、4分。對于項目組合方案，設評價專家的打分值為xs。相應設置4個評價灰類，序號為e(e=1,2,3,4)。設評價灰類的灰數為?1，?2，?3，?4，其對應的白化權函數為f1，f2，f3，f4。對4個評價灰類等級賦值1、2、3、4，得到評價等級值化向量G=(1，2，3，4)。

以一組典型的評價灰類為例，其白化權函數的解析式如下：

設方案S的綜合評價值為Zs，計算公式為

Zs=W·Rs·GT=

(1)

式中：

W——評價指標V的權重向量；

GT——評價等級值化向量的轉置矩陣；

Rs——方案S的灰色評價權向量。

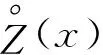
圖1　綜合評價值的集中趨勢

對兩個函數圖像比較分析我們發現，兩線相交于O點(3.179，3.179)。在O點左側區域，實際值大于參考值，x越小二者偏差越大；在O點右側區域，實際值小于參考值，x越大二者偏差也越大。與灰色的直線相比，黑色曲線的斜率更小，這說明綜合評價值的實際值趨于集中，數值之間的差異性被弱化。由于各評價灰類在中間灰色區域的疊加，導致中間等級的灰色評價權高于兩端區域的評價權。最終的結果是，綜合評價值向中間靠攏，產生“集中效應”。這種“集中效應”弱化了評價結果之間的差異，令決策者難以做出選擇和判斷。

1.1.2集中趨勢的量化

首先，明確Zs(x)的實際應用區間為[1，4]。可看出綜合評價值集中程度是與偏差程度呈正相關的，所以可以用實際值與參考值的偏差間接地反映實際值的集中程度。設偏差函數Ds(x)( Deviation)，它表示綜合評價值的實際值偏離參考值的程度，計算公式如下：

(2)

1.2　修正函數的提出及檢驗

1.2.1修正函數的提出

為了減弱綜合評價值的實際值的集中趨勢，對實際值函數Zs(x)做整體的旋轉變換，調整其斜率以接近參考值函數。由于Zs(x)的函數圖像是曲線，旋轉變換的計算過程較復雜，故選用一種簡化的方法間接得到一個近似結果。旋轉變換的具體操作步驟如下：

1.運用EXCEL軟件對區間[1，4]上的Zs(x)曲線做線性回歸，得到線性回歸方程：

y=0.502 7x+1.615 8 (1≤x≤4)

圖2　Zs(x)的線性回歸

2.求回歸線段的中點坐標：取區間[1，4]的中點x=2.5，代入線性回歸方程得y=2.8763，所以中點坐標為(2.5,2.8763)；

3.以中點為不動點對回歸線段做旋轉變換：設中點(2.5,2.8763)為不動點，對回歸直線進行旋轉，使其斜率為1，得直線y′=x+0.3763，變換方程如下：

(3)

4.將變換方程應用于Zs(x)，得到變換后的曲線Zs′(x)：

曲線Zs′(x)如圖3的灰色曲線所示：

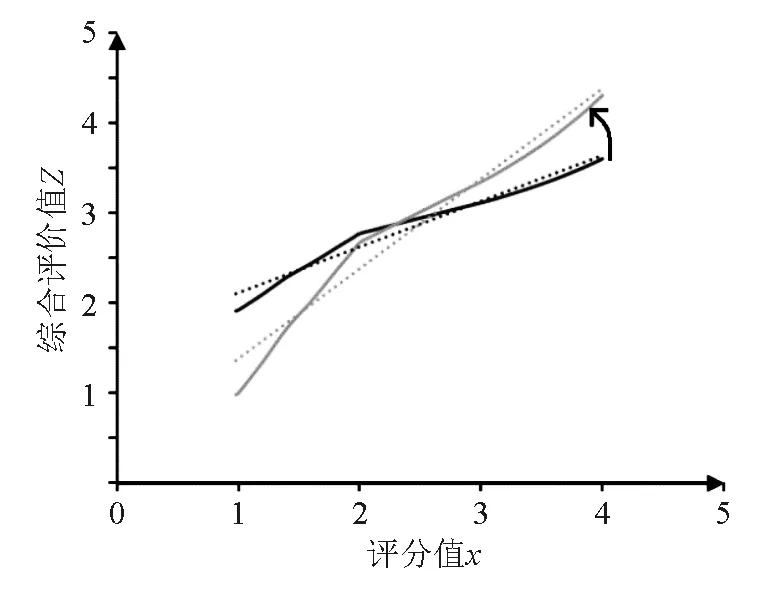
圖3　Zs(x)的修正變換

5.定義修正函數Cs(x)(Correction)：

對于具體的x0，其對應的修正系數為cs(x0)。在求出各綜合評價值的實際值后，再乘以相應的修正系數，即可增加各綜合評價值的離散程度，減少綜合評價值的集中趨勢。

1.2.2白化權函數的檢驗

選取統計學的兩個基本概念——期望值、方差，來描述偏差系數的平均大小和離散程度，定義平均偏差系數和偏差系數方差。由于偏差系數有正負之分，取偏差系數的絕對值進行計算。設白化權函數的實際應用區間為[a,b]，取a=min (g1，g2，L，gE)，b=max (g1，g2，L，gE)，即評分的最小值和最大值。

(5)

設偏差系數d在區間[a,b]上的概率分布函數P(x)為

(6)

對于某個具體的x值，它所對應的偏差系數為p(x)。

定義偏差系數方差σ2，表示偏差系數在實際應用區間內的離散程度：

(7)

2　項目組合評價的多層次灰色評價步驟

2.1　評分等級標準和評價灰類的確定

將評價指標的評分等級劃分為4級，分別賦值1，2，3，4分。當評價指標介于兩相鄰等級之間時，則賦值1.5，2.5或3.5。

設定4個評價灰類，序號為e(e=1,2,3,4)，分別對應于“差”“中”“良”“優”。各評價灰類的灰數為?1，?2，?3，?4，對應的白化權函數為f1,f2,f3,f4。最后對評價灰類進行賦值，得到評價灰類等級值化向量G=(1,2,3,4)。在這種情況下，將實際值函數修改為：

(8)

2.2　評價指標的賦權

本文從現有的國內外文獻中總結了基于平衡記分卡的戰略評價指標，采用德爾菲法來實現關鍵指標向項目型指標的轉化，并且在指標體系中增加了“項目間的協同度”這一指標來衡量項目組合內部的關聯性，最終得到5個一級指標，14個二級指標(見表1)。

表1　項目組合評價指標體系

本文采用乘法合成法的組合賦權方式，設層次分析法所確定的指標權重為αi，熵值法確定的指標權重為βi，組合賦權法所得權重為wi。乘法合成法的計算公式如下：

(9)

因此，得到二級評價指標的權重向量W：

W=(ω11，ω12，ω21，ω22，ω31，ω32，ω33，ω41，ω42，ω43，ω44，ω51，ω52，ω53)

2.3　評價樣本矩陣

設有p個評價專家對項目組合進行評價，序號為k(k=1,2,L,p)。對于項目組合Pt，設第k個評價專家給評價指標Vij的打分值為xijk(i=1,2,3,4,5；j=1,2,L,ni；k=1,2,L,p)，xijk構成了項目組合Pt的評價樣本矩陣：

2.4　灰色評價權矩陣

(10)

(11)

2.5　名義修正系數矩陣

(12)

(13)

(14)

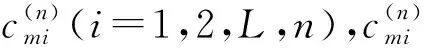
(15)

2.6　綜合評價值的計算

對于項目組合Pt，確定好灰色評價權矩陣R、二級評價指標權重向量W′、名義修正系數矩陣C(n)及評價等級值化向量G后，即可計算綜合評價值Z：

Z=W′·C(n)·R·GT

(16)

3　實例研究

3.1　企業背景介紹

X公司是我國一家以民用飛機設計、制造為主業的項目型企業，決策層決定采用項目組合的研發管理模式來實現企業的戰略目標。

經X公司高層領導和專家的決策，已經從8個備選項目(p1,p2,p3,p4,p5,p6,p7,p8)中選擇、制定了3個項目組合方案P1,P2,P3。其中，P1=(p1,p2,p4,p7)，P2=(p3,p4,p+,p7)，P3=(p2,p5,p6,p8)，選擇能最大化實現組織戰略目標的項目組合方案進行實施。

3.2　評價模型應用

(1)評價等級標準和評價灰類的確定。根據前文給出的評分等級標準，相應地確定4個評價灰類，灰類的序號為e(e=1,2,3,4)，給出灰類的灰數?e所對應的白化權函數分別為fe，如下所示：

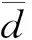
在實際應用區間[1，4]，實際值函數的解析式為

根據公式(2)求解偏差函數：

根據公式(5)求解平均偏差系數：

根據公式(6)先計算出偏差系數的分部概率函數P(x)，再根據公式(7)計算偏差系數方差：

(2)評價指標權重的確定。運用層次分析法得到判斷矩陣，計算各評價指標的相對重要度，并進行一致性檢驗。對于戰略目標V而言，一級評價指標Vi的相對重要度如表2所示。

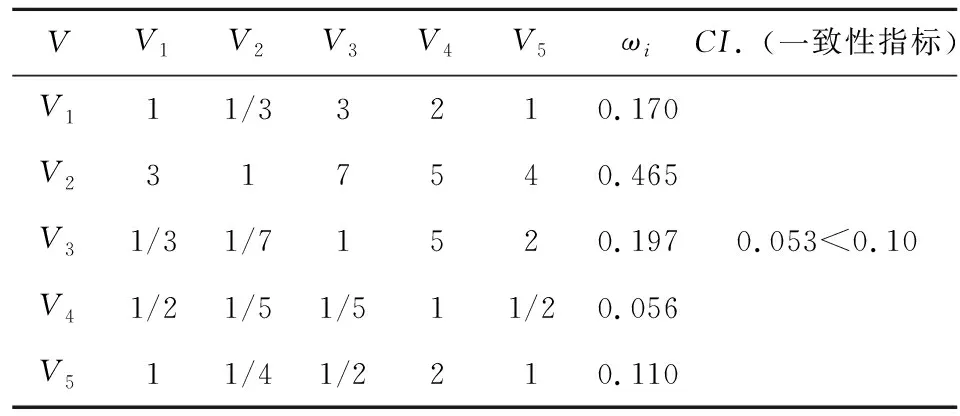
表2　判斷矩陣

運用層次分析法和熵值法分別得到各評價指標權重，根據公式(9)得到指標的組合權重如表3所示。

表3　組合賦權法得到的各指標相對重要度

最后，求各評價指標Vij相對戰略目標的權重，得到Vij的權重向量W：

W=(0.091;0.018;0.234;0.082;0.012;0.110;0.089;0.027;0.040;0.072;0.010;0.056;0.037;0.061)

(3)評價樣本矩陣。對于3個項目組合方案P1，P2，P3，邀請5位項目專家分別為指標打分，得到三個評價樣本矩陣X1,X2,X3：

(4)灰色評價權矩陣。得到評價樣本矩陣X1,X2,X3后，通過計算得到各個評價指標的灰色評價權向量，最后匯總構成灰色評價權矩陣R1,R2,R3：

(5)名義修正系數矩陣。根據修正函數的定義，代入白化權函數得到修正函數的解析式：

根據公式(12)、(14)計算出各項指標的名義修正系數，見表4。

表4　項目組合方案 P1，P2 ，P3的各名義修正系數

(6)綜合評價值

根據計算公式(16)，計算項目組合P1,P2,P3的綜合評價值，見表5。

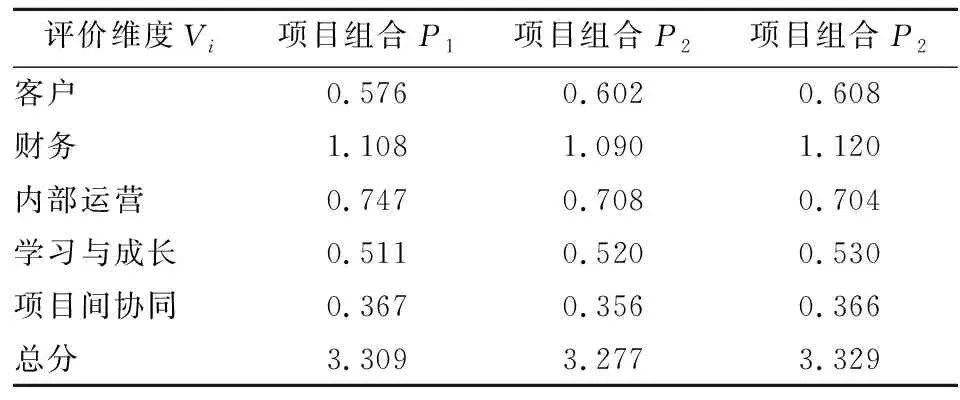
表5　各評價維度的評價值

3.3　評價結果比較

運用傳統的多層次灰色評價法計算綜合評價值，將所得到結果與改進方法得到的結果做比較，見表6。

表6　改進方法與傳統方法所得結果的比較

通過表6可以發現前者數據之間的差異大于后者，說明改進方法確實增加了綜合評價值之間的差異性，更有利于決策者作出分析和判斷。