硅壓阻式壓力傳感器的高精度補(bǔ)償算法及其實(shí)現(xiàn)
聶紹忠
(重慶四聯(lián)測控技術(shù)有限公司,重慶 401121)
0 引言
隨著科學(xué)技術(shù)的發(fā)展,各領(lǐng)域?qū)毫y量精度的要求越來越高。硅壓阻式壓力傳感器利用半導(dǎo)體材料的壓阻效應(yīng),基于惠斯頓電橋測量方式對壓力進(jìn)行測量,在動態(tài)性能、體積、價(jià)格等方面有較強(qiáng)優(yōu)勢,廣泛應(yīng)用于汽車、醫(yī)療、航空航天、環(huán)保等領(lǐng)域。但由于半導(dǎo)體材料對溫度的敏感性以及壓敏電阻制造工藝的局限性,硅壓阻式壓力傳感器普遍存在零點(diǎn)漂移、靈敏度漂移以及非線性等問題[1]。因此,需對該傳感器進(jìn)行有效補(bǔ)償,以提高輸出精度。目前,對于硅壓阻式壓力傳感器的補(bǔ)償主要有硬件補(bǔ)償和軟件補(bǔ)償兩大類。硬件補(bǔ)償對于靈敏度漂移的抑制效果并不理想,且高精度硬件電路復(fù)雜,調(diào)試較為困難,不利于工程應(yīng)用[2]。軟件補(bǔ)償以補(bǔ)償算法為主,其結(jié)合相應(yīng)的數(shù)學(xué)方法、計(jì)算機(jī)技術(shù),對上述問題進(jìn)行修正。實(shí)踐表明,軟件補(bǔ)償對于提高傳感器的輸出精度有很好的效果[3]。
常用的軟件補(bǔ)償算法有查表法、插值法、曲面擬合法等[4]。本文在回顧上述基本軟件補(bǔ)償算法的基礎(chǔ)上,設(shè)計(jì)了一種基于最小二乘法的曲面擬合補(bǔ)償算法,并在Visual Basic平臺上予以實(shí)現(xiàn);通過補(bǔ)償數(shù)據(jù)回代,對補(bǔ)償算法進(jìn)行了驗(yàn)證。
1 壓力傳感器軟件補(bǔ)償?shù)幕痉椒?/h2>1.1 數(shù)學(xué)模型
研究硅壓阻式壓力傳感器軟件補(bǔ)償,通常的做法是先建立一個(gè)補(bǔ)償?shù)臄?shù)學(xué)模型;然后采用一定的方法進(jìn)行標(biāo)定,分析標(biāo)定數(shù)據(jù)對數(shù)學(xué)模型的影響;最后求解數(shù)學(xué)模型,即一個(gè)反映傳感器輸入、輸出量關(guān)系的特征方程。在實(shí)際工況下,壓力傳感器感知外部壓力和環(huán)境溫度等,激勵(lì)內(nèi)部產(chǎn)生若干個(gè)電壓信號,并通過這些信號和特征方程計(jì)算出外部壓力[5]。對于雙參量體系下的硅壓阻式壓力傳感器,其特征方程為:
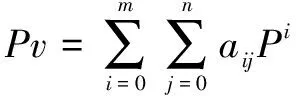
(1)
式中:Pv為標(biāo)定值;P為壓力輸出值;T為溫度輸出值;aij為多項(xiàng)式系數(shù)。
式(1)對應(yīng)一個(gè)多項(xiàng)式曲面。曲面表現(xiàn)能力與系數(shù)項(xiàng)a,自變量的最高次數(shù)m、n相關(guān)[6]。根據(jù)求解精度和復(fù)雜程度,間接或直接求解式(1)的方法主要有查表法、線性插值法和曲面擬合法。
1.2 查表法
早期的工程技術(shù)人員受限于求解方法和低速處理器,常常采用查表法。查表法擴(kuò)展了壓力傳感器的標(biāo)定方式,即對于可能的工作環(huán)境和工作區(qū)間內(nèi)的輸入、輸出進(jìn)行事先遍歷,并按一定順序?qū)⑦@些標(biāo)定值保存在二維或多維表格內(nèi)。壓力傳感器在實(shí)際工況下,其任意輸出均可在事先準(zhǔn)備好的表格中找到一個(gè)對應(yīng)的輸入。
查表法的關(guān)鍵是查找表的編制。對于單變量體系(P-Pv),應(yīng)繪制二維表格;對于多變量體系(同時(shí)考慮T),應(yīng)繪制三維或更高維度表格。
由此可知,查表法易于實(shí)現(xiàn),但工作量非常大,對存儲器空間要求高,不利于批量作業(yè)[7];標(biāo)定的過程非常漫長,如果減少標(biāo)定點(diǎn),則精度將隨之下降。
1.3 插值法
針對查表法所存在的問題,插值法是一個(gè)較好的解決辦法。插值法是一種重要的函數(shù)逼近方法。在工程實(shí)踐中,往往很難直接寫出函數(shù)f(x)表達(dá)式,只能通過采樣、試驗(yàn)的方法獲取函數(shù)的若干個(gè)值或?qū)?shù)值[8]。例如給定了函數(shù)f(x)在[a,b]上互異的(n+1)個(gè)點(diǎn)的值f(x)(i=0,1,…,n),插值法可根據(jù)這些值,尋求一個(gè)函數(shù)φ(x)去逼近f(x),且φ(x)在xi處與f(x)相等。
1.3.1 線性插值法
插值法中較常用的是線性插值法。給定f(x)在兩個(gè)互異的點(diǎn)(x0,y0)、(x1,y1)的值,用一個(gè)線性函數(shù)φ(x)=ax+b近似代替f(x),使f(x)的線性插值函數(shù)為:
該方法可應(yīng)用于單變量體系下的壓力傳感器。在單變量體系下,壓力傳感器的標(biāo)定值Pv與壓力輸出值P的傳感器特性曲線如圖1所示。
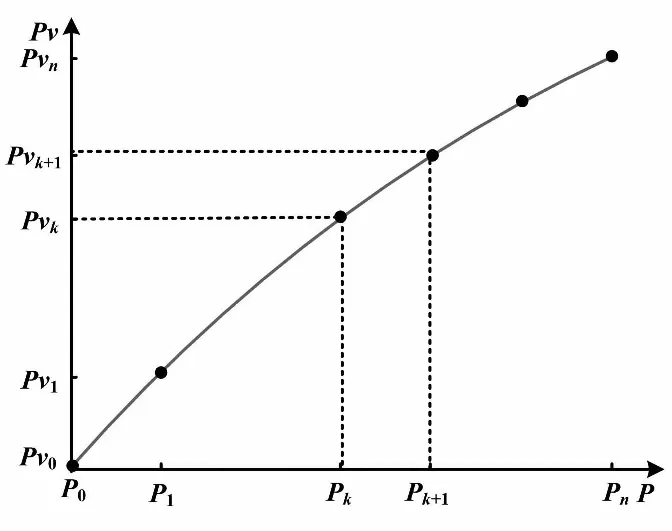
圖1 傳感器特性曲線Fig.1 The characteristic curve of sensor
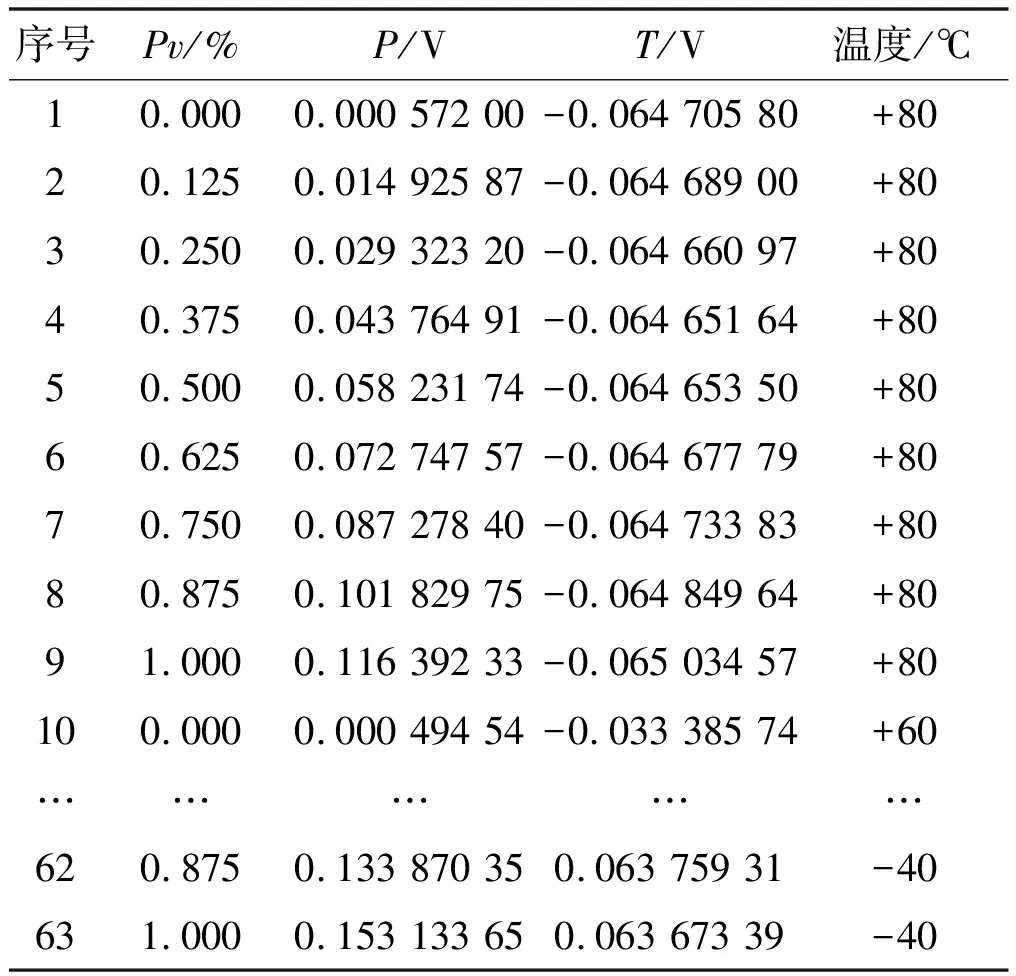
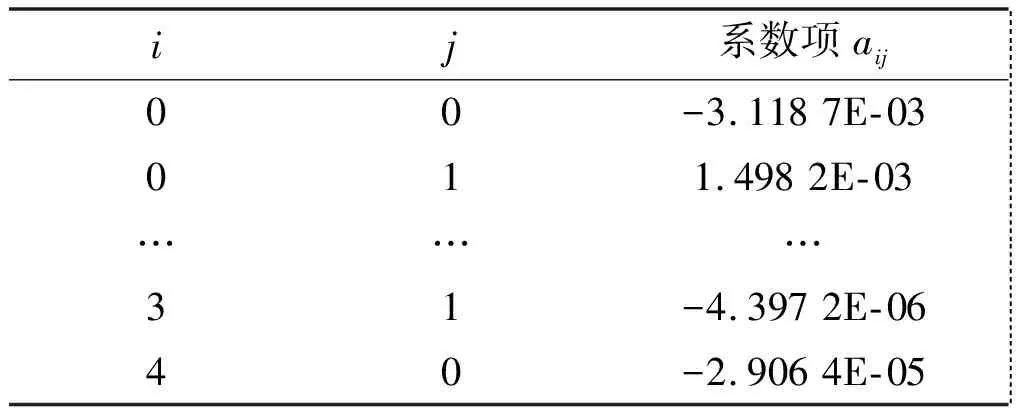
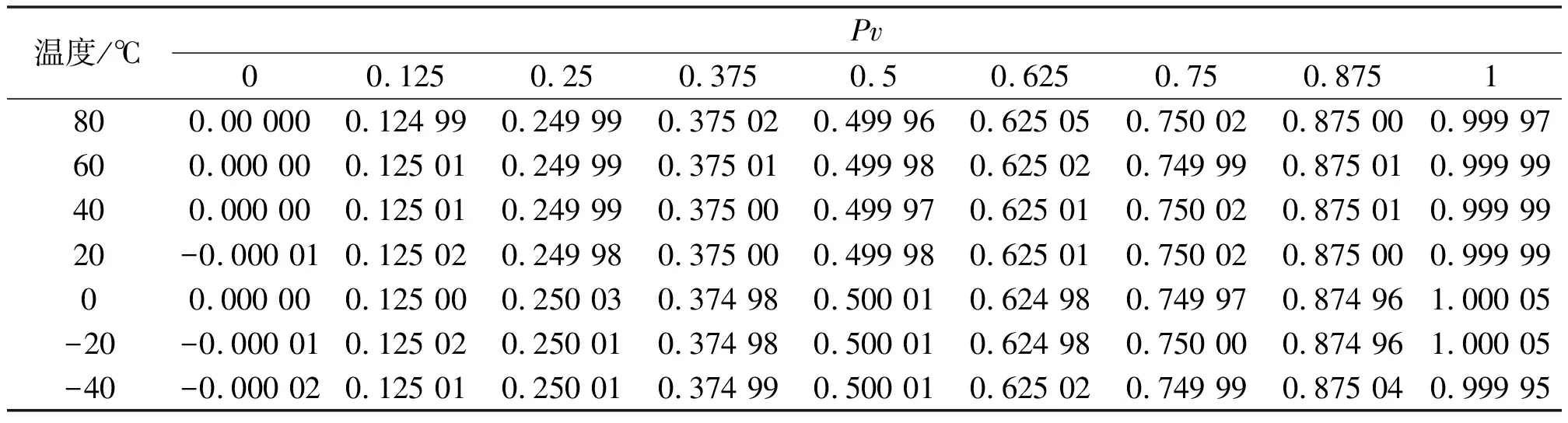
將P坐標(biāo)軸分成若干段,則對每個(gè)端點(diǎn)Pk,必有相應(yīng)的Pvk。把所有(Pk,Pvk)數(shù)據(jù)做成二維表格并固化入存儲器。在實(shí)際應(yīng)用中,壓力傳感器的壓力輸出值P必然在P坐標(biāo)軸某一段[Pk,Pk+1)上有定義,即Pk≤P (2) 線性插值法可以對單變量體系下的壓力傳感器進(jìn)行線性度補(bǔ)償,但無法對溫度變化造成的零點(diǎn)漂移和靈敏度漂移進(jìn)行溫度補(bǔ)償。此時(shí),可以采用雙線性插值的方法,引入溫度輸出值T。 1.3.2 雙線性插值 雙線性插值基本思路是在兩個(gè)變量方向分別進(jìn)行線性插值。故以雙變量體系下(P,T)的壓力傳感器為例,傳感器雙線性插值示意圖如圖2所示。圖2中:Qk(Pk,Tk,Pvk)、Qk+1(Pk+1,Tk+1,Pvk+1)為壓力傳感器在環(huán)境溫度為K時(shí)的標(biāo)定點(diǎn);Qj(Pj,Tj,Pvj)、Qj+1(Pj+1,Tj+1,Pvj+1)為壓力傳感器在環(huán)境溫度為J時(shí)的標(biāo)定點(diǎn);點(diǎn)O(Po,To,Pvo)為測試點(diǎn)(Po和To已知)。 圖2 傳感器雙線性插值示意圖Fig.2 The bilinear interpolation of sensor 插值公式推導(dǎo)的步驟如下。 ①沿Pk、Pk+1方向進(jìn)行線性插值: ②沿Pj、Pj+1方向進(jìn)行線性插值: ③一般情況下,Tk和Tk+1、Tj和Tj+1有著細(xì)微的差別。為了便于插值,可對Tk和Tk+1、Tj和Tj+1作均值處理,重新記為Tk、Tj;沿Tk、Tj方向進(jìn)行線性插值,最終完成一次雙線性插值,求得Pvo。 (3) 通過前述內(nèi)容,可以總結(jié)出對于多變量體系壓力傳感器的插值步驟為:當(dāng)前傳感器輸出獲取→根據(jù)傳感器輸出選取插值節(jié)點(diǎn)值→計(jì)算插值基函數(shù)值→用循環(huán)嵌套計(jì)算插值函數(shù)值。 雙線性插值法的優(yōu)勢在于可直接利用原始測試數(shù)據(jù),簡單直觀,計(jì)算量較小,具有較高精度,且適用于多變量場合。但其缺點(diǎn)也十分明顯,主要有如下幾點(diǎn)。 ①較查表法而言,雙線性插值法所需的存儲空間雖大大減少,但其仍處在一個(gè)非常高的水平。 ②由于雙線性插值法的特性,補(bǔ)償算法整體穩(wěn)定性較差[9]。在標(biāo)定過程中,如果出現(xiàn)了因壓力泄漏、溫度失準(zhǔn)、電路故障等情況造成的數(shù)據(jù)出錯(cuò)或失準(zhǔn),將會影響插值精度,且難以察覺。 ③在推導(dǎo)式(3)時(shí),采用了取均值的處理方式來保證插值的進(jìn)行。但這樣會引入系統(tǒng)誤差,最終影響插值精度。 最小二乘法是一項(xiàng)古老的數(shù)學(xué)優(yōu)化技術(shù),主要用于參數(shù)估計(jì)。它使數(shù)學(xué)模型在誤差平方和最小的情況下擬合試驗(yàn)數(shù)據(jù)。早在19世紀(jì)初,清楚、簡明地論述最小二乘法的文章便被發(fā)表。經(jīng)過200多年的不斷發(fā)展和完善,特別是進(jìn)入信息時(shí)代以來,借助計(jì)算機(jī)的強(qiáng)大運(yùn)算能力,最小二乘法在工程技術(shù)的各領(lǐng)域、各學(xué)科得到了廣泛的應(yīng)用。 對于形如式(1)的二元高次多項(xiàng)式方程,根據(jù)最小二乘法的思想,可定義函數(shù)Q為誤差平方和、φij(P,T)=PiTj、N為采樣數(shù)據(jù)樣本總數(shù),則: (4) 根據(jù)多元函數(shù)極值的必要條件: (Pp,Tp)]φkl(Pp,Tp)=0 (5) 展開后,式(5)表示為內(nèi)積形式: (6) 式中:0≤k≤m;0≤l≤n。 式(6)可表達(dá)為矩陣的形式,即正規(guī)方程[10]: (7) ①式(7)中,左邊內(nèi)積矩陣非奇異。 求解式(7),可得f(x)在函數(shù)類Φm中最小二乘逼近函數(shù)y(x)的表達(dá)式: 擬合余項(xiàng)為: 通過求解式(7)的線性方程組,確定曲面系數(shù)矩陣a,即式(1)的形式可確定。同時(shí),在式(7)的基礎(chǔ)上,可令若干個(gè)交叉項(xiàng)階次過高的aij為0,使式(1)變?yōu)槿表?xiàng)多項(xiàng)式,以避免過多的系數(shù)項(xiàng)。 算法軟件流程為:①讀取算法配置文件;②讀取采樣數(shù)據(jù)文件;③建立正規(guī)方程;④求解正規(guī)方程;⑤校驗(yàn)精度;⑥輸出結(jié)果。 通過第二節(jié)的討論,明確了補(bǔ)償算法的原理以及求解目標(biāo)函數(shù)的方法。接下來以Visual Basic為軟件平臺,設(shè)計(jì)、實(shí)現(xiàn)補(bǔ)償算法,驗(yàn)證算法的有效性,并將算法應(yīng)用于工程實(shí)踐中。 ①算法配置文件主要包括:各項(xiàng)aij的序列、溫度點(diǎn)數(shù)量、每個(gè)溫度點(diǎn)下壓力點(diǎn)數(shù)量;采樣數(shù)據(jù)文件記錄補(bǔ)償過程中各Pv、P、T的值。同時(shí),需對采樣數(shù)據(jù)進(jìn)行數(shù)據(jù)標(biāo)準(zhǔn)化處理,將數(shù)據(jù)控制在一定的范圍內(nèi),以提升后續(xù)計(jì)算速度。 ②正規(guī)方程利用相應(yīng)的內(nèi)積計(jì)算模塊,按照式(4)構(gòu)建。定義雙精度數(shù)據(jù)類型數(shù)組,存儲正規(guī)方程中各內(nèi)積構(gòu)成的元素。 ③正規(guī)方程的求解,實(shí)質(zhì)是線性方程組求解的問題。本算法采用逐次超松弛迭代法(successive over relaxation,SOR)求解正規(guī)方程。在迭代計(jì)算模塊中,構(gòu)建四個(gè)雙精度數(shù)據(jù)類型數(shù)組,分別存儲迭代初值、迭代值、加速項(xiàng)以及常速項(xiàng)。在迭代計(jì)算模塊中,需設(shè)置迭代次數(shù)上限。當(dāng)?shù)螖?shù)超過上限后仍無法滿足迭代精度,則迭代過程終止并報(bào)告錯(cuò)誤。 試驗(yàn)所選壓力傳感器的量程為0~40 MPa。在高低溫試驗(yàn)箱內(nèi)部,將壓力傳感器裝夾在與標(biāo)定壓力源連通的夾具上。在不同的溫度點(diǎn)下,利用標(biāo)準(zhǔn)壓力源(Fluke公司7350壓力控制器),對壓力傳感器輸入標(biāo)定壓力(從0%~100%量程取若干個(gè)Pv),讀取、記錄傳感器輸出的若干組Pv、P和T。 試驗(yàn)中,選取測試溫度點(diǎn)為-40 ℃、-20 ℃、0 ℃、+20 ℃、+40 ℃、+60 ℃、+80 ℃。在各溫度點(diǎn)分別施加9檔壓力(以滿量程的百分比形式表示),即0%、12.5%、25%、37.5%、50%、62.5%、75%、87.5%、100%。在每個(gè)“溫度點(diǎn)-輸入壓力”下讀取標(biāo)定壓力Pv、壓力傳感器電壓輸出值P、溫度傳感器電壓輸出值T,如表1所示。 表1 補(bǔ)償采樣數(shù)據(jù)Tab.1 Compensation sampling data 在利用算法軟件計(jì)算前,按照式(1)配置m=4、n=7,構(gòu)建缺項(xiàng)多項(xiàng)式,共21項(xiàng);7個(gè)溫度點(diǎn),每個(gè)溫度點(diǎn)下9個(gè)壓力點(diǎn);所有P、T采樣數(shù)據(jù)放大20倍作標(biāo)準(zhǔn)化處理;SOR迭代法ω=1.1,迭代精度Acc=10-8[11]。 配置完成后,算法軟件將自動開始計(jì)算,輸出多項(xiàng)式系數(shù)項(xiàng)如表2所示。 表2 多項(xiàng)式系數(shù)項(xiàng)Tab.2 Polynomial coefficient terms 將表1、表2數(shù)據(jù)代入式(1),得到如表3所示的回代壓力值。 表3 回代壓力值Tab.3 Back substituted pressures 本文利用最小二乘法的基本定義,將曲線擬合法轉(zhuǎn)化為多項(xiàng)式系數(shù)項(xiàng)可預(yù)置的曲面擬合法,提出了一種基于最小二乘法的曲面擬合補(bǔ)償算法。該補(bǔ)償算法可有效補(bǔ)償硅壓阻式壓力傳感器的零點(diǎn)、靈敏度和線性度,準(zhǔn)確地建立表達(dá)傳感器輸入-輸出關(guān)系的特征方程。試驗(yàn)結(jié)果表明,該補(bǔ)償算法對硅壓阻式壓力傳感器的補(bǔ)償效果十分明顯,極大地提高了該類傳感器在-40~+80 ℃范圍內(nèi)的輸出精度;同時(shí),該算法的設(shè)計(jì)和實(shí)現(xiàn)僅需利用較為基礎(chǔ)的編程語言,可操作性強(qiáng),有著良好的工程應(yīng)用價(jià)值。 參考文獻(xiàn): [1] 邱金.硅基壓阻式數(shù)字壓力傳感器的研究[D].沈陽:沈陽工業(yè)大學(xué),2009. [2] 劉曄,張璐,楊新偉,等.采用硬件神經(jīng)電路的壓力傳感器零點(diǎn)溫漂補(bǔ)償研究[J].西安交通大學(xué)學(xué)報(bào),2010,44(8):10-14. [3] XU D.A temperature compensation algorithm of piezoresistive pressure sensor and software implementation[C]// IEEE International Conference on Mechatronics & Automation,2013:1738-1742. [4] 華振宇,徐大誠.硅壓阻式壓力傳感器誤差修正算法的FPGA實(shí)現(xiàn)[J].傳感器與微系統(tǒng),2017(2):101-103. [5] 何慎之.高精度MEMS硅差壓傳感器過載保護(hù)與溫度漂移補(bǔ)償研究[D].廣州:華南理工大學(xué),2015. [6] GUO J,CHANG X,Yue Q.Study on curved fitting model using GPS and leveling in local area[C]//Transactions of Nonferrous Metals Society of China,2005: 140-144. [7] 歐陽承曦.硅壓阻式壓力傳感器高精度溫度補(bǔ)償技術(shù)研究[D].成都:電子科技大學(xué),2015. [8] ZENG M,ZHANG Y,HUAN J.A new linear interpolation algorithm[C]//Proceedings of the 2016 International Conference on Computer Engineering,Information Science & Application Technology,2016: 163-170. [9] 董燕婷.微差壓變送器的研究與溫度補(bǔ)償實(shí)現(xiàn)[D].上海:上海交通大學(xué),2014. [10]秦寧.基于整體最小二乘面擬合及其在GPS高程擬合的研究應(yīng)用[D].成都:西南交通大學(xué),2015. [11]ZHANG C,XUE Z,LUO S.A convergence analysis of SOR iterative methods for linear systems with weak H-matrices[J].Open Mathematics,2016,14 (1):747-760.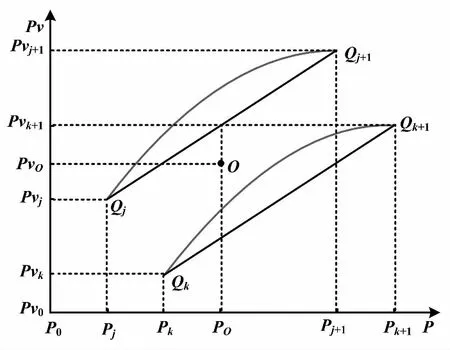
2 基于最小二乘法的曲面擬合補(bǔ)償算法
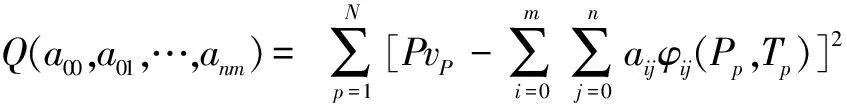
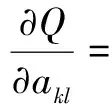
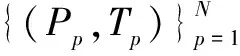
3 算法軟件設(shè)計(jì)與實(shí)現(xiàn)
4 試驗(yàn)結(jié)果與誤差分析
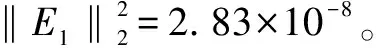
5 結(jié)束語

