例析多池相連電化學裝置的解題方法

莫麗瓊，王 霞

（云南師范大學 云南 昆明 650500）

1 引言

電化學知識是近幾年全國各省市高考題中的必考考點[1]，它是基于氧化還原反應、化學反應中的能量變化等知識的深度學習，電化學分為原電池與電解池兩大模塊，但考題中通常不單獨考察，而是多池相連綜合考察，因而要求學生具有扎實的基礎知識儲備與強大的邏輯思維體系。因此本文舉例分析常見的多池相連問題的題型特點和相應的解題方法談談自己的見解。

2 無外接電源型

2.1 建立認知角度

此類題型關鍵是確定原電池，判斷方法主要有：找裝置中最活潑金屬，其在裝置為原電池（即能自發(fā)進行氧化還原反應的電池），其余為電解池；在電極附近有可燃物通入的裝置是原電池，其余為電解池。

2.2 建立角度關聯(lián)

根據原電池的形成條件確定其正負極，較活潑金屬或可燃物做負極，另一極為正極。與原電池負極相連的是電解池的陰極，與正極相連的是陽極，串聯(lián)電池中陰陽電極交替出現(xiàn)。

2.3 建立思維模型

根據解題需要建立思維模型，正確書寫電極反應方程式，判斷電子轉移方向，陰陽離子移動方向等，緊抓相同時間內電極通過電子的物質的量相等這一橋梁來解答電化學中的定量計算。

例：如圖裝置甲池的總電極反應式為2CH3OH＋3O2＋4KOH===2K2CO3＋6H2O。下列敘述正確的是( )

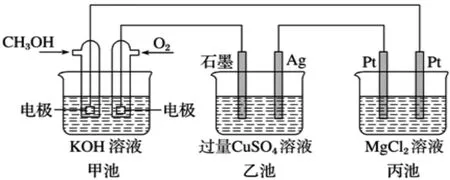
A.甲池是原電池，乙池是化學能轉化為電能的裝置

B.乙池中，Ag電極的電極反應式為Ag-e-=Ag+

C.反應一段時間后，若要使CuSO4溶液恢復到原濃度則向乙池中加入一定量Cu(OH)2固體

D.當甲池中消耗標準狀況下280mL O2，理論上丙池中最多產生固體1.45g

解析：甲池中有CH3OH通入做原電池，乙池和丙池為電解池，能量是電能轉化為化學能，A錯。甲池中負極為通入CH3OH的一極，正極為通入O2的一極，乙池中Ag作陰極，電極反應為Cu2+＋2e-===Cu，B錯。恢復原溶液的原則是電解了什么則加入什么，乙池中：2CuSO4＋應加入CuO或CuCO3，C錯。丙池中：當消耗標況下280mL O2，0.0125mol時，轉移e-0.05 mol，生成Mg(OH)20.025mol，質量為1.45g。

3 有外接電源型

（1）建立認知角度：針對有電源的此類題型，全部為電解池、電鍍池或精煉池等。（2）建立角度關聯(lián)：若已知電源的正負極，則與電源負極相連的是電解池的陰極，與正極相連的是陽極，根據串聯(lián)電池中電極交替出現(xiàn)原則順推其他電極；若未知電源的正負極，則需要根據某極發(fā)生的現(xiàn)象逆推電極（隱含著電子流向、陰陽離子移動方向等解題依據）。（3）建立思維模型：與無外接電源型類似

例：如圖裝置電解一段時間，當某極析出0.32gCu時，Ⅰ、Ⅱ、Ⅲ中溶液pH分別為(溶液足量，體積均為100mL且電解前后溶液體積變化忽略不計)( )

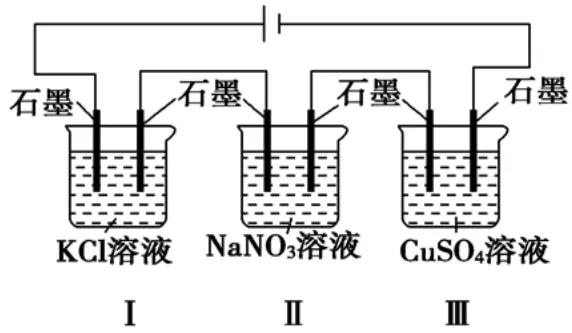
A．13、7、1 B．12、7、2

C．1、7、13 D．7、13、1

解析：Ⅰ、Ⅱ、Ⅲ均為電解池，Ⅰ中石墨（左）與電源正極相連為陽極，石墨（右）為陰極，Ⅱ、Ⅲ中依次交替。n(Cu)＝0.005mol，由Ⅲ中陰極的電極反應為Cu2+＋2e-===Cu可知轉移e-0.01mol，Ⅰ、Ⅱ、Ⅲ中電解方程式分別為當轉移e-0.01mol時，則Ⅰ中生成OH-0.01mol，c(OH-)＝0.1mol/L，pH＝13；Ⅱ電解水，溶液仍然呈中性，溶液的pH＝7；Ⅲ中生成0.01molH+，c(H+)＝0.1mol/L，pH＝1，故選A。

4 雙控型

此類題型是前面兩類的綜合運用，通過電建的斷開與閉合，從而改變認知角度。

例：有關下列裝置的敘述中正確的是（ ）

A.斷開K1，閉合K2后，甲、乙池能將化學能轉化為電能

B.斷開K1，閉合K2后，丙池中c(Cl-)減小

C.斷開K2，閉合K1后，乙池右邊C電極上的電極反應式為4OH--4e-===2H2O＋O2↑

D.斷開K2，閉合K1后，一段時間后甲、乙、丙三池中的陽極均被腐蝕了

解析：斷開K1，閉合K2后，整個裝置中為無外接電源型，由于鋅銀銅中鋅為最活潑金屬，故甲池是原電池，則乙、丙兩池為電解池，乙池是將電能轉化為化學能，A錯。甲池中Zn做負極，丙池中與Zn相連的Cu（右）電極為陰極，Cu（左）電極為陽極，Cu-2e-=Cu2+，金屬電極做陽極，參與電極反應，Cl-不放電，B錯。斷開K2，閉合K1后，三個池子均變成電解池，甲池中Zn與電源負極相連做陰極，則乙池中C（右）電極為陽極，4OH--4e-=2H2O＋O2↑，C正確；石墨是惰性電極，本身不參與電極反應，D錯。

解答電化學的相關題型，氧化還原反應是基礎，原電池與電解池的工作原理是關鍵，經分析發(fā)現(xiàn)，無論電化學以哪種題型出現(xiàn)，基礎知識都是考察的重點和核心，這就要求學生在強化基礎知識的同時，不斷減少迷思概念，形成一定的邏輯思維體系，構建解題模型，當遇到綜合性較強的題型時就能迎刃而解了。

[1] 李輝，徐文華．電化學電極反應式書寫“三步曲”[J].高中數理化.2015(5)：56-58.