基于時—頻包線的非平穩(wěn)地震動合成及其對結構非線性響應的影響

曲國巖 俞瑞芳

摘要： 地震動頻率非平穩(wěn)特性對結構的非線性響應有重要影響。引入具有統(tǒng)計參數(shù)的時-頻包線函數(shù)來近似模擬地震動頻率非平穩(wěn)特性，建立了以反應譜為目標的非平穩(wěn)地震動擬合方法。以天然地震動為種子，設計了4種時程擬合方案，得到了滿足相同目標譜的4組加速度時程，結果分析表明，（1）本文建立的地震動擬合方法，能夠很好地保留原始地震動的非平穩(wěn)特性和持續(xù)時間，且擬合精度較高；（2）基于實際地震動提取的時-頻包線函數(shù)，能夠較好地模擬地震動頻率的非平穩(wěn)特性；（3）基于統(tǒng)計參數(shù)定義的時-頻包線函數(shù)能夠近似模擬地震動頻率非平穩(wěn)特性，與真實地震動頻率隨時間的變化規(guī)律符合較好。以這4組地震加速度時程作為輸入，分別對層數(shù)為7層和15層的規(guī)則鋼筋混凝土框架結構進行三維非線性時程分析，結果表明，采用僅考慮強度非平穩(wěn)特性的地震輸入，存在低估規(guī)則鋼筋混凝土結構非線性響應的風險，因此在人工合成地震動中應該考慮其頻率的非平穩(wěn)特性，合理估計結構的非線性響應，保證結構設計的安全性。

關鍵詞： 隨機振動； 地震動； 結構非線性響應； 頻率非平穩(wěn)特性； 地震動合成

中圖分類號： O324； TU311.3文獻標志碼： A文章編號： 1004-4523（2018）02-0198-11

DOI：10.16385/j.cnki.issn.1004-4523.2018.02.002

引 言

實際地震動是一個非平穩(wěn)的隨機過程。工程中常用的強度包線函數(shù)，能夠反映地震動強度的非平穩(wěn)過程，即認為地震動經(jīng)歷一定長度的上升時間段，達到某一強度并保持平穩(wěn)持續(xù)一段時間，然后再緩慢衰減至地震動結束[1]。但強度包線并不能反映實際地震記錄中頻率隨時間變化的特性，即地震動的頻率非平穩(wěn)特性[2]。從結構響應的角度看，地震動的非平穩(wěn)特性可以理解成地震動能量在頻率和時間上的不均勻分布。不少研究表明，地震動的能量如果在頻率和時間上分布相對集中，那么它要比能量分布相對均勻的地震動對結構產(chǎn)生更為嚴重的破壞[3]。因此地震動頻率含量變化對結構的影響，特別是對結構非線性時程分析結果將產(chǎn)生不可忽視的影響[4-5]。分析近年來的研究成果，主要分為兩類，一類研究結果認為，結構進入非線性狀態(tài)時，結構頻率有降低的趨勢，實際地震動在持時后半段低頻分量較為豐富，則結構會因共振而產(chǎn)生更大的響應[6-7]，影響程度則與頻率的非平穩(wěn)程度有關[8]；另一類研究結果則認為，結構的最大反應通常發(fā)生在強震階段，而非地震動的后期，由于地震動后期幅值變小很多，即使低頻分量變得更顯著也不會引起更大的響應[9]。地震動頻率的非平穩(wěn)特性究竟對結構響應有多大的影響，學者們并沒有得出明確的結論。

因此，本文的研究目的主要有兩個，一是引入具有統(tǒng)計參數(shù)的時-頻包線函數(shù)，近似模擬地震動頻率非平穩(wěn)特性，建立能夠反映地震動頻率非平穩(wěn)特性的擬合方法，為結構地震響應分析提供合理的輸入；二是通過采用不同的擬合方法，控制地震輸入的頻譜特性，分析地震動非平穩(wěn)特性對結構非線性響應的影響。結果分析表明，本文建立的頻率非平穩(wěn)地震動的擬合方法能夠近似反映地震動的非平穩(wěn)特性；地震動頻率非平穩(wěn)特性對規(guī)則鋼筋混凝土結構的非線性響應有不可忽視的影響，僅考慮地震動的強度非平穩(wěn)特性，存在低估規(guī)則鋼筋混凝土結構非線性響應的風險。因此，在實際工程應用中，為了合理估計結構的非線性響應，保證結構設計的安全性，不應忽視地震動的頻率非平穩(wěn)特性。

1 基于時-頻包線函數(shù)的地震動合成方法1.1 非平穩(wěn)地震動合成的基本公式

為了能夠反映地震動頻率的非平穩(wěn)變化，本文采用以下隨機過程模型[10]，即y（t）=∫∞-∞B（t，ω）eiωtdF（ω）（1）式中 i=-1，B（t，ω）是一個確定的時-頻調(diào)制函數(shù)，表示了一個地震過程絕對幅值的包絡。若將B（t，ω）換成工程中常用的僅依賴于時間變化的強度包線函數(shù)[11-12]，則式（1）就僅能考慮地震動強度非平穩(wěn)特性。dF（ω）表示一個零均值，相互獨立的正交過程：E[dF（ω）]=0（2）

E[dF*（ω1）dF（ω2）]=δ（ω1-ω2）S（ω1）dω1dω2（3）式中 E[·]表示總體的平均值，δ（·）為狄拉克δ函數(shù)，*表示復共軛，S（ω）為dF（ω）的功率譜密度函數(shù)。

在地震工程中，時頻調(diào)制函數(shù)只有當它是實數(shù)、非負的時候才有意義，即B（t，ω）∈R， B（t，ω）≥0（4） 假設，對于給定的ωk，B（t，ω）有max[B（t，ωk）]=1（5）B（t，ωk）僅確定的是相應于頻率ωk的包絡線的形狀，而ωk處地震動的幅值則由功率譜密度函數(shù)S（ωk）來決定。因此，根據(jù)式（1），采用三角級數(shù)法生成人工地震動時程，即y（t）=∑nk=1B（t，ωk）2S（ωk）Δωcos（ωkt+k）（6）式中 Δω為頻率的增量，ωk為離散的頻率，k為[0，2π]間均勻分布的隨機相位。

很明顯，如果根據(jù)實際工程需要能夠合理地估計對應于不同頻率ωk的時頻包線函數(shù)B（t，ωk），式（6）的計算就會很簡單。

1.2 具有統(tǒng)計參數(shù)的時-頻包線函數(shù)B（t，ω）

近年來，能夠從時域和頻域聯(lián)合描述地震動強度和頻率非平穩(wěn)特性的瞬時譜得到了發(fā)展[13-14]。瞬時譜具有時間和頻率分辨能力，能更準確地反映地震動非平穩(wěn)特性，但是由于對時間和頻率的二元函數(shù)描述過于復雜，且影響模型參數(shù)的因素較多、統(tǒng)計性較差，使瞬時譜無法直接用于工程實踐。文獻[15]提出了用主頻率Fp來近似模擬地震動頻率隨時間的變化。Fp表示在一系列采樣時間點上，對應于時頻譜最大幅值的頻率值（如圖1所示），文獻[15]基于對NGA數(shù)據(jù)庫中10545條加速度記錄的時-頻分析，給出了不同震級、震中距及場地條件下計算Fp的統(tǒng)計參數(shù)，非常方便工程應用。主頻率計算公式[15]Fp（t）=f0+pe-stsin（ωt）（7） 第2期曲國巖，等： 基于時-頻包線的非平穩(wěn)地震動合成及其對結構非線性響應的影響振 動 工 程 學 報第31卷 式中 Fp表示的是在一系列采樣時間點上（t1，t2，…，tn），對應于小波譜的最大幅值的頻率值，即主頻率；參數(shù)f0，p，s，ω具有統(tǒng)計意義，決定了主頻率時變曲線的形狀。

圖1 主頻率的定義[15]

Fig.1 Definition of predominant frequencies[15]

對于一系列時間采樣點tk，時頻譜的變化可以用單峰函數(shù)來表示L（f，tk）=fFp（tk）e-f-Fp（tk）Fp（tk）（8）式中 f為頻率，F(xiàn)p（tk）為每個采樣時間點tk處的主頻率，如式（7）所示。

用E（t）表示地震動的幅值隨時間的變化過程，則地震動的時頻聯(lián)合分布可定義為WB（t，f）=E2（t）L（f，t） （9）因此對應于不同的采樣頻率fk處，時頻包線函數(shù)B（t，fk）可以通過正規(guī)化WB（t，f）得到，即

B（t，fk）=WB（t，fk）/max[WB（t，fk）]，

k=1，2，… （10）

如果選取二類場地、M[6.5，7.0）、R[40-60]的主頻參數(shù)，即：

Fp（t）=3.392+25e-0.008tsin（-0.004t）（11）

選擇雙指數(shù)函數(shù)模型描述地震動的強度變化，即E（t）=I0（e-αt-e-βt）（12）式中 α=0.08，β=0.085，I0=1。即可獲得地震動隨頻率變化的包線函數(shù)B（t，ω）。B（t，ω）在頻率分別為0.8，5.0，10 Hz的變化曲線如圖2所示。可以看出，頻率越小，低頻分量就變得越突出，也就是說，隨頻率變化的調(diào)制函數(shù)B（t，ω）符合地震動頻率隨時間的變化規(guī)律，能夠反映地震動頻率的變化特性。

圖2 具有統(tǒng)計參數(shù)的時-頻包線函數(shù)B（t，ω）

Fig.2 Frequency-dependent amplitude envelope function B（t，ω）1.3 提取實際地震動的時-頻包線函數(shù)B（t，ω）

基于實際地震動計算的瞬時譜適合于特定地震記錄的仿真再現(xiàn)。隨著時頻分析技術的發(fā)展，目前可以采用多種方法對實際地震進行時頻分析，例如時變功率譜（瞬時功率譜、漸進功率譜、物理譜）、ARMA模型、Wigner-Ville分布、小波變換和Hibert-Huang變換等[16-19]。

本文采用一維連續(xù)小波變換提取能反映實際頻譜特性的包線函數(shù)B（t，ω）。對于選定的小波函數(shù)ψa，b（t），將地震信號y（t）做連續(xù)小波變換，即可得到關于時間和尺度的小波系數(shù)

WS（a，b）=∫+∞-∞y（t）ψa，b（t）dt=

1a∫+∞-∞y（t）ψ（t-ba）dt （13）

式中 ψa，b（t）為小波函數(shù)ψa，b（t）的共軛函數(shù)，a為尺度因子，b為平移因子。

相應于尺度因子a的頻率Fa可以表示為Fa=Fcfsa（14）式中 Fc為小波基ψ（t）的中心頻率，有Fc=1，fs為加速度時程y（t）的采樣頻率。

對地震動y（t）進行一維連續(xù)小波變換，即得到強震記錄y（t）在小波函數(shù)上的分量，展開參數(shù)a和b，即可得到任意時刻、任意尺度的頻譜。將尺度換算成頻率，從而得到關于時間和頻率的小波譜WS（t，ω）。因此，式（6）中相應于不同ωk處的B（t，ωk）就可以通過規(guī)則化小波譜，即

B（t，ωk）=WS（t，ωk）/max[WS（t，ωk）]，

k=1，2，… （15）

式中 k為離散頻率的點數(shù)。圖3給出了Imperial Valley-06地震記錄的頻率為0.8，5.0，10 Hz的包線函數(shù)。與圖2給出的頻率變化曲線相比，該方法得到的包線函數(shù)隨時間變化呈現(xiàn)出不同的抖動狀態(tài)，而圖2中時頻包線函數(shù)過于光滑，因此，采用式（10）所示的包線函數(shù)進行地震動擬合時，會忽略了實際地震動的一些細小因素。

圖3 提取天然地震動不同頻率處的包線函數(shù)B（t，ω）

Fig.3 Frequency-dependent amplitude envelope function B（t，ω） at different frequencies of natural ground motion2 基于反應譜的頻率非平穩(wěn)地震動擬合 基于目標反應譜對初始地震動進行調(diào)節(jié)的目的是，使調(diào)整后的地震動在能夠真實反映實際地震動頻譜特性的同時，滿足對目標反應譜的擬合精度[20-21]。本文基于目標反應譜、地震動主頻率時變曲線，采用在時域疊加加速度脈沖響應函數(shù)的方法，并引入隨頻率變化的包線函數(shù)，建立了能夠實現(xiàn)多個目標的頻率非平穩(wěn)地震動的擬合方法。

在時域內(nèi)對初始地震動進行調(diào)整時，由于對時程的微小調(diào)整不會影響最大反應發(fā)生的時間，因此可以使產(chǎn)生的加速度時程既滿足規(guī)范的目標反應譜，又保留了原地震動記錄的非平穩(wěn)特性和持續(xù)時間[22]。

如果設經(jīng)過k次調(diào)整后的加速度時程為akg（t），對于控制頻率ωk，若計算反應譜與目標反應譜之間的差值為δS，則定義疊加的加速度時程δag（t）為δag（t）=r·h（tm-t）B（t，ωk）， t≤tm（16）式中 tm為單自由度體系最大反應發(fā)生的時刻；B（t，ωk）為本文定義的時頻包線函數(shù)；r為振幅調(diào)整系數(shù)，可由計算反應譜Sa（ω）與目標反應譜STa（ω）的差值δS確定，即δS=Cr （17）式中C=∫tm0[h（tm-π）]2dτ（18）上式中，疊加的脈沖加速度函數(shù)表示為

h（t-tm）=eζωk（t-tm）cos（ωkt+k）， t≤tm （19）

式中 ζ為阻尼比；k為加速度脈沖函數(shù)的初始相位。

將C值代入式（17）確定振幅調(diào)整系數(shù)r，再將r代入式（16）就可以確定相應于頻率ωk的調(diào)整時程δag（t）。

經(jīng)過一次調(diào)整后的地震時程ak+1g（t）為ak+1g（t）=akg（t）+δag（t）（20） 將ak+1g（t）作為調(diào)整下一個控制點反應譜的初始時程，采用式（16）～（20）確定控制頻率的調(diào)整波。由于在初始地震動和調(diào)整時程中都計入了對頻率變化的控制，因此在完成對目標反應譜擬合的同時，可以近似模擬地震動頻率非平穩(wěn)特性。

在這個過程中，每一個頻率控制點的調(diào)整都會影響其他控制點，這些影響可以通過多次迭代的方法減輕，直至地震動時程的反應譜與目標反應譜的誤差滿足精度要求。

3 設計地震動擬合〖*8〗3.1 時程方案設計 本文以圖4（b）所示的β譜[23]作為目標反應譜進行地震動擬合，其中設計地震動峰值加速度Amax=0.268g，特征周期Tg=0.40 s，結構的阻尼比ζ=0.05，動力放大系數(shù)最大值βm=2.2，曲線下降段的衰減指數(shù)r=0.9。本文取80個控制點確定目標反應譜STa，允許誤差為5%。

圖4 原始地震動及其反應譜與目標譜的比較

Fig.4 Original ground motion and comparison between its response spectrum and the target response spectrum

選取1979年Imperial Valley-06水平地震記錄作為種子時程，如圖4（a）所示，其計算反應譜與選定的目標譜擬合情況如圖4（b）所示。為了研究地震動頻率非平穩(wěn)特性對結構非線性響應的影響，本文設計了4種不同的輸入方案：

方案1：Acc_wave1，以Imperial Valley地震動作為初始地震動，采用式（20）在時域內(nèi)進行調(diào)整，使之滿足目標反應譜；

方案2：Acc_wave2，僅考慮地震動強度非平穩(wěn)特性，采用三段式強度包絡函數(shù)在時域內(nèi)對初始地震動進行調(diào)整，包線參數(shù)提取Imperial Valley地震加速度記錄的5%和75%Arias強度對應的時刻，即t1=6.395 s，t2=16.07 s，c=0.1，為了考慮相位隨機性的影響，對于該時程方案，分別合成5個不同隨機相位的地震動時程，分別記為Acc_wave2（a），Acc_wave2（b），Acc_wave2（c），Acc_wave2（d），Acc_wave2（e）；

方案3：Acc_wave3，根據(jù)1.3節(jié)中給出的方法，提取Imperial Valley地震加速度記錄的時-頻包線函數(shù)B（t，ω），采用式（20）在時域內(nèi)進行調(diào)整，使其滿足目標反應譜；

方案4：Acc_wave4，根據(jù)1.2節(jié)中的方法，確定具有統(tǒng)計意義的時-頻包線函數(shù)B（t，ω），并采用式（20）在時域內(nèi)進行調(diào)整，使其滿足目標反應譜；根據(jù)Imperial Valley地震加速度記錄的實際條件選取主頻率參數(shù)，即基于二類場地、M[6.5，7.0）、R[40-60]水平向[15]確定的主頻參數(shù)模型，構造時-頻譜的強度包線參數(shù)采用方案2中的參數(shù)。

圖5 地震動加速度時程曲線

Fig.5 Acceleration time histories

圖6 地震動主頻率時變曲線

Fig.6 Time-varying curves of the predominant frequency

3.2 時程擬合結果分析

圖5，6分別給出了原始Imperial Valley時程、Acc_wave1到Acc_wave4擬合的加速度時程曲線圖及主頻率時變曲線圖，由于篇幅原因，這里只列出了方案2中5條不同隨機相位時程中的Acc_wave2（a）。與原始時程Imperial Valley相比，可以看出：（1）經(jīng)過時域調(diào)整得到的時程Acc_wave1很好地保留了原始時程的頻譜變化特性；（2）基于實際地震動提取的時-頻包線函數(shù)合成的地震動Acc_wave3，能夠較好地模擬地震動的頻率非平穩(wěn)特性；（3）基于統(tǒng)計參數(shù)的時-頻包線函數(shù)合成的地震動Acc_wave4能夠近似模擬地震動非平穩(wěn)特性，與實際地震記錄頻率隨時間的變化規(guī)律符合較好；（4）基于強度包線函數(shù)合成的時程Acc_wave2雖然在形狀上大致保留了原始記錄的強度變化情況，但頻率變化相對比較均勻，未能反映出頻率的時變特性。

圖7給出了4條地震時程計算反應譜與目標反應譜的擬合情況，可以看出，采用時域疊加脈沖響應函數(shù)的調(diào)整方法，每條地震動與目標譜的擬合效果都很好。圖8為4條時程功率譜的變化曲線，4條時程的功率譜變化趨勢也都比較接近。4種調(diào)整方法得到的主頻率比較接近，大約為2 Hz左右。

圖7 反應譜的擬合情況

Fig.7 Fitting of the response spectrum

圖8 功率譜變化曲線

Fig.8 Time-varying curves of the power spectrum4 結構的選型及非線性時程分析〖*2〗4.1 結構模型 本文僅討論比較規(guī)則的結構形式。選擇2個不同高度的鋼筋混凝土框架結構模型。模型1為3跨7層結構，模型2為5跨15層結構，立面圖如圖9所示。底層框架柱為600 mm×600 mm，中間層框架柱550 mm×550 mm，其余層框架柱500 mm×500 mm，所有框架梁為300 mm×500 mm，現(xiàn)澆板厚度為120 mm。混凝土強度等級柱子為C40、梁和板均為C30。樓面恒荷載為4 kN/m2，樓面屋面活荷載為2 kN/m2。模型的前3階振型周期及頻率如表1所示。

圖9 模型1，2的立面圖

Fig.9 Elevation drawing of model 1 and 2

表1 模型1，2前3階振型周期及頻率

Tab.1 The former 3 step vibration shape and frequency

模型振型/階周期/s頻率/Hz10.96991.0310120.91091.097830.77871.284212.44080.4097222.37450.421132.03090.49244.2 結構非線性時程反應分析

本文采用通用有限元軟件SAP2000建立三維框架模型，采用設計的4種時程輸入方案，分別對模型1，2進行結構非線性反應分析。

4.2.1 滯回曲線

圖10，11分別給出了2個結構底層剪力-位移變化曲線。可以看出，剪力-位移曲線呈現(xiàn)出明顯的非線性變化，結構進入非線性階段，并且滯回曲線面積較大，表明結構具有一定的耗能能力。

圖10 模型1底層剪力-位移曲線

Fig.10 Shear force-displacement for the bottom floor of model 1

圖11 模型2底層剪力-位移曲線

Fig.11 Shear force-displacement for the bottom floor of model 2

4.2.2 結果分析

下面將以時程方案1，即Acc_wave1作用下的計算結果為基準，分別對模型1，2的樓層位移響應和層間位移響應結果進行討論，其中方案2的結果是統(tǒng)計5條不同相位時程作用結果的平均值。模型1最大樓層位移曲線如圖12所示。可以看出：方案3和4作用下的結構樓層位移總體上偏大，而方案2計算的結果則偏小，且隨著樓層的增高，偏小程度越大。方案2，3，4下，結構頂點位移值與基準方案1結果的相對誤差如表2所示，相對誤差δ按下式計算δ=（D-D1）D1×100% （21）式中 D為方案2，3，4分別作用下的計算結果；D1為方案1頂點位移計算結果。若δ為正，則大于方案1的計算結果；若δ為負，則小于方案1的計算結果。對于模型1，D1=60.0 mm。從表中數(shù)據(jù)可以看出，只有方案2計算的結果偏小，且偏離程度較大。

圖12 模型1最大樓層位移

Fig.12 Maximum floor displacement of model 1

表2 模型1頂點位移及相對誤差

Tab.2 The top displacement and relative error of model 1

時程方案頂點位移/mmδ/%Acc_wave257.5-4.2Acc_wave361.62.7Acc_wave460.71.2

模型1層間位移曲線如圖13所示。可以看出，在較高的樓層處，結構的層間位移值比較小，且4種方案作用的結果幾乎接近；但在結構的薄弱層附近，方案3，4計算的位移響應結果偏大且比較接近方案1 的結果；方案2的結果明顯偏小，且偏離程度較大。表3給出了薄弱層附近的層間位移值及與基準

圖13 模型1層間位移

Fig.13 Maximum story displacement of model 1表3 模型1層間位移及相對誤差（單位：mm）

Tab.3 The story displacement and relative error of model 1 （Unit：mm）

樓層方案1方案2方案3方案4層間位移層間位移均值δ/%層間位移δ/%層間位移δ/%411.6811.31-3.1712.375.9112.426.34313.9812.95-7.3714.231.7914.382.86212.5711.71-6.8412.590.1612.47-0.8017.787.43-4.507.71-0.907.70-1.03

方案1結果的相對誤差。分析以上結果可以看出，只有方案2全部計算結果偏小，且偏離程度相對較大；方案3，4計算結果總體偏大，個別值偏小，但是偏離程度較小。

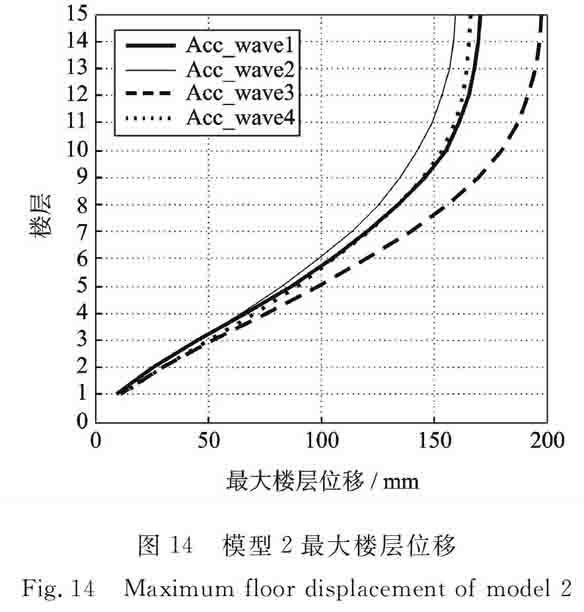
模型2最大樓層位移曲線、層間位移曲線分別如圖14，15所示。觀察可知：方案3的計算結果均偏大；方案2和4作用的結果總體上小于方案1的結果，且方案2作用下的樓層位移結果隨著樓層的增高偏離越來越大，薄弱層附近的層間位移結果相對偏小，且偏離程度較大。方案2，3，4下，結構頂點位移及層間位移與基準方案1結果的相對誤差如表4，5所示，對于模型2，D1=170.7 mm

圖14 模型2最大樓層位移

Fig.14 Maximum floor displacement of model 2

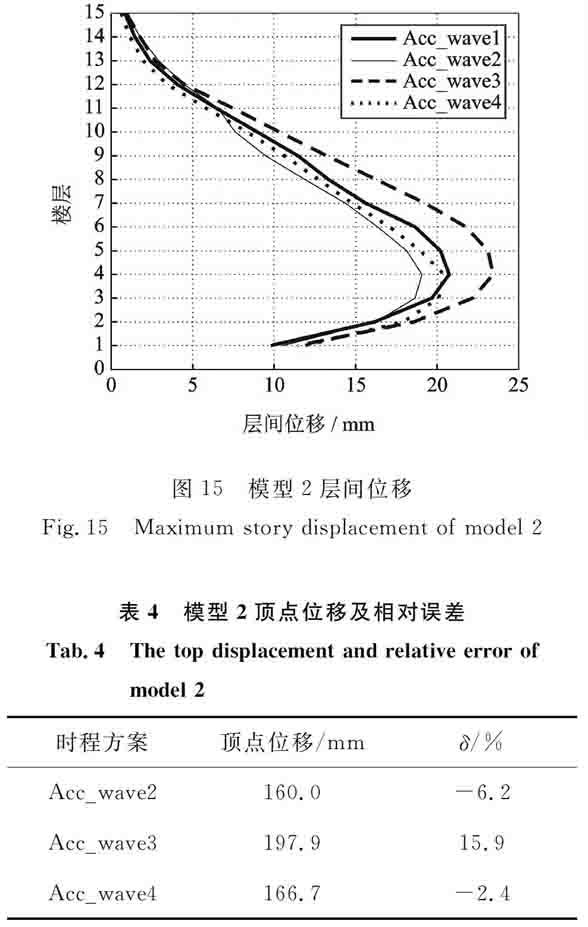
觀察可知：只有方案3的計算結果全部偏大；方案2和4作用的部分結果偏小，但方案4的結果更接近方案1的結果，尤其是薄弱層處。雖然模型1，2的自振周期不同，但是在方案2作用下，尤其是薄弱層附近的層間位移響應，相對其他時程方案偏小。圖15 模型2層間位移

Fig.15 Maximum story displacement of model 2

表4 模型2頂點位移及相對誤差

Tab.4 The top displacement and relative error of

model 2

時程方案頂點位移/mmδ/%Acc_wave2160.0-6.2Acc_wave3197.915.9Acc_wave4166.7-2.4

綜合以上分析：（1）基于原始時程提取的時頻包線函數(shù)合成的頻率非平穩(wěn)地震動基本上能夠安全地估計結構的響應；（2）僅考慮強度非平穩(wěn)特性合成的人工地震動，會低估結構的頂點位移響應和薄弱層的位移響應值；（3）本文提出的具有統(tǒng)計參數(shù)的時頻包線函數(shù)合成的頻率非平穩(wěn)地震動，相對于強度非平穩(wěn)地震動能夠較好地估計結構的地震響應，但是對于部分響應結果仍偏于保守，所以仍需進一步的研究改進。表5 模型2層間位移及相對誤差（單位：mm）

Tab.5 The story displacement and relative error of model 2 （Unit： mm）

樓層方案1方案2方案3方案4層間位移層間位移均值δ/%層間位移δ/%層間位移δ/%911.539.53-17.3513.3115.4410.65-7.63813.4211.93-11.1016.3521.8312.81-4.55715.6714.44-7.8519.2923.1014.86-5.17618.6616.39-12.1721.8617.1517.17-7.98520.3018.22-10.2523.1413.9919.06-6.11420.8119.13-8.0723.4712.7820.42-1.92319.7018.67-5.2322.2813.1020.142.23216.2216.300.4918.6214.8018.0010.9719.8210.537.2311.5317.4111.9621.795 結 論

本文通過引入具有統(tǒng)計意義的時-頻包線函數(shù)，建立了匹配多目標的頻率非平穩(wěn)地震動合成方法；并將不同方法擬合得到的4種地震加速度記錄作為輸入，對不同特性的規(guī)則鋼筋混凝土框架結構進行非線性時程分析，得出以下結論：

（1）在時域中通過疊加加速度脈沖響應函數(shù)，對初始地震動進行多目標的擬合方法能夠很好地保留原始地震動的非平穩(wěn)特性和持續(xù)時間，而且擬合精度較高；

（2）基于實際地震動提取的時-頻包線函數(shù)，能夠較好地模擬地震動的頻率非平穩(wěn)特性；

（3）基于統(tǒng)計參數(shù)構造的時-頻包線函數(shù)能夠近似模擬地震動非平穩(wěn)特性，符合實際地震加速度記錄頻率隨時間的變化規(guī)律；

（4）地震動的頻率非平穩(wěn)特性對結構的非線性響應有著不可忽視的影響，僅考慮強度非平穩(wěn)特性合成的人工地震動輸入存在低估結構的某些非線性響應的風險。

因此，在實際合成地震動過程中應該考慮頻率的非平穩(wěn)特性，合理估計結構的非線性響應，保證結構設計的安全性。

參考文獻：

[1] 胡聿賢，何 訓.考慮相位譜的人造地震動反應譜擬合[J]. 地震工程與工程振動，1986，6（2）：37—51.

HU Yu-xian， HE Xun. The response spectrum of the artificial ground motion based on phase spectrum[J]. Earthquake Engineering and Engineering Vibration，1986，6（2）：37—51.

[2] 董 娣，周錫元，徐國棟，等. 強震記錄頻率非平穩(wěn)特性的若干研究[J]. 地震工程與工程振動，2006，26（1）：22—29.

DONG Di， ZHOU Xi-yuan， XU Guo-dong， et al.Some studies on frequency non-stationarity of strong earthquake records[J]. Earthquake Engineering and Engineering Vibration，2006，26（1）：22—29.

[3] 楊 紅，曹 暉，白紹良. 地震波局部時頻特性對結構非線性響應的影響[J]. 土木工程學報， 2001，34（4）：78—82.

YANG Hong， CAO Hui， BAI Shao-liang. Effects of local time-frequency characteristics of earthquake waves on structural nonlinear responses[J]. China Civil Engineering Journal， 2001，34（4）：78—82.

[4] Hasgür Z. Nonstationary frequency effect of the ground motion upon the strength levels of the shear type RC structures[J]. Soil Dynamics and Earthquake Engineering， 1995，14（6）：453—461.

[5] Yong Li， Joel P Conte， Michele Barbato. Influence of time-varying frequency content in earthquake ground motions on seismic response of linear elastic systems[J]. Earthquake Engineering Structural Dynamics， 2016，45：1271—1291.

[6] 張翠然，陳厚群，涂 勁. 頻率非平穩(wěn)特性對大崗山拱壩非線性響應的影響[J]. 水力發(fā)電學報，2012，31（1）： 77—81.

ZHANG Cui-ran， CHEN Hou-qun， TU Jin.Influence of frequency non-stationary earthquakes accelerograms on the nonlinear responses of Dagangshan arch dam[J]. Journal of Hydroelectric Engineering， 2012，31（1）：77—81.

[7] 陳健云，李 靜，周 晶，等.地震動頻譜對小灣拱壩非線性響應的影響[J].振動工程學報，2003，16（2）：207—211.

CHEN Jian-Yun， LI Jing， ZHOU Jing， et al.The effects of ground motion on the nonlinear response spectrum of Xiaowan Arch Dam[J]. Journal of Vibration Engineering，2003，16（2）：207—211.

[8] 俞瑞芳，樊 珂，彭凌云，等.地震動非平穩(wěn)特性對結構反應影響的試驗研究[J]. 土木工程學報，2010，43（12）：13—20.

YU Rui-fang， FAN Ke， PENG Ling-yun， et al.Effect of non-stationary characteristics of ground motion on structural response[J]. China Civil Engineering Journal， 2010，43（12）：13—20.

[9] 曹 暉，林學鵬.地震動非平穩(wěn)特性對結構非線性響應影響的分析[J].工程力學，2006，23（12）：30—35.

CAO Hui， LIN Xue-peng. The effect of nonstationary characteristic of earthquake ground motion on the structural nonlinear responses[J]. Engineering Mechanics， 2006，23（12）：30—35.

[10]Nigam N C. Introduction to Random Vibrations[M]. MIT Press ： Cambridge，Mass，1983.

[11]胡聿賢，周錫元. 彈性體系在平穩(wěn)和非平穩(wěn)化地面運動下的反應，地震工程研究報告集第一集[M]. 北京：科學出版社，1962：33—50.

HU Yu-xian， ZHOU Xi-yuan.The First Report of the Study on the Seismic Response of Elastic Systems under Stationary and Non-stationary Ground Motions[M]. Beijing： Science Press， 1962：33—50.

[12]Amin M， Ang A H S. Nonstationary stochastic models of earthquake[J]. Journal of Engineering Mechanics. ASCE ，1968，94（2）：559—583.

[13]李英民，董銀峰，賴 明. 地震動瞬時譜估計的Unscented Kalman濾波方法[J]. 應用數(shù)學和力學， 2007，28（11）：1370—1378.

LI Ying-min， DONG Yin-feng， LAI Ming.Unscented Kalman filtering method for seismic instantaneous spectrum estimation[J]. Application Mathematics and Mechanics， 2007，28（11）：1370—1378.

[14]張郁山，趙鳳新.基于希爾伯特變換的非平穩(wěn)地震動模擬方法的驗證[J].地震學報，2014，36（4）： 686—697.

ZHANG Yu-shan， ZHAO Feng-xin.Validation of non-stationary ground motion simulation method based on Hilbert transform[J]. Acta Seismologica Sinica， 2014，36（4）：686—697.

[15]Yu Ruifang， Yuan Meiqiao， Yu Yanxiang. Developed empirical model for simulation of time-varying frequency in earthquake ground motion[J]. Earthquakes and Structures， 2015，8（6）：1463—1480.

[16]Grenier Y. Time-dependent ARMA modeling of nonstationary signals[J]. IEEE Trans， 1983，31（4）：899—911.

[17]Winger E. On the quantum correction for thermodynamic equilibrium[J]. Physical Review， 1932，40（1）：749—759.

[18]Morlet J， Arens G， Fourgeau E， et al. Wave propagation and sampling theory—Part II： Sampling theory and complex waves[J]. Geophysics， 1982，47（2）：222—236.

[19]Huang N E， Shen Z， Long S R， et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London A， 1998，454（1971）：903—995.

[20]葉 昆，李 黎. 基于設計加速度反應譜的地震動時程數(shù)值模擬[J].武漢理工大學學報，2009，31（8）：68—71.

YE Kun， LI Li. Numerical simulation of spectra-compatible seismic ground motion[J]. Journal of Wuhan University of Technology， 2009，31 （8）：68—71.

[21]袁美巧，俞瑞芳，俞言祥. 滿足時-頻統(tǒng)計特性的地震動時程調(diào)整[J]. 應用基礎與工程科學學報， 2010，18：162—172.

YUAN Mei-qiao， YU Rui-fang， YU Yan-xiang.Ground motion time history adjustment based on time frequency statistics[J]. Journal of Basic Science and Engineering， 2010，18：162—172.

[22]賀 瑞，秦 權.產(chǎn)生時程分析用得高質(zhì)量地面運動時程的新方法[J].工程力學，2006，23（8）：12—18.

HE Rui， QIN Quan. New methods for generating high quality acceleration time histories[J]. Engineering Mechanics， 2006，23（8）：12—18.

[23]中華人民共和國行業(yè)標準. 水工建筑物抗震設計規(guī)范（SL203-97） [S]. 北京：中國電力出版社， 2001.

Professionstandard of the people's republic of china. Specifications for seismic design of hydraulic structures（SL203-97） [S]. Beijing： China Power Press， 2001.

Simulation method of earthquake ground motion based on frequency-dependent

amplitude envelope function and its influence on the

structural nonlinear responses

QU Guo-yan， YU Rui-fang

（Institute of Geophysics， China Earthquake Administration， Beijing 100081， China）

Abstract： The non-stationarity of frequencies in the earthquake ground motion has an important effect on structural nonlinear responses. By introducing a frequency-dependent amplitude envelope function with statistical parameters to simulate the non-stationarity of frequencies in the earthquake ground motion， a method is developed for the non-stationary earthquake ground motion， which takes the response spectrum as the target. Taking the natural ground motion as the seed， four acceleration time histories for the same target spectrum are obtained by using four different methods. The results suggest that：（1） The fitting method developed could preserve the non-stationarity and duration of the original time history with higher fitting precision；（2） Based on the frequency-dependent amplitude envelope function of the natural ground motion， the earthquake ground motion can be used to simulate the non-stationarity of frequency better；（3） The one based on the frequency-dependent amplitude envelope function with statistical significance is able to simulate the non-stationarity of frequencies approximately， which agrees with the frequency time-variation of the natural ground motion. Taking the four time histories as input， the nonlinear time-history analysis of the reinforced concrete frame structure with 7 and 15 layers are presented. The results show that there exists the risk of underestimating the reinforced concrete structural nonlinear response under the earthquake ground motion only considering the non-stationarity of the intensity. Therefore， the non-stationarity of frequencies in the earthquake ground motion should be considered in the simulation of the artificial ground motion. In this way， the structural nonlinear responses could be estimated reasonably and the safety of the structure design can be guaranteed.

Key words： random vibration； earthquake ground motion； structural nonlinear responses； non-stationarity of frequency； simulation of earthquake ground motion