變頂高尾水洞水輪機調節系統哈密頓模型

張浩 許貝貝 陳帝伊

摘要： 為了研究變頂高尾水洞水輪機調節系統瞬態能量變化特征、揭示變頂高尾水洞水輪機調節系統穩定機理，對引水系統動力學方程進行改進，使其更準確描述變頂高尾水洞明滿流運動特性。利用廣義哈密頓系統在描述能量流變化的優勢，構造了變頂高尾水洞水輪機調節系統哈密頓函數，將傳統水輪機調節系統仿射非線性方程轉化為哈密頓系統形式。首先，從理論上驗證了在廣義哈密頓理論框架下，變頂高尾水洞水輪機調節系統能量流的變化與實際物理系統的一致性；其次，通過數值模擬表明，所選擇的哈密頓函數可以有效地描述變頂高尾水洞水輪機調節系統在瞬態過程中能量變化特征；最后，探究了在無負荷擾動、階躍負荷擾動和隨機負荷擾動情況下，變頂高水輪機調節系統的能量變化規律。

關鍵詞： 水動力學； 水輪機調節系統； 變頂高尾水洞； 哈密頓模型； 負荷擾動

中圖分類號： TV136+.1； TK730.1； TV737文獻標志碼： A文章編號： 1004-4523（2018）02-0323-06

DOI：10.16385/j.cnki.issn.1004-4523.2018.02.016

引言

尾水系統是水電站系統的重要組成部分，主要有三種形式，分別是無壓隧洞、有壓隧洞和變頂高尾水洞[1-3]。變頂高尾水洞是水電站尾水系統的一種新形式，在一定條件下可以替代尾水調壓室[4-6]。變頂高尾水隧洞的特點是下游水位與洞頂的某一處相銜接，將尾水洞分為有壓滿流段和無壓明流段。當下游處于低水位時，下游水位與洞頂較低處相銜接，此時有壓滿流段短，而無壓明流段長，可以控制尾水管進口的真空度不超過規范的要求。變頂高尾水洞的工作原理是利用下游水位的變化，確定尾水洞有壓滿流段的長度不超過極限長度，使整個尾水系統始終滿足對尾水管進口處真空度的要求。但變頂高尾水洞中存在明滿混合流現象，嚴重影響水電站系統安全穩定運行[7-9]，因此需要深入地探究變頂高尾水洞水輪機調節系統的能量流變化規律。

與傳統拉格朗日體系下的仿射微分方程組不同，廣義哈密頓系統善于描述系統內部能量供給、耗散及與外部能量交換[10-11]。隨著廣義哈密頓系統理論的發展，其結構矩陣和阻尼矩陣能夠提供更多系統參數信息[12]。

目前對變頂高尾水洞水輪機調節系統和水輪機調節系統哈密頓模型的研究已取得一定進展，如：文獻[13]運用Hopf分岔理論研究了變頂高尾水洞水電站水輪機調節系統的穩定性，給出了Hopf分岔的代數判據，繪制了系統穩定域；文獻[14]通過將水輪機及其水力系統納入廣義哈密頓框架分析了其控制的動力學機制并對非線性水輪機的哈密頓建模問題進行了研究；文獻[15]通過正交分解實現方法將非線性水輪機系統轉化為哈密頓系統并進行能量流分析，仿真表明哈密頓函數可以較好地反映系統的內部關聯和外部聯系；文獻[16]從非恒定漸變流動的Bernoulli方程出發，研究了甩負荷工況下變頂高尾水管進口真空度近似計算公式，通過物理實驗證明該近似公式可應用于工程初步設計；文獻[17]通過引入變頂高尾水洞明滿分界面處水體交替運動的連續性方程，分析了變頂高尾水洞機組運行的穩定性；文獻[18]針對一管多機水輪機調節系統建立了哈密頓模型并分析了該模型在隨機負荷下的動力學特性。然而，系統研究變頂高尾水洞水輪機調節系統哈密頓模型的成果相對較少，本文利用廣義哈密頓理論將變頂高尾水洞水輪機調節系統轉化為其對應的哈密頓系統形式。分別在無負荷擾動、階躍負荷擾動和隨機負荷擾動情況下，研究變頂高尾水洞水輪機調節系統瞬態能量變化規律。

第2期張浩，等：變頂高尾水洞水輪機調節系統哈密頓模型振 動 工 程 學 報第31卷1變頂高尾水洞水輪機調節系統模型

變頂高尾水洞水電站引水發電系統如圖1所示。

圖1變頂高尾水洞水電站示意圖

Fig.1Sketch of a hydropower station tailrace tunnel with

inclined ceiling

在負荷波動過程中，尾水洞中明滿流的交替運動會引起尾水洞中水流慣性變化；另一方面明流段水位波動也會影響機組工作水頭。文中，h=（H-H0）/H0，q=（Q-Q0）/Q0，x=（n-n0）/n0，y=（Y-Y0）/Y0，mt=（Mt-Mt0）/Mt0，mg=（Mg-Mg0）/Mg0為各變量的相對偏差值，下標“0”表示初始時刻值。B為變頂高尾水洞寬度，n為機組轉速，Y為導葉開度，α為變頂高尾水洞頂坡角，Hx為明滿流分界面處水深，c為明流段明渠波速，Mt為水輪機動力矩，Mg為水輪機阻力矩，Ta為機組慣性時間常數，λ為尾水洞斷面系數，Kp為比例增益，Ki為積分增益，mg為負荷擾動。

由文獻[13]可知，變頂高尾水洞水電站的壓力管道動力方程為h=-Tws+Twxdqdt-2hfH0q-zy （1）其中，Tws=LVgH0，Twx=LxVxgH0且zy=ZyH0。L為壓力管道長度，f為壓力管道斷面面積，Q為機組流量，V為管道水流流速，hf為壓力管道水頭損失，Lx為明滿流分界面任意瞬態時刻相對初始位置的運動距離，Vx為明滿流分界面處水流流速，Tws為穩態水流慣性時間常數，Twx為暫態水流慣性時間常數，H為機組工作水頭，Zy為任意瞬態時刻相對初始水位的明流段水位變化值。

依據文獻[17]假定，對于一般的變頂高尾水洞（洞頂坡度不超過5%），明滿流分界面處水流連續性方程可以表示為Q-Q0Δt=LxZyB/λ （2）進而可知，Lx=λQ0cBtanαq，故Twx=λQ0gH0cBtanαq。由Zy=Lxtanα得zy=λQ0H0cBq。采用Twx和zy的表達式可將式（1）轉化為h=-λQ0VxgH0cBtanαqdqdt-Twsdqdt-2hfH0+λQ0H0cBq （3）水輪機動態特性表達式為mt=ehh+exx+eyy，q=eqhh+eqxx+eqyy （4）式中eh，ex，ey為水輪機力矩傳遞系數；eqh，eqx，eqy為水輪機流量傳遞系數。

發電機和負載動態特性為Tadxdt=mt-mg+egx （5）液壓隨動系統動態特性為dydt=-Kpdxdt-Kix （6）綜合式（3）～（6），獲得變頂高尾水洞水輪機調節系統非線性模型為=-2hfH0+λQ0H0cB+1eqhq+eqxeqhx+eqyeqhyλQ0VxgH0cBtanαq+Tws

=1Taeheqhq+ex-eheqheqx-egx+

ey-eheqheqyy-mg

=-KpTaeheqhq-KpTaex-eheqheqx-eg+Kix-

KpTaey-eheqheqyy+KpTamg （7）2系統哈密頓模型

由式（7）可得，變頂高尾水洞水輪機調節系統的仿射非線性方程為=f（x）+g（x）u （8）式中=[，，]T，g（x）=[0，0，1Ty]T，f（x）=[X1，X2，X3]T，X1=-2hfH0+λQ0H0cB+1eqhq+eqxeqhx+eqyeqhyλQ0VxgH0cBtanαq+Tws，X2=1Ta·eheqhq+ex-eheqheqx-egx+ey-eheqheqyy-mg，X3=-KpTaeheqhq-KpTaex-eheqheqx-eg+Kix+KpTamgKpTaey-eheqheqy，Ty為接力器時間常數，u為輸入控制信號。

依據文獻[14-15]，哈密頓系統的自然輸出為yH=g（x）THX=-Pm （9）式中Pm為水輪機出力相對偏差值。

由水輪機動態特性和Pm=mtw可知，水輪機出力相對偏差值為Pm=π30xeheqhq-eqxx-eqyy+exx+eyy （10）進一步地，由式（9）和（10）可得哈密頓函數為H=πTyy（2eheqxx+eheqyy-2ehq-

2eqhexx-eqheyy）/（60eqh） （11）采用正交分解實現方法，將仿射非線性方程（8）轉化為哈密頓模型=[J（x）+P（x）]Hx+g（x）u （12）式中Jx為反對稱矩陣，Px為對稱矩陣，且有ftdx=fx-〈fx，Hx〉Hx2Hxx （13）

Px=〈fx，Hx〉Hx2I3=N00

0N0

00N （14）式中N=〈fx，Hx〉Hx2。Jx=1Hx2[ftdxHTx-

HxfTtdx]=1Hx2·

0J12J13

J120J23

J13J230 （15）式中J12=Hx2f1-Hx1f2，J13=Hx3f1-Hx1f2，J23=Hx3f2-Hx2f3。

3能量流分析

系統矩陣Px可進一步分解為Px=1Hx2〈fx，H〉=

Sx-Rx （16）其中，Sx=sx00

0sx0

00sx，N=1Hx2〈fx，H〉=1Hx2·f1Hx1+f2Hx2+f3Hx3=1Hx2·

Mdqdt+KpDTaeqhxey-CTaeqhmt-KpDTaeqhpm-DeqhKix2，Rx=rx00

0rx0

00rx，M=-2πTyehxyeqh，C=πTyy4eqhexx-4eheqhx+2ehq-eheqyy+eqheyy，D=πTy（eheqxy-eqhexy-2ehq+2eheqxx+eheqyy-2eqhexx-eqheyy）。當取理想水輪機傳遞系數時，M>0，C>0，D>0。故rx=1Hx2·CTaeqhmt+KpDTaeqhpm+DeqhKix2，sx=1Hx2·Mdqdt+KpDTaeqhxey。

據文獻[12]，系統能量流定義如下。系統能量耗散為HxTRxHx=CTaeqhmt+KpDTaeqhpm+DeqhKix2 （17）式（17）說明系統能量耗散包括機組克服阻力所需的空載功耗和水輪機輸出功率以及由于轉速變化產生的阻尼功率。

系統內部能量供給為HxTSxH〖〗x=Mdqdt+KpDeyTaeqhx （18）式（18）第一項表示流量變化產生的慣性能量，第二項反映在水輪機調節系統中，能量的產生與機組轉速直接相關。

式（17），（18）中各項能量均為廣義能量，在廣義能量描述下，能量流的變化和實際系統一致且物理意義清晰。

不同哈密頓函數反映的系統內部關聯機制不同，將變頂高尾水洞水輪機調節系統納入廣義哈密頓理論框架下的核心問題是恰當哈密頓函數的確定[15]。為驗證本文所選擇哈密頓函數的有效性，分別在無負荷擾動、階躍負荷擾動和隨機負荷擾動情況下，利用數值模擬對比分析瞬態過程中水輪機出力和水輪機能量的變化規律。

4變頂高尾水洞水電站系統哈密頓仿真分析變頂高尾水洞水電站系統基本資料如下：額定水頭H0=70.7 m，額定流量Q0=466.7 m3/s，Ta=6 s，B=10.0 m，Tws=3.20 s，hf=0.1 m，Hx=23 m，tanα=0.03，λ=3。水輪機傳遞系數為：eh=1.9，ex=-0.8，ey=1，eqh=0.5，eqx=0.5，eqy=0.6，eg=0。仿真初值條件為（q，x，y）=（0，0，0），mg表示負荷擾動。

分析圖2可知，在無負荷擾動情況下（mg=0），水輪機出力無變化，且哈密頓函數在該過程也無變動，說明本文所選擇的哈密頓函數在無負荷擾動情況下的變化與變頂高尾水洞水輪機調節系統穩態過程中的能量變化較為一致。

圖2無負荷擾動下水輪機出力和哈密頓函數的變化

Fig.2Changes of the turbine output and Hamiltonian

function without load disturbance

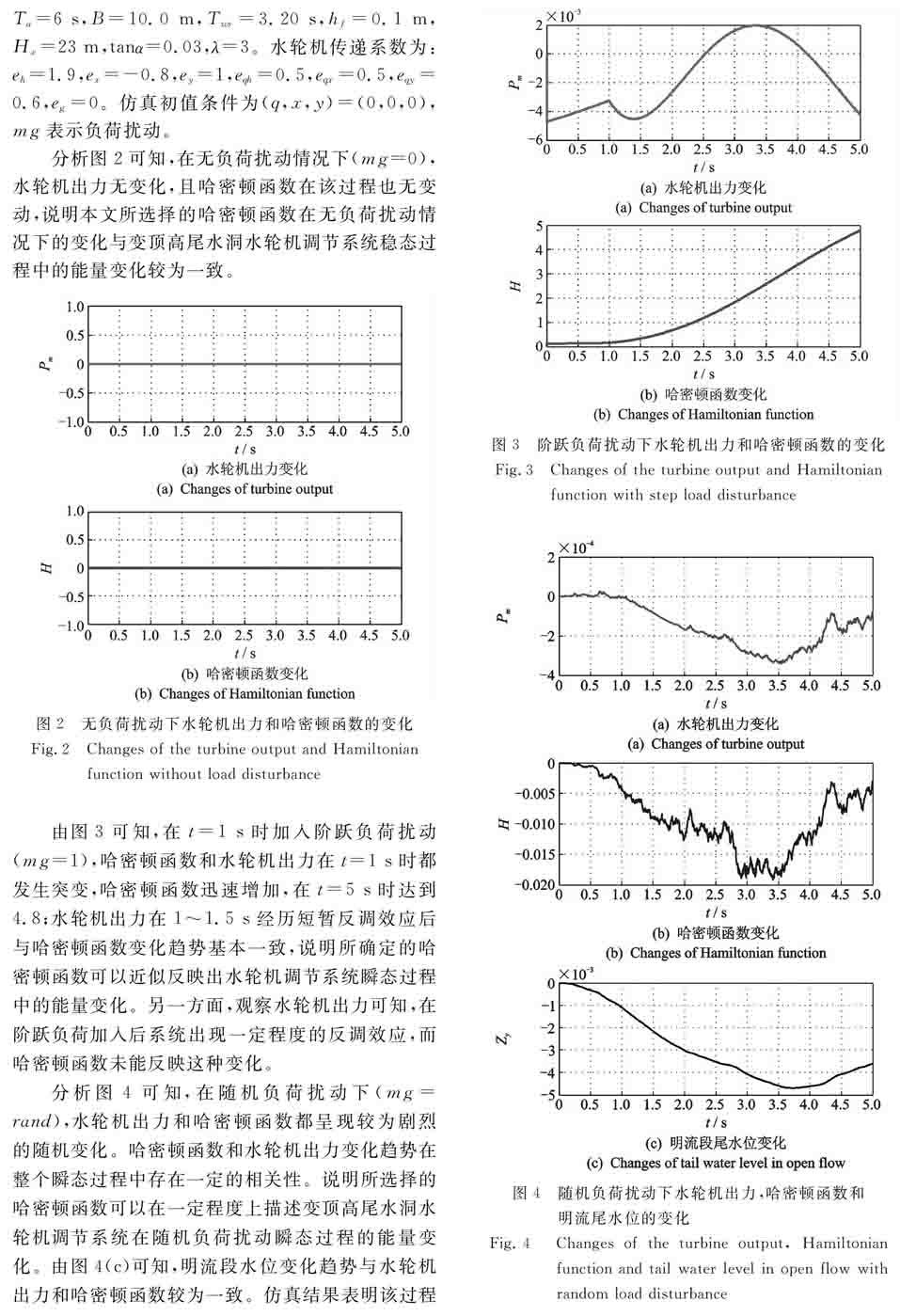
由圖3可知，在t=1 s時加入階躍負荷擾動（mg=1），哈密頓函數和水輪機出力在t=1 s時都發生突變，哈密頓函數迅速增加，在t=5 s時達到4.8；水輪機出力在1～1.5 s經歷短暫反調效應后與哈密頓函數變化趨勢基本一致，說明所確定的哈密頓函數可以近似反映出水輪機調節系統瞬態過程中的能量變化。另一方面，觀察水輪機出力可知，在階躍負荷加入后系統出現一定程度的反調效應，而哈密頓函數未能反映這種變化。

分析圖4可知，在隨機負荷擾動下（mg=rand），水輪機出力和哈密頓函數都呈現較為劇烈的隨機變化。哈密頓函數和水輪機出力變化趨勢在整個瞬態過程中存在一定的相關性。說明所選擇的哈密頓函數可以在一定程度上描述變頂高尾水洞水輪機調節系統在隨機負荷擾動瞬態過程的能量變化。由圖4（c）可知，明流段水位變化趨勢與水輪機出力和哈密頓函數較為一致。仿真結果表明該過程圖3階躍負荷擾動下水輪機出力和哈密頓函數的變化

Fig.3Changes of the turbine output and Hamiltonian

function with step load disturbance圖4隨機負荷擾動下水輪機出力，哈密頓函數和

明流尾水位的變化

Fig.4Changes of the turbine output， Hamiltonian function and tail water level in open flow with random load disturbance中，由于負荷減小，水輪機出力隨之減小，則進入系統水流流量減少導致明流段水位降低。此外，對比水輪機出力變化和哈密頓函數變化可知，在存在一定相關性的基礎上，哈密頓函數變化幅度大于水輪機出力變化幅度，說明在該隨機負荷擾動瞬態過程中，該哈密頓函數具有較好的靈敏性。

5結論

在變頂高尾水洞水輪機調節系統仿射非線性模型基礎上，通過哈密頓正交分解獲得變頂高尾水洞水輪機調節系統哈密頓函數。理論分析表明，在廣義能量描述下，系統能量流的變化較為合理。利用數值模擬驗證了所選擇的哈密頓函數能在一定程度上反映水輪機調節系統在穩態和瞬態過程中能量的變化信息。深入分析了變頂高尾水洞水輪機調節系統在無負荷擾動、階躍負荷擾動和隨機負荷擾動下，系統能量變化規律。

將變頂高尾水洞水輪機調節系統納入廣義哈密頓理論框架下，分析廣義哈密頓系統結構矩陣獲得系統內部的關聯信息，本文的建模方法和仿真研究為分析水輪發電機組瞬態能量流特性提供了一種新視角。

參考文獻：

[1]賈偉， 劉晶石， 龐立軍， 等. 抽水蓄能電站水泵水輪機的動靜干涉與振動分析[J]. 振動工程學報， 2014， 27（4）：565—571.

Jia Wei， Liu Jingshi， Pang Lijun， et al. Analysis on rotor-stator interaction and vibration of pump turbine in pumped storage power station[J]. Journal of Vibration Engineering， 2014， 27（4）：565—571.

[2]凌代儉， 陶陽， 沈祖詒. 考慮彈性水擊效應時水輪機調節系統的Hopf分岔分析[J]. 振動工程學報， 2007， 20（4）：374—380.

Ling Daijian， Tao Yang， Shen Zuyi. Hopf bifurcation analysis of hydraulic turbine governing systems with elastic water hammer effect[J]. Journal of Vibration Engineering， 2007， 20（4）：374—380.

[3]張輝， 胡釙. 多機共尾水調壓室流道結構水輪機調節振蕩研究[J]. 水利學報，2015，46（2）：229—238.

Zhang Hui， Hu Po. Study on regulating oscillation in multi hydro turbine generators sharing flow channel structure of tailrace surge tank[J]. Journal of Hydraulic Engineering， 2015，46（2）：229—238.

[4]郭文成， 楊建東， 王明疆. 基于Hopf分岔的變頂高尾水洞水電站水輪機調節系統穩定性研究[J]. 水利學報， 2016， 47（2）：189—199.

Guo Wencheng， Yang Jiandong， Wang Mingjiang. Stability analysis of hydro-turbine governing system of hydropower station with inclined ceiling tailrace based on Hopf bifurcation[J]. Journal of Hydraulic Engineering， 2016， 47（2）：189—199.

[5]周昆雄， 張立翔， 曾云. 機-電偶聯條件下水力發電系統暫態分析[J]. 水利學報， 2015， 46（9）：1118—1127.

Zhou Kunxiong， Zhang Lixiang， Zeng Yun. Transient modeling of hydraulic electricity-generating system in water-machine-electricity coupling conditions[J]. Journal of Hydraulic Engineering， 2015， 46（9）：1118—1127.

[6]馮建軍， 武樺， 吳廣寬， 等. 偏工況下混流式水輪機壓力脈動數值仿真及其改善措施研究[J]. 水利學報， 2014， 45（9）：1099—1105.

Feng Jianjun， Wu Hua， Wu Guangkuan， et al. Evaluation of soil salts leaching in cotton field after mulched drip irrigation with brackish water by freshwater flooding[J]. Journal of Hydraulic Engineering， 2014， 45（9）：1099—1105.

[7]周建旭， 張健， 劉德有. 雙機共變頂高尾水洞系統小波動穩定性研究[J]. 水利水電技術， 2004， 35（12）：64—67.

Zhou Jianxu， Zhang Jian， Liu Deyou. Study on small fluctuation in system of two units and common tail-tunnel with sloping ceiling[J]. Water Resources and Hydropower Engineering， 2004， 35（12）： 64—67.

[8]朱文龍， 周建中， 夏鑫， 等. 基于水電機組運行工況的水輪機壓力脈動診斷策略[J]. 振動與沖擊， 2015， 34（8）：26—30，40.

Zhu Wenlong， Zhou Jianzhong， Xia Xin， et al. A novel diagnosis strategy for hydraulic turbine pressure pulsation based on operating state of a hydroelectric generating unit[J]. Journal of Vibration and Shock， 2015， 34（8）：26—30，40.

[9]安華， 楊建東. 基于1D-3D耦合方法的變頂高尾水洞明滿混合流的研究[J]. 水力發電學報， 2015， 34（5）：108—113.

An Hua， Yang Jiandong. Study on free surface-pressurized flows in tailrace tunnel with sloping ceiling by 1D-3D coupling approach[J]. Journal of Hydroelectric Engineering， 2015， 34（5）： 108—113.

[10]徐新生， 郭杏林， 馬國軍， 等. 旋轉系統中彈性結構振動問題的哈密頓體系方法[J]. 振動工程學報， 2003， 16（1）：36—40.

Xu Xinsheng， Guo Xinglin， Ma Guojun， et al. A method of hamiltonian formulation for elastic structural vibration in rotating system[J]. Journal of Vibration Engineering， 2003， 16（1）：36—40.

[11]滕俊超， 朱位秋. 諧和與寬帶隨機激勵下擬可積哈密頓系統的最優時滯控制[J]. 振動工程學報， 2016， 29（2）：207—213.

Teng Junchao， Zhu Weiqiu. Optimal time-delay control of quasi integrable Hamiltonian systems under combined harmonic and wide-band random excitations[J]. Journal of Vibration Engineering， 2016， 29 （2）：207—213.

[12]朱位秋， 黃志龍， 應祖光. 非線性隨機動力學與控制的哈密頓理論框架[J]. 力學與實踐， 2002， 24（3）：1—9.

Zhu Weiqiu， Huang Zhilong， Ying Zuguang. Hamiltonian framework of nonlinear stochastic dynamics and control[J]. Mechanics and Engineering， 2002， 24（3）：1—9.

[13]郭文成， 楊建東， 王明疆. 基于Hopf分岔的變頂高尾水洞水電站水輪機調節系統穩定性研究[J]. 水利學報， 2016， 47（2）：189—199.

Guo Wencheng， Yang Jiandong， Wang Mingjiang. Stability analysis of hydro-turbine governing system of hydropower station with inclined ceiling tailrace based on Hopf bifurcation[J]. Journal of Hydraluic Engineering， 2016， 47（2）：189—199.

[14]曾云， 張立翔， 徐天茂， 等. 彈性水擊下非線性水輪機的哈密頓模型[J]. 排灌機械工程學報， 2010， 28（6）：515—520.

Zeng Yun， Zhang Lixiang， Xu Tianmao， et al. Hamiltonian model of nonlinear hydraulic turbine with elastic water column[J]. Journal of Drainage and Irrigation Machinery Engineering， 2010， 28（6）：515—520.

[15]曾云， 王煜， 張成立. 非線性水輪發電機組哈密頓系統研究[J]. 中國電機工程學報， 2008， 28（29）：88—92.

Zeng Yun， Wang Yu， Zhang Chengli. Study for Hamiltonian System of Nonlinear Hydraulic Turbine Generating Unit[J]. Proceeding of the CSEE， 2008， 28（29）：88—92.

[16]繆明非， 張永良. 變頂高尾水系統尾水管進口真空度的近似公式[J]. 水力發電學報， 2011， 30（2）：49—53.

Miu Mingfei， Zhang Yongliang. Approximate formula for vacuum degree at the inlet of a draft tube in a tailrace with inclined ceiling[J]. Journal of Hydroelectric Engineering， 2011， 30（2）：49—53.

[17]賴旭， 陳鑒治， 楊建東. 變頂高尾水洞水電站機組運行穩定性研究[J]. 水力發電學報， 2001， （4）：102—107.

Lai Xu， Chen Jianzhi， Yang Jiandong. Stability Analysis of Hydropower Station With Inclined Ceiling Tailrace[J]. Journal of Hydroelectric Engineering， 2001， （4）：102—107.

[18]Xu B B， Wang F F， Chen D Y， et al. Hamiltonian modeling of multi-hydro-turbine governing systems with sharing common penstock and dynamic analyses under shock load[J]. Energy Conversion and Management， 2016， 108：478—487.

Hamiltonian model of a hydro-turbine governing system

with inclined ceiling tailrace

ZHANG Hao， XU Bei-bei， CHEN Di-yi

（College of Water Resources and Architectural Engineering （Institute of Water Resources and Hydropower Research），

Northwest A & F University， Yangling 712100， China）

Abstract： To better study the transient energy change and stabilization mechanism of the hydro-turbine governing system with inclined ceiling tailrace， considering the nonlinear model of the hydro-turbine governing system with inclined ceiling tailrace， the momentum equation of pipeline system is developed in order to accurately describe the dynamic characteristic of the interface of free surface pressurized flow in tailrace. To make full use of strengths of generalized Hamiltonian system in describing energy flow， the Hamilton function of the hydro-turbine with inclined ceiling tailrace is constructed and the traditional affine nonlinear equations for the hydro-turbine governing system with inclined ceiling tailrace are converted into Hamiltonian system. Firstly， the energy flow of the hydro-turbine governing system with inclined ceiling tailrace in the framework of generalized Hamiltonian theory is proved theoretically to be consistent with the real system. Moreover， the simulation results indicate that the constructed Hamiltonian function can effectively describe the energy change of the hydro-turbine governing system with inclined ceiling tailrace in transient process. The regularity of the energy change for the hydro-turbine governing system with inclined ceiling tailrace is deeply studied under no-load， step load and random load， respectively.

Key words： hydrodynamics； hydro-turbine governing system； inclined ceiling tailrace； Hamiltonian model； load disturbance