基于VAR-VEC組合模型的CCI與PPI關系研究

羅耀寧，唐國強，繆巧芬

（桂林理工大學 理學院，廣西 桂林 541004）

0 引言

消費者信心指數（CCI）和生產價格指數（PPI）都是衡量我國經濟發展趨勢的重要宏觀經濟指標。消費者信心指數（CCI）是反映消費者信心強弱的指標，是綜合反映并量化消費者對當前經濟發展形勢評價和對經濟前景、收入水平、收入預期以及消費心理狀況的主觀性感受，是預測經濟未來走勢和消費未來趨向的一個先行指標，是監測經濟周期是否發生變化的重要依據。生產價格指數（PPI）是衡量工業企業產品出廠價格變動趨勢和變動情況的指標，是反映某一時期生產領域價格變動狀況的重要經濟指數，也是制定有關經濟政策和國民經濟核算必不可缺的依據。與居民消費價格指數（CPI）不同，生產價格指數（PPI）主要的目的是衡量企業購買的一籃子物品和勞務的總費用。因為企業最終會把總費用以更高的消費價格轉移給消費者，所以，通常認為生產價格指數的變動來預測消費物價指數的變動是有意義的。

不少學者對CCI和PPI的模型和預測進行研究，張曉帥等（2012）[1]運用改進灰色模型對我國CCI進行預測；徐婷（2013）[2]利用時間序列模型方法對我國CCI建立了組合預測模型；董大勇等（2016）[3]應用ARIMA模型對PPI進行建模，并做出了短期的預測；趙永興等（2013）[4]用PPI月度數據來構建EGARCH（1，1）模型，說明了PPI存在ARCH效應。還有很多文獻分別研究CCI、PPI與其他經濟指標之間的關系。何毅等（2012）[5]探討了CCI對CPI的影響效應；李躍輝等（2012）[6]指出CPI、CCI和PMI（采購經理人指數）之間存在長期穩定的協整關系；何躍等（2016）[7]探討PPI對GDP的預警作用，從而為宏觀經濟政策提供依據。以上文獻研究表明了CCI和PPI分別與CPI存在一定關系，并且兩者都是反映經濟發展趨勢的重要指數。本文通過擬合VAR-VEC組合模型探討CCI與PPI之間是否存在關系。

1 理論與建模步驟

1.1 VAR模型

向量自回歸模型（VAR模型）在1980年由西姆斯（Sims C A）提出，主要應用于分析和預測隨機擾動對系統的動態沖擊，沖擊的大小、正負及持續的時間[8]。VAR模型是在數據的統計性質基礎上建立模型，它把系統中每一個內生變量作為系統中所有內生變量的滯后階數來構建模型，從而將單變量自回歸模型推廣到多元時間序列變量組成的向量自回歸模型中去。

設 Yt=(y1t，y2t，…，ynt)′是 n×1階的時間序列向量，p階VAR模型（記為VAR（p））的表達式為：

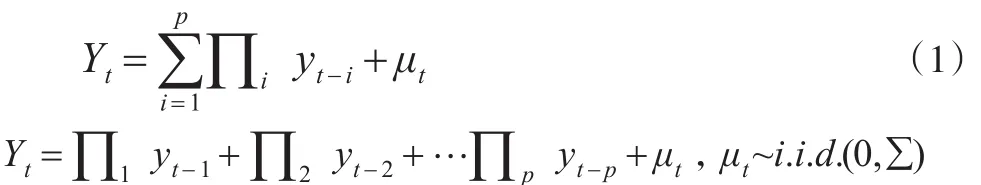
其中，p是最大滯后階數，∏i(是第i個待估參數n×n階矩陣，μt是n×1階隨機誤差列向量，∑是n×n階協方差矩陣。

VAR(p)模型的穩定條件是要求特征方程的根都落在單位圓以內。

1.2 Johansen協整檢驗[9]

1990年Johansen與Juselius一起提出了Johansen協整檢驗，它是基于VAR模型檢驗回歸系數的一種檢驗方法，也可以用于多變量之間的協整檢驗。

對于n個時間序列Yt=(y1t，y2t，…，ynt)T，可以利用協整定義討論這n個變量之間是否存在協整關系。協整的定義如下：

n維向量時間序列Yt的分量間d'b階協整，記為Yt～CI(d'b)，如果滿足：

（1）Yt～I(d)，要求Yt的每一個分量都是d階單整的；（2）存在非零向量 β ，使得 β′Yt～Ι(d-b)，0＜b≤d 。簡稱yt是存在協整關系的，向量β為協整向量。對于n維向量時間序列Yt至多存在n-1個線性無關的協整向量。

1.3 脈沖響應函數的基本思想[10]

本文以含有兩個變量的VAR（2）模型為例，介紹脈沖響應函數分析方法的基本思想。

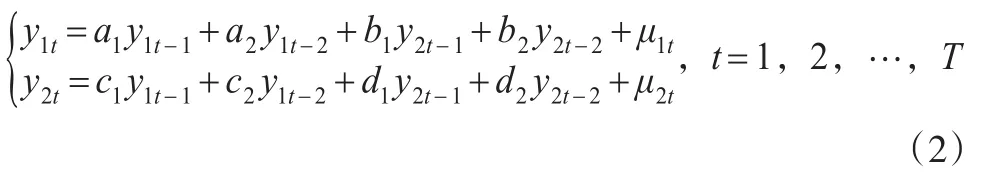
式（2）中是待估參數，隨機擾動項μt=(μ1t'μ2t)′，假設是具有以下性質的白噪聲向量：

Ε(μit)=0，對于?t，i=1'2

var(μt)=Ε(μtμt′)=∑，對于?t

Ε(μitμis)=0，對于?t≠s，i=1'2

假設是從第0期開始活動，且設 y1t-1=y1t-2=y2t-1=y2t-2=0，又設在第0期給定了擾動項 μ10=1，μ20=0，且其他擾動項均為0，即 μ1t=μ2t=0(t = 1，2，…) ，稱此為第0期對 y1t的脈沖響應。同樣地，當擾動項μ10=0，μ20=1，且其他擾動項均為0，即 μ1t=μ20=0(t = 1，2，…) ，稱此為第0期對y2t的脈沖響應。

1.4 VEC模型[10]

Engle和Granger將協整理論與誤差修正模型結合起來，建立了向量誤差修正模型，即VEC模型。只要變量之間存在著協整關系，就可以由自回歸分布滯后模型導出誤差修正模型（ECM）。而在VAR模型中每一個方程都是一個自回歸分布滯后模型，因此，可以認為VEC模型是含有協整約束的VAR模型。

根據協整方程可得到VEC模型的表達式：

其中是 yt經過差分變換的平穩值，α為系數向量，β為協整向量，μt為隨機擾動向量。

式（3）也可以表示為：

式（4）中的每一個方程都是一個誤差修正模型。其中ecmt-1=β′yt-1是誤差修正項向量，反映變量之間的長期均衡關系。系數向量α反映了變量之間偏離長期均衡狀態時，將其調整到均衡狀態的調整速度。所有作為解釋變量的差分項的系數反映各變量的短期波動對作為被解釋變量的短期變化的影響。

1.5 基于VAR-VEC組合模型的建模步驟

本文通過建立一個VAR-VEC組合模型，運用協整檢驗、脈沖響應函數等分析方法探究CCI與PPI的關系。建模步驟如下：

（1）為消除季節趨勢和異方差性、減少波動，分別對CCI序列、PPI序列取對數，記為LNCCI序列和LNPPI序列；

（2）對CCI、PPI、LNCCI、LNPPI序列進行平穩性檢驗，并對非平穩序列做平穩處理；

（3）根據AIC準則和SC準則確定VAR模型的最大滯后階數p；

（4）以最大滯后階數p構建VAR（p）模型，并利用AR根的圖表驗證VAR（p）模型的穩定性；

（5）對一階單整序列LNCCI和LNPPI做Johansen協整檢驗，檢驗兩者之間是否存在長期協整關系；

（6）在協整檢驗的基礎上，做VAR模型的脈沖響應函數并進行相應分析；

（7）基于VAR模型引入VEC模型探究變量之間的短期波動和長期均衡。

2 實證

2.1 數據來源

本文數據來源于東方財富網（http://data.eastmoney.com/cjsj/），選取2010年1月至2016年9月的我國消費者信心指數（CCI）和生產價格指數（PPI）月度數據，共有81個時間點，圖1為我國消費者信心指數（CCI）和生產價格指數（PPI）的時間序列圖。

圖1 CCI與PPI的時間序列圖

2.2 序列的平穩性檢驗

從圖1可以看出，CCI序列和PPI序列隨著時間變化而有所變化，從直觀上判斷可知CCI序列和PPI序列具有明顯的非平穩性。需要對序列進行單位根檢驗以判斷其平穩性。為消除季節趨勢和異方差性、減少波動，對序列CCI、序列PPI分別取對數，記為序列LNCCI和序列LNPPI。再對兩組對數序列進行一階差分，生成的序列分別記為序列DLNCCI和DLNPPI，并對兩序列進行單位根檢驗。

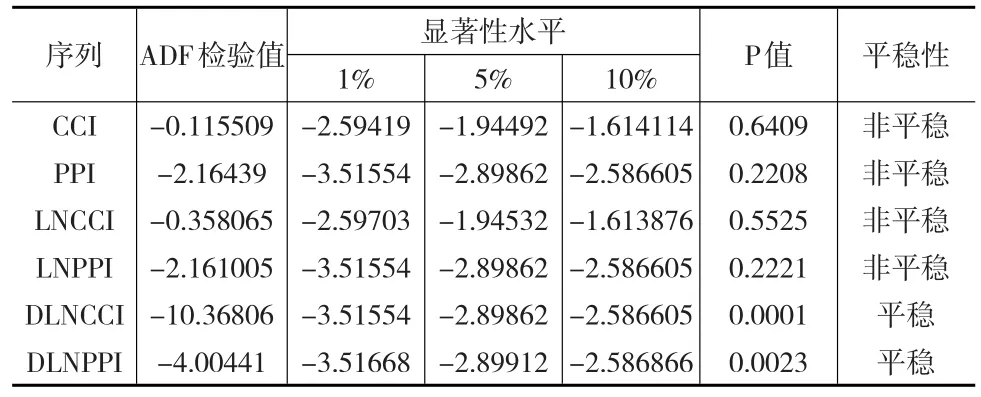
表1 兩序列的單位根檢驗結果

由表1可知，原始序列CCI、PPI、LNCCI和LNPPI的ADF檢驗值均大于檢驗水平為1%、5%和10%的t統計量臨界值，同時概率P值均大于0.05，因此不拒絕原假設，即認為原始序列CCI、PPI、LNCCI和LNPPI是非平穩序列。經過差分后的序列DLNCCI和DLNPPI，ADF檢驗值均小于t統計量臨界值，同時概率P值均小于0.05，因此，可以認為序列DLNCCI和DLNPPI為平穩序列。序列LNCCI和LNPPI都是一階單整序列，說明兩者之間可能存在著長期的協整關系。

2.3 VAR模型最大滯后階數的確定

在構建VAR模型之前，可以依據赤池信息準則（AIC）和施瓦茨（SC）準則來確定模型的最大滯后階數p，結果如表2所示。

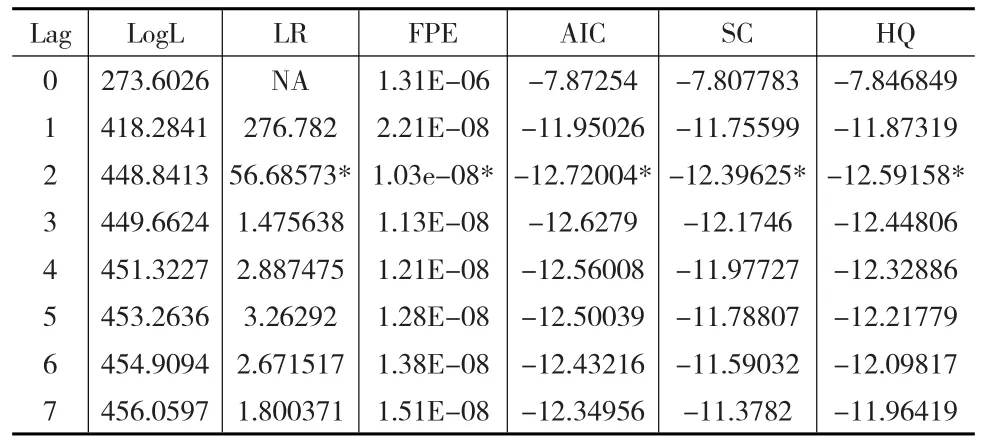
表2 最大滯后階數選擇準則

從表2可看出，AIC和SC最小值對應的階數p均為2，故VAR模型選擇滯后階數p=2為最大滯后階數。

2.4 VAR模型的建立和檢驗

根據前面的已知條件，所建立的VAR（2）模型可寫成矩陣形式（5）：

VAR（2）模型的AIC值為-12.56607，SC值為-12.26614，AIC和SC值都很小，說明所建立的VAR（2）模型效果較好。為了檢驗VAR模型的平穩性，本文選擇使用AR根的圖表驗證。從圖2可以很直觀地看出，所有單位根的倒數的模都落在了單位圓之內，因此，所建立的VAR（2）模型是穩定的。

2.5 Johansen協整檢驗

序列為非平穩序列時，構建模型很可能出現偽回歸。協整檢驗的目的就是檢驗回歸方程所描述的因果關系是否是偽回歸，即檢驗變量之間是否存在長期穩定的關系。協整檢驗要求各序列是非平穩序列，并且是同階單整序列。從單位根檢驗結果可以知道，序列LNCCI和LNPPI滿足協整檢驗的要求。

圖2 AR單位根的分布圖

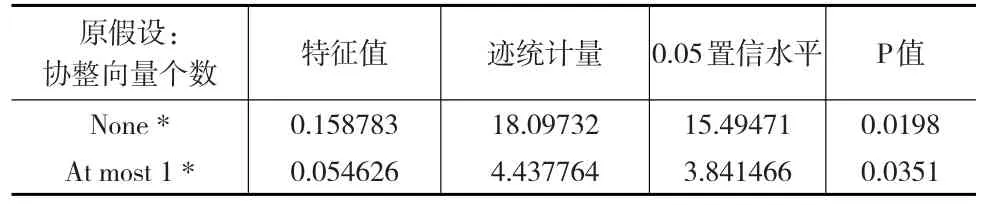
表3 Johansen協整檢驗結果

從表3可知，在5%的置信水平下，特征值和跡統計量檢驗值均大于臨界值，第一行、第二行P值分別為0.0198和0.0351，均小于0.05，拒絕了不存在協整關系的原假設，即說明消費者信心指數與生產價格指數之間存在長期協整關系。經過標準化協整系數后，所得到的協整方程如下式（6）所示：

2.6 脈沖響應函數分析

為了描述在隨機誤差項上施加一個標準差大小的沖擊對變量的當前值和未來值所產生的影響大小，本文采用脈沖響應函數分析我國消費者信心指數與生產價格指數的響應情況。

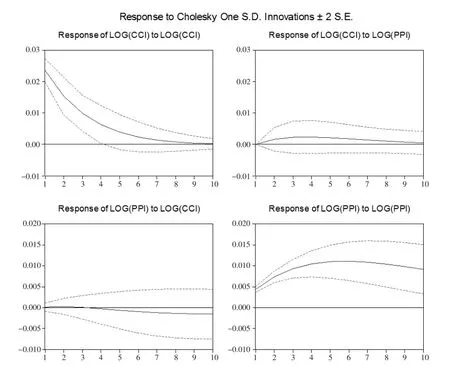
圖3 脈沖響應函數合成圖

由圖3的脈沖響應結果可知，我國消費者信心指數對自身的沖擊響應，第1期達到了最大值0.023575，隨后開始下降直到趨向于0，由此可見，我國消費者信心指數對自身存在著短期的干擾，但是從長遠來看，消費者信心指數對自身的影響作用很小，幾乎不受自身影響。我國消費者信心指數對生產價格指數第1期沒有立即做出反應，隨著滯后期的延長開始上升，第4期上升到最高點0.002356后逐漸下降近趨向于0，因此，無論從長期還是短期來看，雖然消費者信心指數對生產價格指數會產生一定的沖擊，但是影響作用不大。

生產價格指數第1期開始就對自身的沖擊響應，第6期達到最大值0.011073，隨后開始下降但不為0，說明生產價格指數對自身有著一定的長期影響。生產價格指數對我國消費者信心指數有著一定的影響，前3期對消費者信心指數產生沖擊力很小的正向作用，但是到第4期開始做出負向反應，并且長期趨向于-0.002，因此，雖然生產價格指數對我國消費者信心指數沒有立即做出響應，開始呈現正向影響，但是從長期趨勢來看，生產價格指數對我國消費者信心指數有著長期的負向影響。當生產價格指數增加時，消費者對經濟走勢信心會有所下降。

2.7 VEC模型建立和參數估計

由Johansen協整檢驗可知，消費者信心指數與生產價格指數之間存在著長期的協整關系。基于前面的VAR（2）模型可以建立VEC模型分析兩者之間的長期穩定關系以及短期波動情況。

VEC模型：

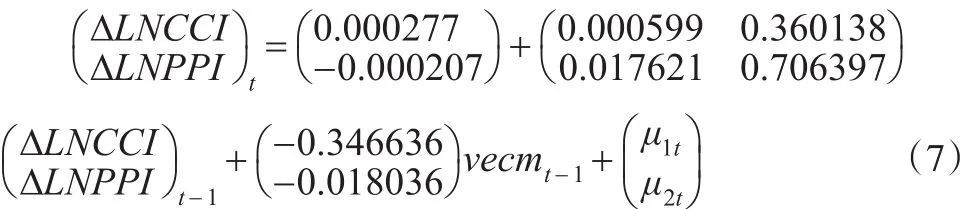
其中，協整方程vecmt-1：

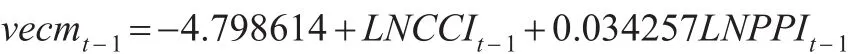
從VEC模型的估計結果可知，模型中的AIC值為-12.5099，SC值為-12.20997，兩個值都較小，說明VEC模型是非常合理的。從式（7）可以看出，前一期的CCI和PPI對本期的CCI有著正向作用，且PPIt-1影響最大，說明上一期的生產價格指數上漲，會增強本期的消費者信心指數。在長期均衡關系中，CCI和PPI每增加一個百分點，下一期的CCI分別增加0.000599、0.360138個百分點。VECM是誤差修正項，其系數是負值，說明CCI以0.346636的值反向修正下一期的CCI值以到達一個長期均衡的狀態。生產價格指數適當增大有利于提高消費者信心指數，有利于促進社會經濟穩定發展。

圖4是變量CCI和PPI之間的協整關系曲線，從整體上看，從2010年到2013年底和2015年，尤其是2011年底和2013年，誤差修正項的絕對值偏離較大，也就是說短期波動偏離了長期均衡。2014年開始，誤差修正項的波動幅度開始變小，逐漸回到長期均衡的狀態。

3 結論

本文運用VAR-VEC組合模型對我國消費者信心指數和生產價格指數進行實證分析，研究了CCI和PPI之間的協整關系，得到以下結論：

圖4 LNCCI和LNPPI的協整關系圖

（1）LNCCI序列和LNPPI序列經過一階差分后達到平穩，都屬于一階單整序列。利用兩序列滯后2期高度顯著，構建VAR（2）模型，說明了當期的消費者信心指數和生產價格指數會受到前2期的變化影響。

（2）LNCCI和LNPPI之間存在協整關系，表明消費者信心指數與生產價格指數之間存在長期穩定的關系。

（3）LNCCI和LNPPI的脈沖響應情況表明CCI對自身有短期波動的影響，幾乎不存在長期影響；無論是從短期波動，還是長期影響來看，CCI對PPI都產生一定的沖擊影響，但是沖擊力度不大。PPI對自身存在一定的影響，對CCI存在長期負向影響。

（4）VEC模型分析了CCI和PPI之間的長期穩定關系以及短期波動情況，當期的CCI、PPI都會受到前一期的CCI和PPI正向影響。誤差修正項系數是負值，起到反向修正下一期CCI、PPI值以達到長期均衡狀態的作用。

[1]張曉帥，姚儉.運用改進灰色模型預測消費者信心指數[J].統計與決策，2012，（19）.

[2]徐婷.時間序列模型在消費者信心指數預測中的應用[D].大連：遼寧師范大學學位論文，2013.

[3]董大勇，劉珂言.基于ARIMA模型的工業品出廠價格指數預測與分析[J].統計與決策，2016，（1）.

[4]趙永興，孫高潔.基于EGARCH模型的我國工業品出廠價格指數（PPI）波動的實證研究[J].市場經濟與價格，2013，（3）.

[5]何毅，王新.消費者信心指數對CPI的影響效應探討[J].價格理論與實踐，2012，（12）.

[6]李躍輝，彭嘉瑩.基于VAR-VEC模型的物價指數關系研究[J].統計與決策，2012，（15）.

[7]何躍，侯婧.生產價格指數對宏觀經濟預警與實證[J].統計與決策，2016，（20）.

[8]Sims C A.Macroeconomics and Reality[J].Econometrica，1980，(48).

[9]Johansen S，Juselius K.Maximum Likelihood Estimation and Inferences on Cointegration-with Applications to the Demand for Money[J].Oxford Bulletin of Economics and Statistics，1990，(52).

[10]高鐵梅.計量經濟分析方法與建模——EViews應用及實例[M].北京：清華大學出版社，2009.