基于“情境串”的概念教學
——《平均數》教學案例（二）

沈曉鈺

【教學內容】

人教版四年級下冊第90～92頁。

【教學過程】

一、創(chuàng)設情境，初步感知

1.談話引入。

師：大家最喜歡的體育運動是什么？

生：籃球、羽毛球……

師：老師最喜歡踢毽子。就在上星期，班上的小紅、小麗和小娟同學還和我進行了一場踢毽子比賽。想不想了解當時的比賽情況？

【思考：在這里，課堂呈現(xiàn)了“師生踢毽比賽”的現(xiàn)實情境，貼近學生的日常生活，有利于充分調動學生的學習興趣及主體經驗。】

2.體會“移多補少”。

師：首先出場的是小紅，她踢了18個。可是，她對這個成績不太滿意，想再踢兩次。小紅后兩次的踢毽成績很有趣，請看！（課件出示：18個，18個）要表示小紅一次踢毽的個數，用哪個數比較合適？

生：18，因為她每次都踢18個。

師：有道理！接著，該小麗出場了。請看！（課件出示：16個）請看她后兩次的成績。（課件出示：17個，18個）三次成績各不相同，該用哪個數來表示小麗踢毽子的水平呢？

生：用18來表示，因為她最多踢了18個。

生：我不同意。另外兩次都不到18個，怎么能用18來表示她的真實水平呢？

師：也就是說，如果也用18來表示，對小紅來說——

生：不公平！

師：那么應該用哪個數來表示呢？

生：可以用17表示。因為16、17、18三個數，17正好在中間，最能代表她的成績。

生：一次比17多1，一次比17少1，所以整體上可以用17表示。

生：還可以這樣想，把18里多的1送給16，這樣三次就都相當于17個了。

（課件演示：“移多補少”的過程）

師：像這樣，從多的里移一些補給少的，使得每個數都一樣多，這個過程叫“移多補少”（板書）。

【思考：在上述環(huán)節(jié)中，貫穿其間的核心問題是“用哪個數來代表小紅（小麗）踢毽子的水平呢？”。而且，小紅踢毽水平的代表數是在“三個相同的數”中提取的，小麗踢毽水平的代表數是在“三個不同的數”中提取的。這樣的設計，為“移多補少”的策略生成做好鋪墊，也為學生理解“平均數代表整組數據的一般水平”埋下伏筆。】

3.揭示“平均數”。

師：輪到小娟了。她也踢了三次，成績各不相同。（課件出示：16個，15個，20個）該用什么數來代表她踢毽的一般水平呢？先自己思考，再同桌交流。

生：可以用17來代表她的踢毽水平。她第三次踢了20個，可以移1個給第一次，再移2個給第二次，這樣每次看起來好像都踢了17個。

（課件演示：“移多補少”的過程）

師：還有別的想法嗎？

生：我們可以先把小娟三次踢毽的個數相加，是51個。再用51除以3等于17個。（教師板書：16+15+20=51，51÷3=17）

師：這種“求和平分”的方法，能使每次看起來一樣多嗎？

生：能！都是17個。

師：其實，無論是“移多補少”，還是“求和平分”，目的只有一個，那就是——

生：使原來幾個不相同的數變得相同。

師：數學上，我們把通過“移多補少”或“求和平分”得到的這個“同樣多”的數，叫做原來這幾個數的“平均數”（板書課題）。比如，17是 16、17、18的平均數，17是16、20、15的平均數。這里的平均數17，是小娟第一、二、三次踢毽的個數嗎？

生：不是。

師：奇怪，平均數17不是小娟三次踢毽的具體個數，那它究竟表示什么呢？

生：表示的是小娟三次踢毽的一般水平。（板書：一般水平）

【思考：小娟踢毽水平的代表數依然是在“三個不同的數”中提取的。并且，這三個數之間的差異更大。這使得，“移多補少”策略更具挑戰(zhàn)性，“求和平分”方法有了生成的必要。之后，教師還對“平均數17究竟表示什么”作出了追問與提點，有力促進了全體學生對“平均數”意義的理解。】

二、延續(xù)情境，深化感受

1.想一想，選一選。

師：最后，該老師出場了。（課件出示：18個、17個、19個）老師輸了還是贏了？

生：與小紅打平。與小麗、小娟比，贏了。

師：老師和小紅沒有分出勝負，又踢了一次，（課件出示：14個）現(xiàn)在，老師是輸了還是贏了？

生：輸了。第四次14個不到18個，所以平均數肯定比18小，比不過小紅。

師：有道理。與成績最好的小紅比，老師輸了；那與其他兩位同學比，結果又怎樣呢？（列式計算，交流過程：18+17+19+14=68，68÷4=17）

師：假如老師第四次踢了18個或22個。大家覺得“18、17、19、18”和“18、17、19、22”這兩組數據分別用哪種方法找平均數比較合適？為什么？

生：第一組移多補少。很方便，一眼就看出來了。

生：第二組求和平分。18+17+19+22=76，76÷4=19。

師：看來，尋找平均數時，要選擇合適的方法。

【思考：通過情境鋪展，讓學生徹底融入其中，確保了參與度。整個過程中，教師有意識地組織學生進行直觀分析，培養(yǎng)了數感和數據分析能力。之后，通過兩組數據得出平均數的方法比較，突出了解決策略的選擇性與優(yōu)化。】

2.看一看，說一說。

師：請大家觀察這三幅圖，有什么發(fā)現(xiàn)？

生：我發(fā)現(xiàn)，每一幅圖中，前三次成績不變，而最后一次成績各不相同，所以平均數也不同。

師：難怪有人說，平均數這東西很敏感，任何一個數據的變化，都會使平均數發(fā)生變化。（板書：隨任意一個數的變化而變化）

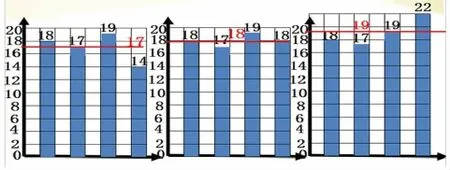
生：我發(fā)現(xiàn)平均數比最大的數小、比最小的數大。

師：能解釋一下為什么嗎?

生：很簡單。多的要移一些補給少的，最后的平均數當然比最大的小，比最小的大。

師：課后，同學們可以繼續(xù)研究。或許，你們會有更多的發(fā)現(xiàn)！

【思考：通過對前段教學中出現(xiàn)的三組數據信息的匯總觀察與線索梳理，有利于學生對平均數的本質特點建立更全面、更完整的主體感悟。】

三、豐富情境，促進感悟

1.基礎訓練。

師：上星期，我們班五位男生組成的男生隊和四位女生組成的女生隊比賽。（課件出示教材第91頁表格）

師：如果要你判斷哪個隊伍的成績好些，你會根據什么來判斷？

生：平均數。

師：為什么不用總數來判斷呢？

生：人數不同，不公平。

師：不計算，你能來估一估這兩個隊伍的平均成績嗎？估好后，請大家選擇合適的方法來算算，驗證你估計的到底對不對。

【思考：該題來源于課本例題，但又很好地與本課主題情境融合在一起。通過想一想、估一估、算一算，學生的數據分析能力再度得以歷練。】

2.變式訓練。

（1）（課件出示教材練習二十二第5題）這是蛋糕店的草莓蛋糕最近5天的銷售情況。糕點師傅明天做多少個草莓蛋糕才合適呢？

（2）據《2015年世界衛(wèi)生報告》：“目前中國女性的平均壽命大約是76歲。”有一位75歲的老奶奶知道這個消息后非常難過。你知道是為什么嗎？你能運用今天所學的知識來勸勸老奶奶嗎？

【思考：兩道變式訓練的設計，著眼日常生活中的平均數現(xiàn)象，致力于引導學生應用所學知識、解決實際問題，強化其實踐觀念與應用意識。】