基于改進均值回歸的波羅的海原油運價指數(shù)模型研究

馮文文, 匡海波, 孟 斌

(大連海事大學(xué)綜合交通運輸協(xié)同創(chuàng)新中心，遼寧 大連 116026)

1 引言

眾所周知，原油市場變化多端，給原油運輸和相關(guān)企業(yè)的經(jīng)營、決策帶來了很大困難。關(guān)于原油市場分布、波動特征以及風險管理的研究越來越受到原油運輸企業(yè)管理者、研究者和投資者的重視。油輪運價指數(shù)波動作為油輪運輸市場變化趨勢的“陰晴表”，也受到航運界經(jīng)營者廣泛關(guān)注。有效地掌握國際原油運價指數(shù)的波動規(guī)律及變化特征對油輪運輸投資和經(jīng)營者制定投資決策、把握市場動態(tài)有著至關(guān)重要的意義，并且對國家準確制定相關(guān)策略和企業(yè)規(guī)避相關(guān)海運風險起著非常重要的作用。

最早開始研究油輪市場運價指數(shù)波動特征方面的專家學(xué)者是Koopmans[1]，早在1939年，就從市場供求關(guān)系角度出發(fā)，加上經(jīng)濟學(xué)理論方法，得出了市場運價彈性在運力相對少的情況下較高的結(jié)論，自此，油輪運價指數(shù)波動性的研究成為航運經(jīng)濟研究的焦點。現(xiàn)行研究和預(yù)測航運運費價格大多是基于隨機過程和經(jīng)濟學(xué)擴展模型進行的，其中，運用隨機過程方法研究油輪運輸?shù)睦佑泻芏唷＠纾珹dland和Cullinane[2]利用非參數(shù)馬爾可夫擴散法研究即期油輪運價的波動性，認為非線性隨機模型最能描述運價的波動特性。Poblacion[3]研究了運費率的隨機季節(jié)性波動行為，其結(jié)果表明運費在冬季和春季比較高且這些差異是不確定的，具有隨機性。Abouarghoub等[4]基于馬爾科夫轉(zhuǎn)換對油輪運輸市場的風險及波動性進行研究。實證研究結(jié)果表明，油輪運費波動是集群出現(xiàn)的，這表明波動有可能在不同國家之間進行切換。Batchelor等[5]通過研究不同時間序列模型對主要海運貨運航線的即期和遠期利率的預(yù)測性能，發(fā)現(xiàn)向量平衡修正模型的樣本擬合度最高，預(yù)測準確度較低。同樣，運用經(jīng)濟學(xué)方法研究油輪運輸?shù)睦右灿泻芏唷＠纾篋robet等[6]通過運用GARCH-X模型和EGARCH模型對干散貨、油輪運輸市場的動態(tài)時變波動進行了研究。其結(jié)果顯示雖然干散貨運費市場沒有受到不對稱性的影響，但油輪運輸市場影響強烈。Sun Xiaolei等[7]從多尺度相關(guān)性的角度對油輪運費和石油價格之間的動態(tài)關(guān)系進行識別。實證結(jié)果表明，油輪運費和油價表現(xiàn)出不同的多尺度特性且兩者在中期和長期具有顯著的相關(guān)性。Zhu Chunying和Ren Xianling[8]研究了金融危機以后原油運費與未來原油價格之間的關(guān)系，結(jié)果表明在經(jīng)濟波動時，油輪運價與原油期貨價格之間不存在長期均衡關(guān)系，二者價格主要受投機等偶然因素的影響；經(jīng)濟平穩(wěn)時，二者價格波動存在長期均衡關(guān)系，原油期貨價格是油輪運價波動的因素之一。其他方法包括：Ji Mingjun等[9]運用組合模型對油輪運價指數(shù)進行了分析與預(yù)測，根據(jù)油輪運價指數(shù)的自身非線性變化趨勢，建立了三層 BP神經(jīng)網(wǎng)絡(luò)模型預(yù)測油輪運價指數(shù)的發(fā)展趨勢。Fan Shuangrui等[10]通過運用小波神經(jīng)網(wǎng)絡(luò)對波羅的海原油運價指數(shù)進行預(yù)測。Eslami等[11]運用簡潔的變量和自適應(yīng)的混合人工神經(jīng)網(wǎng)絡(luò)遺傳算法對原油運費進行了預(yù)測，其結(jié)果不僅顯著優(yōu)于回歸方法和移動平均方法，甚至略優(yōu)于現(xiàn)有研究的結(jié)果。Zhang Jiao和Zeng Qingcheng[12]基于改進的經(jīng)驗?zāi)B(tài)分解研究油輪運費市場的波動性，結(jié)果表明，雖然原始運費系列之間的波動溢出效應(yīng)并不顯著，但分解重組后結(jié)果具有一定的波動溢出效應(yīng)。

以上專家分別從時間序列及市場需求、產(chǎn)出等角度運用不同方法對航運價格指數(shù)的波動特性進行了研究。但是，作為金融衍生品的一種，航運價格指數(shù)的波動應(yīng)該符合金融衍生品的經(jīng)濟學(xué)特性，其價格應(yīng)該圍繞價值上下波動，且最終會隨著市場供需比例的調(diào)整而回到一個定值[13]，即航運價格指數(shù)應(yīng)具有“均值回歸”的特性。

均值回歸理論作為金融市場可預(yù)測理論的一個突破性進展，長期以來，是金融市場研究的熱點，被廣泛應(yīng)用于股票投資、證券分析等領(lǐng)域[14-15]。但是研究發(fā)現(xiàn)，金融及證券領(lǐng)域?qū)祷貧w理論的應(yīng)用大多都是建立在均值水平為一個定值的前提下的，并沒有考慮在現(xiàn)實經(jīng)濟活動中，均值水平受其他因素影響隨時間的變動，且人們對于均值回歸理論的研究更側(cè)重于對其特性的證明和驗證，具體的關(guān)于均值回歸的樣本路徑及針對路徑趨勢的預(yù)測分析不足。例如，Kou Ying和Luo Meifeng[16]雖然在探討船價和運輸價格之間的關(guān)系的構(gòu)成中，運用了擴展的均值回歸過程的假設(shè)，但是其并沒有驗證運費的均值回歸性假設(shè)的合理性。Taib[17]雖然在運用即期對遠期的關(guān)系框架推導(dǎo)出遠期運費合同的價格時基于包含均值回歸的六種不同隨機過程的定價，但是沒有對具體的回歸過程的路徑進行擬合。

針對現(xiàn)有研究的不足，本文在傳統(tǒng)均值回歸模型的基礎(chǔ)上，通過引入均值隨時間變化的一元回歸方程，構(gòu)建了改進的均值回歸模型，并推導(dǎo)求解出該改進均值回歸模型的預(yù)測模型及置信區(qū)間。進而利用改進后的均值回歸模型對原油運價指數(shù)的樣本路徑進行分析，預(yù)測原油運價指數(shù)的波動趨勢和變化規(guī)律。通過對比改進前后均值回歸模型的擬合效果可以看出，該模型提高了傳統(tǒng)均值回歸模型的擬合精度，降低了模型的預(yù)測誤差。本文其余部分的結(jié)構(gòu)安排如下：第2部分為科學(xué)問題的性質(zhì)及難點；第3部分為改進均值回歸模型的方法介紹；第4部分為具體的實證分析；第5部分為結(jié)論。

2 科學(xué)問題的性質(zhì)及難點

2.1 科學(xué)問題的性質(zhì)

原油運價指數(shù)的分析預(yù)測就是通過對歷史數(shù)據(jù)的處理，分析構(gòu)建能夠反映樣本特性的模型，得到代表樣本運行趨勢的擬合曲線，揭示原油運價指數(shù)的運行規(guī)律，為航運市場參與者規(guī)避風險、做出決策提供依據(jù)。

2.2 問題的難點

難點一：如何根據(jù)數(shù)據(jù)特性合理的建立預(yù)測模型。特性不同，對應(yīng)的模型不同。模型選取恰當與否，決定預(yù)測準確度的高低。若模型選取不恰當，有可能導(dǎo)致數(shù)據(jù)趨勢判斷誤差加大，預(yù)測準確度降低。

難點二：如何基于建立的模型進行求解，得到參數(shù)的估計值，從而對模型的有效性及準確度進行評價。模型能否得到可行解是模型建立最基本的要素之一，若模型無法得到合適的解，模型的建立將沒有意義。

2.3 突破難點的思路

難點一的解決思路：基于特性檢驗，建立“均值水平”隨時間變動的均值回歸模型，體現(xiàn)原油運價指數(shù)均值隨時間變化的特征；運用模型對原油運價指數(shù)進行擬合，通過與其他擬合模型的比較，表明擬合的顯著性。

難點二的解決思路：首先，基于柯爾莫哥洛夫前向方程，運用概率密度函數(shù)及矩母函數(shù)性質(zhì)得到偏微分方程的解，從而計算推導(dǎo)出預(yù)測模型的函數(shù)表達式；其次，運用一元自回歸模型及鞅函數(shù)定理求得模型的參數(shù)估計，從而得到建立模型的數(shù)值解，對模型效果進行分析。

2.4 基于改進均值回歸模型的波羅的海原油運價指數(shù)分析預(yù)測的步驟

(1)分別運用單位根及方差比率檢驗對數(shù)據(jù)的均值回歸特性進行檢驗。

(2)依據(jù)油輪運價指數(shù)均值隨時間變動的特性建立新的改進的均值回歸模型。

(3)依據(jù)柯爾莫哥洛夫前向方程，運用概率密度函數(shù)及矩母函數(shù)性質(zhì)得到基于改進均值回歸模型的預(yù)測模型。

(4)依據(jù)一元自回歸過程及文獻[21]中相關(guān)定理求解未知參數(shù)，得出擬合方程。

(5)比較改進模型及經(jīng)典模型預(yù)測值與實際值的大小，并對其進行分析。

(6)計算改進模型與經(jīng)典模型的預(yù)測值和實際值的擬合優(yōu)度R，并進行對比分析，驗證改進方程擬合結(jié)果的優(yōu)勢及合理性。

3 基于改進均值回歸模型的構(gòu)建

3.1 均值回歸檢驗方法

均值回歸理論認為，金融資產(chǎn)的價格無論低于或高于均值水平，長期看都會以很高的概率向均值回歸。基于計量經(jīng)濟學(xué)理論，本文擬采用單位根檢驗及方差比率檢驗方法對其歷史數(shù)據(jù)的均值回歸性進行實證檢驗。

(1)單位根檢驗

單位根檢驗的目的：檢驗時間序列是否平穩(wěn)，為進行均值回歸打下基礎(chǔ)。

單位根檢驗的思路：通過驗證序列是否存在單位根來確定數(shù)列的平穩(wěn)性，從而判定該序列是否滿足均值回歸特性。若存在單位根，說明時間序列不平穩(wěn)，不可以進行均值回歸計算；反之，說明時間序列平穩(wěn)，可以進行均值回歸的計算。在一定的顯著性水平下，如果單位根檢驗的統(tǒng)計量小于該顯著性水平下的臨界值，則認為序列滿足均值回歸特性；反之，不滿足。

(2)方差比率檢驗

對時間序列方差比率的檢驗是從長期價格方差與短期價格方差的比的角度驗證數(shù)據(jù)均值回歸特性的方法。

方差比率檢驗的思路：通過方差比率檢驗，確定短期價格的自相關(guān)性，從而確定短期價格是否過度波動，長期序列是否呈均值回歸過程。即如果VR(k)<1，則表示短期價格序列存在負的自相關(guān)，說明短期價格過度波動，長期序列呈均值回歸；如果VR(k)>1，則為均值回避；若VR(k)=1，則市場有效，價格隨機波動，不存在自相關(guān)。

3.2 改進均值回歸模型的建立

3.2.1 樣本路徑模型

均值回歸是一種通常用于股票投資，證券分析的數(shù)學(xué)方法。其基本思想是商品及金融衍生品的價格總是在圍繞價值上下波動，且最終會隨著市場供需比例的調(diào)整而回到一個定值[18]。當現(xiàn)在市場價格低于前一段時間的平均價格時，價格將上升；同理，當現(xiàn)在的市場價格高于前一段時間的平均價格時，價格將下降，最終通過價格的不斷波動，將會達到一個“平均水平”。近年來人們針對均值回歸理論進行了大量的研究，包括均值回歸的檢驗[19-22]、均值回歸在證券及股票市場的應(yīng)用[23]等，甚至基于均值回歸特性做了大量關(guān)于投資決策[24-26]的研究。

原油運價指數(shù)的均值回歸從理論上講應(yīng)具有必然性。一方面，從長期來看，原油運價市場應(yīng)該服從價值規(guī)律。另一方面，航運市場是一個相對自由的市場，船東可以自由的進出市場，因此價值規(guī)律在航運市場中起到重要作用，即航運市場供求關(guān)系的變化會引起海運價格的變化，而海運價格的變化又會反過來引起航運市場供求關(guān)系的變化，兩者是相互影響、相互作用的。

根據(jù)文獻[13]，得到傳統(tǒng)的均值回歸模型：

(1)

(2)

式(2)的經(jīng)濟學(xué)含義：通過原油運價指數(shù)的歷史數(shù)據(jù)擬合式(2)中的待估參數(shù)a0,a1,η及σ，為以后預(yù)測打下基礎(chǔ)。

3.2.2 預(yù)測模型

均值回歸就是基于價格向均值回歸的特性，利用歷史數(shù)據(jù)對將來價格進行預(yù)測的一種方法。本文在分析傳統(tǒng)均值回歸過程的模型的基礎(chǔ)上，推導(dǎo)得到改進的均值回歸模型的預(yù)測模型，并給出了相應(yīng)的置信區(qū)間。

為了推導(dǎo)出基于改進均值回歸模型(2)的預(yù)測模型，首先需要簡要介紹一下柯爾莫哥洛夫前向方程及矩母函數(shù)。

(1)柯爾莫哥洛夫前向方程

柯爾莫哥洛夫前向方程描述了概率密度φ(x0,t0;x,t)隨時間的演變情形。因此，想要得到一般伊藤過程x(t)(x(t)滿足dx=a(x,t)dt+b(x,t)dz)的柯爾莫哥洛夫前向方程需要應(yīng)用概率密度函數(shù)進行推導(dǎo)。令φ(x0,t0;x,t)表示x(t)的概率密度函數(shù)，給定較早時間t0，有x(t0)=x0，這樣：

(3)

參考Dixit和Pindyck[13]分別對φ(x0,t0;x-Δh,t-Δh)與φ(x0,t0;x+Δh,t-Δh)進行泰勒級數(shù)展開，整理得到柯爾莫哥洛夫前向方程：

(4)

(2)矩母函數(shù)

在統(tǒng)計學(xué)中，矩又被稱為動差。矩母函數(shù)又被稱為動差生成函數(shù)。 隨機變量x(t)的矩母函數(shù)的定義為：

(5)

且對于M(θ,t)，我們有M′=E(x)，Mk=E(xk)。

因此，運用柯爾莫哥洛夫前向方程及矩母函數(shù)，假設(shè)t0=0，改進的均值回歸模型(2)的預(yù)測模型的推導(dǎo)過程如下：

化簡整理式(2)，我們可以得到：

(6)

從而，式(2)的柯爾莫哥洛夫向前方程為：

(7)

又由于x(t)的矩母函數(shù)得：

(8)

(9)

由概率密度函數(shù)及矩母函數(shù)性質(zhì)可知此偏微分方程的邊界條件：

(10)

從而可以得到M(θ,t)解的一種形式為

(11)

其中，

(12)

從而得到：

(13)

因此，由矩母函數(shù)性質(zhì)得：

E(xt)=-Mθ(0,t)=[a(t+t0)+b]C0-e-ηtC1

(14)

2(at+b)e-ηtC1+2e-2ηtC2

(15)

因此，得：

(16)

從而求得改進方程中x在未來任一時間t的期望與方差分別為：

(17)

(18)

式(17)的意義為：當x的當前值為x0，x(t)服從式(2)時，x在未來任一時間t的期望值。即，改進的均值回歸模型所對應(yīng)的預(yù)測模型。

又由統(tǒng)計學(xué)理論，假設(shè)x∈[E(x)-ε,E(x)+ε]且x～N(E(x),Var(x))，可知，

(19)

設(shè)

(20)

則在時間t處，置信水平為α的置信區(qū)間為

(21)

對比文獻[13]中傳統(tǒng)均值回歸模型的期望與方差：

(22)

(23)

3.3 參數(shù)估計方法

(1)方差的瞬時變動率σ的估計方法

假定我們所取得數(shù)據(jù)為等間隔的(由于截取的為周數(shù)據(jù)，故等間隔的假定是合理的)，于是得到觀測時間序列{xt1,xt2,…,xtn}。為了簡化符號，記xt=xti(1≤t≤N)，則可設(shè)等距離間隔dxt=xt-xt-1，dt=1。因此，由式(2)得:

(24)

從而得式(2)離散形式：

(25)

其中，εt-1服從標準正態(tài)分布。

合并同類項得：

(26)

(27)

(28)

得出σ的估計值。

(2)均值回歸速度η的估計方法

基于Bibby[21]所給出的相關(guān)定理：若,

dxt=b(xt,η)dt+σ(xt,η)dz

(29)

那么當且僅當其如下鞅函數(shù)為0時

(30)

可以得到常數(shù)η的無偏估計，其中

(31)

利用該定理，η的有效估計可由下式得到：

(32)

另外，由常微分方程(2)在區(qū)間t-1到t的解為：

(33)

因此

(34)

(35)

整理得均值回歸速度η估計值的表達式如下：

(36)

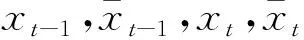
3.4 精度檢驗方法

(1)擬合優(yōu)度R的判定

擬合優(yōu)度R的判定的目的：通過求解擬合優(yōu)度R的值，判定模型的擬合程度。擬合優(yōu)度是一個統(tǒng)計術(shù)語，是用來衡量金融模型的預(yù)期值和現(xiàn)實所得的實際值差距的方法。計算公式如下：

R=

(37)

其中，R∈[0,1]。R越接近于1，表明模型的擬合程度就越高。反之，路徑擬合程度越低。

(2)平均相對誤差的判定

平均相對誤差判定的目的：通過計算平均誤差，測得預(yù)測值與實際值的偏離。相對誤差是絕對誤差與測量值或多次測量的平均值的比值。平均相對誤差是相對誤差的平均值，其計算公式如下：

(38)

Mean-Error≥0。Mean-Error的值越小，路徑的擬合結(jié)果與原數(shù)據(jù)誤差越小。反之，擬合結(jié)果越大。

4 基于改進均值回歸模型的實證分析

4.1 數(shù)據(jù)選取

波羅的海原油運價指數(shù)(Baltic Dirty Tanker Index，BDTI)由波羅的海證券交易所統(tǒng)計，是反應(yīng)國際油輪運輸市場走勢的晴雨表，也是反應(yīng)國際貿(mào)易情況的領(lǐng)先指標之一，探討其波動規(guī)律具有重要意義。因此，本文選取克拉克森所發(fā)布的波羅的海原油運價指數(shù)為數(shù)據(jù)來源，樣本區(qū)間為2010年1月到2016年12月共361個數(shù)據(jù)點，如圖1。

圖1 BDTI指數(shù)

4.2 數(shù)據(jù)特性檢驗

首先，對數(shù)據(jù)進行基本的統(tǒng)計分析，得其均值為776.2433，標準差為129.5599，波峰為1287.2，波谷為578.8，總體看來數(shù)據(jù)波動比較平緩，沒有太多劇烈起伏。

其次，對數(shù)據(jù)分別進行ADF檢驗及方差比率檢驗，驗證數(shù)據(jù)的均值回歸特性，結(jié)果如表1、表2所示。從表1中可以看出，ADF統(tǒng)計量-5.3589顯著小于1%水平下的臨界值-3.4504。因此，原油運價指數(shù)具有顯著的均值回歸的特性。從表2中可以看出，在滯后期大于12周時，方差比VR=0.9830小于1，原油運價指數(shù)存在序列負相關(guān)，符合均值過程特征。

表1 ADF檢驗

表2 方差比檢驗

4.3 改進均值回歸方程的參數(shù)估計

表系數(shù)估計值

從而得到BDTI指數(shù)的均值水平方程為：

(39)

第二，將所取的樣本數(shù)據(jù)帶入式(28)和式(36)，計算改進均值回歸模型的系數(shù)；同時參考Dixit和Pindyck[13]，計算得傳統(tǒng)均值回歸過程的系數(shù)，具體結(jié)果如表4所示：

表4 系數(shù)估計值

第三，基于Drobetz等[6]將估計值分別代入，得到傳統(tǒng)均值回歸的運動方程及其對應(yīng)的期望、方差：

(40)

89.9517]

將估計值分別代入式(2)、(17)、(18)和式(21)得到改進均值回歸的運動方程及其對應(yīng)的期望、方差和置信區(qū)間：

(41)

4.4 模型的對比分析

為了驗證改進模型的預(yù)測顯著性，總體選用2010年1月到2016年12月共361周的波羅的海原油運價指數(shù)(BDTI指數(shù))，運用matlab將不同預(yù)測長度的數(shù)據(jù)均帶入公式(40)及(41)，驗證傳統(tǒng)的均值回歸模型和改進的均值回歸模型對不同預(yù)測長度數(shù)據(jù)的預(yù)測效果。

(1)為了驗證模型的預(yù)測效果，利用傳統(tǒng)的均值回歸模型和改進的均值回歸模型在相同置信水平0.9下分別對2016年10月到2016年12月共計12周(三個月)數(shù)據(jù)的原油運價指數(shù)進行預(yù)測，結(jié)果見圖2及圖3(圖2及圖3左側(cè)圖形為數(shù)據(jù)整體圖，右側(cè)圖形為預(yù)測路徑及預(yù)測區(qū)間的放大圖)，并分別將預(yù)測值與實際值進行比較，比較結(jié)果見表5。

表5 均值可變和均值不變模型預(yù)測誤差

圖2 均值改變過程的預(yù)測

圖3 均值不變過程的預(yù)測

(2)為了評價模型的擬合效果，求解表5中預(yù)測值與實際值的擬合優(yōu)度R及平均相對誤差Mean-Error作為評價指標，結(jié)果見表6。

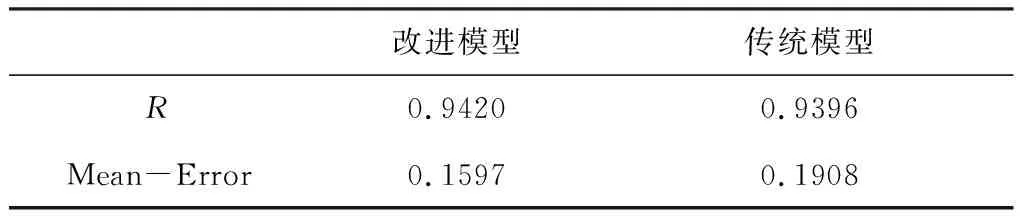
表6 兩種模型的性能比較

(3)為了更進一步顯示模型改進預(yù)測效果，利用2010年1月到2015年12月共309組數(shù)據(jù)對2015年12月到2016年12月共52周(1年)數(shù)據(jù)分別運用兩個模型在相同置信水平0.90下進行預(yù)測，預(yù)測結(jié)果見圖4及圖5。

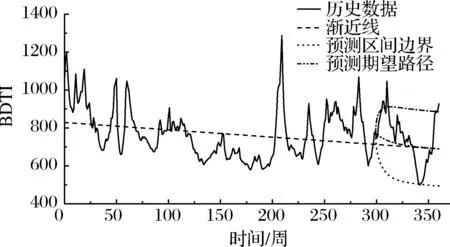
圖4 均值改變過程1年期預(yù)測效果顯示

圖5 均值不變過程1年期預(yù)測效果顯示

通過實驗結(jié)果的對比分析可得如下結(jié)論：

(1)從表5可以看出，改進預(yù)測模型的預(yù)測數(shù)據(jù)與實際數(shù)據(jù)的相對誤差與絕對誤差總是比傳統(tǒng)模型的相對誤差要低。因此，均值改變的預(yù)測模型具有較高的預(yù)測精度，比均值不變的預(yù)測模型更能反映將來原油運價的趨勢。

(2)從表6比較擬合優(yōu)度R可知，均值可變的擬合優(yōu)度0.9420明顯大于均值不變的情況0.0.9396，且平均相對誤差0.1597明顯小于均值不變的情況0.1908，說明均值可變的均值回歸模型路徑擬合效果更好。

(3)分析比較圖2、圖3中的預(yù)測曲線可知，改進模型與傳統(tǒng)模型具有相同的預(yù)測趨勢，兩者均能預(yù)測出實際數(shù)據(jù)的變動趨勢。但是，在相同的置信區(qū)間內(nèi)，改進模型比傳統(tǒng)模型覆蓋更多的數(shù)據(jù)范圍，且預(yù)測趨勢比傳統(tǒng)模型平緩，這與油輪運輸市場雖然短期運價上升，但整體運價水平降低，在正常市場競爭條件下，上升趨勢不會劇烈變動是比較一致的。

(4)分析圖4中的1年期預(yù)測效果曲線可知，原油運價指數(shù)的實際值幾乎全部位于預(yù)測區(qū)間內(nèi)，且以前309組數(shù)據(jù)值進行預(yù)測，雖然運價在短期內(nèi)有上升的趨勢，但長期來看呈現(xiàn)下降的趨勢，這與21世紀以來，隨著世界經(jīng)濟危機加重，航運市場逐漸衰退，運費大幅降低是一致的。

(5)比較圖4及圖5可以看出，無論是通過改進模型還是傳統(tǒng)模型進行預(yù)測油輪運價均具有降低的趨勢。但是，油輪運價指數(shù)在1年期趨勢下其實際值幾乎均位于改進模型的預(yù)測范圍內(nèi)，原始模型在1年期預(yù)測的趨勢下誤差較大，不能很好地預(yù)測實際值。

5 結(jié)語

本文在傳統(tǒng)的均值回歸模型的基礎(chǔ)上，依據(jù)原油運價指數(shù)特性，提出了改進的均值回歸模型。模型考慮到原油運價指數(shù)的均值水平受多種因素影響，不能長期保持一致這一問題，以及考慮到原油運價指數(shù)隨時間變動的特性，提取了原油運價指數(shù)均值變動的線性趨勢，進而依據(jù)相關(guān)定理求解了改進均值變動過程的預(yù)測模型，并對相關(guān)參數(shù)進行了相應(yīng)的估計。最后，經(jīng)過數(shù)值模擬及對比分析表明，改進模型比傳統(tǒng)模型具有明顯優(yōu)勢，其擬合效果和預(yù)測精度得到明顯提高。

參考文獻：

[1] Koopmans T C. Tanker freight rates and tank ship building[M]. Holland: Netherlands Economic Institute, 1939.

[2] Adland R, Cullinane K. The non-linear dynamics of spot freight rates in tanker markets[J]. Transportation Research Part E: Logistics and Transportation Review, 2006, 42(3): 211-224.

[3] Poblacion J. The stochastic seasonal behavior of freight rate dynamics[J]. Maritime Economics & Logistics, 2015, 17(2): 142-162.

[4] Abouarghoub W, Mariscal I, Howells P. Dynamic risk and volatility in tanker shipping markets: A Markov-switching application[C]//Proceedings of The International Association of Maritime Economists (IAME) Conference Proceedings. Marseille, France, July 3-5, 2013.

[5] Batchelor R, Alizadeh A, Visvikis I. Forecasting Spot and Forward Prices in the International Freight Market[J]. International Journal of Forecasting, 2007, 23(1): 107-114.

[6] Drobetz W, Richter T, Wambach M. Dynamics of time-varying volatility in the dry bulk and tanker freight markets[J]. Applied financial economics, 2012, 22(16): 1367-1384.

[7] Sun Xiaolei, Tang Ling, Yang Yuying, et al. Identifying the dynamic relationship between tanker freight rates and oil prices: In the perspective of multiscale relevance[J]. Economic Modelling, 2014, 42: 287-295.

[8] Zhu Chunying, Ren Xianling. Research on the relationship between the tanker freight and the future price of crude oil in the post financial crisis period[J]. Review of Industrial Economics, 2015, 2: 005.

[9] Ji Mingjun, Zhang Haiyan, Wang Qingbin. Analysis and forecasting of the tanker freight rates based on combined forecasting model[J]. Journal of Transportation Systems Engineering and Information Technology, 2012,2(1): 199-204.

[10] Fan Shuangrui, Ji Tingyun, Gordon W, et al. Forecasting Baltic Dirty Tanker Index by applying wavelet neural networks[J]. 2013, 3(1): 68-87.

[11] Eslami P, Jung K, Lee D, et al. Predicting tanker freight rates using parsimonious variables and a hybrid artificial neural network with an adaptive genetic algorithm[J]. Maritime Economics & Logistics, 2017,19(3):538-550.

[12] Zhang Jiao, Zeng Qingcheng. Modelling the volatility of the tanker freight market based on improved empirical mode decomposition[J]. Applied Economics, 2017,49(17):1655-1667.

[13] Dixit A K, Pindyck R S. Investment under uncertainty[M]. Princeton, N J: Princeton University Press, 1994.

[14] 王明亮, 何建敏, 陳百碩, 等. 時變O-U模型在氣溫預(yù)測及氣溫期貨定價中的適應(yīng)性研究——基于北京市1951-2012年的日平均氣溫數(shù)據(jù)[J]. 中國管理科學(xué), 2015, 23(2): 44-49.

[15] 劉志東, 劉雯宇. Lévy過程驅(qū)動的非高斯OU隨機波動模型及其貝葉斯參數(shù)統(tǒng)計推斷方法研究[J]. 中國管理科學(xué), 2015, 23(8): 1-9.

[16] Kou Ying, Luo Meifeng. Modelling the relationship between ship price and freight rate with structural changes[J]. Journal of Transport Economics and Policy (JTEP), 2015, 49(2): 276-294.

[17] Taib C M I C. Forward pricing in the shipping freight market[J]. Japan Journal of Industrial and Applied Mathematics, 2016, 33(1): 3-23.

[18] Kim J, Park J Y. Mean reversion and unit root properties of diffusion models[R]. Working paper, Indiana University, 2013.

[19] 張躍軍, 魏一鳴. 國際碳期貨價格的均值回歸: 基于EU ETS的實證分析[J]. 系統(tǒng)工程理論與實踐, 2011, 31(2): 214-220.

[20] Astorga P. Mean reversion in long-horizon real exchange rates: Evidence from Latin America[J]. Journal of International Money and Finance, 2012, 31(6): 1529-1550.

[21] Nguyen D, Tie Jingzhi, Zhang Qing. An optimal trading rule under a switchable mean-reversion model[J]. Journal of Optimization Theory and Applications, 2014, 161(1): 145-163.

[22] Benth F E, Koekebakker S. Stochastic modeling of Supramax spot and forward freight rates[J]. Maritime Economics & Logistics, 2016,18(4):391-413.

[23] Bibby B M, Sorensen M. Martingale estimation functions for discretely observed diffusion processes[J]. Bernoulli, 1995, 1(1/2): 17-39.

[24] 宋玉臣, 寇俊生. 滬深股市均值回歸的實證檢驗[J]. 金融研究, 2005,(12): 55-61.

[25] Keles D, Genoese M, M?st D, et al. Comparison of extended mean-reversion and time series models for electricity spot price simulation considering negative prices[J]. Energy Economics, 2012, 34(4): 1012-1032.

[26] Campbell J Y, Lo A W C, MacKinlay A C. The econometrics of financial markets[M]. Princeton, N J: Princeton University Press, 1997.