磁極結構對永磁同步伺服電機轉矩脈動的影響

于慎波，李 野，鐘雙雙

(沈陽工業大學 機械工程學院，沈陽 100870)

0 前言

隨著我國對稀土能源的有效利用，電機材料及相關加工工藝的完善，永磁電機得到了廣泛的應用。高性能的交流永磁伺服電動機具有功率因數高、效率高、動態響應速度快、轉動慣量小、低速平穩性好等諸多優點，廣泛用于裝備制造業( 機床、機器人等) 、醫療設備、家用電器等場合[1]。數控機床作為現代生產加工的主力軍更是廣泛采用永磁伺服電機。其獨特新穎的結構設計，使電動機的材料利用率提高，體積小，功率高。傳統永磁同步電機磁極采用瓦片式結構，其永磁體結構產生的氣隙磁密波形近似方波而存在。不同轉子結構的氣隙磁場中諧波含量有較大差異，諧波含量越大，電機的不穩定性越差，同時諧波的存在還會產生附加的轉矩脈動，導致電機產生噪聲和振動[2]。轉矩脈動作為衡量永磁電機質量好壞的標準之一，得到了越來越多學者的關注。文獻[3]通過改進的磁化建模方法，解決不同厚度的磁體數學表達式的解析解，實現電磁轉矩的準確計算和轉矩脈動的削弱。文獻[4]基于齒槽轉矩最小化對永磁極進行結構設計，建立了半閉口槽的磁場分布二維解析解。文獻[5]提出了半閉口槽解析子域模型，該模型準確地反映了電樞反應磁場和槽間相互影響，為綜合降低轉矩脈動提供理論支撐。文獻[6]以內置式永磁同步電機為研究對象，提出“M”型新轉子結構，以優化氣隙磁密，減少諧波分量。文獻[7]采用解析法和有限元法相結合的方式，闡述閉口槽降低齒槽轉矩的有效性。文獻[8]分析解釋了拼接式閉口槽的合理性，并對不同拼接方式進行對比分析。本文將以拼接式閉口槽永磁同步電機作為分析對象，提出三段弧磁結構，對比傳統瓦片式磁極，建立不同結構的永磁體有限元模型。通過改變優化磁極外形參數，改變電機氣隙磁場分布規律，進而實現對電機氣隙磁場的優化，使繞組的反電動勢波形盡可能接近理想波形，以此來削弱電機的轉矩脈動。

1 磁極的弧形理論

1.1 基本磁極理論

探究永磁同步電機的轉矩波動，可以從兩方面考慮，第一，考慮定子齒槽對氣隙磁場的影響，即盡可能的降低電機的齒槽轉矩。第二，考慮電機永磁體產生的磁場對氣隙磁場的影響。當忽略電機定子齒槽對氣隙磁場分布的影響時，氣隙磁場的磁密曲線呈矩形分布。將永磁體沿周向展開理想化得到永磁體外表面形函數。圖1為傳統瓦片式磁極結構。

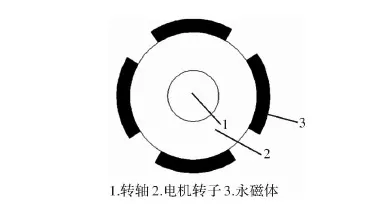
圖1 傳統瓦片式磁極

對應的函數如下[9]：

(1)

其中A(l)為圓弧形狀函數，當形狀函數為等半徑圓弧時，A(l)為定值。將式(1)進行傅里葉級數展開。傅里葉級數展開形式為

(2)

式中，

(3)

(4)

an和bn為傅里葉系數。由于式(1)關于原點對稱，為奇函數，所以其傅里葉級數展開式只含有正弦項。將式(1)做諧波分析，然后進行奇延拓，傅里葉級數展開可得

(5)

(6)

其中k=1,2,3,…,因此式(1)可得

(7)

由分析可得，電機的氣隙磁密不含3的倍數次諧波和偶數次諧波。通過采用永磁體周向相對位置固定的分布方式，能夠削弱氣隙磁密的偶次諧波分量，為后續的理論分析提供支撐。

1.2 三段弧磁極理論

由數學分析表明，當永磁體外表面形狀越逼近正弦，其諧波含量越少，振動浮動和轉矩波動也越小。因此提出一種合理化轉子結構：永磁體外表面將由三段圓弧代替，通過對圓弧的形比修正系數和中心截面系數等重要參數進行修正使永磁體外形更逼近正弦。三段弧磁極結構如圖2所示，其中1為轉軸，2為電機轉子，3為三段弧磁極。相應的函數可簡化為

(8)

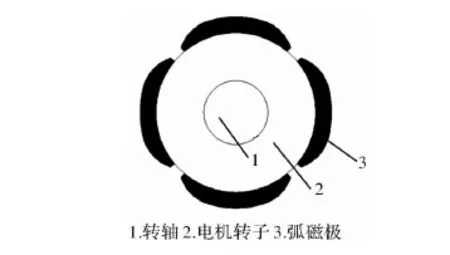
圖2 三段弧式磁極

其中A(l)分別為中間段圓弧形狀函數，B(l)為兩側段圓弧形狀函數。為了獲得良好的性能，將兩側圓弧認為關于中心圓弧對稱分布。由于F(x)為奇函數，故諧波分析奇延拓后可得

B(l)(cosnb1+cosna1-cosnb1-cosna2)]

(9)

對式(9)做進一步分析，假設a1=π-l1，a2=π-l2，b1=l2，b2=l1，且l1=5π/2-l2，A(l)=βB(l)，其中β為形比修正系數，將參數帶入式(9)，則

其中k=1,2,3,…。通過對式(9)的傅里葉級數展開如下

(10)

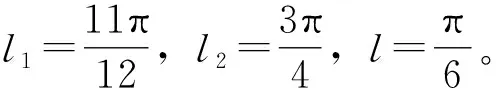
(11)

結合式(11)再將β、l1、l2、l分別代入式(7)和式(10)中，可得

(12)

當且僅當n=12的倍數時，均值不等式兩側相等。在假設條件下，磁極采用三段弧形設計的基波幅值分量要小于傳統瓦片式磁極。但這種條件下卻能有效的減少氣隙磁場中的非零諧波分量，使電流波形、反電動勢波形更接近正弦，因此三段弧磁極的構想是可行的。

2 電機的有限元分析

2.1 電機結構和參數設計

根據理論參數對三段弧式磁極形函數進行結構參數化擬合。通過MATLAB等數據處理軟件對數據點進行曲線擬合，得到三段弧式磁極形狀參數。根據此條件下擬合得到的形狀參數建立有限元仿真模型。擬合得到三段弧參數如表1所示。

表1 三段弧擬合參數

為了降低定子齒槽對氣隙磁場的影響，有限元模型采用表貼式閉口槽永磁同步伺服電機為基礎模型，其定子采用定子沖片拼接而成，考慮到模型的結構和仿真精度，會對其適當簡化。具體模型如圖3所示。

永磁體材料采用釹鐵硼，極對數為4，定子沖片數為12，定子節距為1，每個線圈312匝，電機結構參數如表2所示。

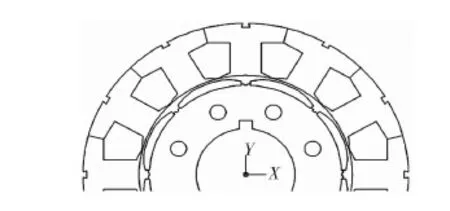
圖3 基礎模型的電機結構

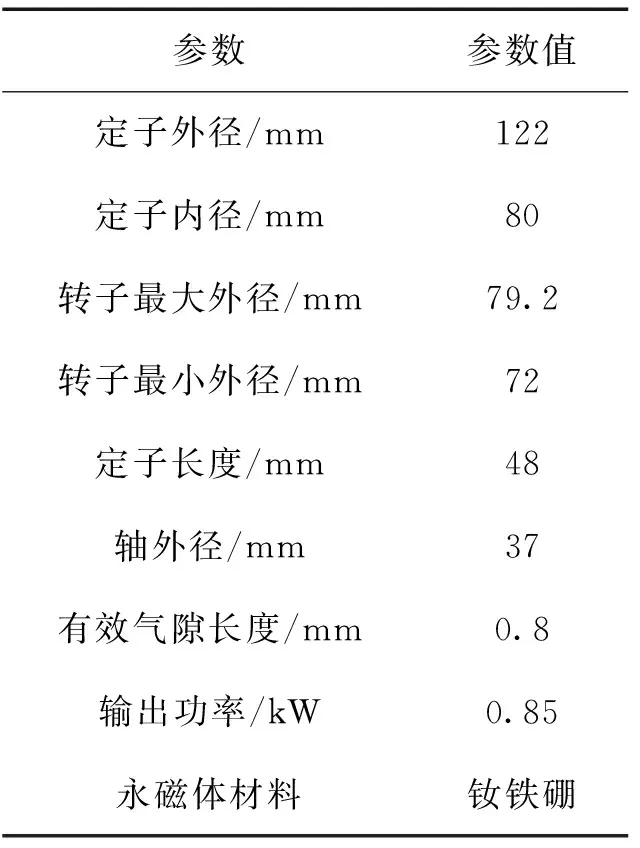
參數參數值定子外徑/mm122定子內徑/mm80轉子最大外徑/mm79.2轉子最小外徑/mm72定子長度/mm48軸外徑/mm37有效氣隙長度/mm0.8輸出功率/kW0.85永磁體材料釹鐵硼

2.2 永磁體截面中心系數

為了最大限度得到弧形最優解，有效控制永磁體外形函數，假設中心弧度角兩側對應的弧度角相等，且兩側弧長半徑均相等。即將永磁體外表面分成三段，中間部分由中心弧度角決定，其圓弧形狀函數為A(l)，其余兩側相互對稱，采用擬合得到的半徑和圓心，其圓弧形狀函數為B(l)，為了體現圓弧形狀函數A(l)，現定義永磁體截面中心系數為:

(13)

式中，角α為電機轉子永磁體的極距；角θ為永磁體中心弧度角。當Kc等于0時磁極為最初的瓦片式結構。

通過修改永磁體截面中心系數，定量研究永磁體不同中心系數下的轉矩脈動和額定轉矩變化趨勢，確定有效的磁極外形結構，降低轉矩脈動及反電動勢中的諧波。

如圖4所示，其中R1為定子內徑，R2為永磁體最大半徑，R3為永磁體與轉子接觸面的半徑。R4為轉子內徑。其中b為永磁體徑向最大厚度。充磁方式采用徑向充磁。運用ansoft仿真出基礎模型的磁場分布如圖5所示。

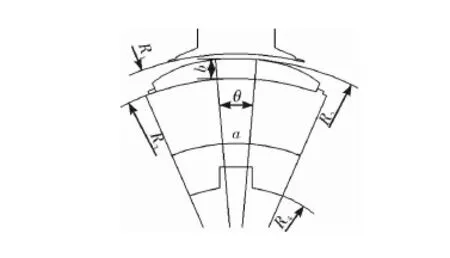
圖4 永磁體截面參數圖

圖5 基礎模型的磁力線分布圖

3 電機仿真分析

應用ansoft對不同中心系數下的氣隙形狀進行有限元分析，如圖6所示。

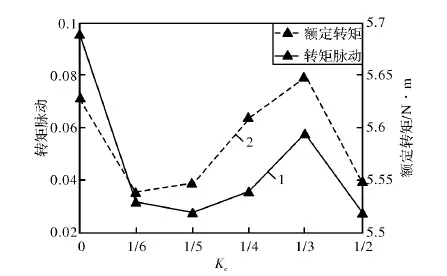
圖6 不同中心系數下的轉矩脈動和額定轉矩

由圖6可知，永磁體表面形狀是影響轉矩脈動的重要因素，因為永磁體表面形狀對氣隙磁導的影響，會嚴重影響氣隙內的磁場分布，從而影響轉矩脈動的變化。圖6中的曲線1為不同中心系數下轉矩脈動的趨勢，曲線2為不同中心系數下的額定轉矩的變化趨勢。綜合圖6中的雙曲線可以確定，三段弧結構能夠有效降低電機的轉矩波動。當Kc等于1/5或Kc等于1/2的時候，轉矩脈動最小同時額定轉矩降低率較低。從經濟角度考慮，當Kc等于1/2的時候，永磁體用量大。因此當Kc等于1/5時，為最優值。

考慮到充磁方式也會影響Kc，因此再采用徑向充磁對現有模型進行仿真。仿真結果如圖7所示。

由圖7可知，本樣機在徑向充磁下的轉矩脈動分布情況與平行充磁的轉矩脈動分布情況類似。通過圖6和圖7中轉矩脈動曲線對比可以，徑向充磁下的轉矩脈動值普遍大于平行充磁下的轉矩脈動值。但當Kc為0和1/3時，兩種情況下的轉矩脈動相近。通過圖6和圖7中的額定轉矩曲線對比可知，徑向充磁與平行充磁對額定轉矩削弱程度相近，徑向充磁對額定轉矩的削弱程度更大一些。因此，對于本樣機而言，采用平行充磁更好。

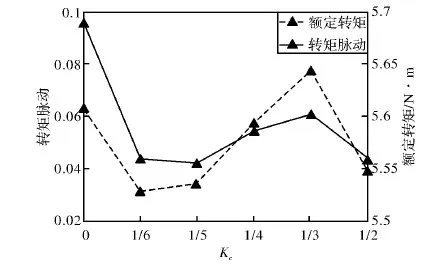
圖7 徑向充磁不同中心系數下的額定轉矩和轉矩脈動

取Kc等于1/5時的電機模型仿真結果得到徑向氣隙磁密如圖8所示。輸出轉矩如圖9所示。同時將三段弧磁極下的單相反電動勢與瓦片式磁極下的單相反電動勢做對比，得出三段弧磁極能夠有效的改善反電動勢波形，減少諧波分量。如圖10、圖11所示。

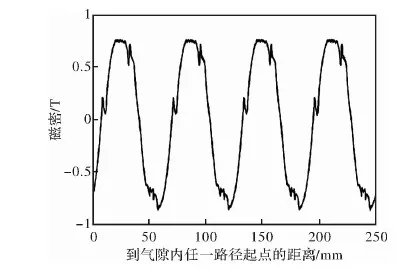
圖8 三段弧磁極徑向磁密

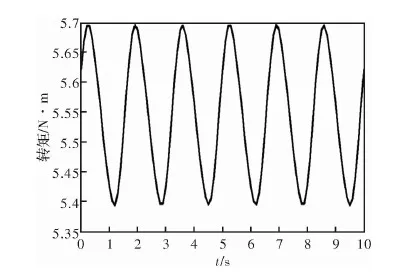
圖9 三段弧磁極輸出轉矩

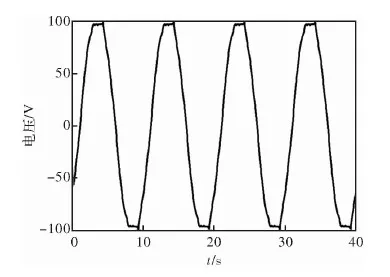
圖10 瓦片式磁極單相反電動勢

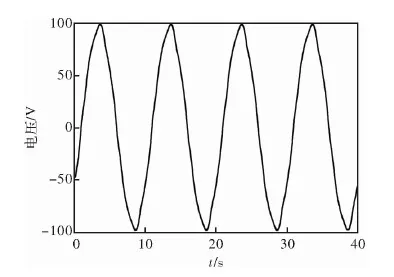
圖11 三段弧磁極單相反電動勢

4 結論

本文主要研究了削弱高精密數控機床用永磁同步伺服電機轉矩脈動的方法，通過對8極12槽拼裝式閉口槽永磁同步伺服電機進行有限元分析發現：三段弧磁極比傳統瓦片式磁極擁有更優良的特性。改善永磁體外表面的形狀能夠影響氣隙分布，進而削弱轉矩脈動。通過改變永磁體截面中心系數，仿真出不同情況下的轉矩脈動和額定轉矩的變化規律。綜合仿真分析結果：采用三段弧式磁極結構，Kc等于1/5并采用平行充磁時為最優參數，此時轉矩脈動為2.73%。研究發現，合理改變永磁體外表面的結構和充磁方式能夠有效的降低轉矩脈動。

[1] 唐任遠，趙清，周挺．稀土永磁電機正進人大發展的新時期[J]．沈陽工業大學學報，2011，33(01)：1-8.

[2] 方程，許海平，薛劭申，等．直驅型多相永磁同步電機定子磁動勢與氣隙磁密特性分析[J]．中國電機工程學報，2013，33(24)：106-113．

[3] S.-M. Jang, H.-I. Park, J.-Y. Choi, K.-J. Ko, and S.-H. Lee.Magnet pole shape design of permanent magnet machine for minimization of torque ripple based on electromagnetic field theory[J].IEEE Trans.Magn.,2011,47(10) : 3586-3589

[4] B. L. Chikouche, K. Boughrara, and R. Ibtiouen.Cogging torque minimization of surface-mounted permanent magnet synchronous machines using hybrid magnet shapes[J].Progress Electromagn. Res. B, 2015,64: 49-61.

[5] T.Lubin, S. Mezani,and A. Rezzoug,2-d exact analytical model for surface-mounted permanent-magnetmotorswith semi-closed slots[J].IEEE Trans. Magn.,2011,45(02) : 479-492.

[6] 張炳義，張霄霆，姜珊珊.電動汽車永磁同步驅動電機優化波形質量方法[J]．沈陽工業大學學報，2017，39(05)：481-485.

[7] 周洲,楊立.降低齒槽轉矩的閉口槽結構永磁無刷電機分析及設計方法[J].微電機，2014,47(05)：6-8.

[8] 袁健,沈建新, 史涔溦等.定子拼裝式永磁同步電機齒槽轉矩研究[J].微電機,2015,48(03)：1-4.

[9] 王海星,李志義,封海潮.表貼式永磁電機階梯形永磁體設計及特性分析[J].合肥工業大學學報:自然科學版,2015(09)：1197-1201.