基于暴露度-恢復力-敏感度的城市適應氣候變化能力評估與特征分析

趙春黎,嚴 巖,陸詠晴,丁 丁,宋 揚,吳 鋼

1 中國科學院生態環境研究中心城市與區域生態國家重點實驗室,北京 100085 2 清華大學工程物理系,公共安全研究院,北京 100084 3 中國科學院大學,北京 100049 4 北京大學,北京 100871 5 住房和城鄉建設部農村污水處理技術北方研究中心,北京 100085

氣候變化是全球可持續發展面臨的巨大挑戰。雖然全球范圍內溫室氣體減排已經進行了大量努力,但氣候變化的趨勢還將在相當長的時間尺度內繼續發展,人類也將進一步面臨一系列氣候變化不利影響,如食品短缺、海平面升高、颶風、干旱等問題,這些問題對發展中國家和地區的影響尤為嚴重。這種情形下,在繼續加大溫室氣體排放控制的同時,需要積極準備應對氣候變化的不利影響,特別是人口與社會經濟活動高度密集的城市,受氣候變化影響的風險和可能的損失更為嚴重,其中發展中國家受氣候變化影響的風險更高。但從目前情況來看,城市應對氣候變化更重視減緩措施,適應氣候變化能力的研究和實踐卻相對滯后,監測、評估技術體系薄弱,適應氣候變化體制、機制不健全,資金投入不足等,氣候變化適應能力成為城市應對氣候變化的短板。

目前,我國城市適應氣候變化的研究和實踐剛處于起步階段。學者Araos等對全球401個大型城市適應氣候變化能力進行了評價,我國入選的城市大部分處于無適應措施或適應措施不足的狀態[1]。近幾年,我國對氣候變化的適應越來越關注和重視,2013年國家發展和改革委員會發布了《國家適應氣候變化戰略》,2016年國家發展改革委和住房城鄉建設部發布聯合發布了《城市適應氣候變化行動方案》,2016年國家發展改革委和住房城鄉建設部啟動了氣候適應型城市建設試點,全國28個城市作為第一批入選城市。這些戰略、方案的出臺和氣候適應型城市試點建設,對我國氣候變化適應,尤其是城市適應氣候變化提出了戰略性、指導性的框架和對策,極大的提升了對氣候變化適應的認識和重視程度,有效的推動了城市的氣候適應能力建設。但總的來說,目前我國城市適應氣候變化工作還處在初始探索的階段,還沒有形成針對氣候變化的區域性特征和具體城市實際的有針對性、系統性、科學性的城市適應氣候變化能力建設對策體系,需要從氣候變化和城市本底特征兩個主要方面進行更為深入、系統的分析和研究。

本文以我國286個地級市為研究尺度和對象,從暴露度、敏感度和恢復力的角度研究城市適應氣候變化能力的評估方法,進而分析我國城市適應氣候變化的特征和關鍵因素,為城市適應氣候變化能力評估提供方法支持,為科學制定城市適應對策提供科學參考。

1 方法與數據

1.1 評價框架與指標體系

本文構建了基于IPCC的適應能力評價的評估算框架與指標體系。IPCC的適應能力評價模型,是在脆弱性評價的基礎上進行的。第三次評估報告中的脆弱性定義被廣泛運用,即系統易受氣候變化造成的不良影響或者無法應對其不良影響的程度。氣候變化風險包括氣候變化的危害,脆弱性和暴露度,社會經濟路徑、適應和減緩路徑以及治理等[2]。本文將氣候變化適應總結為“暴露度”、“敏感度”和“恢復力”的函數[3],并從這3個方面,梳理和總結出我國城市適應氣候變化能力指標體系(表1)。

基于以上評估框架,本研究構建了城市適應氣候變化能力評估的指標體系,其中暴露度是城市所面臨各類的氣候變化風險,敏感度是城市受氣候變化影響的脆弱程度,恢復力是城市在應對氣候變化中減小氣候影響并快速恢復到原來狀態的能力。

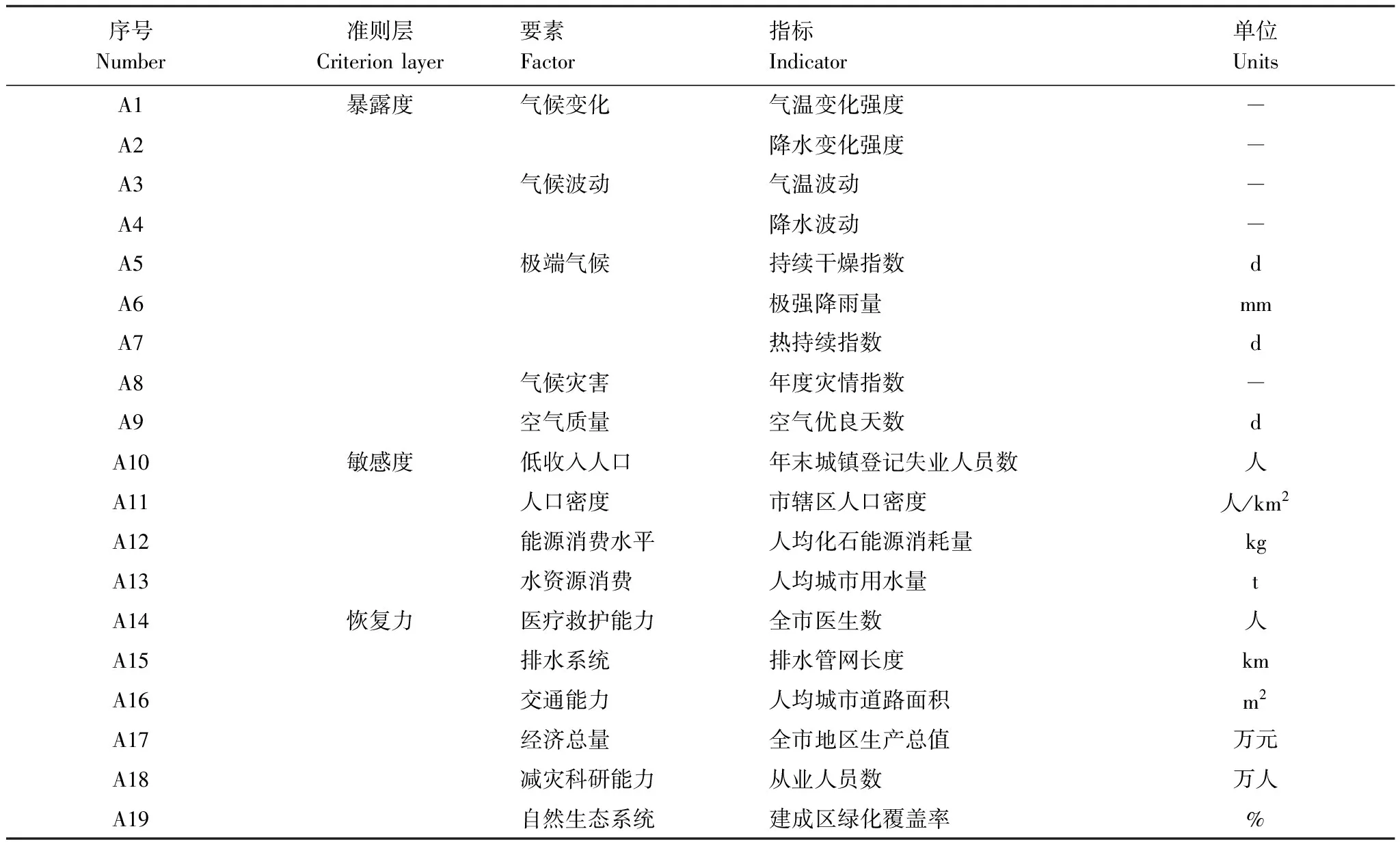
表1 城市適應氣候變化評價指標體系

對以上指標,首先進行歸一化處理,并采用熵值法對指標賦予權重。

成本型指標的歸一化方法如下式,

(1)

效益型指標為

(2)

式中,prk表示經過標準化處理后的第k個城市第r個評價指標的值,drmax和drmin分別表示評價矩陣中各城市的評價指標r的最大值和最小值。歸一化后,原來的成本型指標被轉化為正向指標,所有指標值越大,代表的城市適應能力也越高;即,對暴露度和敏感度這類成本型指標來說,值越小所代表的暴露度或敏感度越高;對恢復力這類效益型指標來說,值越小則恢復力越低。

經過歸一化處理的指標,采用熵值法對指標進行權重賦值。并對指標進行等級劃分,“低”、“較低”、“中”、“較高”和“高”分別是各項指標適應氣候變化能力的5個層次,指標等級主要采用百分位法并參考其自然斷點進行手動劃分。指標等級及其權重值見表2。

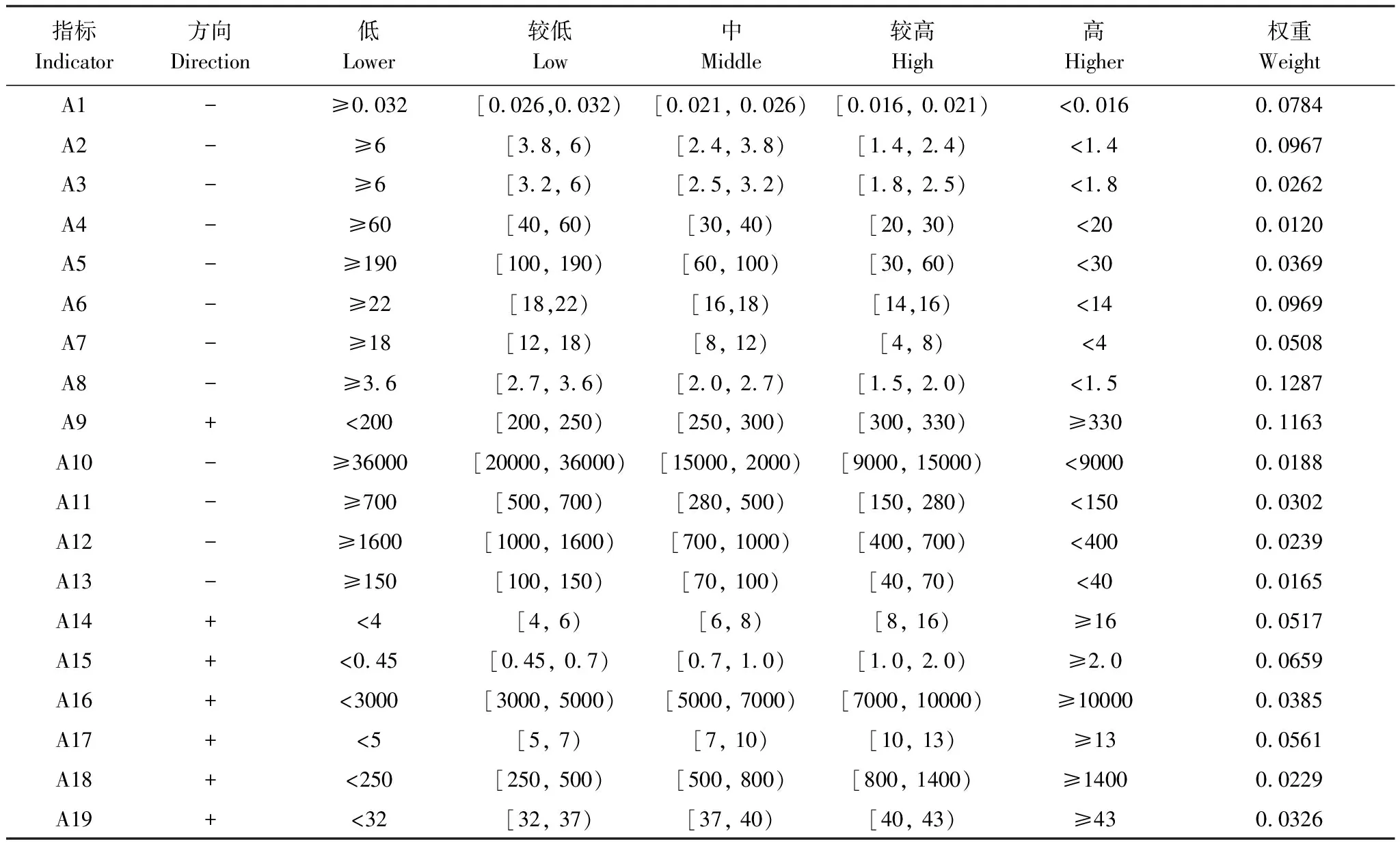
表2 適應氣候變化能力指標等級劃分與權重

表中,“+”和“-”分別代表效益型與成本型指標

1.2 集對分析評價方法

本文采用集對分析(set pair analysis, SPA)方法評價城市適應氣候變化能力。該方法是趙克勤在1989年提出的一種新的系統分析方法。SPA通過聯系數的運算研究來分析含有不確定性的問題,被視為一種新的不確定性系統數學理論[4- 7]，是評價非傳統安全非常有效的新方法。

SPA的核心是把確定、不確定視為一個系統,從同、異、反3個方面研究事物的確定性與不確定性,分析研究事物之間的聯系與轉化[8]。具體來看,根據研究問題φ所需,將集對H的N項特性進行分析,其中有S項為集對H兩集合所共有,有P項相對立的特性,其余F=N-S-P項特性既不對立也不共有,則有如下定義：

S/N為集對H在問題φ下的同一度;F/N為差異度;P/N為對立度,表示為：

(3)

式中，i為差異度系數,j為對立度系數。也可以簡化為：

μ=a+bi+cj其中a+b+c=1

(4)

進一步簡化得為：

μ′=a+cj

(5)

或μ′=a+bi

(6)

μ′=bi+cj

(7)

式中，μ是集對H的聯系度,根據以上公式過程可以看出,μ是兩個集合或者一個系統在所研究問題下得到的同一度、對立度和差異度的代數和。

同樣,可以將聯系度表達式進一步展開,得到多元聯系度。例如,展開差異度b,即：

μ=a+b1i1+b2i2+…+bnin+cj

(8)

同樣,展開對立度c,即：

μ=a+c1j1+c2j2+…+cnjn+bi

(9)

當n=3代入上式時,即得到：

μ=a+b1i1+b2i2+b3i3+cj

(10)

同理,n元聯系度的概念就可以得到。其中,b1,b2,b3也可以被稱為差異度分量,即差異度有不同級別,如輕度差異度,中度差異度,重度差異度等,i1,i2,i3也被稱為差異不確定分量系數[9]。

本文將我國城市適應氣候變化能力評價指標劃分為5個等級,城市適應能力的確定采用SPA等級和貼近度分析這兩種差異度系數確定方法。

SPA等級是指,在本文采用3元聯系度的評價中,公式(8)中的參數可為理解為：a為xl隸屬于1級標準的可能程度,b1為xl隸屬于2級標準的可能程度,b2為xl隸屬于3級標準的可能程度,b3為xl隸屬于4級標準的可能程度,c是xl隸屬于5級標準的可能程度[9]。

貼近度及其排序方法的具體計算公式如下[10- 11]：

(11)

式中,rk為貼近度值,rk值越大,則城市樣本k越接近最優方案,城市適應氣候變化的能力越強。

各樣本聯系數的確定,可基于下式計算得到[9,12]。對于成本型指標(值越小越優),樣本值xl與指標1級評價標準的聯系度為μl：

(12)

式中,s1≤s2≤…≤sK-1≤sK,分別為等級1,2,…,K-1,K等級的分界值。

對于效益型指標(值越大越優),某樣本值xl與指標1級評價標準的聯系度為μl為：

(13)

式中,s1≥s2≥…≥sK-1≥sK。

1.3 數據

本文數據來源為,氣象數據下載自中國氣象數據網(http://data.cma.cn/site/index.html),使用其地面氣象資料的“中國地面氣候標準值數據集”產品;氣候災害數據來源于《2014年自然災害圖集》;其他數據主要來源于城市統計年鑒、城市建設統計年鑒、社會經濟發展公報等。本文的評價是基于2010年各項數據進行的,其中氣候數據是基于1951—2010年60年間的變化值;受數據限制,氣候災害和空氣質量數據,選取2014年的值替代,其他值均為2010年各類年鑒數據。

2 結果與分析

2.1 SPA評價等級

基于以上數據和權重值,采用SPA評估的中國城市適應氣候變化能力等級,這五個等級適應能力各自對應著的城市數量為：高(105),較高(51),中(6),較低(7),低(117)。圖1展現了其空間分布情況。

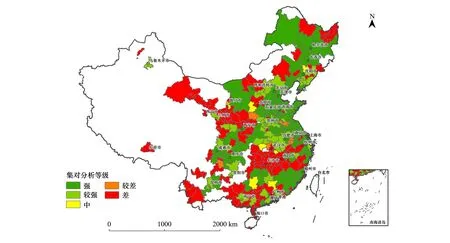
圖1 集對分析等級空間分布Fig.1 Set pair analysis (SPA) result of urban adaptation capacity grades

可以看出,適應能力高的城市分布較為分散,大部分處于我國東部地區。適應能力低的城市主要集中在3個區域,西部的甘肅、陜西和河南地區;中部的湖南、江西、浙江等地;以及南部的廣西、云南等地區。

城市適應氣變化能力等級分布在“高”“低”這兩個等級的城市占到了絕大多數,這可能受到了指標等級劃分的影響。

2.2 貼近度分析

依據rk的大小進行城市適應氣候變化能力的排序,其適應能力評價結果如圖2所示。

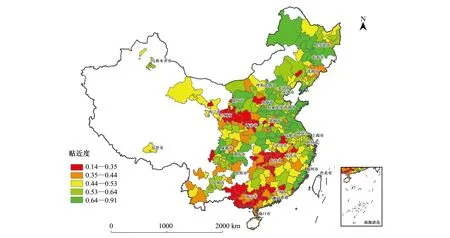
圖2 貼近度空間分布Fig.2 Close degree result of urban adaptation capacity

從圖中看出,東部地區整體狀況較好;適應能力較低的區域集中在3個區域,分別為：西北的蘭州-西安等城市,涵蓋陜西、甘肅、河南和寧夏四省/自治區;西南的云南、廣西等城市;以及華中的湖南、湖北、江西等城市。

可以看出,貼近度分析的結果與城市的適應能力的排序基本一致,但貼近度系數更好的拉開城市適應能力的差距。

2.3 關鍵限制要素分析

這一部分主要討論城市適應能力限制要素及其空間分布,主要從暴露度、敏感度和恢復力3個方面進行。

1)暴露度分析

圖3中標紅色的地區為暴露度高的城市聚集區域。可以看出,氣候變化風險較高的區域主要在中部,包括湖南、湖北和江西的部分城市。高氣候暴露地區周邊的城市所面對的氣候風險也較高。高的氣候暴露風險,主要是受到年度災情指數(權重為0.1287),持續干燥指數(權重為0.0369),極強降雨量(權重為0.0969),降雨變化強度(權重為0.0967)等因素的影響,其中以年度災情指數的指標權重最高。

圖3 適應氣候變化暴露度空間分布Fig.3 Spatial distribution of exposure element

2)敏感度分析

從圖4可以看出,敏感度分布與胡煥庸線分布有較高的一致性。西北地區人口密度低,對氣候變化的敏感性也較低;東南地區的經濟發展水平較高,聚集了全國90%以上的人口[13- 14],也面臨著比較高的敏感度。整體上,敏感度的格局與胡煥庸線的分布保持較高的一致性,胡煥庸線東南地區整體呈現適應氣候變化更敏感的態勢。

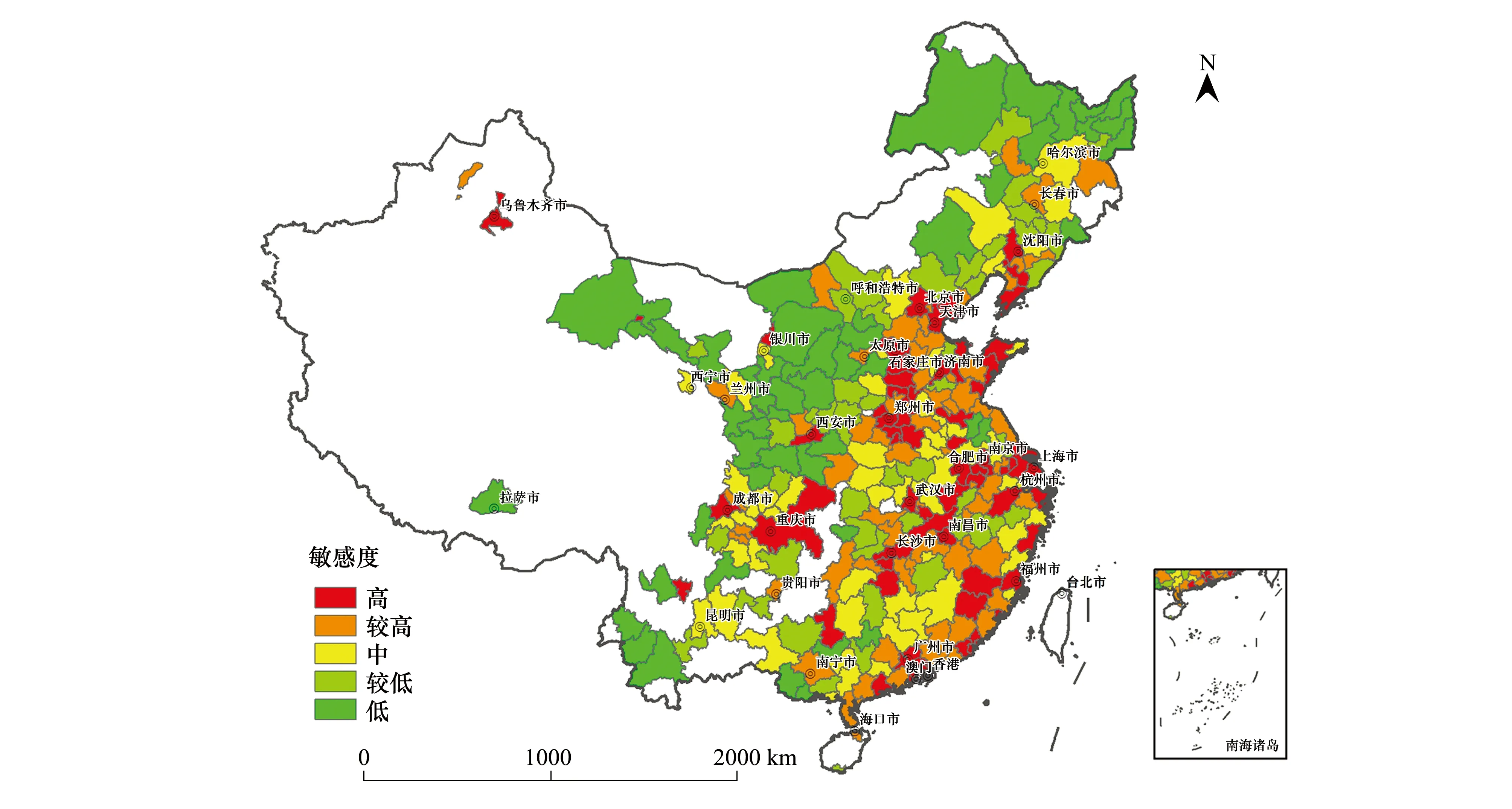
圖4 適應氣候變化的敏感性空間分布Fig.4 Spatial distribution of sensitivity element

3)恢復力分析

恢復力表現為由東部向西部逐漸過渡的空間分布,東部一線的城市恢復力最高,向西一線城市恢復力有所下降,西部地區城市的恢復力最低(圖5)。恢復力指標受到地區經濟發展水平的影響比較大,經濟基礎好的地區,適應氣候變化基礎設施、人員配備較為完備,并且影響發生時能夠迅速調集人員和資金進行恢復和搶救工作。

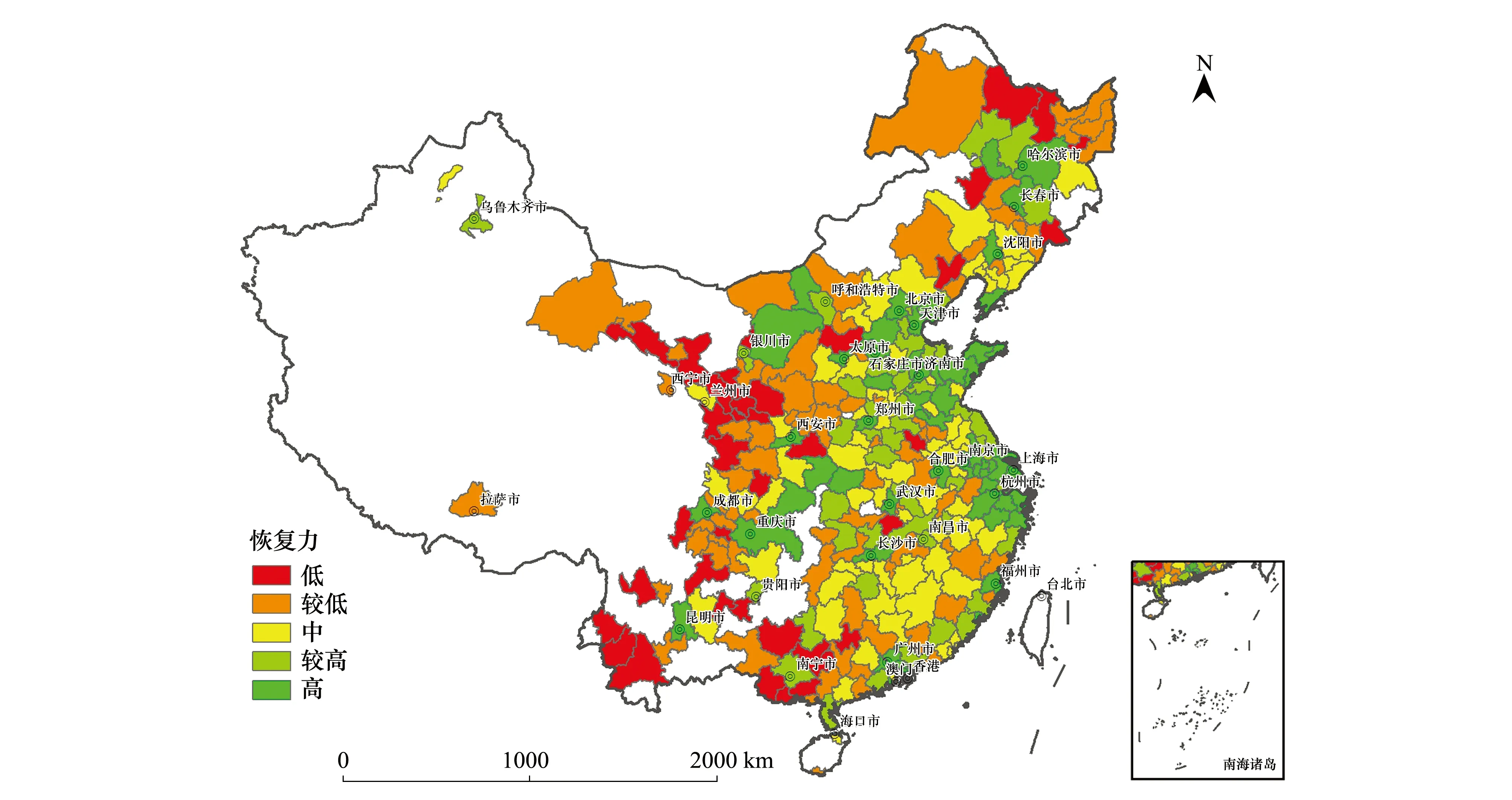
圖5 適應氣候變化的恢復力空間分布Fig.5 Spatial distribution of resilience element

3 討論

圖6 暴露度-敏感度-恢復力等高線圖Fig.6 Contour chart of exposure-sensitivity-resilience

進一步分析各項因素的作用區域,使用SigmaPlot 12.5 對其暴露度-敏感度-恢復力指標做等高線圖(圖6),可以看出,城市適應氣候變化能力的各項限制要素主要表現為,適應能力高主要為暴露度-恢復力-敏感度的(低-高-低)的組合條件;適應能力低則分別為暴露度-恢復力-敏感度(高-高-高)、(低-低-低)和(高-低-低)3種組合。具體到某個城市時,還需要結合城市實際情況等進行具體分析,例如,李彤玥等對蘭州市城市空間脆弱性的研究等[15]。

(1) 暴露度-恢復力-敏感度(高-高-高)類型,主要聚集在圖6右下角的藍色區域,其中除了恢復力較高外,高暴露度和高敏感度都會拉低城市適應氣候變化能力水平。這類城市對應我國中部地區的兩湖和江西等的城市,它們面臨著較高的氣候變化和災害風險,應對氣候變化的敏感性較高,同時恢復能力高。

(2) 暴露度-恢復力-敏感度(低-低-低)的城市類型對應圖中深黃色區域。主要是甘肅、陜西、寧夏等地區的主要城市,表現為氣候變化波動和極端氣候的風險較小,地處西北人口密度低應對氣候變化的敏感性低,當氣候波動、變化或極端氣候帶來影響時,城市的恢復能力也較低。

(3) 暴露度-恢復力-敏感度 (高-低-低)類型城市對應圖中左下角區域,主要為廣西、云南等地的城市,表現為改區域的氣候風險較高,但是敏感性較低,同時遭遇氣候變化影響后的恢復能力也較低。

(4) 暴露度-恢復力-敏感度(低-高-低)類型城市對應圖中右上角區域,這類城市主要分布在我國的東北地區,也是適應氣候變化能力較高的一類城市,首先其暴露程度較低,應對氣候變化的敏感性也低,恢復力高。

4 結論與建議

通過本文的研究主要得出以下結論：東部城市適應氣候變化能力相對較好,西部相對較差;適應能力較低的城市主要集中在3個區域,西北的蘭州-西安等城市,西南的廣西的部分城市,華中地區湖南-江西等部分城市等。適應能力較低的城市類群,主要面對的問題分別是,華中城市面臨著較高的氣候變化和災害風險,應對氣候變化的敏感性較高,恢復能力強,主要限制因素是高的暴露度和敏感度;甘肅-陜西等西北城市,其所面對的氣候暴露度較小,敏感性低,但是關鍵是其應對氣候變化的恢復力也較弱;位于西南地區的廣西-云南地區的低適應能力區,雖然敏感性較低,但是氣候風險高,同時恢復力也較低。針對以上問題,不同區域提高城市適應氣候變化能力的側重點也各有不同,對于華中、西南城市主要工作是提高氣候風險的防御能力,西北的甘肅-陜西等城市,則需要提高應對氣候變化的恢復能力,建立良好的災后恢復與應急系統。

參考文獻(References):

[1] Araos M, Berrang-Ford L, Ford J D, Austin S E, Biesbroek R, Lesnikowski A. Climate change adaptation planning in large cities: a systematic global assessment. Environmental Science & Policy, 2016, 66: 375- 382.

[2] IPCC. Climate Change 2014: Impacts, Adaptation and Vulnerability. Cambridge: Cambridge University Press, 2014.

[3] 姜彤, 李修倉, 巢清塵, 袁佳雙, 林而達. 《氣候變化2014: 影響、適應和脆弱性》的主要結論和新認知. 氣候變化研究進展, 2014, 10(3): 157- 166.

[4] 趙克勤. 集對分析中的不確定性理論. 大自然探索, 1995, 14(54): 87- 88.

[5] 趙克勤. 集對分析(SPA)中的聯系數與不確定量. 大自然探索, 1997, 16(60): 91- 91.

[6] 趙克勤. 集對分析及其初步應用. 杭州: 浙江科學技術出版社, 2000.

[7] 趙克勤. 二元聯系數A+Bi的理論基礎與基本算法及在人工智能中的應用. 智能系統學報, 2008, 3(6): 476- 486.

[8] 張斌. 多目標系統決策的模糊集對分析方法. 系統工程理論與實踐, 1997, (12): 108- 114.

[9] 王文圣, 金菊良, 丁晶, 李躍清. 水資源系統評價新方法——集對評價法. 中國科學 E輯: 技術科學, 2009, 39(9): 1529- 1534.

[10] 張斌. 集對分析與多屬性決策. 農業系統科學與綜合研究, 2004, 20(2): 123- 125.

[11] 姚治華, 王紅旗, 郝旭光. 基于集對分析的地質環境承載力研究——以大慶市為例. 環境科學與技術, 2010, 33(10): 183- 189.

[12] 劉秀梅, 趙克勤. 基于SPA的D-U空間的區間數多屬性決策模型及應用. 模糊系統與數學, 2009, 23(2): 167- 174.

[13] 陳明星, 李揚, 龔穎華, 陸大道, 張華. 胡煥庸線兩側的人口分布與城鎮化格局趨勢——嘗試回答李克強總理之問. 地理學報, 2016, 71(2): 179- 193.

[14] 吳瑞君, 朱寶樹. 中國人口的非均衡分布與“胡煥庸線”的穩定性. 中國人口科學, 2016, (1): 14- 24, 126- 126.

[15] 李彤玥. 基于“暴露—敏感—適應”的城市脆弱性空間研究——以蘭州市為例. 經濟地理, 2017, 37(3): 86- 95.