混煉機橫截面PP熔體液滴分散過程的數值模擬研究

郝玉婷，陳 濤，馬玉錄，謝林生

(綠色高效過程裝備與節能教育部工程研究中心，華東理工大學動力工程學院，上海 200237)

0 前言

采用共混改性法獲得各組分性能互補的多相聚合物，已成為制備新材料的重要途徑之一。共混物中分散相的形貌結構和尺寸大小是決定共混物性能的重要因素之一。液滴代表了單個分散相，研究單個液滴的分散過程對了解分散相織態結構發展演變過程和機理具有指導意義。當2種聚合物共混時，分散相會在流場作用下發生變形、破碎和二次團聚過程。液滴在流場中發生的變形程度用變形度D來表示，可通過式(1)計算：

(1)

式中L——液滴的長度，m

R——液滴的特征半徑，m

毛細管數Ca用來表征液滴在剪切流場下的受力情況。在流場中，液滴同時受到界面張力和剪切應力的作用。兩種力的作用效果相反，界面張力使液滴收縮，變形度減小，而剪切應力使液滴發生變形，變形度增大，兩者的比值稱為毛細管數[1]，可通過式(2)計算：

(2)

式中ηm——連續相黏度，Pa·s

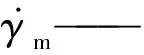
σ——兩相間界面張力，N/m

當液滴在流場中受到的毛細管數小于臨界毛細管數時，液滴會發生微小變形，最終達到穩定形狀，變形度與毛細管數成正比[2]；當液滴受到的毛細管數等于臨界毛細管數時，液滴會發生破碎；當液滴受到的毛細管數大于臨界毛細管數時，液滴會發生持續變形，使得液滴半徑逐漸減小，最終液滴受到的毛細管數等于臨界毛細管數，液滴發生破碎。其中臨界毛細管數與流場特性以及兩相黏度比有關。破碎形成的小尺寸液滴在流場中碰撞會發生二次團聚。最終分散相尺寸是由液滴破碎與二次團聚過程共同決定的[3]。目前國內外學者對液滴變形、破碎行為的研究只限于簡單流場[4]，而混煉腔內隨著2個轉子相位角的交替變化，流場呈現出復雜、動態變化的特點[5-8]。本文通過對液滴在轉子橫截面上的分散過程的模擬，將更直觀地了解混煉設備中分散相的形貌演變過程。

1 模型建立

1.1 VOF模型及控制方程

VOF模型是一種基于歐拉法追蹤不能相互滲透的多相流動自由界面的模擬方法。該模型是在單相流的基礎上對每一相引入一個體積分數標量αq。該αq是第q相流體在單元格中占據的體積分數。當αq=0時，說明該單元格內不存在第q相流體；當αq=1時，說明該單元格內全部被第q相流體占據；當0<αq<1時，說明該單元格中存在不同相的相界面。單元格內各相體積分數之和為1。體積分數控制方程如式(3)所示：

(3)

式中v——速度矢量，m/s

控制方程中各物性參數φ是由控制體中各相各自的物性參數φq以及體積分數αq決定的，可通過式(4)計算：

φ=∑αqφq

(4)

本文研究的是等溫不可壓縮流體。控制方程包括連續性方程、動量方程以及黏彈性本構方程，分別如式(5)～(8)所示：

(5)

(6)

(7)

(8)

式中ui——i方向速度，m/s

xi——x,y,z3個分量坐標，m

ρ——密度，kg/m3

p——壓力，Pa

μ——黏度，Pa·s

λ——松弛時間，s

Cij——柔性高分子聚合物的變形張量，為對稱張量

δij——克羅內克符號，i=j時，其值為1，i≠j時，其值為0

黏彈性高分子聚合物變形張量Cij的輸運方程采用Oldroyd-B模型如式(9)所示：

(9)

在Fluent中，采用Coupled算法處理壓力與速度的耦合，壓力方程采用PRESTO格式進行離散，動量方程與用戶自定義標量方程采用QUICK格式進行離散。

1.2 物理模型及物性參數

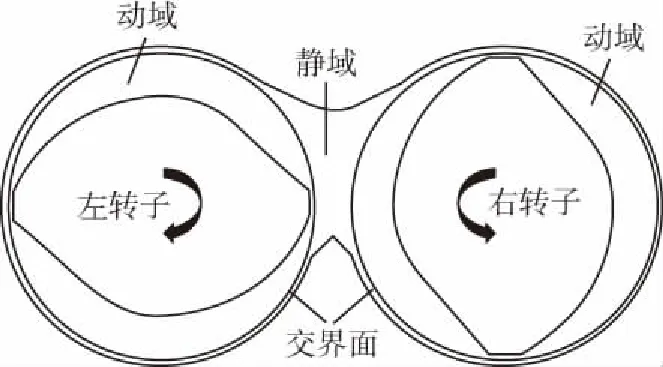
圖1 滑移網格計算域劃分示意圖Fig.1 Sliding grid computing domain division diagram

選取混煉機橫截面作為計算對象，考慮到多相流界面追蹤VOF模型的復雜性，這里采用等溫二維模型進行模擬計算。兩轉子中心距為22.5 mm，左右2個機筒半徑均為10.5 mm。機筒速度為零，兩轉子以3 rad/s的速度異向旋轉，轉子間相位角為90 (°)。本文使用Gambit建立了轉子二維構型，并在ICEM CFD中采用結構網格進行網格劃分。2個轉子附近動網格設置為滑移網格(圖1)。進行網格無關性驗證后，網格數量確定為36 691。

混煉腔中充滿了聚合物熔體線形低密度聚乙烯(PE-LLD)，分散相聚丙烯 (PP)液滴的直徑為2 mm。兩相間界面張力設置為2 mN/m[9]。使用馬爾文平板流變儀測量得到的PE-LLD與PP 2種材料的物性參數如表1所示。

表1 材料的物性參數Tab.1 Characteristic parameter of PE-LLD and PP

1.3 基本假設

數值模擬基本假設如下：

(1)假設流場為穩定狀態的等溫流場，流動為層流；

(2)假設流體為不可壓縮流體，流道完全充滿；

(3)假設壁面無滑移；

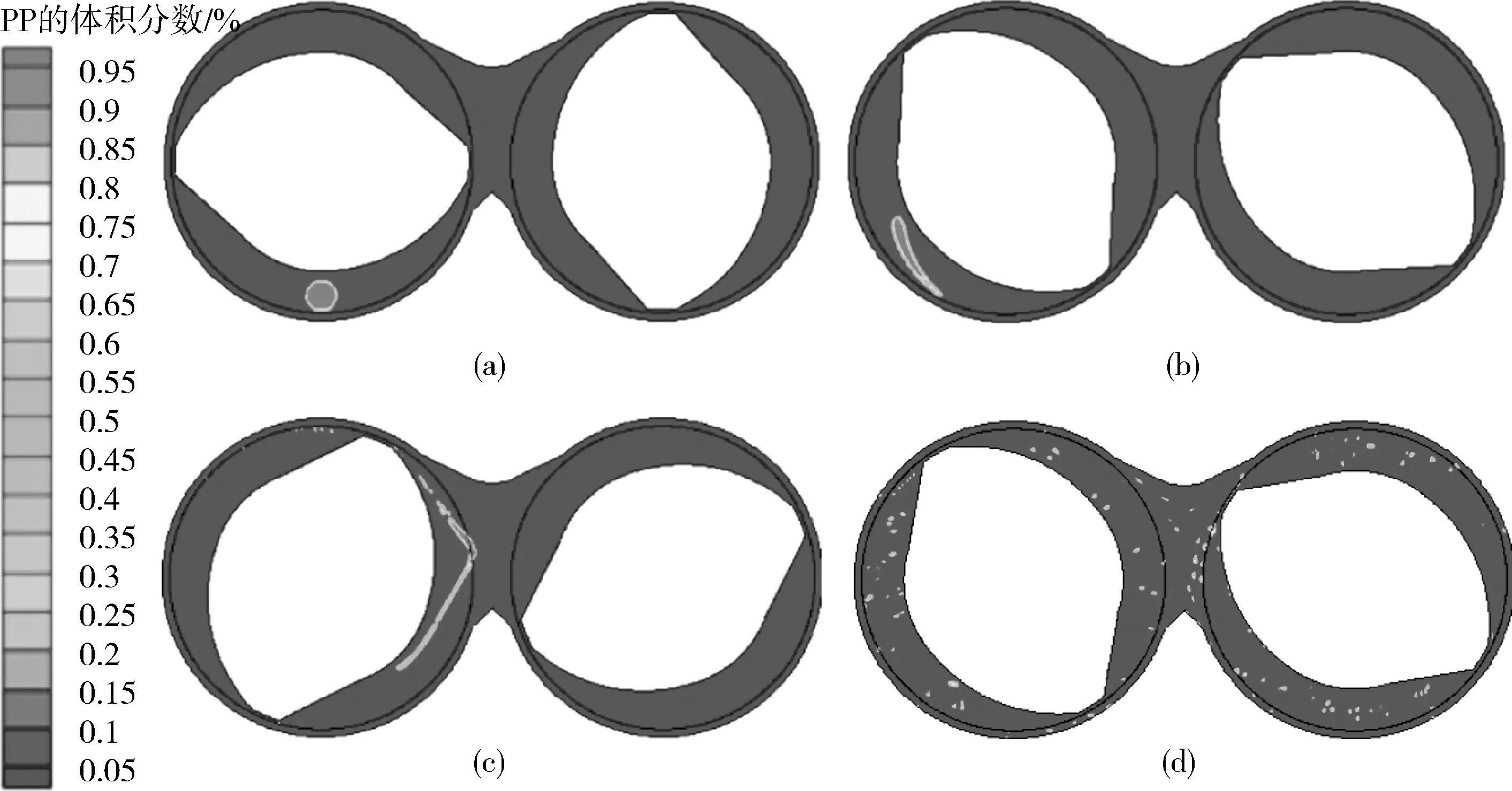
t/s：(a)0 (b)0.3 (c)1.7 (d)15圖2 PP液滴的分散過程Fig.2 Dispersion process of PP droplet

(4)忽略重力、慣性力等體積力的影響；

(5)假設流體黏度為常量，不隨剪切速率變化。

2 結果與討論

2.1 混煉機橫截面PP液滴分散過程的動態分析

本文模擬的是2種材料的共混過程，兩相間存在自由界面。另外由于分散相的變形、破碎與二次團聚，共混是一個不斷發生變化的動態過程，因此要對模擬結果進行瞬態分析。

圖2為不同時刻PP的體積分數云圖。由圖2可知，PP液滴在PE-LLD基體中進行了動態分散。在初始時刻，PP液滴是圓球狀[圖2(a)]。當經過0.3 s時，PP液滴在剪切場中變形為錐狀[圖2(b)]。當經過1.7 s時，PP液滴變形度繼續增大為絲狀[圖2(c)]。液滴變形的同時發生破碎，尺寸變小。最終PP液滴經過15 s分散為細小液滴[圖2(d)]，并在相互作用窗交叉流動作用下[10]，均勻地分布在左右2個混煉腔中。

由圖2(b)可見，PP液滴發生了不均勻變形，其中尾部更細長，變形度大于頭部。圖3為t=0.3 s時流場的剪切速率分布云圖，其中為了方便比較液滴所處位置的剪切速率大小，將液滴位置也顯示在圖中。由圖3可以看出，在轉子橫截面上，剪切速率是繞轉子成同心圓分布的，在壁面處剪切速率較大，轉子根部剪切速率較小，其中螺棱頂部剪切速率最大。由于液滴尾部靠近壁面，頭部靠近轉子根部，尾部受到的剪切速率更大，因此當t=0.3 s時，液滴為錐狀，尾部變形度更大。在接下來的分散過程中，隨著液滴尾部半徑越來越小，液滴尾部毛細管數會先達到臨界毛細管數而先發生破碎。由液滴分散的動態過程可以看出，液滴受到了明顯的剪切、拉伸、折疊，在混煉相互作用窗還進行了充分的物料交換，這對分散相的分散與分布具有重要意義。

圖3 t=0.3 s時流場的剪切速率分布云圖Fig.3 Contour of shear rate at t=0.3 s

2.2 PP液滴拉伸行為分析

圖4為PP液滴不同時刻的體積分數云圖。由圖4可以看出，t=1.7 s時液滴形狀相較于1.5 s時，下半段明顯拉伸變長，說明液滴在混煉相互作用窗發生了大的拉伸變形。

t/s：(a)1.5 (b)1.7圖4 PP液滴的拉伸過程Fig.4 Stretch process of PP droplet

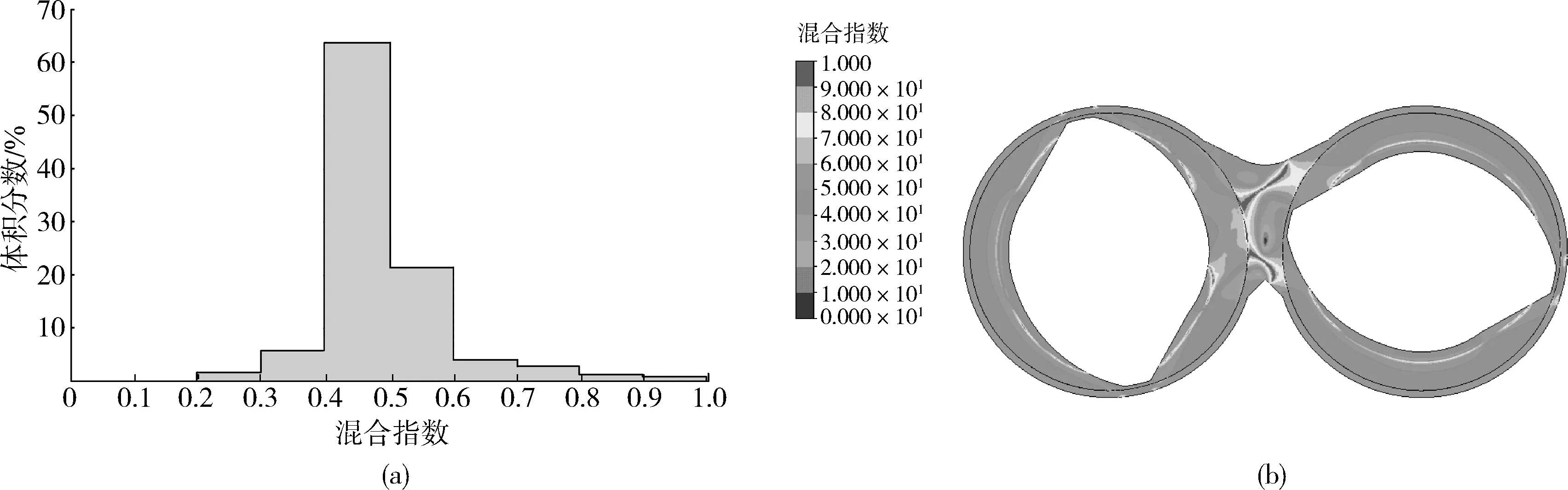
(a)混合指數體積分數分布直方圖 (b)混合指數分布云圖圖6 t=1.5 s時混煉腔內混合指數分布Fig.6 Mixing index distribution at t=1.5 s

拉伸流場比剪切流場對液滴的分散更有效[11]。在相互作用窗，隨著轉子的轉動，物料被不斷的拉伸、擠壓，對分散非常有利。當液滴在C形混煉腔時，速度梯度方向與液滴流動方向相垂直，因此在C形混煉腔液滴主要承受剪切力。而在混煉相互作用窗，流場的瞬時性與物料流動的無序性，導致此處流場具有很強的拉伸作用。圖5為拉伸過程中1.7 s時的速度分布云圖，黑色陰影為液滴輪廓。從圖5可以看出，此時液滴下半段所在位置處的速度梯度與液滴流動方向相同，液滴受到強烈的拉伸作用，因此發生了大的拉伸變形。

圖5 1.7 s時流場的速度分布云圖Fig.5 Contour of velocity at t=1.7 s

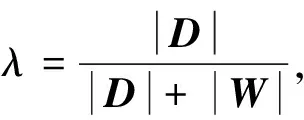
2.3 PP液滴折疊行為分析

圖7為PP液滴在混煉相互作用窗形狀演變過程的體積分數云圖。該模擬初始時刻液滴位置如圖7(a)所示。對比圖7(b)以及圖7(c)，可以看出液滴在混煉相互作用窗發生了折疊，這說明相互作用窗存在強烈的混沌混合。

t/s：(a)0 (b)0.5 (c)0.7圖7 PP液滴的折疊過程Fig.7 Folding process of PP droplet

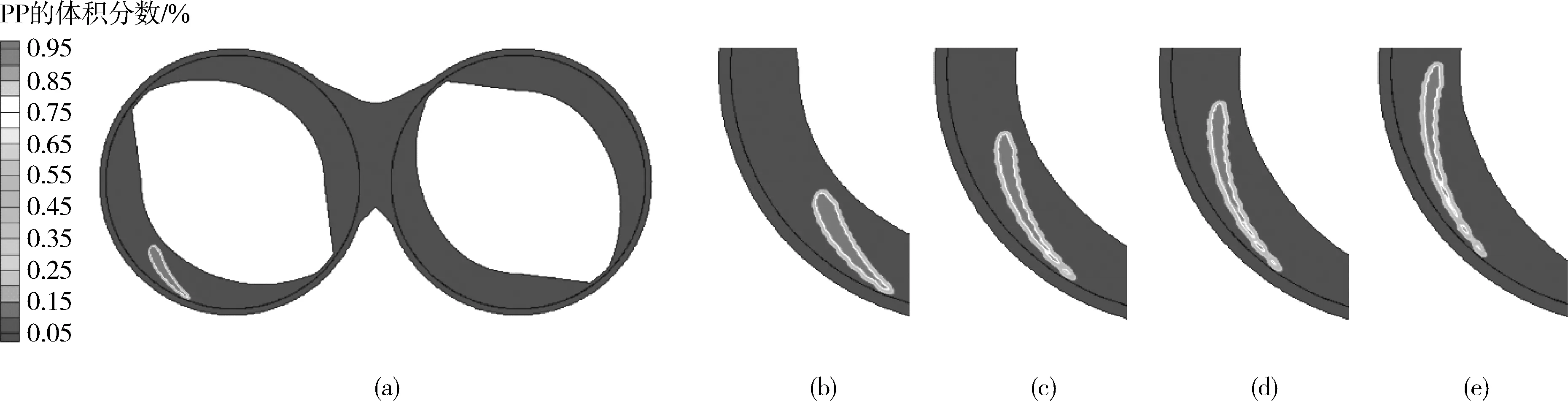
(a)整體圖 (b)t=0.24 s (c)t=0.34 s (d)t=0.39 s (e)t=0.44 s圖9 PP液滴在C形區的破碎過程Fig.9 Breakup process of PP droplet at champer half

由于2個轉子存在90 °相位角，左右轉子螺棱交替經過混煉相互作用窗，所以相互作用窗的形狀以及流場一直在動態變化。而C形混煉區存在從推進面到螺棱背面的壓力梯度，因此相互作用窗兩側總是一個轉子高壓區和另一個轉子低壓區同時存在，在壓差的作用下，物料會出現橫向流動，像是開煉機中“打三角包”。 圖8為t=0.5 s時流場的速度矢量圖，可以看出，在混煉相互作用窗存在S Smale渦旋，使得物料在此處發生交叉、返混流動。當螺棱頂部經過相互作用窗時，相對于螺棱頂部均在左右混煉室時，物料交叉、返混流動更強烈。

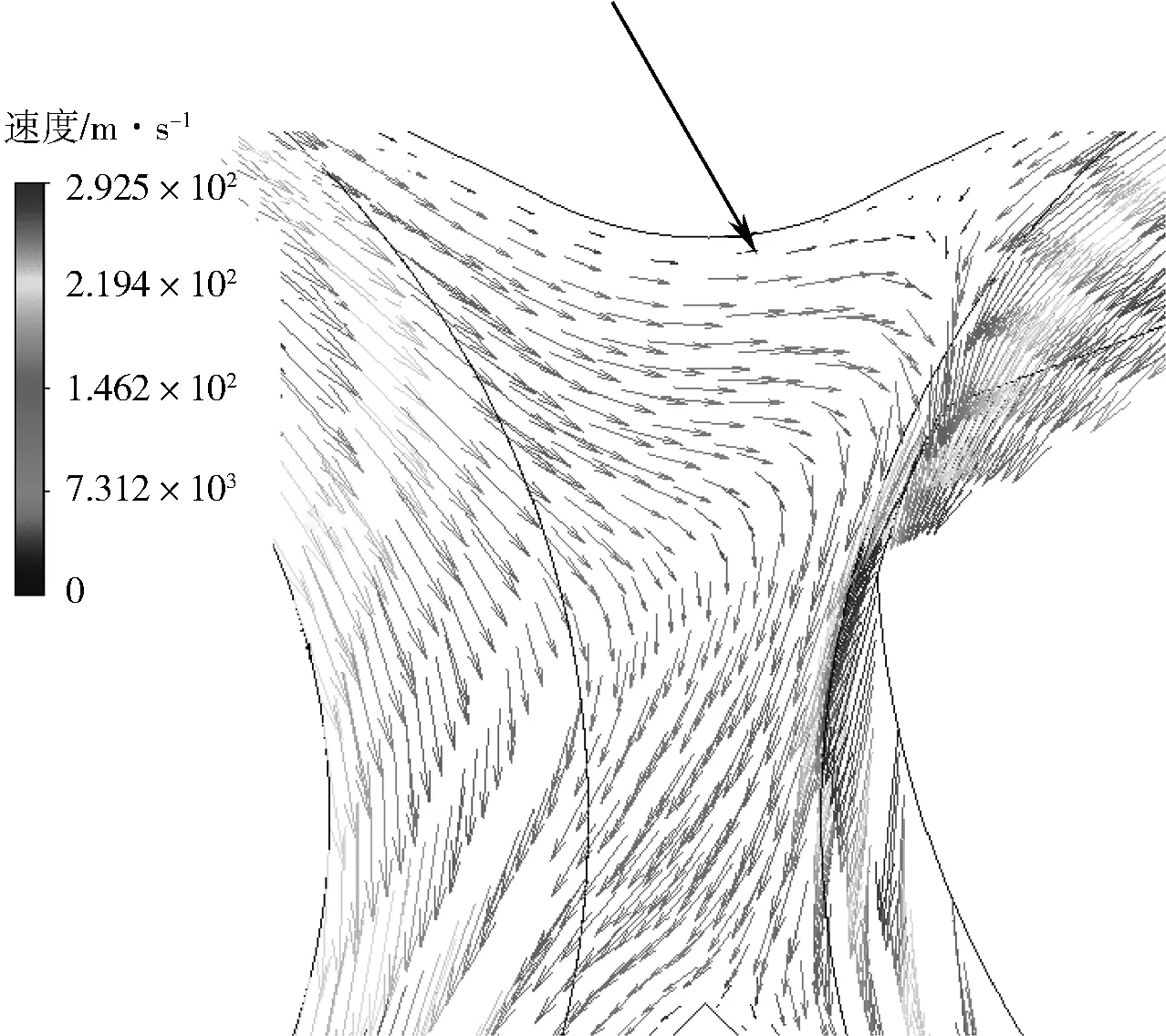
圖8 混煉相互作用窗內的S Smale渦旋Fig.8 S Smale vortex in the interaction window

2.4 PP液滴破碎行為分析

混煉腔中不同位置處流場不同，液滴在不同流場下會發生不同形式的破碎。本模擬中主要觀察到如下3種形式的破碎。

PP液滴在C形區發生的破碎過程的體積分數云圖如圖9所示，圖中，9(b)、9(c)、9(d)和9(e)是圖9(a)液滴位置處的放大圖。由圖中可以看出由于液滴尾部所處剪切場更強，受到的剪切力大，PP液滴不均勻變形為圖9(b)所示的錐狀，尾部變形度比頭部要大很多。當液滴尾部半徑逐漸變小，毛細管數逐漸減小到臨界毛細管數時，便有單個液滴如圖9(e)所示破碎脫落下來。隨著液滴尾部不斷變形，小液滴逐個破碎脫落。

PP液滴在相互作用窗發生的破碎過程的體積分數云圖如圖10所示，圖10(b)、10(c)和10(d)是圖10(a)液滴位置處的放大圖。由圖中可以看出，絲狀液滴在t=1.84 s時破碎成了一系列大小均勻的小液滴。這是由于絲狀液滴在界面張力和剪切力共同作用下，受到輕微擾動后界面不穩定，發生了破碎，稱為毛細不穩現象。擾動是以正弦波的形式在液滴中傳播的，擾動幅度以指數形式增長，當擾動幅度A>0.81R(R為細長線形液滴的半徑)時，絲狀液滴發生破碎[13]。只有當絲狀液滴足夠長時，液滴才會發生毛細不穩破碎，否則液滴通過末端夾斷的方式發生破碎[14]。

PP液滴在螺棱頂部發生的破碎過程的體積分數云圖如圖11所示，圖中11(b)、11(c)、11(d)和11(e)是圖11(a)圓圈位置處的放大圖。可以看出，t=3.13 s時，液滴在螺棱頂部縫隙區受到強剪切，變形度很大。液滴運動到螺棱背風面時進行松弛，如圖11(b)所示。液滴在松弛過程中發生破碎，如圖11(c)所示，最終在t=3.22 s時破碎為3個子液滴。

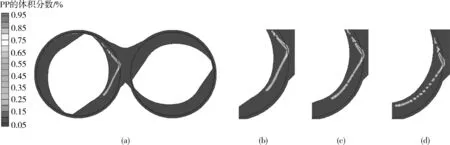
(a)整體圖 (b)t=1.65 s (c)t=1.73 s (d)t=1.84 s圖10 PP液滴在相互作用窗的破碎過程Fig.10 Breakup process of PP droplet at interaction window

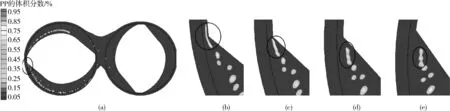
(a)整體圖 (b)t=3.13 s (c)t=3.15 s (d)t=3.18 s (e)t=3.22 s圖11 PP液滴在螺棱頂部的破碎過程Fig.11 Breakup process of PP droplet at rotor tip clearance

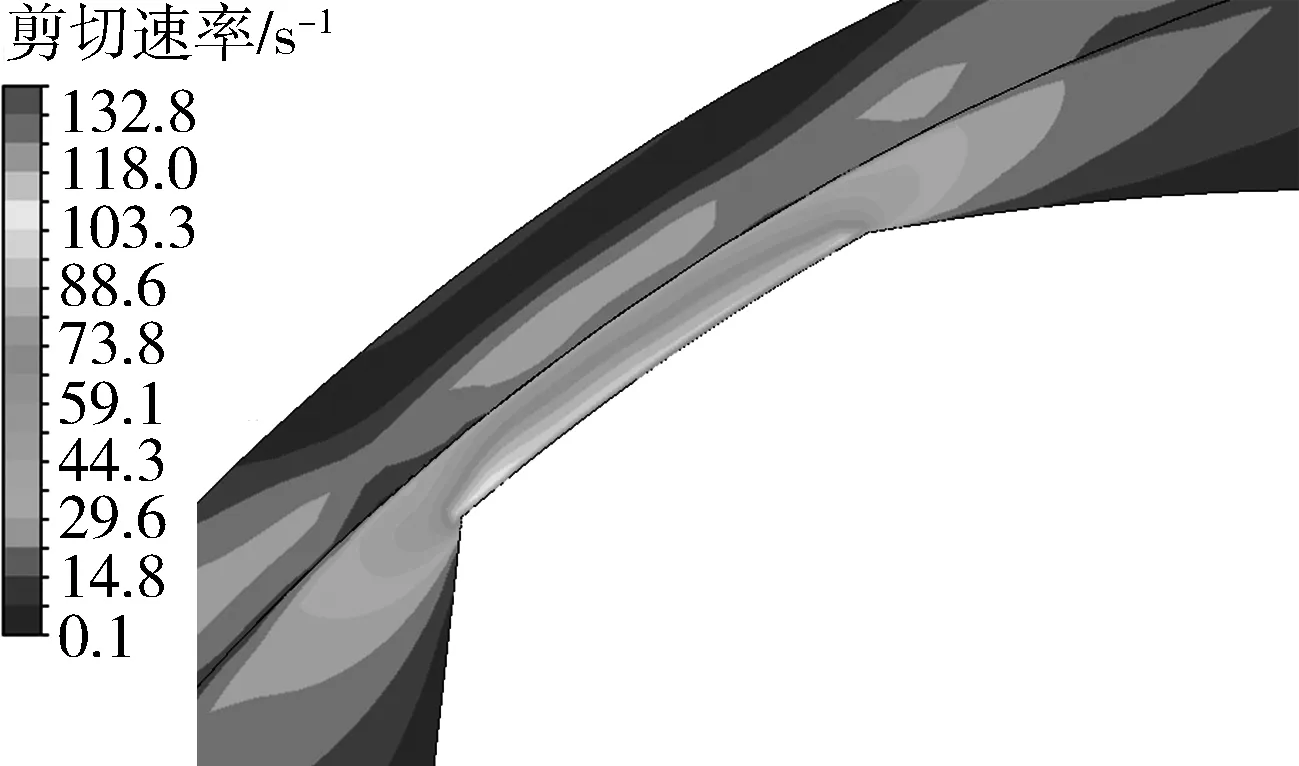
圖12 螺棱頂部間隙區剪切速率分布Fig.12 Contour of shear rate at rotor tip clearance

圖12為螺棱頂部間隙區剪切速率分布。可以看出螺棱頂部剪切速率比其他位置大很多。這是由于螺棱頂部間隙小，同時存在壓力流和拖曳流，速度梯度大，剪切速率大。因此當液滴從螺棱頂部間隙運動到螺棱背風面時，由于剪切速率的突然變小，液滴會發生松弛。當液滴在螺棱頂部間隙區發生足夠大的變形使得液滴半徑足夠小，從而在松弛區毛細管數減小到臨界毛細管數時，液滴會在松弛過程中發生破碎，而未達到臨界毛細管數時，PP液滴在松弛過程中不會發生破碎，只會進行回縮，變形度減小。

2.5 PP液滴二次團聚行為分析

破碎形成的小尺寸液滴在流場中會發生圖13所示的二次團聚過程。圖13為PP液滴的體積分數云圖，其中圖13(b)、13(c)、13(d)和13(e)是圖13(a)圓圈標記處的放大圖。由圖中可以看出，2個小液滴，在流動過程中逐漸接近，發生碰撞，隨后基體相液膜瞬時破碎，液膜逐漸排出，最后2個小液滴團聚為1個大尺寸液滴。

(a)整體圖 (b)t=2.54 s (c)t=2.58 s (d)t=2.61 s (e)t=2.63 s圖13 PP液滴的二次團聚過程Fig.13 Coalescence process of PP droplet

圖14為t=2.54 s時混煉流場的速度分布云圖。可以看出，流場速度繞轉子近似成同心圓分布，靠近轉子處速度較大，靠近壁面處速度最小。小液滴的速度不相同，會進行碰撞，發生二次團聚過程。液滴間的聚并會增大分散相的平均尺寸，最終分散相的尺寸取決于小液滴分散與二次團聚的平衡狀態。

圖14 t=2.54 s時混煉流場的速度分布云圖Fig.14 Contour of velocity at t=2.54 s

3 結論

(1)VOF模型可以用于模擬分散過程中第二相的自由界面，得到熔體液滴的分散演變過程;

(2)PP液滴在C形區發生不均勻變形，這是因為剪切速率近似成同心圓分布，靠近螺棱根部處較小，靠近機筒處較大;

(3)PP液滴在相互作用窗較強的拉伸作用下會發生伸長變形，對液滴的分散非常有利;

(4)PP液滴在螺棱頂部背風處會發生松弛，這是由于在背風處剪切速率迅速變小。當液滴在螺棱頂部強剪切場中變形足夠大使得毛細管數達到臨界毛細管數時，液滴會在松弛過程中發生破碎，否則液滴在松弛過程中只會進行回縮，不發生破碎。

參考文獻：

[1] GI T. The Viscosity of a Fluid Containing Small Drops of Another Fluid[J]. Proceedings of the Royal Society of London. Series A, 1932, 138(834): 41-48.

[2] GAO T,HU H. Deformation of Elastic Particles in Viscous Shear Flow[J]. Journal of Computational Physics, 2009, 228 (6): 2 132-2 151.

[3] LYU S P, BATES F S, MACOSKO C W. Coalescence in Polymer Blends During Shearing[J]. AIChE Journal, 2000, 46 (2): 229-238.

[4] LIN B, SUNDARARAJ U, MIGHRI F,et al. Erosion and Breakup of Polymer Drops under Simple Shear in High Viscosity Ratio Systems[J]. Polymer Engineering & Science, 2003, 43 (4): 891-904.

[5] 劉曉鳴, 謝林生, 馬玉錄，等. 雙轉子連續混煉機轉子混煉段流場的數值研究[J]. 中國塑料, 2006, 20 (11): 95-99.

LIU X M, XIE L S, MA Y L, et al. Numerical Simulation of Flow Fields in the Mixing Section of the Rotor of A Two-rotor Continuous Mixer[J]. China Plastics, 2006, 20(11): 95-99.

[6] 景軍濤, 謝林生, 馬玉錄，等. 轉子結構和工藝參數對雙轉子連續混煉機混合性能的影響[J]. 中國塑料, 2009, 23 (9): 85-90.

JING J T, XIE L S, MA Y L, et al. Influence of Rotor Structure and Technological Parameters on Mixing Performance of A Two-rotor Continuous Mixer[J]. China Plastics, 2009, 23(9): 85-90.

[7] 張 霞, 謝林生,馬玉錄. 雙轉子連續混煉機混煉段拉伸作用的研究[J]. 中國塑料, 2010, 24 (3): 108-113.

ZHANG X, XIE L S, MA Y L, et al. Study on Stretching Effect in Mixing Section of Two-rotor Continuous Mixers[J]. China Plastics, 2010, 24(3): 108-113.

[8] LIU J, LI F, ZHANG L,et al. Numerical Simulation of Flow of Rubber Compounds in Partially Filled Internal Mixer[J]. Journal of Applied Polymer Science, 2015, 132 (35): 42 496.

[9] 葉 萍, 馬玉錄,謝林生. 單個聚合物顆粒在剪切流場中熔融模型的建立[J]. 塑料, 2015, 44 (1): 72-76.

YE P, MA Y L, XIE L S. Establishment of Single Polymer Pellet Melting Process Model Under Shear Flow[J]. Plastics, 2015, 44 (1): 72-76.

[10] 景軍濤, 謝林生, 馬玉錄，等. 雙轉子連續混煉機混合過程的統計學分析[J]. 中國塑料, 2009, 23(2): 93-97.

JING J T, XIE L S, MA Y L, et al. Statistical Analysis on Mixing Process of A Two-rotor Continuous Mixer[J]. China Plastics, 2009, 23(2): 93-97.

[11] 耿孝正. 聚合物加工中固相的分散及填充改性混合設備的選用[J]. 中國塑料, 2002, 16(9): 1-6.

GENG X Z. Dispersion of Solid Phase in Polymer Processing and Choice of Mixing Devices for Filling Modification[J]. China Plastics, 2002, 16(9): 1-6.

[12] WANG W, MANAS-ZLOCZOWER I. Temporal Distributions: the Basis for the Development of Mixing Indexes for Scale-up of Polymer Processing Equipment[J]. Polymer Engineering & Science, 2001, 41 (6): 1 068-1 077.

[13] TOMOTIKA S. On the Instability of a Cylindrical Thread of a Viscous Liquid Surrounded by Another Viscous Fluid[J]. Mathematical and Physical Science, 1935, 150 (870): 322-337.

[14] KOMRAKOVA A E, SHARDT O, ESKIN D,et al. Effects of Dispersed Phase Viscosity on Drop Deformation and Breakup in Inertial Shear Flow[J]. Chemical Engineering Science, 2015, 126: 150-159.