風向對建筑增強型垂直軸風力機氣動性能的影響

朱海天， 郝文星， 李 春， 丁勤衛， 余 萬

(上海理工大學 能源與動力工程學院， 上海 200093)

目前，環境污染與能源緊缺問題日益嚴峻，風能是一種安全且無污染的可再生能源[1]，其開發利用受到世界各國的廣泛關注。隨著風能利用技術的快速發展，風電迅速發展成為世界電能產業愈發重要的組成部分[2-3]。風力機是一種將風的動能轉化為電能的旋轉機械。目前，風力機組主要安裝于遠離城市負荷中心的風資源集中區域，由于當地電網接納能力、跨區輸電能力以及應對風速隨機性和間歇性能力的不足，棄電限電現象較為嚴重[4]。2014年，中國平均風電棄風率約為8%，2015年則高達18.6%[5]。

為減緩棄電限電現象的發生，Keirstead等[6]指出，近年來各種與建筑物結合的部分風力機被應用于城市中，包括適用于多場合的微型風力機、安裝于樓頂的風力機以及垂直軸阻力型風力機等，這種風能利用形式避免了輸、送電能問題，產生的電能可直接用于建筑本身，為解決城市能源緊缺問題和棄電限電問題提供了技術支持。因此，充分利用建筑環境中的風能為風電發展提供了一種新思路。較之郊區和偏遠地區，城市來流風具有平均風速低和湍流度大等特點，由于建筑物的影響，也存在局部大風區域[7]。

風力機與建筑物結合的形式基本可分為3類：安裝于建筑頂部的風力機、安裝于建筑物中央的風力機及建筑增強型風力機(BAWT)[8]。1930年， Honnef首先提出了建筑增強型風力機概念設計。建筑增強型風力機將風力機與建筑相結合，利用建筑對風能的強化和集結作用，從而提高發電效率[9]。2008年底，巴林世界貿易中心完工[10]，在雙子塔建筑之間加裝了3個直徑為29 m的建筑增強型水平軸風力機，這是世界上第一座大型結合風力渦輪的建筑。Li等[11]對珠江大廈空洞中安裝垂直軸風力機(VAWT)的效益進行實驗評估，結果表明喇叭口型洞口將增強風速，受風向和周圍建筑物的影響較為明顯。Heo等[12]對建筑增強型水平軸風力機進行了數值計算，結果表明建筑擴散體可大幅提升發電效率，但該種BAWT受風多向性差，當偏航角小于30°時才具有較高的電能輸出。

上述研究一部分利用大氣邊界層風剪切效應，充分利用高層建筑的高度優勢捕獲更多的風能，另一部分利用建筑周圍的局部大風。其中風剪切是指風速隨高度變化[13]，主要受地面粗糙度和科利奧效應影響。筆者提出一種風力機新型安裝方式與安裝位置，將VAWT懸掛固定于建筑擴散體間的懸臂梁下端，利用上述2種優勢對建筑環境中VAWT進行研究。

直線翼垂直軸風力機(SB-VAWT)是最具代表性[14]的垂直軸風力機之一。SB-VAWT在旋轉時具有極復雜的氣動特征[15-16]：一方面，攻角周期性大幅變化導致SB-VAWT氣動載荷波動較大且直葉片周圍流場結構非常復雜；另一方面，單制動槳盤假設已不適用于SB-VAWT，應采用雙制動槳盤假設，因此下游尾跡區易受到上風區脫落渦軌跡的影響，而且葉片尾跡、主軸尾跡與及葉片支撐桿尾跡之間也發生相互作用，從而加劇流動的復雜性。因此，研究建筑擴散體間SB-VAWT的氣動性能十分必要。

筆者采用計算流體力學(CFD)方法對原始SB-VAWT進行數值研究，并與實驗值進行對比，驗證了該網格拓撲結構及Realizablek-ε湍流模型的適用性。以上海風資源特點作為研究條件，研究風向對建筑增強型直線翼垂直軸風力機(BASB-VAWT)性能與流場結構的影響，得到其氣動特性，以期為不同城市中采用BASB-VAWT提供依據。

1 氣動理論

1.1 建筑環境中風能利用特點

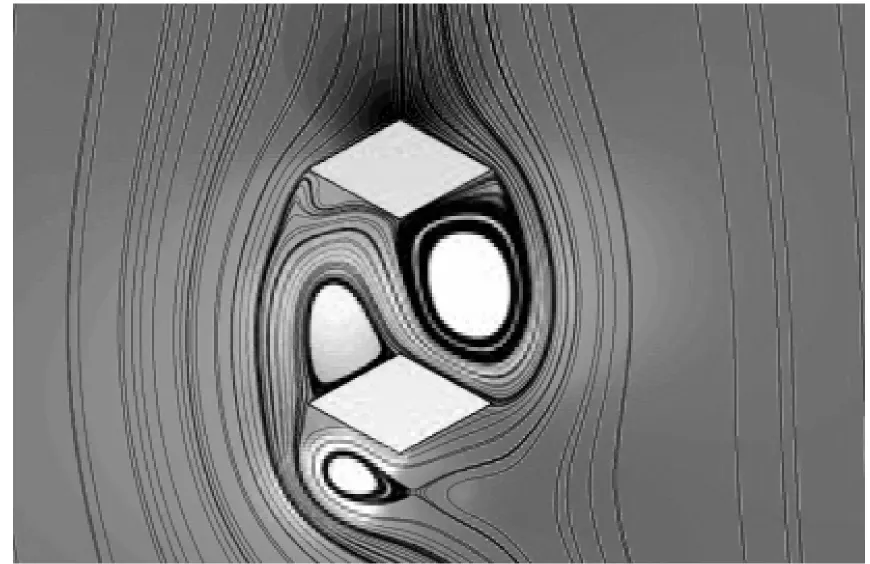
圓形截面建筑擴散體周圍風場CFD模擬結果如圖1所示。由于“夾道效應”，2座建筑物間的風速增大，形成局部強化風[13]。

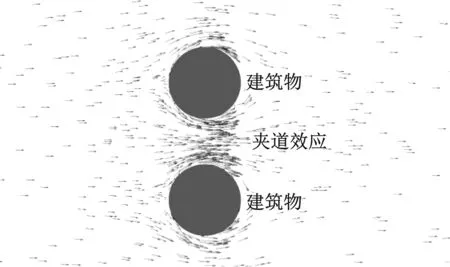
圖1 圓柱體建筑物之間的夾道效應

1.2 風剪切

風剪切效應是指風速隨海拔高度增加而增大，要利用高層建筑的高度優勢就必須考慮城市中的風剪切效應，筆者采用以下指數模型：

V/V0=(H/H0)β

(1)

式中：H為地面高度；H0為地面參考高度；V為H處的風速；V0為H0處某參考點的風速；β為切變系數，該系數與大氣穩定度和地面粗糙度有關，其值如表1所示[17]。

表1 中國地面粗糙度類別與對應的β值

采用地面粗糙度類別為D的經驗指數模型來描述上海市市區平均風速沿高度的變化規律。上海市年平均風速為3.65 m/s，根據風剪切效應可知，200 m高空處的城市來流風速為9 m/s。

1.3 主要氣動參數

在SB-VAWT中赤道平面攻角α隨相位角的周期性變化關系如下：

(2)

式中：θ為相位角；λ為葉尖速比。

葉尖速比定義為葉尖切向速度與來流風速的比值：

(3)

式中：ω為角速度；V∞為來流風速；R為旋轉半徑。

力矩系數Cm與風能利用系數Cp均是衡量VAWT性能的重要指標。

(4)

式中：T為轉矩；P為風力機功率；ρ為空氣密度；A為掃風面積。

實度σ作為描述SB-VAWT幾何形狀的重要無因次參數，其表達式[1]如下：

σ=Nc/(2R)

(5)

式中：N為葉片數；c為翼型弦長。

2 計算模型

2.1 幾何模型

采用對低雷諾數工況有較高風能利用系數的NACA0021對稱翼型[18]，其弦長c為85.8 mm，最大厚度為0.21c，最大厚度位置在0.3c處，翼型幾何模型見圖2。

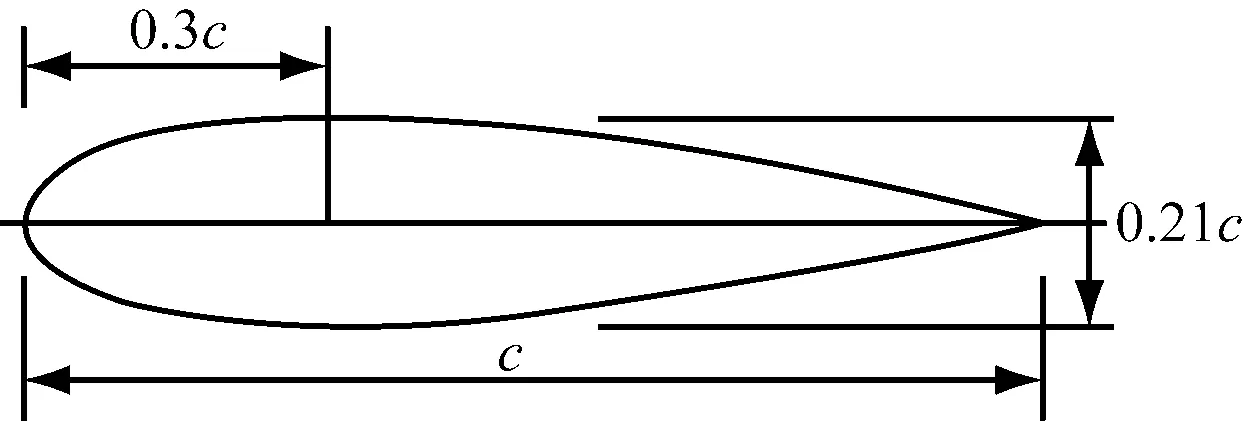
圖2 翼型幾何模型

為與實驗值進行比較，采用的幾何模型參數均與文獻[19]相同。SB-VAWT幾何參數見表2。

巴林世界貿易中心的建筑增強型水平軸風力機實圖與本文BASB-VAWT幾何模型的對比如圖3所示。其中建筑增強型水平軸風力機放置于懸臂梁前端，而BASB-VAWT垂直懸掛于懸臂梁下端。

2.2 計算域結構及網格分布

SB-VAWT與翼型周圍計算域結構及網格分布如圖4所示。SB-VAWT遠場計算域結構由半圓形上游區與矩形下游尾跡區組成，如圖4(a)中上游區特征長度為50R，下游尾跡區特征長度為30R。SB-VAWT近場計算域結構由Z1和Z22個網格域構成，Z1為靜止結構網格域，Z2為滑移非結構網格域。翼型周圍計算域結構也由半圓形上游區與矩形下游尾跡區組成，如圖4(b)與圖4(c)所示。上游區特征長度為0.5R，下游尾跡區特征長度為0.3R，翼型周圍網格域共分為6個域,如圖4(d)所示。域1和域6分別為翼型前緣域和翼型后緣域。定義SB-VAWT計算域中的半圓和矩形上下邊界ad與bc速度入口邊界條件，來流風速為9 m/s，矩形右邊界cd為壓力出口條件。

表2 SB-VAWT幾何參數

(a) 巴林世界貿易中心

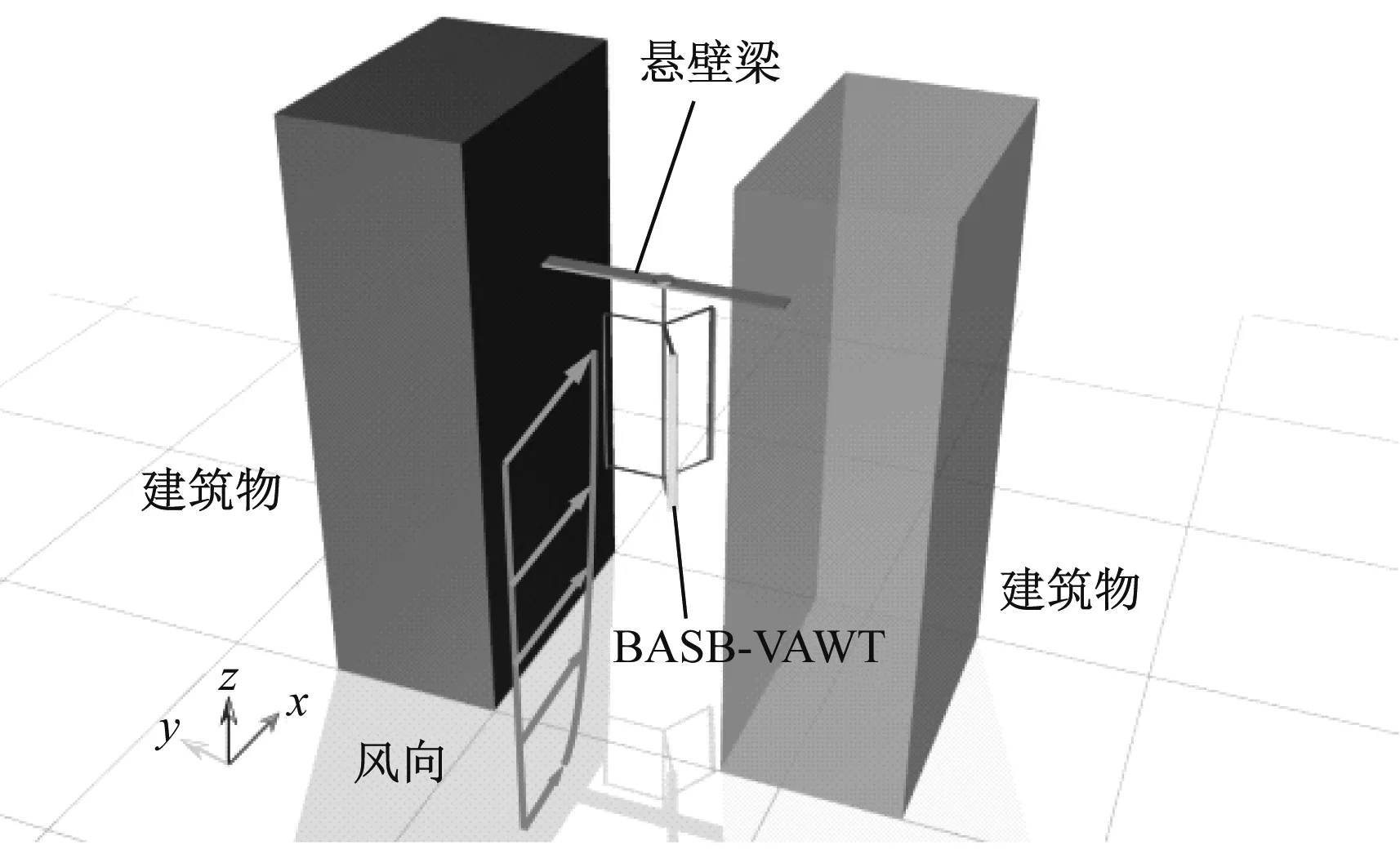
(b) BASB-VAWT實體圖

(c) BASB-VAWT側視圖

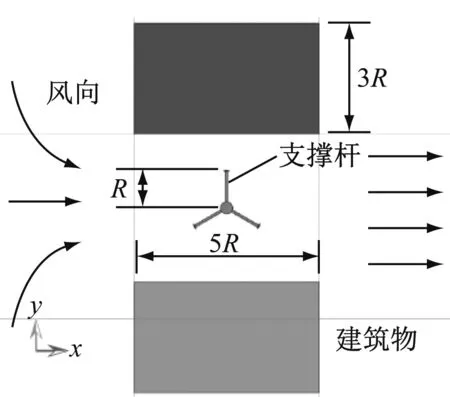
(d) BASB-VAWT俯視圖

(a) 遠場拓撲結構示意圖(b) 二維簡化圖

(c) 遠場計算域網格分布(d) 翼型周圍計算域結構

(e) 近場計算域網格分布(f) 翼型周圍網格分布

圖4 計算域結構及網格分布

Fig.4 Calculation region and mesh distribution of the airfoil

SB-VAWT遠場計算域結構網格分布如圖4(c)所示，Z1和Z2近場計算域混合網格分布如圖4(e)所示。翼型表面布置250個網格節點，并對翼型周圍進行加密處理，由翼型表面到遠場邊界方向布置70個節點，如圖4(f)所示。總網格數為421 092。

采用Realizablek-ε湍流模型，在模擬旋轉流動方面該湍流模型優于Standardk-ε湍流模型，也能較精確地捕捉到流動分離點[20]。y+值接近30～100才能使壁面函數較好地捕捉到邊界層的流動[21]。故本文網格模型選取的y+在30～50內。

2.3 網格無關性驗證

BASB-VAWT網格無關性驗證結果見表3。以大網格數約66萬計算結果為基準，結果表明：在約42萬總網格數時的計算值與約66萬總網格數時的計算值偏差較小，故本網格模型是可信的。因此，選取約為42萬網格數的模型作為最終計算模型。

表3 網格無關性驗證結果

2.4 實驗驗證

原始SB-VAWT二維風能利用系數Cp計算值與實驗值[19]的對比如圖5所示。由圖5可知，在低葉尖速比時，風能利用系數計算值與實驗值的差值略大，其主要原因有：(1) 文獻[19]中的實驗值未考慮風洞阻塞效應且未排除轉軸與力矩傳感器間的摩擦阻力力矩；(2) 筆者僅考慮二維SB-VAWT，即設為無限長葉片，然而Li等[22]指出，二維SB-VAWT計算值相比三維SB-VAWT計算值與實驗值具有較大差值，這是由于二維SB-VAWT葉片未考慮沿展向葉素表面壓差逐漸降低的因素；(3) 二維SB-VAWT未考慮葉片支撐桿對SB-VAWT的影響。

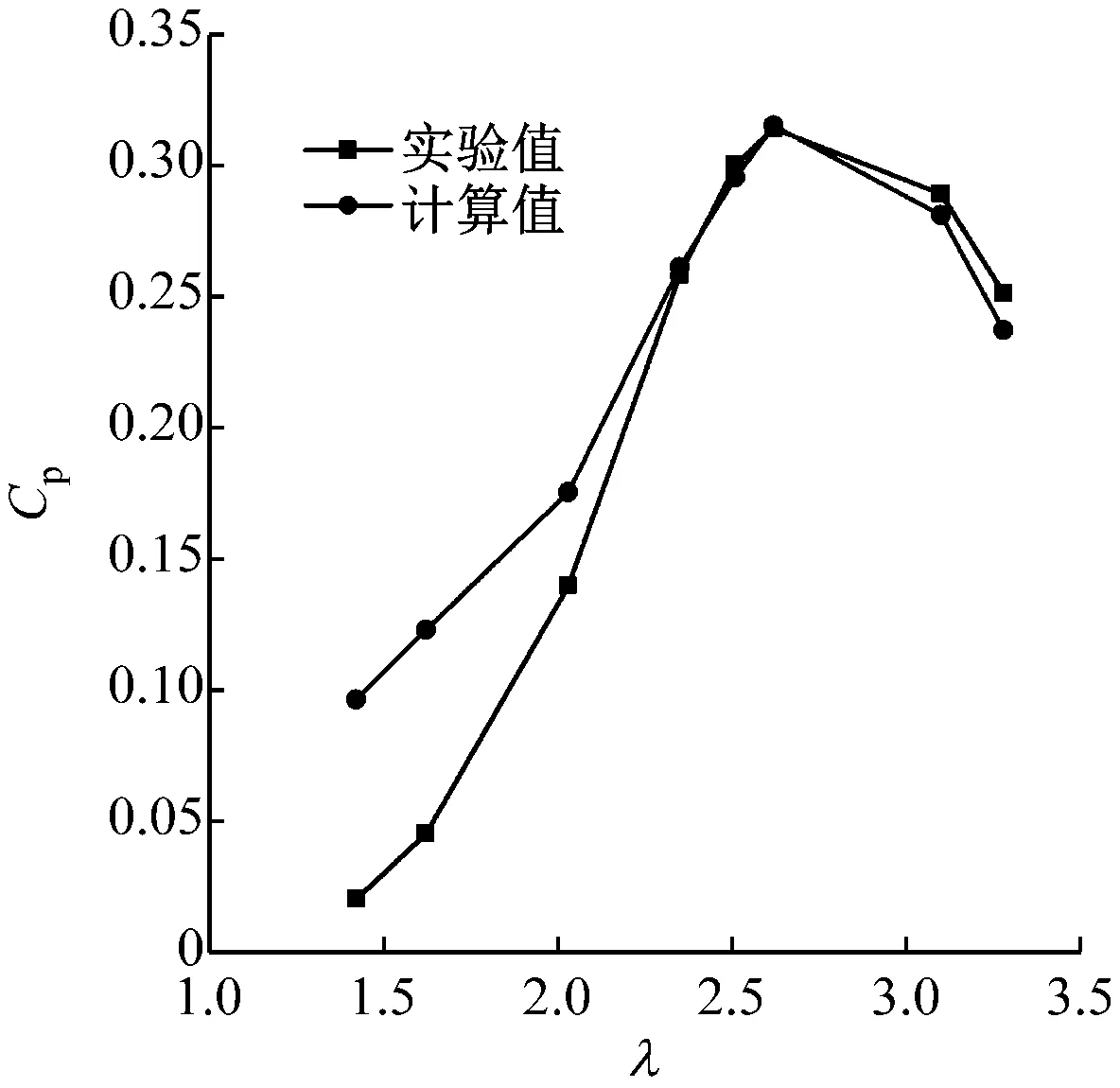
圖5 二維風能利用系數計算值與實驗值的對比圖

結合上述3種降低風能利用系數的實際因素，故本文二維CFD計算值與實驗值存在誤差，但本文CFD計算值仍可捕捉到最大風能利用系數對應的最佳葉尖速比，其值為2.62。因此，二維CFD計算值仍可定性且定量地反映風向對不同BASB-VAWT的影響。

2.5 風玫瑰圖

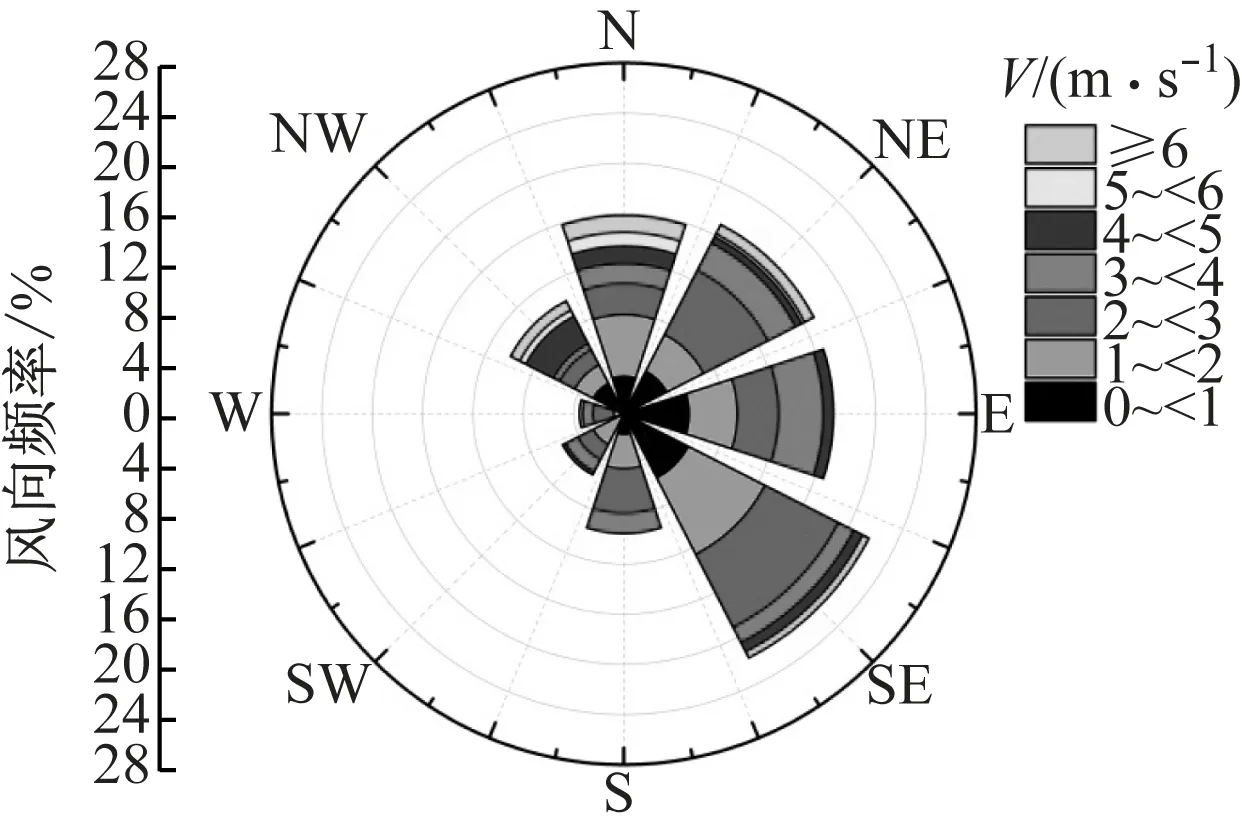
以上海市近3年天氣報告作為風向研究條件，如圖6所示共8個風向，包括北風(N)、東北風(NE)、東風(E)、東南風(SE)、南風(S)、西南風(SW)、西風(W)及西北風(NW)。其中，縱軸代表出現此風向的頻率。

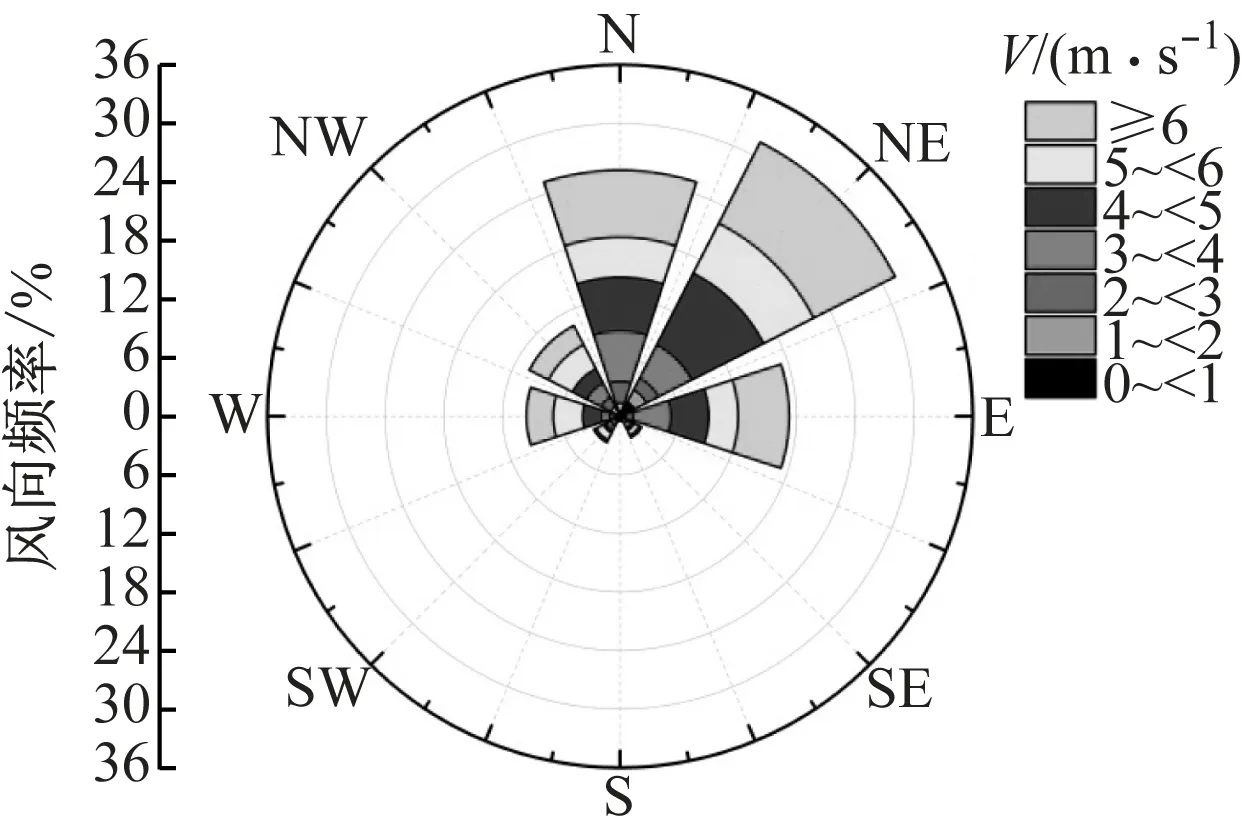
(a) 2014年

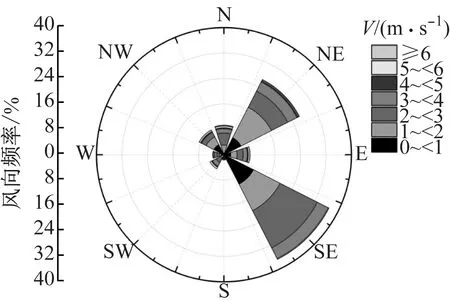
(b) 2015年

(c) 2016年

由圖6可知，上海市東南風、東風及東北風工況頻數較多，近3年平均風速為3.65 m/s。

2.6 建筑擴散體型

將建筑擴散體截面分為4種：正圓形、橢圓形、矩形及菱形。幾何模型如圖7所示，由于4種建筑擴散體均為中心點對稱模型，故僅需研究3種不同風向下的工況：與建筑擴散體對稱軸平行的風向、與建筑擴散體對稱軸之間角度呈45°的風向以及與建筑擴散體對稱軸垂直的風向，因而工作量大大降低。因需要引入氣象資料，故將這3種風向分別稱為西風、西北風及北風，如圖7所示的方向位置。

正圓形擴散體SB-VAWT周圍局部流場網格分布如圖8所示。其他BASB-VAWT的周圍流場網格分布不再贅述。

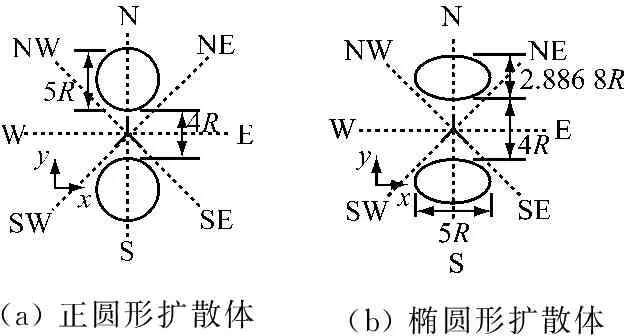
(a) 正圓形擴散體(b) 橢圓形擴散體

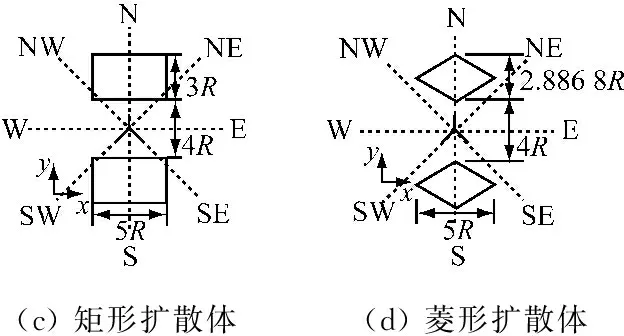
(c) 矩形擴散體(d) 菱形擴散體

圖7 4種建筑擴散體

Fig.7 Four models of the building diffuser

圖8 正圓形擴散體BASB-VAWT網格分布局部放大圖

3 結果與分析

3.1 BASB-VAWT周圍流場分析

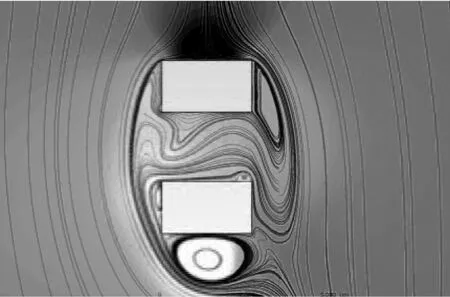
圖9和圖10為各風向下建筑擴散體的壓力云圖、流線圖和BASB-VAWT速度云圖，其中來流風速為9 m/s。

由圖9可知，建筑前后壓差造成局部大風區域，建筑外廓使一部分流體集聚于兩建筑之間。在西北風工況下，矩形擴散體間建筑產生的大流動分離發展至大部分流道中，而其他截面擴散體間建筑產生的渦流并沒有大幅發展至流道中。在北風工況下，流場結構極為復雜，建筑背風面存在大分離渦。

根據最佳捕獲風能的位置安裝BASB-VAWT。在西風工況下，建筑擴散體間的風速明顯大于入口風速，風力機可捕獲更多的風能。在西北風工況下，由于建筑擴散體產生的流動分離部分發展至風力機旋轉區域內，對風力機產生一定影響。在北風工況下，由于建筑擴散體間的風速較低，且建筑背風面存在大分離渦，風力機將承受更劇烈的載荷波動。

西風西北風

北風

西風西北風

北風

西風西北風

北風

西風西北風

北風

3.2 BASB-VAWT氣動性能分析

考慮BASB-VAWT在不同建筑擴散體下不同風向工況時的性能，對西風、西北風及北風工況時BASB-VAWT一個旋轉周期內的周圍流場進行數值模擬，其λ為2.62。BASB-VAWT風能利用系數計算結果如圖11所示。

由圖11可知，在西風工況下，正圓形BASB-VAWT風能利用系數較高，其值為0.783 30，風能利用系數提升至原始SB-VAWT的2.47倍；橢圓形BASB-VAWT風能利用系數較低，為0.678 73；在西北風工況下，正圓形BASB-VAWT風能利用系數較高，其值為0.389 20；菱形BASB-VAWT風能利用系數較低，為0.286 96；在北風工況下，由于建筑擴散體之間風速過低，風力機效率極低。

為進一步得到風向對BASB-VAWT年風能利用系數的影響，結合上海市近3年風玫瑰圖，通過加權平均得出BASB-VAWT年風能利用系數，如圖12所示。其中，在北風工況下，4種BASB-VAWT年風能利用系數均較低，且葉片周圍流場極為復雜，故年風能利用系數并未考慮北風工況。同理，在西北風工況下，矩形擴散體自身的強渦流直接影響風力機的葉片，故在研究年風能利用系數中并未考慮此工況。

由圖12可知，在上海市市區，正圓形BASB-VAWT具有較高的年風能利用系數，近3年其均值為0.385 92；而矩形BASB-VAWT年風能利用系數較低，近3年其均值為0.140 48。

為進一步研究BASB-VAWT在西風及西北風工況下的載荷波動，對4種BASB-VAWT進行了對比分析，由于北風工況下的流場結構復雜，故對其力矩系數進行研究無意義。BASB-VAWT力矩系數與相位角θ的關系見圖13。

西風西北風

北風

西風西北風

北風

西風西北風

北風

西風西北風

北風

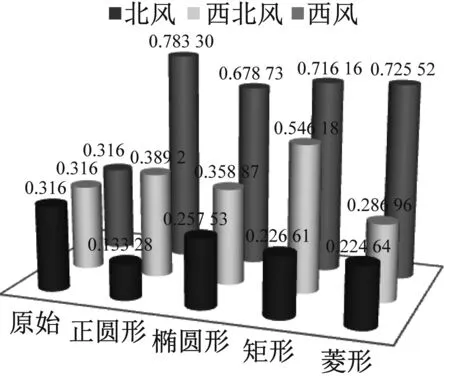
圖11 BASB-VAWT風能利用系數

由圖13可知，在西風工況下，BASB-VAWT將承受比原始SB-VAWT更大幅的載荷波動。在西北風工況下，矩形BASB-VAWT的載荷波動較原始SB-VAWT與其他擴散體BASB-VAWT的載荷波動更為劇烈，正圓形、橢圓形BASB-VAWT與原始SB-VAWT曲線相近。而菱形BASB-VAWT的性能較差，這是由于在菱形擴散體間形成局部大風區域較為滯后。

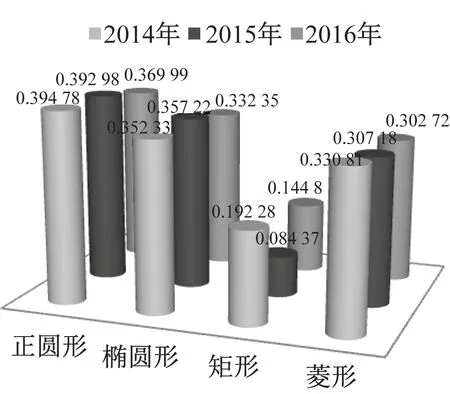
圖12 BASB-VAWT年風能利用系數

4 結 論

(1) BASB-VAWT氣動性能對風向敏感，在西風工況下，其性能大幅提升；在西北風工況下，性能稍高于原始SB-VAWT；在北風工況下，流場結構非常復雜且建筑產生的脫落渦發展至風力機旋轉半徑內，其性能遠低于原始SB-VAWT。

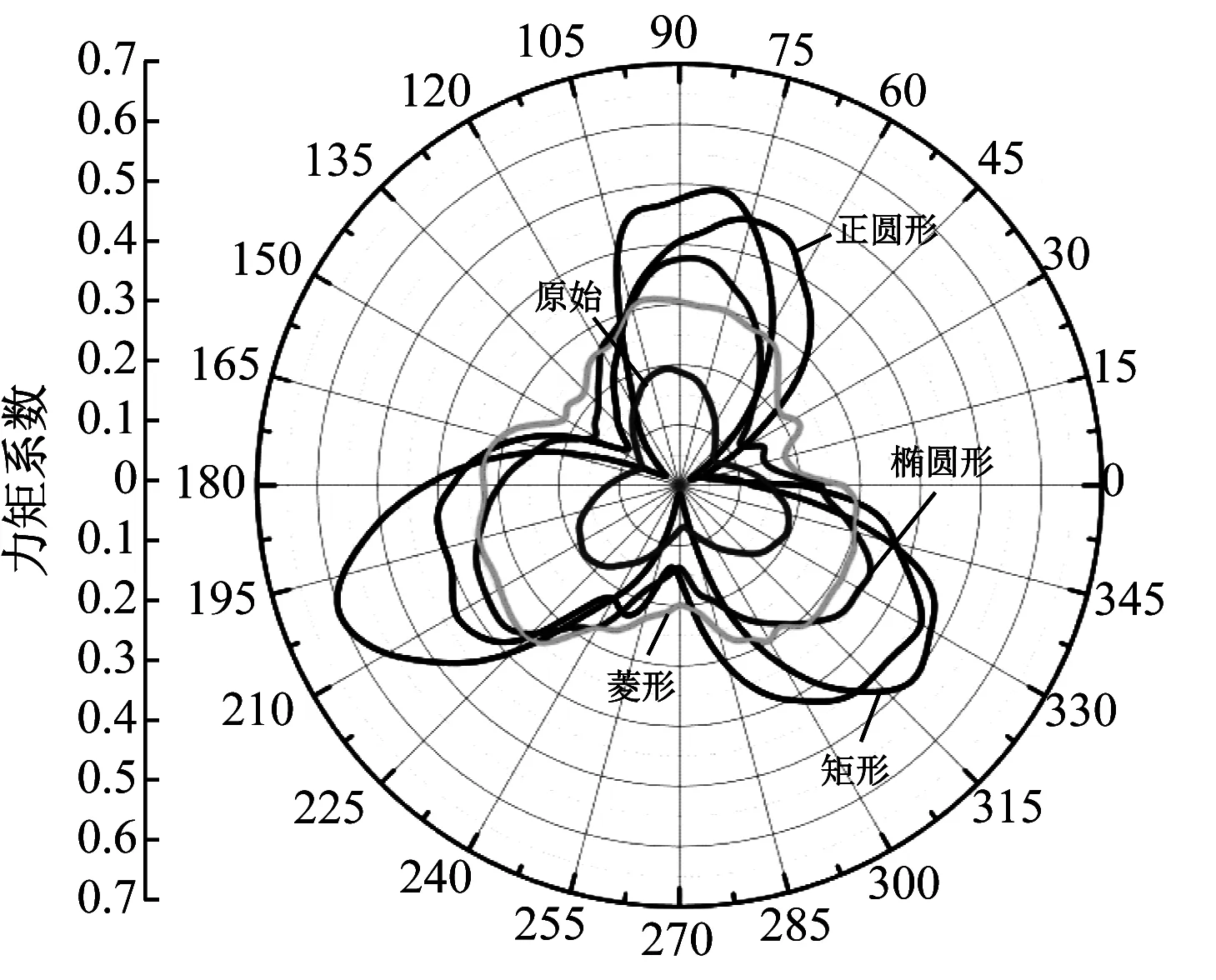
(a) 西風工況下

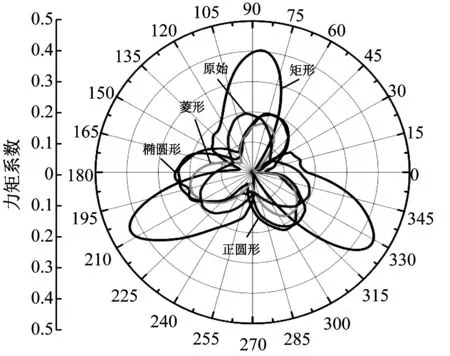
(b) 西北風工況下

(2) BASB-VAWT氣動性能對建筑擴散體排布及建筑平面外廓敏感，較之橢圓形和正圓形建筑，矩形建筑的風力機性能較劣，而正圓形建筑優于長半軸平行于風向的橢圓形建筑。

參考文獻：

[1] 李春, 葉舟, 高偉, 等. 現代大型風力機設計原理[M]. 上海: 上海科學技術出版社, 2013.

[2] 王東華, 葉舟, 郝文星, 等. 海上漂浮式風力機Spar平臺波頻與慢漂響應性能分析[J].動力工程學報, 2016, 36(11): 907-913.

WANG Donghua, YE Zhou, HAO Wenxing, et al. Analysis on wave frequency and slow drift response of a Spar platform for offshore floating wind turbines[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(11): 907-913.

[3] SCHEURICH F, FLETCHER T M, BROWN R E. Simulating the aerodynamic performance and wake dynamics of a vertical-axis wind turbine[J].WindEnergy, 2011, 14(2): 159-177.

[4] 國家能源局. 關于做好2013年風電并網和消納相關工作的通知[R]. 北京：國家能源局，2013.

[5] 李俊峰, 蔡豐波, 喬黎明, 等. 2015年中國風電發展報告[R]. 北京: 中國循環經濟協會可再生能源專業委員會, 2015.

[6] KEIRSTEAD J, JENNINGS M, SIVAKUMAR A. A review of urban energy system models: approaches, challenges and opportunities[J].RenewableandSustainableEnergyReviews, 2012, 16(6): 3847-3866.

[7] 姜瑜君, 桑建國, 張伯寅. 高層建筑的風環境評估[J].北京大學學報(自然科學版), 2006, 42(1): 68-73.

JIANG Yujun, SANG Jianguo, ZHANG Boyin. An evaluation on wind environment around skyscrapers[J].ActaScientiarumNaturaliumUniversitatisPekinensis, 2006, 42(1): 68-73.

[8] MULLER G, JENTSCH M F, STODDART E. Vertical axis resistance type wind turbines for use in buildings[J].RenewableEnergy, 2009, 34: 1407-1412.

[9] HEYMANN M. Signs of hubris: the shaping of wind technology styles in Germany, Denmark, and the United States, 1940-1990[J].TechnologyandCulture, 1998, 39(4): 641-670.

[10] 袁行飛, 張玉. 建筑環境中的風能利用研究進展[J].自然資源學報, 2011, 26(5): 891-898.

YUAN Xingfei, ZHANG Yu. Progress in the study of wind energy utilization in the built environment[J].JournalofNaturalResources, 2011, 26(5): 891-898.

[11] LI Q S, SHU Z R, CHEN F B. Performance assessment of tall building-integrated wind turbines for power generation[J].AppliedEnergy, 2016, 165: 777-788.

[12] HEO Y G, CHOI N J, CHOI K H, et al. CFD study on aerodynamic power output of a 110 kW building augmented wind turbine[J].EnergyandBuildings, 2016, 129: 162-173.

[13] GUALTIERI G. Atmospheric stability varying wind shear coefficients to improve wind resource extrapolation: a temporal analysis[J].RenewableEnergy, 2016, 87: 376-390.

[14] LI Qing'an, MAEDA T. Study on flow around straight-bladed vertical axis wind turbine under low tip speed ratio[J].JournalofFluidScienceandTechnology, 2014, 9(3): JFST0051.

[15] MOHAMED M H. Impacts of solidity and hybrid system in small wind turbines performance[J].Energy, 2013, 57: 495-504.

[16] XIAO Qing, LIU Wendi, INCECIK A. Flow control for VATT by fixed and oscillating flap[J].RenewableEnergy, 2013, 51: 141-152.

[17] 中華人民共和國建設部. 建筑結構荷載規范(2006版): GB 50009—2001[S]. 北京: 中國建筑工業出版社, 2002.

[18] MOHAMED M H. Performance investigation of H-rotor Darrieus turbine with new airfoil shapes[J].Energy, 2012, 47: 522-530.

[19] CASTELLI M R, ARDIZZON G, BATTISTI L, et al. Modeling strategy and numerical validation for a Darrieus vertical axis micro-wind turbine[C]//Proceedingsof2010InternationalMechanicalEngineeringCongressandExposition. Vancouver, Canada: British Columbia, 2010.

[20] LI Qing'an, MAEDA T, KAMADA Y, et al. Wind tunnel and numerical study of a straight-bladed vertical axis wind turbine in three-dimensional analysis (part Ⅱ: for predicting flow field and performance)[J].Energy, 2016, 104: 395-307.

[21] STOLARSKI T, NAKASONE Y, YOSHIMOTO S. Engineering analysis with ANSYS software[M]. Amsterdam, Holland: Butterworth-Heinemann, 2007.

[22] LI Qing'an, MAEDA T, KAMADA Y, et al. Wind tunnel and numerical study of a straight-bladed vertical axis wind turbine in three-dimensional analysis (part I: for predicting aerodynamic loads and performance)[J].Energy, 2016, 106: 443-452.