雙通道旋轉變壓器粗精組合軸角轉換原理及應用

趙文香，劉玉晶，張 巍，馬立明

(北方導航控制技術股份有限公司，北京 100176)

目前，旋轉變壓器作為測角元件應用很廣，在武器系統中主要應用于測量車體的姿態角、高低角和方位角。在以數字化戰場為核心的系統中，要想充分發揮作戰效能，必須提高命中率和快速反應能力；因此，提高各個傳感器的輸出精度尤為關鍵。旋轉變壓器以及相應的數字變換器具有較高的可靠性和抗干擾能力，良好的環境條件適應性和可維護性，近十年來，各種用途的火控系統都采用了旋轉變壓器做為測角、數據傳輸和同步控制等[1]。提高測量精度有2種方式：一種是多極旋轉變壓器可以提高固有精度；另一種是用2種不同極對數的旋轉變壓器組成組合電動機，利用提高傳動比來提高測量精度。

目前的旋轉變壓器大多采用粗精組合來提高其精度，粗精組合時的糾錯問題是粗精組合系統的一個關鍵問題。

1 雙通道旋轉變壓器粗精組合軸角轉換原理及糾錯方法

1.1 粗精組合轉換原理

雙通道旋轉變壓器是由2種不同極對數的旋轉變壓器組成一體的組合電動機。粗通道多選用單極旋轉變壓器，精通道選用多極旋轉變壓器。粗精組合原理如圖1所示。以前傳動比多為20～30，現在傳動比已提高，如32、64和128等。

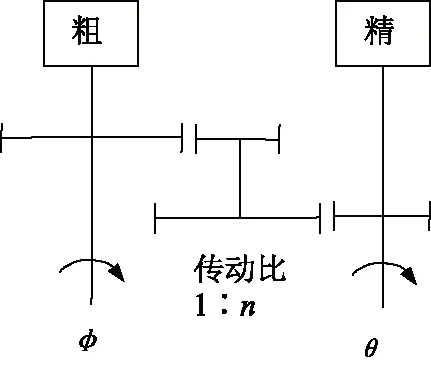
圖1 粗精組合原理圖

粗精組合系統的意義表現在2個方面：一是以增加元件為代價，來換取較高的測量精度，而對元件本身的精度并沒有更高的要求， 這就克服了元件制

造工藝水平的限制；二是可以利用2個精度等級較差的旋轉變壓器和變速箱來代替1個高精度的旋轉變壓器，以完成高精度的角度測量[2-4]。

粗精組合的基本思想是利用放大n后測量，來達到提高精度的目的。為了提高測角精度，旋轉變壓器采用多級旋轉變壓器，由旋轉變壓器輸出電壓公式可計算出相應的粗測角度φ和精測角度θ。將粗精解算結果φ、θ分別用10位和14位二進制表示，粗精組合關系如圖2所示。

圖2 粗精組合關系圖

1.2 粗精組合糾錯方法

為了提高旋轉變壓器的精度(分辨率)，研制出了高精度的多極旋轉變壓器。對于多極旋轉變壓器來說，其工作原理與單極旋轉變壓器完全相同，只是輸出電壓的有效值隨轉子轉角變化的周期不同。

多極旋轉變壓器的粗精組合是利用放大n來提高測角精度；但應保證粗讀整數不能有差錯，因為一旦粗讀整數有錯，精讀小數再準確也是無意義的。粗軸與精軸之間是靠傳動比聯系的，而粗精兩通道的讀數彼此是獨立的。由于種種原因，例如傳動誤差、旋轉變壓器誤差、編碼電路的誤差，以及測角元件和轉換器的誤差不可能完全匹配等，實際得不到粗精兩通道重合位讀數的理想配合，這種誤差發生于粗讀整數在2個刻度的邊界狀態下，有可能使粗通道的最低有效位多計或少計1個數，因此，應對粗通道的最低有效位進行糾錯。

糾錯方法按如下3種情況進行，它的基本思想是以精位數碼為準來校正粗位數碼，以粗位與精位的重合位進行比較鑒別，完成糾錯。

1)精角寄存器的角度在第1象限(θ<90°)時，粗角寄存器只能少記，不可能多記，根據精角寄存器的第1、第2位和粗角寄存器的第7、第8位的狀態，考慮向粗角寄存器的第6位進1。

2)精角寄存器的角度在第4象限(270°<θ<360°)時，粗角寄存器只能多記，不能少記，考慮向粗角寄存器的第6位減1。

3)精角寄存器的角度在第2或第3象限時，粗角寄存器既不會多計，也不會少計，這時不必進行糾錯。

1.3 粗精組合傳動比的選擇

多級旋轉變壓器測角精度高是因為它本身的精度高，并且N對極旋轉變壓器將單極旋轉變壓器的電角度偏差由θ增加到Nθ，提高了小失調角時的輸出電壓，相當于增大了小失調角時系統的開環放大倍數，根據控制理論，這樣會明顯減小系統誤差。

無限制提高旋轉變壓器的極對數，給制造上帶來較大的困難，如果N>8，在制造上基本不可能了。為了進一步提高旋轉變壓器的精度(分辨率)，往往采用雙通道的旋轉變壓器組合。

在實際工程系統中，往往需要機械粗精嚙合旋轉變壓器系統輸出數字化，以便得到表示軸角的單值數字。這類要求常常越來越多地由電器嚙合的旋轉變壓器系統來實現。因為2類系統包含有相同的技術和粗精系統機電方面的相關信息。

如果利用10位旋轉變壓器/數字變換器組成的雙通道系統，選擇粗精之間的傳動比為1∶64，即可把精度從10位提高為20位，因為傳動比為1∶64，精通道旋轉變壓器旋轉1周，而粗通道旋轉變壓器轉角為5.625°。

按照武器系統測角的精度和分辨率要求來選定傳動比，如已知精通道轉換器為14位，系統需要的分辨率為18位，即需要提高4位，則傳動比為1∶16。上述解算是由計算雙通道系統的分辨率的方法反推導而得到的。

按照上述步驟，可以計算出本系統在精轉換器為14位、系統分辨率為20位時傳動比為1∶64。

2 應用設計

2.1 硬件電路設計

為了適應武器裝備系統的計算機控制，需要將旋轉變壓器輸出的四線交流信號轉換成數字量。粗精組合糾錯邏輯電路圖如圖3所示。表征軸角θ的四線交流輸出電壓，直接輸入粗、精旋轉變壓器/數字轉換器轉換成粗、精數據，再輸入單片機，單片機進行數據糾錯和處理后即可得表征軸角θ的20位數字，計算機接收上述數字量進行適時控制[5]。

圖3 粗精組合糾錯邏輯電路圖

2.2 粗精組合糾錯程序設計

該部分軟件設計主要是處理數據采集程序采集到的數據，組合糾錯后，輸出真實角度值。采用的方法是對粗、精通道輸出數字重合位的電平狀態進行邏輯判斷，這一方法通常稱之為余數比較法。應根據粗、精通道之間的相對誤差(應把它看成是粗通道的誤差)的大小來決定需要多少個重合位才能判斷有無模糊誤差。當粗通道的誤差不大于精軸1圈所代表的角度值的3/8時，所需邏輯判斷需處理3個重合位，它們是精軸讀數(14位)的最高3位(A、B、C位)和與之對應的粗軸讀數(10位)的第F、G、H位，判斷過程如下：

1)當ABC=000，FGH=111時，

K F G H

粗軸讀數：× × × × × × 111 ×

精軸讀： 000 × × × × × × × × × × ×

A B C

如果把粗軸1圈平均劃為8個區域，即M1～M8，把精軸1圈平均也劃為8個區域，即N1～N8，(見圖4)，則ABC=000表明精軸的轉角在N1區，FGH=111表明粗軸的轉角在M8區。與此相對應，粗軸的FGH=111表明從第F位開始到最末位數字所代表的角度小于精軸1圈的角度，但大于精軸1圈的7/8，即相當于處在精軸的N8區域。這就產生了一個問題，既然精軸位于N1，則表明它剛剛轉完1整圈。如果粗、精通道同步的話，此時第K位應加上1。但是FGH=111，第F位還沒有向第K位進位，第K位上少計了1個1，這樣構成的組合讀數，因第K位少1，將產生5.625°的負誤差。為了糾正這一誤差，應在該位加上1個1。

圖4 粗軸、精軸組合關系圖

2)當ABC=111，FGH=000時，

K F G H

粗軸讀數：× × × × × × 000 ×

精軸讀數： 111 × × × × × × × × × × ×

A B C

由圖4可知，精軸此時位于N8區域，而粗軸已經進入M1區域，第K位肯定多計了1個1，為糾正這一誤差，應在該位減去1個1。

3)當ABC=011時，此時精軸位于N4，因假定粗通道誤差不大于精軸1圈的3/8，所以粗軸不可能位于M8，在第K位上不會產生多1或少1的現象，因而無模糊誤差[6]。同理可知，粗、精軸組合糾錯規律見表1。

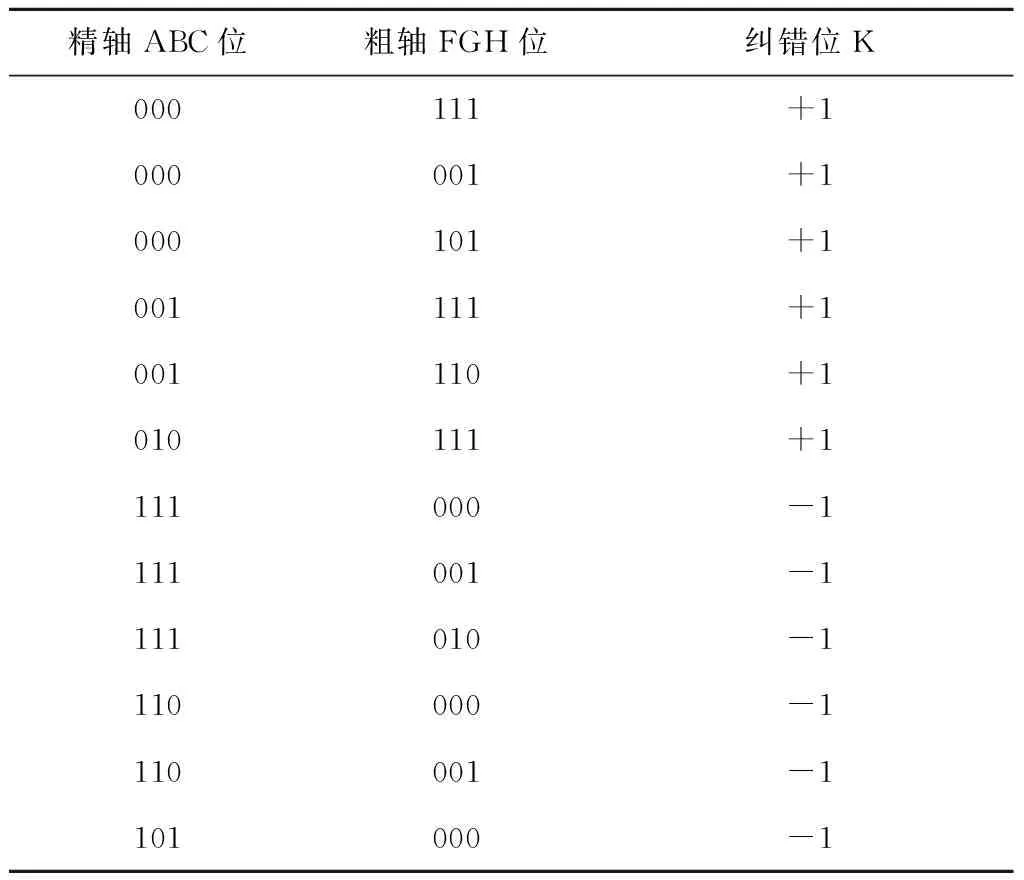
表1 粗軸、精軸組合糾錯碼

該部分軟件的實現首先分別取出粗軸、精軸的3位，生成2個二進制數M和N。根據表1建立一個3列、12行的十六制的數組，第1列是M的值，第2列是N值，第3列是相應的糾錯碼。當糾錯位需要加1時，糾錯碼是0010(十六進制)；當糾錯位需要減1時，糾錯碼是0010的補碼FFF0。查找數組，若在數組中找到對應的M、N，那么對粗軸進行糾錯計算，粗軸讀數=粗軸+糾錯碼；若查找不到，則不需要進行糾錯計算。糾錯后算出最后的結果2個16位的二進制數RH=粗軸/26(高4位)，RL=粗軸×210/214+精軸(低16位)。組合糾錯程序流程圖如圖5所示。

圖5 粗精組合糾錯程序流程圖

2.3 系統轉換精度

粗精轉換系統的分辨率取決于粗精傳動比和轉換器的分辨率，速比越高和轉換器的分辨率越高，整個系統的分辨率越高，很容易獲得所期望的分辨率。對14位轉換器，用于1∶64的精軸系統，得到的分辨率為：

360°/(26+220)=1.2″

粗精機電系統的傳輸精度可表示為：

(1)

式中，Bt為齒輪箱的齒隙；Ct為相對于粗軸嚙合的圓周誤差；St為精旋轉變壓器的精度。

對于數字粗精系統的傳輸精度需要把轉換器的精度加到等式中，這樣，整個系統的精度為：

(2)

式中，Dt為精轉換器的精度。

從式中的第3項(Dt+St)/n可以看出，系統精度與精旋轉變壓器的精度和精轉換器的精度有關。

在本系統中，精轉換器為14位，Dt=±4.5′；其他部分精度為：St= ±10″，Bt=±(1/2)′，Ct=±(1/4)′，n=64。因此，系統精度為：(1/2)′+(1/4)′+(4.5+1/6)′/64 = 0.82′。

2.4 誤差分析

系統采用粗精組合系統來提高測角精度，由于齒輪及傳動機構的間隙，測角元件及線路的精度等會造成誤差，使得粗精通道不能達到理想配合。誤差主要包括機械誤差和其他誤差。

2.4.1 機械誤差

在實際應用中，旋轉變壓器的軸通過齒輪直接與系統的輸入軸連接，齒輪的徑向跳動和偏心將不可避免地引起角誤差。主要機械誤差有徑向跳動誤差、旋轉變壓器軸偏心率誤差和安裝直徑誤差等。

2.4.2 其他誤差

其他誤差主要包括零位誤差、跟蹤誤差和器件誤差等。

1)零位誤差。旋轉變壓器的零位誤差是指當原邊激磁繞組加基準電壓激勵后，副邊輸出繞組輸出隨轉角θ呈正(余)弦函數變化的電壓，每一個電氣角度出現1個零點，該零點可能與理想零點偏離1個角度Δθ，這實際偏離的角度Δθ就是零位誤差。本系統零位誤差消除的方法是用軟件置零，在角度范圍內位置均可實現。

2)跟蹤誤差。任何伺服系統在跟蹤過程中都存在誤差。在求取該誤差時，首先確定系統的速度常數Kv，然后求出最大跟蹤速度時的跟蹤誤差，并和整個機構誤差作代數相加。

3)器件誤差。輸入、輸出器件會導致系統靜態不精確，如軸承的安裝和旋轉變壓器轉子的調整使系統產生誤差，一般情況下，器件誤差為常溫狀態下的誤差值，誤差隨溫度變化，可參考誤差隨溫度變化的曲線。轉換器件的轉換誤差和器件的精度有關。

2.4.3 消除誤差的方法

本系統采用粗精組合方法來消除各種誤差，在實際使用中，用軟件來合理組合粗、精軸的讀數值，采用余數比較法對數據進行糾錯，此方法可以有效減小誤差的影響。使系統滿足設計要求。

3 結語

本文采用了旋轉變壓器作為測角元件，選定旋轉變壓器數字轉換器作為數字轉換器件，采用單片機處理方式，用余數比較法對粗、精軸讀數進行組合糾錯，組成粗精組合角度測量系統，主要研究結論歸納如下。

1)采用粗精組合方式對粗軸讀數和精軸讀數進行粗精組合，提高了傳感器的測角精度，采用本文測角系統，精度可以達到0.82′，有效地提高了傳感器的輸出精度。

2)該系統在使用過程中，不需要調整旋轉變壓器的零位，用軟件可以設置零位，減少了零位調試的過程，使用方便。

3)用軟件實現多極旋轉變壓器粗精機組合的傳動比是1∶64。當傳動比為其他值時，如1∶36或1∶128，只需更換相應部分的具體值即可，因此該方法具有普遍意義。用軟件實現粗、精機軸角組合的方法較之硬件實現的組合方法更為經濟實用。

[1] 馬克剛. 同步器解算器及其工程系統設計實踐[M]. 北京：兵器工業出版社，1996.

[2] 詹訓慧，陳寶國. 雙通道多級旋轉變壓器的角度組合算法研究[J]. 微電機，2012(12): 55-58.

[3] 侯孝民，王元欽，張若禹. 精粗組合型軸角數字轉換器設計[J]. 指揮技術學院學報，1998(3): 81-85.

[4] 劉升才，王茂，曾慶雙. 雙通道測角系統中的粗精耦合問題[J]. 黑龍江自動化技術與應用，1994(2): 105-108.

[5] 金艷艷. 模塊化軸角/數字轉換器的選用及系統設計中的有關問題[J]. 雷達與對抗，1998(4): 15-18, 59.

[6] 謝顯之，劉新躍，于永昌. 軸角編碼粗精組合糾錯算法的研究與實現[J]. 計量與測試技術，2001(3): 6-7, 9.