初中數學測評題的編寫研究
袁婷婷
(太原市第52中學)
一、重視基礎知識,重視能力形成的過程
《義務教育數學課程標準》強調:數學教學必須建立在學生的認知發展水平和已有的知識經驗基礎之上。例如:
畫出在數軸上距離原點2個單位長度的點,它表示的數是_______,也就是說絕對值等于2的數是_______。
本題設計將學生的動手操作,用數軸上的點表示數,絕對值的定義融于解決問題的思維過程中,充分體現了初中數學命題要重視基礎知識和重視能力形成的過程。
二、適度回歸生活生產實踐
課程標準倡導學生的學習應該從生活出發,從周圍事物的具體形象中感知,使學生真正認識數學知識,學習數學知識,使學生的思維能力得到發展。因此,數學測評題要與生活緊密聯系,體現數學來源于生活又應用于生活的特點,引導學生把數學課堂中所學的知識和方法應用于生活實際之中。例如:
某文藝團體為“希望工程”募捐義演,成人票8元,學生票5元。(1)成人票賣出600張,學生票賣出300張,共得票款多少元?(2)成人票款共得6400元,學生票款共得2500元,成人票和學生票共賣出多少張?
(3)如果本次義演共售出1000張票,籌得票款6950元,成人票與學生票各售出多少張?
這樣的試題可以使學生知道數學知識來源于生活,也應用于生活。正是因為真實的生活情境引發了學生主動探索的熱情,學生自然而然把日常生活積累的經驗用到解決數學問題中來。真正體驗了對數學知識的理解和解決問題的成就感,同時也消除了對測評的畏懼心理。
三、突出問題意識,關注思維形成和動手實踐
陶行知先生說:“行動生困難,困難生疑問,疑問生假設,假設生試驗,試驗生結論,結論生行動。”測評試題中,設置新問題,學生動手實踐,主動解決問題的過程就是創新的過程。在測評試題中突出問題意識,一是可激發學生學習欲望,二是可優化教師的教學行為。
《義務教育數學課程標準》指出:教師應激發學生的學習積極性,向學生提供充分從事數學活動的機會。編制測評中,教師要結合具體的教學內容,為學生創設一個實踐操作的情境,讓學生動手實踐操作,使之在探索中對未知世界有所發現,找到規律,并能運用規律去解決新問題。例如:
利用對稱性可設計出美麗的圖案。在邊長為1的方格紙中,有如圖所示的四邊形(頂點都在格點上)。
(1)先作出該四邊形關于直線l成軸對稱的圖形,再作出你所作的圖形連同原四邊形繞0點按順時針方向旋轉90°后的圖形。
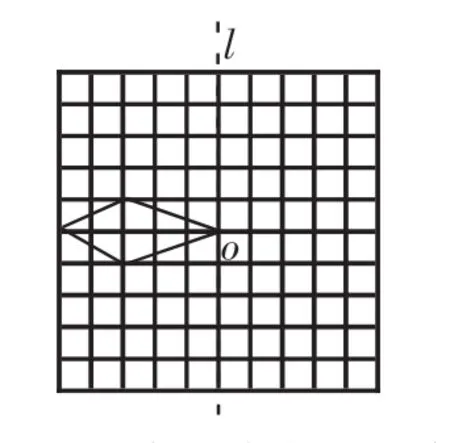
(2)完成上述設計后,整個圖案的面積等于_________。
這道題融學生問題意識、思維形成、動手操作于一體是現實的、富有挑戰的試題。數學是思維的體操,思維則是從動手實踐開始的,切斷了動手和思維的聯系,問題就得不到解決,思維也得不到發展。基于以上思考,命題突出問題意識,關注思維形成和動手實踐,使學生各方面能力都能得到進一步發展。
四、適度倡導開放
數學開放題,通俗地說就是給學生以較大認知空間的題目。素質教育的核心是培養創新精神和創造能力,數學開放題滿足了不同層次學生學習的需要。
1.問題的條件常常是不完備的。(條件開放題)
這類型目是給定結論來反探滿足結論的條件,而滿足結論的條件并不唯一,這類題常以基本知識為背景加以設計而成,主要考查學生對基礎知識的掌握程度和歸納能力。
例如:如圖,△ABC中,已知AB=AC,要使AD=AE,需要添加的一個條件是_____。
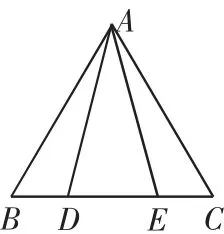
2.問題的解決策略具有非常規性、發散性和創新性。(策略開放題)
例如:試比較下面兩個幾何圖形的異同,如圖,請分別寫出它們的兩個相同點和兩個不同點。

正方形
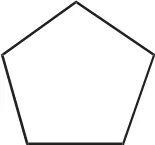
正五邊形
相同點:正方形的對角線相等,正五邊形的對角線也相等。
不同點:正方形是中心對稱圖形,正五邊形不是中心對稱圖形。
此題是考查學生正多邊形的知識和有關性質,通過觀察分析能從正多邊形的邊、角(中心角、內角和)對稱性有無外接圓與內切圓,從一個頂點作三角形的個數等方面去理解,就可以寫出很多相同點與不同點。
總之,數學測試題的編制是數學教師的一項專業化工作,懂得測試題的編制是數學教師應有的一項教學基本功。做好測試題的編制有利于了解學生的學習情況,正確評價學生的數學學習,激勵學生的學習和改進教師的教學。

