基于模糊C-均值和特征加權法的協同過濾推薦算法*

字云飛，李業麗，孫華艷，韓 旭

(北京印刷學院 信息工程學院，北京 102600)

0 引言

在當今大數據、人工智能(AI)時代，自媒體數據、出版數據、社交網絡數據、電商數據等成為人們現實與虛擬生活的重要組成部分。為解決大數據時代的海量數據和用戶隱性需求之間的矛盾，衍生了精準化和個性化推薦系統，且廣泛應用于電商行業。個性化推薦系統為用戶獲取隱性需求節約了時間、空間等成本，也是解決信息過載的最佳途徑。隨著網購便捷度不斷改善，用戶對于網購依賴性極大增強，這也帶來了用戶隱性需求未能得到滿足的問題，促使個性化、精準化推薦系統在電商行業顯得前所未有的重要。傳統協同過濾算法在電商、社交網絡個性化推薦領域得到了較為成功的應用，但隨著互聯網數據呈幾何級數增長、數據內容復雜度不斷提高等問題的凸現，這些已有算法也暴露了自身的局限性，協同過濾推薦算法[1-3]的缺點有：(1) 數據的稀疏性問題；(2) 新物品問題；(3) 可擴展性問題。

現有協同過濾推薦算法[4-7]主要通過用戶的歷史行為、興趣愛好等來實現個性化推薦，如根據用戶A和B相似度高，A對項目i感興趣，可以推測B也有可能對項目i感興趣，但推薦過程中如何應用高效的方法精準劃分項目候選集S成為推薦系統的核心，且候選集中每個子集i本身就是由多個模糊特征因素(x1,x2,…,xn)構成的，且多個特征因素集在項目中的權重又存在著差異，這會極大地影響推薦的精度和個性化。

很多學者基于協同過濾推薦算法[8-10]的不足，對其進行了不同維度的改進，但都沒有得到徹底解決。為了解決傳統推薦算法對用戶-項目精準化、個性化推薦過程中存在項目評分信息不足、特征值模糊性及權重偏向導問題，本文提出了一種模糊C-均值和特征加權法的協同過濾推薦算法。通過用戶在系統中的結構化、半結構化及非結構化數據記錄，通過奇異值分解法把用戶評分項分解為多個不同特征值來判斷用戶對未評項的喜好程度，然后再對C-均值計算出的候選集構建用戶-項目特征因素加權模型，計算用戶-項目核心特征因素的權值高低及價值大小，同時結合基于用戶-項目協同過濾推薦算法的相似度等數據信息尋找最近鄰，最后對用戶-項目進行綜合預判及終值優化，從而實現對用戶顯性、隱性需求的高效性、精準化、個性化的推薦。實驗分析表明，該算法對于最近鄰推薦的準確性有了極大的提高，同時，明顯提升了個性化推薦系統精度，優化了推薦質量。

1 傳統的協同過濾推薦算法

傳統協同過濾(Collaborative Filtering，CF)推薦算法是根據用戶-項目之間的評分、收藏、瀏覽信息等數據分析、計算相似度，從而尋找最近鄰，最后實現對目標用戶-項目的精準、個性化推薦。協同過濾推薦算法[11-15]分為基于用戶的協同過濾推薦算法和基于項目的協同過濾推薦算法。

1.1 協同過濾推薦算法的實現

(1)用戶-項目數據的收集及預處理。

(2)基于清洗后的數據來計算用戶-項目的相似度，選取最近鄰或相似度最高的N個用戶或項目。

(3)把N個相似度最高的用戶或項目推薦給對應的項目或用戶。

1.2 相關度評價計算

協同過濾推薦系統中，D=(U,I,R)用來表示用戶-項 目的數據源。U=(User1,User2,…,Usern)為用戶集，|U|=n；I=(Item1,Item2,…,Itemm)為項目集，|I|=m。用戶對項目的評分矩陣為Rm×n，其中Rij表示用戶Useri對項目Itemj的評分，表1為評分矩陣R。

協同過濾推薦算法中計算機相似度的常用方法為Pearson相關系數法，通過用戶對產品的評價數據計

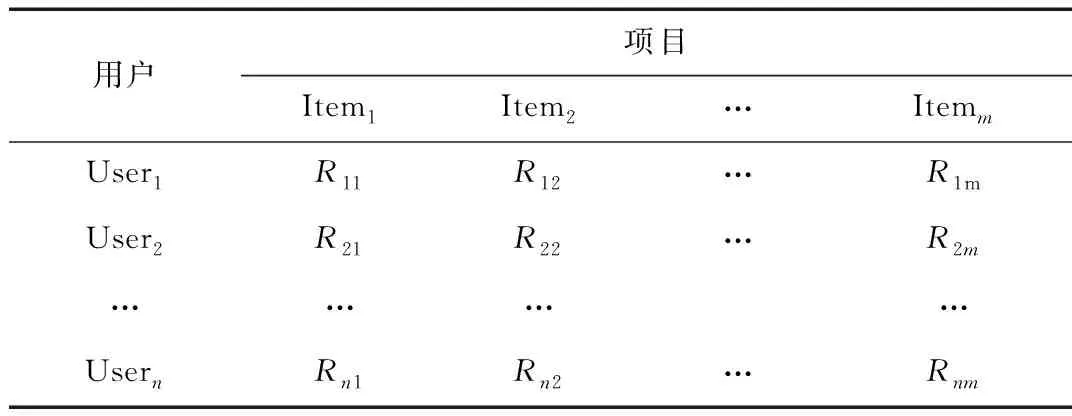
表1 用戶-項目評分矩陣

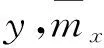
(1)

計算相似度之后尋找最近鄰，Zum為最近鄰，對項目s預測評分的計算如下：

(2)

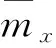
(3)

其中：Ts是項目總和，muw表示u對產品w的評價值。

2 模糊C-均值的候選集篩選

模糊C-均值聚類[16-17](Fuzzy C-Means clustering，FCM)算法是把項目集轉化為模糊等價關系，通過最佳閾值法來劃分項目集，劃分為N個相似度較高的類。其過程為：根據選取的N個樣本分為C類，而任何一個類都有自己的一個聚類中心，然后通過樣本與聚類中心的距離，計算得到特征值相同或相似的最近聚類中心模糊子集，最后獲得推薦項或用戶的最佳候選集。描述過程如下：

給定數據集X={x1,x2,…,xn}包括N個樣本，數據集可以劃分為c(1≤c≤n)類，則模糊目標函數定義為：

(4)

(dik)2=xk-vi=(xk-vi)TA(xk-vi)

(5)

其中：U=[uik]，uik∈[0,1]表示隸屬度矩陣；V=[vi]，i=1,2,…,c，vi為聚類中心矩陣集合，m=2為模糊指數；J(U,V)表示所選樣本與各聚類中心的距離總和；A要求對稱陣；dik是歐氏距離。

最小化聚類J(U,V)：min{J(U,V)}則：

(6)

當多次迭代之后，聚類中心向量和隸屬度矩陣為：

(7)

(8)

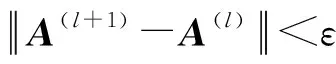
FCM算法實現過程：

Step1:確定類別劃分數C，模糊指數設置為2(m=2)，迭代停止參數ε；

Step2:對于聚類中心P初始化；

Step3:計算原數據的隸屬度矩陣U；

Step4:通過公式(7)更新聚類中心矩陣C；

Step5:通過矩陣C計算得到所需的用戶-項目之間的距離dik及隸屬度矩陣U*，如dik=0，則uik=1；

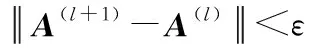
Step7:根據最后計算得到的隸屬度矩陣對用戶-項目數據進行模糊聚類獲得候選集。

3 對篩選候選集進行特征加權法

通過C-均值聚類之后得到的推薦候選集是一個屬性值相似度較高的類，但要對用戶-項目實現精準、個性化推薦仍存在著分類精度不高、個性化特征不足的缺陷。因為每一個推薦候選集的用戶-項目信息本身又有特征值權重比，而特征值加權更能夠客觀、精準的表達事物本身，所以通過對C-均值聚類之后的候選集進行特征加權法能夠更精準、個性化實現推薦結果。

在實際的推薦過程中，用戶和項目都是由多個特征屬性組成的，而特征屬性[18-19]沒有嚴格、準確的分界線，所有它們就構成了描述用戶-項目本身的模糊特征集，而每一個模糊特征集是由若干個特征值相互作用而成的，且每一個特征因素又可以用一個特征模糊集來表示，此時的用戶-項目論域可以表示為n個因素集的Descartes乘積，即

U=U1×U2×…×Un

設Ai∈Ui(i=1,2,…,n)，Ai為某一個用戶或項目特征因素集的子集，A∈U，A是由用戶-項目特征因素集A1,A2,…,An復合而成的。

3.1 加權平均法

給一個用戶推薦某一個項目是基于用戶本身的興趣愛好，而興趣喜好是由用戶的職業、性別、教育程度、生活環境等諸多因素決定和影響的，而每一個因素又由多個特征值構成，且每個特征因素決定項目或用戶本身的比重又存在著差異，所以賦予特征模糊集中的特征因素在用戶-項目中的權重比能夠使推薦系統更加精準、高效和個性化。

若用戶-項目A(u)是由n個子特征集A1(u1),A2(u2),…,An(un)累加而成的，則精準計算用戶-項目特征本身為：

(9)

3.2 乘積平均法

當推薦用戶或項目特征因素按比例變化時，如某一用戶感興趣的項目特征集A中有n個特征子集，其中每一個特征子集Ai是按比例變化的，可用乘積平均法計算機用戶-項目推薦候選項的精度。

若用戶-項目特征集A(u)是隨(Ai(ui))αi按比例變化的，且每個特征子集Ai(ui)對特征因素集合A(u)都是必要的，當任意一個Ai(ui)為零時，A(u)都為零，則乘積平均法計算特征因素公式為：

=b(A1(u1))α1…(An(un))αn

(10)

其中：u=(u1,u2,…,un)∈U為用戶-項目特征集，(α1,α2,…,αn)為特征因素在用戶-項目中的權重向量，b為適當選取的常數，以保證A(u)∈[0,1]。

3.3 混合法

如果決定用戶-項目特征因素集A(u)的子特征因素Ai(ui)可以分為兩部分，一部分用戶-項目的特征因素按權重比累加，另一部分做乘積，則計算用戶-項目特征因素為：

(11)

其中：特征因素集u∈U，(α1,α2,…,αm)，(δ1,δ2,…,δk)為兩權重向量，且m+k=n+1，b為正實數，權重(α1,α2,…,αm)、(δ1,δ2,…,δk)通過實驗取點。

3.4 特征因素加權綜合法的協同過濾算法

根據前文論述，算法1實現向目標用戶U1的精準、個性化推行過程。

算法1 基于特征因素加權綜合法

輸入：候選集信息D=(U,I,R)和權重向量

輸出：為用戶U1產生推薦集S

Begin：

(1)對用戶及項目的原始特征因素進行預處理；

(2)選取用戶U1訪問記錄的N個項目的特征因素值；

(3)Repeat

(4)Fori=1:n{

(5)對選取的特征因素值進行加權平均及乘積平均計算獲得第i個特征值的重要程度(公式(9)、(10))；

(6)取出每個項目特征因素最重要的前n個值，然后通過綜合加權計算推薦項目A；

(7)}

(8)產生推薦集S；

End

基于因素加權綜合法的協同過濾推薦算法通過對用戶-項目特征因素值的加權研究，計算特征因素值對于用戶-項目的重要程度來產生對目標用戶或項目的推薦候選集，從而實現精準、個性化的推薦。

3.5 算法復雜度分析

算法復雜度包括時間和空間復雜度，它是有效衡量算法執行效率的指標。

計算目標用戶-項目與篩選K個相似度較高的推薦項的過程是傳統協同過濾推薦算法計算時間復雜度的核心，通過對推薦集及目標用戶-項目之間相似度的計算，結合N個用戶-項目的準確評分項得到。因此，計算M個用戶-項目與目標用戶-項目之間的相似度的時間復雜度為O(N×M)，且N、M數量級一致，故時間復雜度為O(N2)。

基于C-均值和特征加權法的協同過濾推薦算法通過對目標用戶-項目篩選出候選集及對候選集用戶-項 目的特征值權重偏向計算其相似度得特征向量(V1,V2,…,Vs)，然后通過相關度評價法(Pearson)計算特征向量與目標類別矩陣之間的距離。而C-均值和特征加權法計算相似度的時間復雜度為O(S×N)，相關度評價距離時間復雜度為O(S×M)，因此時間復雜度總和為O(S×N)+O(S×M)。因N、M數量級一致，而特征因素值S相比于N、M極小，則時間復雜度為O(N)。

4 實驗仿真及分析

4.1 實驗環境

算法性能分析的實驗環境以Windows 7操作系統為實驗支撐，相關配置為Intel Dual Core 2.5 GB處理器，編程語言Python，8 GB內存，2.60 GHz雙核CPU，MySQL數據庫。

4.2 數據集合

為了比較基于C-均值和特征加權法的協同過濾推薦算法與傳統用戶-項目協同過濾推薦算法之間推薦精度、效率的差異，實驗數據基于University of Minnesota項目小組(GroupLens)提供并維護的MovieLens數據集(http://www.grouplens.org/)來進行真機實驗。數據包括945個用戶對于1 681部電影項目的100 000個評分數據信息，且一個用戶至少存有對25部電影的評分記錄，評分值為1～5，值越大用戶喜好度越高。同時，實驗數據按需求進行訓練集TrainSet與測驗集TestSet劃分，且二者沒有交集。

4.3 數據稀疏性

利用用戶對于電影的評分值表達對電影的喜愛程度。數據的稀疏性為：

1-100 000/(945×1 681)=0.937 049

表明數據的稀疏性非常高。

4.4 度量標準

本文應用的統計精度測量中的絕對誤差法(MAE)是度量推薦結果好壞的最有效方法之一。MAE值越小表明推薦精準度及效果越高。

(12)

其中：|itemtestset|表示項目集中評分項的個數，predi{pred1,pred2,…,predN}為對于算法預估的評判分數，qi{q1,q2,…,qN}為測試數據的實際分數。

4.5 實驗結果

實驗基于MovieLens數據集對傳統的協同過濾推薦算法與基于C-均值和特征加權法的協同過濾推薦算法進行了平均絕對誤差值的比較分析，如圖1所示。最近鄰的數量也將影響推薦的效果，過少將會降低推薦的精準性，過多將極大增加算法復雜度，實驗中選取最近鄰的數量為10～40。

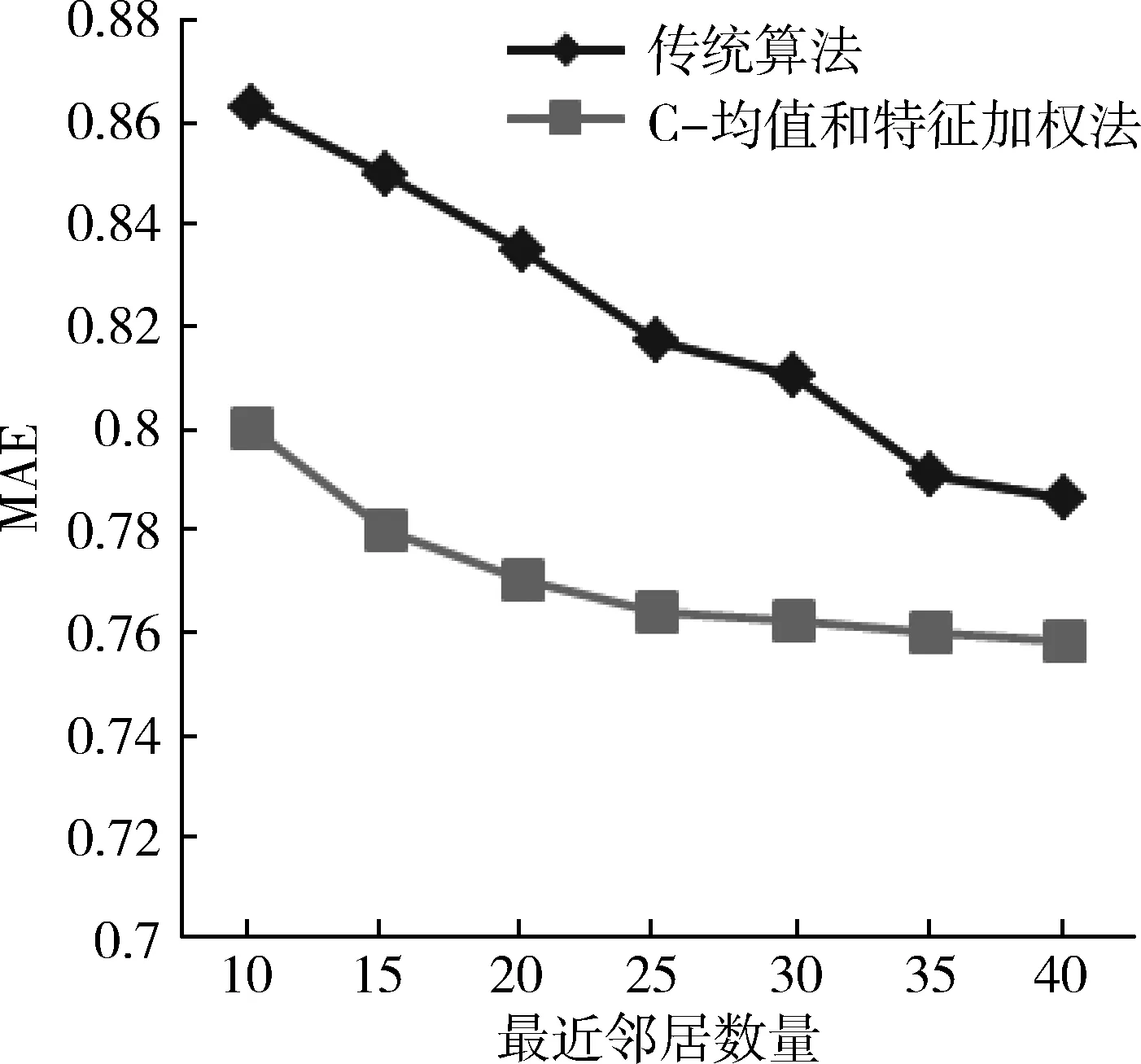
圖1 兩種算法的MAE比較

通過圖1可知，隨著最近鄰居數量的增大，無論是傳統過濾推薦算法，還是基于C-均值和特征加權法的協同過濾推薦算法，平均絕對誤差值(MAE)都呈下降趨勢，但不管近鄰數值多少，只要最近鄰數相同，基于C-均值和特征加權法的協同過濾推薦算法的平均絕對誤差值(MAE)都低于傳統推薦算法，由此表明本文的推薦算法具有較高的精準度。所以采用基于C-均值和特征加權法的協同過濾推薦算法對提高推薦系統的精準度及執行效率都有明顯的幫助。

5 結束語

本文提出的基于C-均值和特征加權法的協同過濾推薦算法首先對樣本數據進行C-均值聚類篩選候選集，再通過對用戶-項目特征因素值權重向量的劃分，計算每一特征因素值對于用戶-項目的重要程度，從而精準劃分候選集，提高相似度的度量。各推薦算法中相似度度量好壞將直接影響推薦項目或用戶的精準度和個性化。同時，該算法通過對項目或用戶特征值的內外距離計算或加權計算特征因素集，都能減小稀疏性帶來的負面影響。如何通過矩陣結合時間序列、云模型等來擴展因素加權綜合法的推薦算法以及應用于相關領域，是下一步研究的方向。

[1] Huang Hao, Huang Jianqing, ZIAVRAS S G, et al. A personalized recommendation algorithm based on Hadoop[C]//2015 5th International Conference on Electronics Information and Emergency Communication (ICEIEC).IEEE,2015:406-409.

[2] 秦光潔，張穎.基于綜合興趣度的協同過濾推薦算法[J].計算機工程，2009,35(17):81-83.

[3] 韋素云，業寧.基于項目類別和興趣度的協同過濾推薦算法[J].南京大學學報(自然科學)，2013,49(2):142-149.

[4] ADOMAVICUS G, TUZHILIN A. Toward the next generation of recommender systems: a survey of the state-of-the-art and possible extensions[J]. IEEE Transactions on Knowledge and Data Engineering, 2005, 17(6): 734-749.

[5] PARK C, KIM D, OH J, et al. Improving top-K recommendation with truster and trustee relationship in user trust network[J]. Information Sciences, 2016, 374:100-114.

[6] PAN J C, ZHANG X M, WANG X. Improved singular value decomposition recommender algorithm based on user reliability [J]. Journal of Chinese Computer System, 2016,37(10): 2171-2176.

[7] 孫光福，吳樂，劉淇,等.基于時序行為的協同過濾推薦算法[J].軟件學報，2013(11)：2721-2733.

[8] 王偉，王洪偉，孟園.協同過濾推薦算法研究:考慮在線評論情感傾向[J].系統工程理論與實踐，2014，34(12)：3238-3249.

[9] PERA M S, NG Y K. Analyzing book-related features to recommend books for emergent readers[C]// Proceedings of the 26th ACM Conference on Hypertext &Social Media. ACM, 2015: 221-230.

[10] 榮輝桂，火生旭，胡春華.基于用戶相似度的協同過濾推薦算法[J].通信學報，2014(2):16-24.

[11] 李豪，張海英，張俊.一種基于用戶興趣分析的協同過濾推薦算法[J]. 微型機與應用，2017,36(15):25-28.

[12] Zhang Qinghua, Xu Kai, Wang Guoyin.Fuzzy equivalence relation and its multigranulation spaces[J]. Information Sciences,2016, 346-347(C)：44-57.

[13]Hu Liang, Wang Wenbo, Wang Feng, et al. The design and implementation of composite collaborative filtering algorithm for personalized recommendation[J]. Journal of Software, 2012: 2040-2045.

[14]Yang Hai. Improved collaborative filtering recommendation algorithm based on weighted association rules[J]. Applied Mechanics and Materials,2013:94-97.

[15] Liu Fengming, Li Haixia, Dong Peng. A Collaborative filtering recommendation algorithm combined with user and item[J]. Applied Mechanics and Materials,2014:1878-1881.

[16] Duan Lingzi,Yu Fusheng, Zhan Li.An improved fuzzy C-means clustering algorithm[C]//2016 12th International Conference on Natural Computation, 2016:861-865.

[17] ZARITA Z, ONG P. An effective fuzzy C-means algorithm based on symmetry similarity approach[J]. Applied Soft Computing Journal,2015, 35(C): 433-448.

[18] Luo Xin, Zhou Mengchu, Xia Yunni, et al. An efficient non-negative matrix-factorization-based approach to collaborative filtering for recommender systems[J]. IEEE Transactions on Industrial Informatics, 2014, 10(2): 1273-1284.

[19] PARK Y, PARK S, JUNG W, et al. Reversed CF: a fast collaborative filtering algorithm using a K-nearest neighbor graph[J]. Expert Systems with Applications, 2015, 42(8): 4022-4028.