基于Floyd改進加速算法的最短路徑選擇*

馬 瑩，陳志龍，劉 賀，趙銅星

(1.陸軍工程大學 國防工程學院，江蘇 南京 210007；2.海峽之聲廣播電臺，福建 福州 350000；3.解放軍理工大學 野戰工程學院，江蘇 南京 210007)

0 引言

最短路徑問題是求解復雜網絡關鍵節點的關鍵，是評價復雜網絡的一個重要特征，特別是大規模網絡的最短路徑問題一直是亟待解決的難題。如何對節點的重要性進行有效評估并發現與實際情況相符的關鍵節點成為當前研究的重點和熱點。張德全等人提出了不含負回路的網絡中 Floyd 加速算法及優化方法，并構造了求解最短路徑的序號矩陣[1]。王運明等人針對目前指揮控制網絡關鍵節點識別方法利用局部信息識別精度低、利用全局信息識別復雜度高的問題，提出了一種面向結構洞的指揮控制網絡關鍵節點識別方法[2]。嚴棟等人根據主觀與客觀賦權的特點，把熵權法的思想運用到AHP 算法，建立了新的復雜網絡關鍵節點識別方法[3]。左秀峰等人針對最短路問題中存在多條等價最短路徑的問題，基于Floyd設計出新的搜索算法，在迭代更新距離矩陣與路徑矩陣的基礎上求出所有等價最短路徑[4]。HU P從節點的初始重要性以及相鄰節點和非相鄰節點之間的相互依賴強度所做的重要貢獻兩個角度提出了一種新的節點重要性評價方法，并將其應用于電子郵件網絡[5]。周漩等人通過定義節點效率和節點重要度評價矩陣,提出了一種利用重要度評價矩陣來確定復雜網絡關鍵節點的方法[6]。曾瑛等人利用電網影響因子,并結合所定義的聚合系數指標,分析電力通信網中重要節點的分布密集狀況,得到各節點在網絡拓撲中的相對重要性[7]。張喜平等人引入m階鄰居節點的概念,提出了一種基于m階鄰居節點重要度貢獻的復雜網絡節點重要度方法,并引入α和γ兩個參數,用于調節節點重要度評估對節點自身特性及m階鄰居節點的依賴程度[8]。李鵬飛等針對傳統關鍵節點識別方法不能適應Ad hoc網絡拓撲動態性、計算復雜度高的問題,提出一種基于網絡連通性和節點刪除法相結合的關鍵節點識別方法[9]。

1 多層系統復雜網絡模型

就目前研究現狀來看，對多層系統復雜網絡的研究僅限于概念層面，在建模方式上采用單一類型的網絡，各子網要么均是隨機網絡，要么均是無標度網絡，沒有區分子網的不同類型，而在實際網絡中，尤其是多層系統網絡，由于其復雜性而不可能存在單一的網絡連接方式。

針對這一問題，基于多層現實系統本體，區分出不同類型的網絡節點形式，并由核心層節點出發按各類網絡形式進行輻射式構建。在各子網間采用確定性連接與隨機性連接共存的混合連接方式構建多層復雜系統網絡。

在確定性連接中存在“擇優”與“扶貧”兩種連接方式，新的節點可能加到核心節點比較強的節點之下，使“強者更強”；也可能補充到功能較弱或者已經被嚴重削弱的節點之下，彌補某個功能的不足。

在隨機性連接中又存在ER隨機網絡連接[10]和BA無標度網絡連接兩種方式[11]，連接方法如下。

(1)ER隨機網絡連接：每次都從N1個核心網絡節點中隨機選擇一個節點與新加入的子網節點連接，直到所有的隨機連接節點全部連接到網絡中。

(2)BA無標度網絡連接：新加入的節點與一個已經存在的核心網絡節點i以概率Pi連接:

(1)

從而，本文定義了反映網絡形式的三個比率：

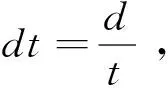
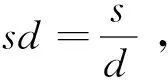
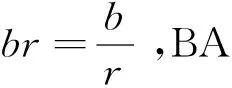
其中t為總連接數；d為確定性連接數；r為隨機性連接數；s為確定性擇優連接數；h為確定性扶貧連接數；b為BA無標度網絡連接數；e為ER隨機網絡連接數；它們存在的關系為：t=d+r，d=s+h，r=b+e。

當dt=br=0,sd無限制時，退化為ER隨機網絡連接；

當dt=0,br=1,sd無限制時，退化為BA無標度網絡連接；

當dr=1,sd=1,br無限制時，為完全確定性擇優連接；

當dr=1,sd=0,br無限制時，為完全確定性扶貧連接。

用這三個比率可以靈活控制網絡的連接規律，從而生成不同的網絡模型。因此，混合連接多層網絡模型構建方法如下：

步驟1 核心層節點標號, 確定3個混合比率(dtf,sdf,brf)；

步驟2 對每個新加入子網，生成m以內的隨機數，代表該點的連邊數；

步驟3 生成d=Nn×dt個節點進行確定性連接；

步驟4 按照核心節點的度值大小從大到小排序，將s=d×sd個新子網節點連接到前s個核心節點，將h=d×(1-sd)個新子網節點連接到后h個核心節點；

步驟5 生成r=Nn×(1-dt)個節點進行隨機性連接；

步驟6 將b=r×brf個節點按照BA無標度網絡規則連接到核心節點上；將g=r×(1-brf)個節點按照ER隨機網絡規則連接到核心節點上；

步驟7 新子網節點按概率Sh進行ER隨機連接。

基于Netlogo仿真平臺構建出的多層系統網絡模型有15個參數，具有很強的適用性，不同參數靈活組合可有成千上萬種變化，可以生成各種類型的目標體系網絡模型。由于系統網絡模型的建模過程是基于核心層級輻射式建立的，因此該模型不僅能夠研究整個系統網絡的特征，也可以單獨研究其中某個子網絡的特征。

2 最短路徑算法研究

傳統的求解最短路徑的算法主要有Dijkstra算法和Floyd算法，其中Dijkstra算法是計算網絡中一個節點到其他所有節點的最短路徑的高效算法，而Floyd算法是計算網絡中所有節點之間最短路徑的經典算法。

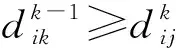
因此，本文針對無向無權的復雜網絡，從這三點出發進行優化，提出了改進的級聯失效算法，從而極大地提高計算效率。算法的優化思路如下：

(1)無向無權網絡的距離矩陣D為對稱矩陣，所以有dij=dji，求得dij后直接賦值給dji即可，不需要再計算dji，即在算法的最內層循環中，j不需要從1開始計算，而是從i+1開始計算，這樣j的平均計算次數減少為(n-1)/2，而且剔除了i=j的情況。

(2)當k=i或k=j時，節點通過自身到達另一節點，長度沒有變化，不需要計算，i和j直接遞增。

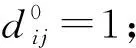
(4)因為網絡直徑R在運算結束前為未知數，所以設定一個變量C來表示還未找到最短路徑的節點對數量，當dij改變時，變量C減2，當C=0時，所有節點之間的最短路徑已經找到，算法終止。

因此，假定網絡中的節點數為n，關鍵節點評價算法的實現步驟如下：

令C為不相鄰的節點對總數。

步驟3：若C=0，則迭代結束；否則r=r+1，返回步驟2。

3 算法復雜性分析

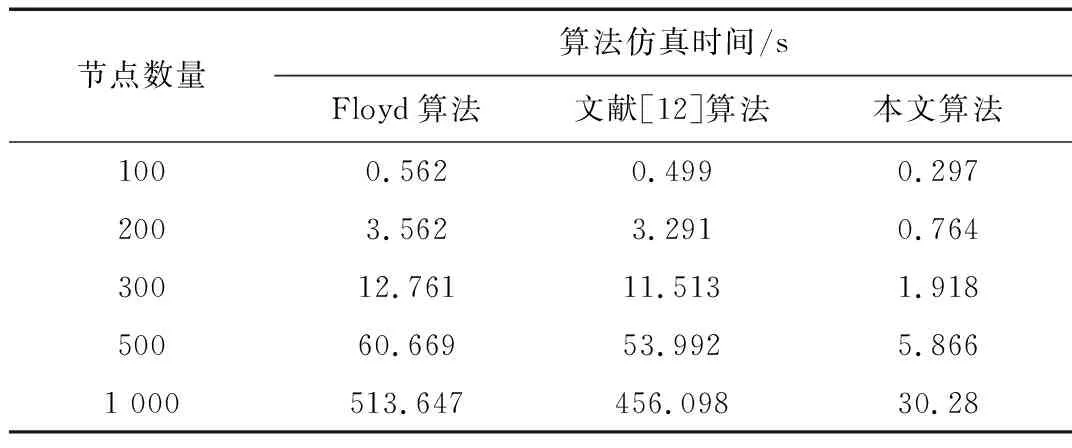
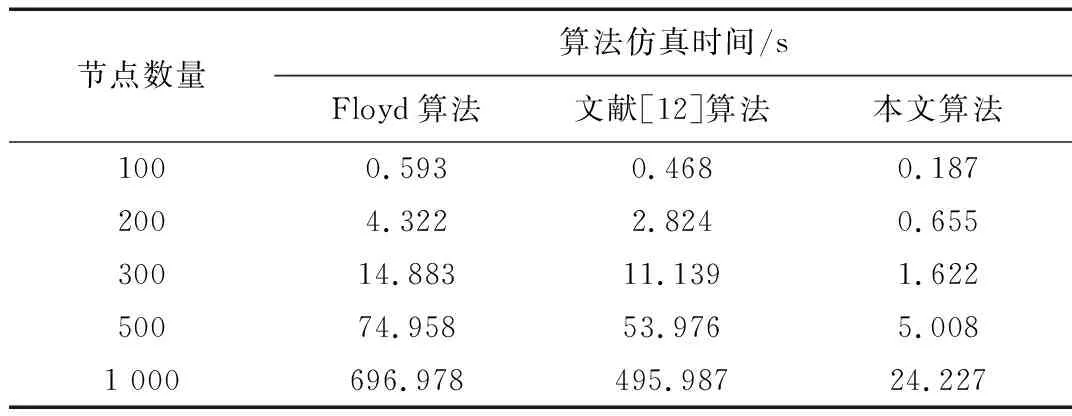
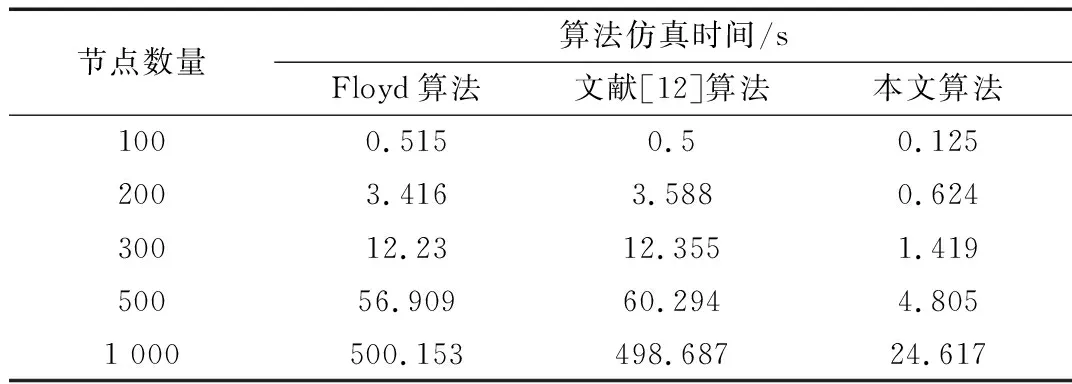
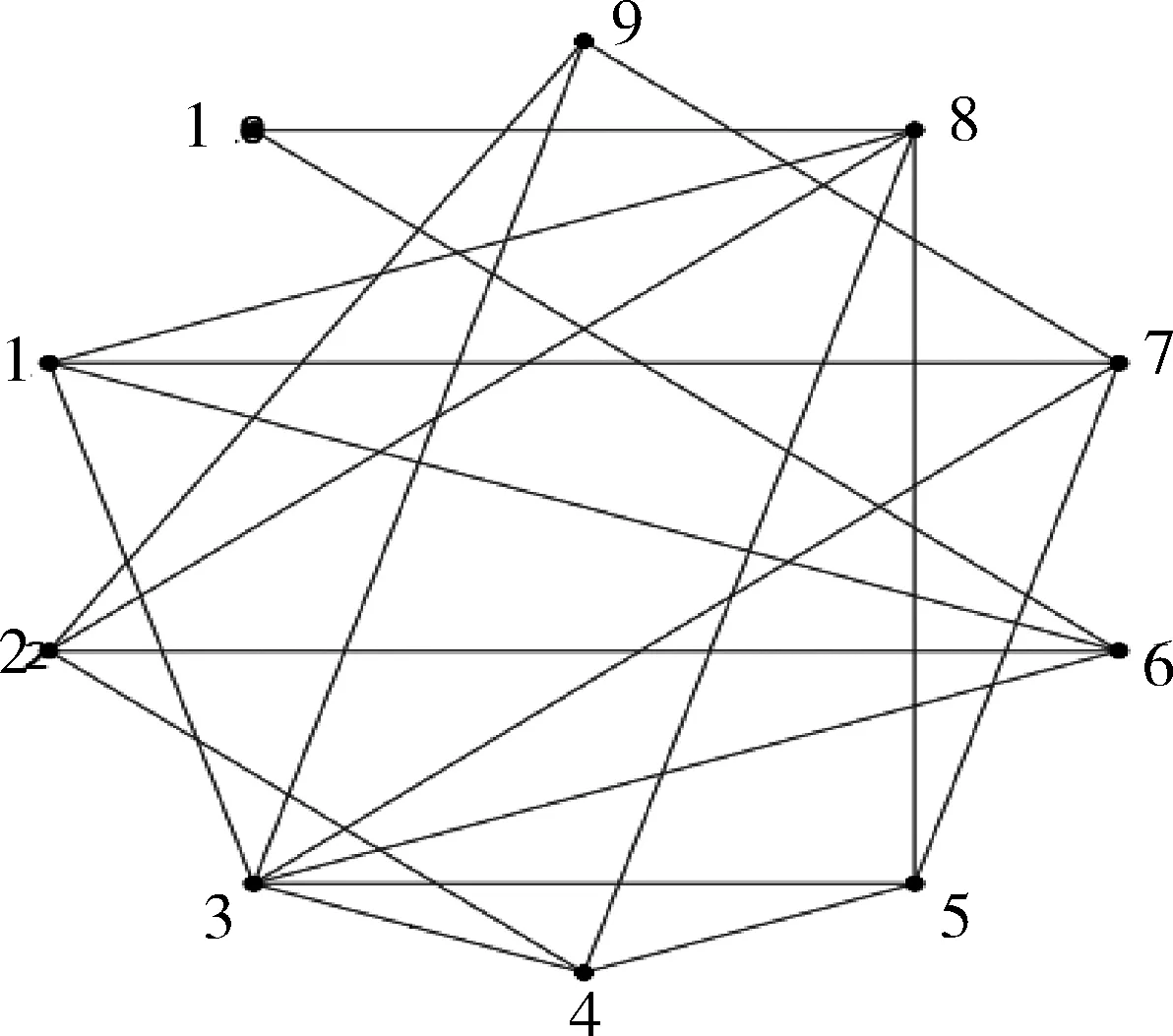
改進的Floyd加速算法共有四層循環，其中最外層r的循環次數為R-1，第二層k的循環次數為n，第三層i的平均循環次數為2L/n，其中L為邊數，第四層j的平均循環次數為(n-1)/2，算法總的復雜度為O((R-1)n(2L/n)(n-1)/2)=O((R-1)L(n-1))≈O(RLn)。通過分析可以看出，改進的Floyd加速算法的計算復雜度與網絡直徑R和邊數L有關，當R<

當網絡的節點數n固定時，要使網絡連通，邊數L至少為n-1，此時網絡的直徑R=n-1， Floyd加速算法的計算復雜度為O((n-1)(n-1)n)≈O(n3)；當網絡為完全連接網絡時L=n(n-1)/2，網絡直徑R=1，此時的計算復雜度為O(n2(n-1)/2)≈O(n3/2)。而該算法的最優計算復雜度約為O(n2)，所以隨著網絡連接邊數的增加，該算法的計算復雜度先減小后增大。

4 算法優越性驗證

在Netlogo中生成節點數為10的某地域通信網干線節點拓撲結構網絡模型如圖1所示，下面計算所有節點間的最短路徑長度。

圖1 某地域通信網干線節點拓撲結構網絡圖

解：由圖1得到初始距離矩陣：

不相鄰的節點對數C=50

當r=1，k=1時：

i=3，j=6，d36=1<2不變，j=7，d37=1<2不變，j=8，d38=>2，d38=d83=2；i=6，j=7，d67=>2，d67=d76=2，j=8，d68=>2，d68=d86=2；i=7，j=8，d78=>2，d78=d87=2；

當r=1，k=2時：

i=4，j=6，d46=>2 ，d46=d64=2，j=8，d48=1<2不變，j=9，d49=>2，d49=d94=2；i=6，j=8，d68=2不變，j=9，d69=>2，d69=d96=2；i=8，j=9，d89=>2，d89=d98=2；

當r=1，k=3時：

i=1，j=4，d14=>2 ，d14=d41=2，j=5，d15=>2，d14=d41=2，j=6，d16=1<2不變，j=7，d17=1<2不變，j=9，d19=>2，d19=d91=2；i=4，j=6，d46=2不變，j=7，d47=>2，d47=d74=2，j=9，d49=>2，d49=d94=2；i=5，j=6，d56=>2，d56=d65=2，j=7，d57=1<2不變，j=9，d59=>2，d59=d95=2；i=6，j=9，d69=>2，d69=d96=2；i=7，j=9，d79=1<2不變； ……

得到r=1時的距離矩陣：

當r=2，k=1時：

i=3，j=4，d34=1<3不變，j=5，d35=1<3不變，j=9，d39=1<3不變，j=10，d3,10=2<3不變；i=6，j=9，d69=2<3不變，j=10，d6,10=1<3不變；i=7，j=9，d19=1<3不變，j=10，d7,10=>3，d7,10=d10,7=3；……

得到r=2時的距離矩陣:

此時，所有節點對之間的最短距離都已經找到，該網絡直徑為3，邊數為20，總的計算次數T=(3-1)×20×(10-1)=360，而經典Floyd算法的計算次數為1 000，可以看出本文算法極大地降低了計算量。

文獻[12]中的Floyd加速算法的改進方法是目前最新、適用性較廣且獲得結果較好的一種計算節點間最短路徑長度的方法，為驗證本文算法的優越性，分別用Floyd算法、文獻[12]改進方法及本文算法求解隨機網絡、小世界網絡和無標度網絡的平均最短路徑長度來進行對比驗證，結果如表1～3所示。通過比較可以看出，針對最常用的三種網絡拓撲結構模型，本文提出的改進算法在計算節點間的最短路徑長度時，其計算復雜度較之經典的Floyd算法和文獻[12]提出的改進算法有明顯的降低，而且節點數量最大，優勢越明顯。將本文提出的改進的Floyd加速算法應用到實際系統網絡評價之中，將會極大地提高算法的計算效率，從而提高算法的應用價值。

5 結論

復雜網絡作為很多真實網絡的抽象，為描述和解決實際問題提供了一種途徑。針對多層系統網絡的研究，本文提出了一種新的輻射式建模方法并用新的改進的Floyd加速算法評價了網絡節點的重要性。本文所做的工作有以下幾點：首先，分析不同類型的節點連接方式，提出了混合類型連接方法。其次，以核心網為基礎，輻射式逐層生成系統網絡模型，提出了一種新的建模方式。最后，使用新提出的改進的Floyd加速算法評價了網絡中節點的重要性。通過仿真結果與已有研究結果進行對比，該方法不僅有很好的可靠性，還使得仿真時間縮短，達到了較好的仿真效果。 本文算法為多層網絡系統模型的建立和評估提出了一種新的思路，有著很好的理論價值和現實意義。

表1 隨機網絡模型三種算法復雜度對比

表2 小世界網絡模型(重連概率0.2)三種算法復雜度對比

表5 無標度網絡模型三種算法復雜度對比

[1] 張德全,吳果林,劉登峰.最短路問題Floyd加速算法與優化[J].計算機工程與應用,2009,45(17):41-44.

[2] 王運明,王青野,潘成勝,等.面向結構洞的指揮控制網絡關鍵節點識別方法[J].火力與指揮控制,2017,42(3):59-63.

[3] 嚴棟,張世斌,宗康,等.基于AHP-熵權法的復雜網絡關鍵節點識別方法[J].廣西大學學報,2016,41(6):1933-1939.

[4] 左秀峰,沈萬杰.基于Floyd算法的多重最短路問題的改進算法[J].計算機科學,2017,44(5):232-234,267.

[5] HU P, FAN W, MEI S. Identifying node importance in complex networks[J]. Physica A: Statistical Mechanics and its Applications, 2015, 429: 169-176.

[6] 周漩,張鳳鳴,李克武,等. 利用重要度評價矩陣確定復雜網絡關鍵節點[J].物理學報，2012,61(5):1-7.

[7] 曾瑛,朱文紅,鄧博仁,等. 基于電網影響因子的電力通信網關鍵節點識別[J]. 電力系統保護與控制,2016,44(2):102-108.

[8] 張喜平,李永樹,劉剛,等. 節點重要度貢獻的復雜網絡節點重要度評估方法[J]. 復雜系統與復雜性科學,2014,11(3):26-32

[9] 李鵬飛,雷迎科. 動態Ad hoc網絡關鍵節點識別[J].計算機應用研究，2017,34(5)：1473-1475.

[10] INSOO S. Small-world and scale-free network models for IoT systems[J]. Mobile Information Systems, 2017(61): 1-9.

[12] 左秀峰,沈萬杰.基于Floyd算法的多重最短路問題的改進算法[J].計算機科學,2017,44(5):232-234,267.