新課改下初中數學教學的幾點思考
◆
(吉林省鎮賚縣四方坨子學校)
一、塑造問題場景激發學習興趣
初中數學教師依托教學內容,結合學生好奇心,通過問題塑造場景,達成激發學生學習興趣與動力的目的。
如“正多邊形與圓”學習時,教師可以塑造以下問題場景:直接展示我國古代園林的藝術風貌,將自然美體現出現,最后將畫面固定在一個八角亭上,進而引發出問題:中國古代園林藝術風貌多采用正多邊形的亭子,你們知道古人怎們畫出正多邊形呢?你自己可以畫出正多邊形嗎?
隨著這一問題的提出,可以有效激發學生學習興趣,激發思維,為后續學習夯實基礎。
二、引入生活實例活躍課堂氛圍
數學概念具有抽象性、復雜性的特點,這些概念直接理解難度較大,需要教師創新教學方法。大部分抽象改變都是基于生活感性認識產生的,因此概念教學中可以引入生活實例,通過大量生活實例幫助學生認識與掌握概念,最終達成熟練運用的目的。
如“梯形”概念講解時,可以將生活中梯子、堤壩橫截面等生活中常見的例子展開出來,讓學生對梯形有一個直觀的認識,主動總結梯形特征,進而延伸出初步梯形概念。再如,“數軸”概念,直接將生活中用于稱東西的桿秤拿到課堂上,讓學生仔細觀察桿秤上有什么東西,整個過程中教師不斷引導,最終總結桿秤上存在三個要素,即度量起點、度量單位及增減方向。通過啟發、引導總結出數軸改變的三要素。通過借助學生熟悉的生活實例教學,可以將抽象的概念具體化,還可以培養學生實踐能力。
三、有效培養與鍛煉思維的能力
初中數學教師靈活運用基礎知識激發學生學習靈感,通過設計一些開放性題目掌握知識點。促使學生以基本數學思想為出發點,經過觀察與思考通過構建數學模型解決實際數學問題,這是培養初中生創造性思維的主要渠道,達成提高初中生數學素養的目的。
例如,已知(z-x)2-4(x-y)(y-z)=0,求證:x、y、z三者呈等差數列。
解析:學生初看題目,會覺得一頭霧水,找不到解題的出發點。如果選擇去括號整理題目,整個解題過程將變得異常繁瑣。教師可以引導學生仔細觀察,給出解法。
設a=x-y、b=y-z,推出z-x=-(a+b)
∴(z-x)2-4(x-y)(y-z)=0變為(a+b)2-4ab=0
∴x-y=y-z
∴x、y、z三者呈等差數列
這個題目本來難度較大,通過合理構建后難度大幅度降低。教師可以通過這種方法培養學生思維靈感,創造出更多簡便的計算方法,實現培養創新思維與能力的目的。
四、創新教學方法提高教學質量
初中數學教學是確保高中數學教學能夠順利開展和進行的基礎和前提,所以教師在進行初中數學教學時,一般都會先教會學生對量角器、直尺、三角板等輔助作圖工具的使用,幫助學生在后期學習時能夠自行繪制函數圖像,能夠在以后處理幾何解題法時自行進行圖像轉化。而且,很多初中生都能夠順利掌握這種基本的圖形知識,這對于數形結合思想在初中數學教學中的開展十分有利。
如李明和韓梅梅是同桌,在這周五放學時他兩約好第二天早上一起到距家900M的公園去劃船,第二天李雷和韓梅梅從家到公園的時間都為20min,但到公園后,李雷因為提不起興趣提前回家,回家消耗的時間同樣為20min,而韓梅梅在公園劃了10min船才回家,回家花費了15min,請大家用平面直角坐標系的方法來表現李雷和韓梅梅離家時間與距離之間的關系。這時教師可以先畫出兩個直角坐標系,用縱坐標表示離家距離,單位為:M;用橫坐標表示離家時間,單位為:min。然后,將例子中提到的相關數據標注在對應的坐標上,如圖1所示。
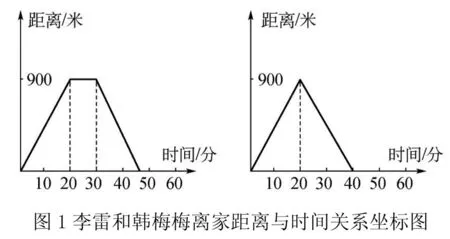
李雷和韓梅梅離家距離與時間關系的例子是生活中最常見的一種數學問題,它主要目的是教會學生會將簡單的距離和時間問題進行數與形的相互轉化,幫助學生利用圖形輕松找到問題的答案,為以后數學學習中的重點和難點知識奠定良好基礎。同時,數形結合的解題思路還應用于統計學中求平均數、眾數和中位數,甚至二次方程求解等問題中。
[1]黃霖明.建構主義在初中數學教學中的應用研究[J].教育觀察,2017,(20) :23.
[2]吳秘.初中數學教學如何激發學生的學習興趣[J].讀與寫,2017,(10) :92.

