約束輪對首次穿越失效的隨機非線性最優控制
劉偉渭,姜瑞金,劉鳳偉,李奕璠,張良威
(1.西南交通大學 機械工程學院,四川 成都 610031;2.中國中車長江車輛有限公司,湖北 武漢 430000;3.西南交通大學 牽引動力國家重點實驗室,四川 成都 610031)
在軌道車輛結構振動的控制中,常以系統響應最小為控制目的,而對受控結構的可靠性或以可靠度最大化為目標的隨機最優控制問題的研究還并不充分[1-3]。對于機械結構而言,所謂可靠性就是系統處于安全域內的概率大小,系統壽命就是結構處于安全域內的時間長度,而系統損壞就是結構首次穿越了原有安全域邊界。這也表明,系統穿越安全域的概率大小、存在于安全域時間的長短對于維持結構安全運行具有較為重要的意義,對于結構系統而言,若能通過外部的控制作用來提高系統可靠性,這對于結構的長期安全運行是一種較為有效的措施[4-8]。
對于高速列車而言,車輛的蛇行失穩、脫軌失效是影響列車長期安全服役安全可靠性的主要因素。車輛蛇行失穩、脫軌失效行為不僅是系統的固有屬性,而且與車輛運行的外部環境也具有重要關系。在線路實際運行時,車輛經常會受到道岔沖擊、強烈的橫風作用、車輛結構件失效以及輪軌接觸關系惡化等因素影響。這將破壞系統原有較為穩定的可靠性性能,使車輛存在安全隱患。對于處于運營中的車輛出現上述失穩等情況,如果只能通過停車或減速運行來處理,將造成較為嚴重的運營事故。基于此,本文以軌道車輛可靠性性能提高為對象,通過隨機非線性控制策略的選取達到對系統穩定性性能改善的具體目標[9-10]。
1 可靠度最大化的隨機非線性最優控制方法
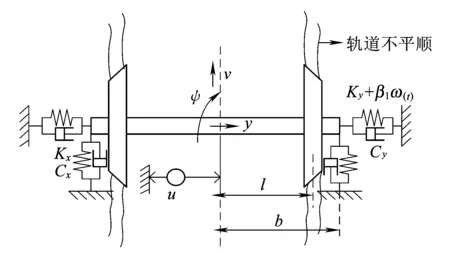
考慮受控作用下的擬不可積Hamilton系統結構,受控平均It微分方程為
( 1 )
其中,
( 2 )
若原系統的正常運行區域為[0,Hc),[0,∞)為Hamilton函數取值范圍,H(0)=H0∈[0,Hc)為系統初值,為了提高系統可靠性,可定義最優成本函數
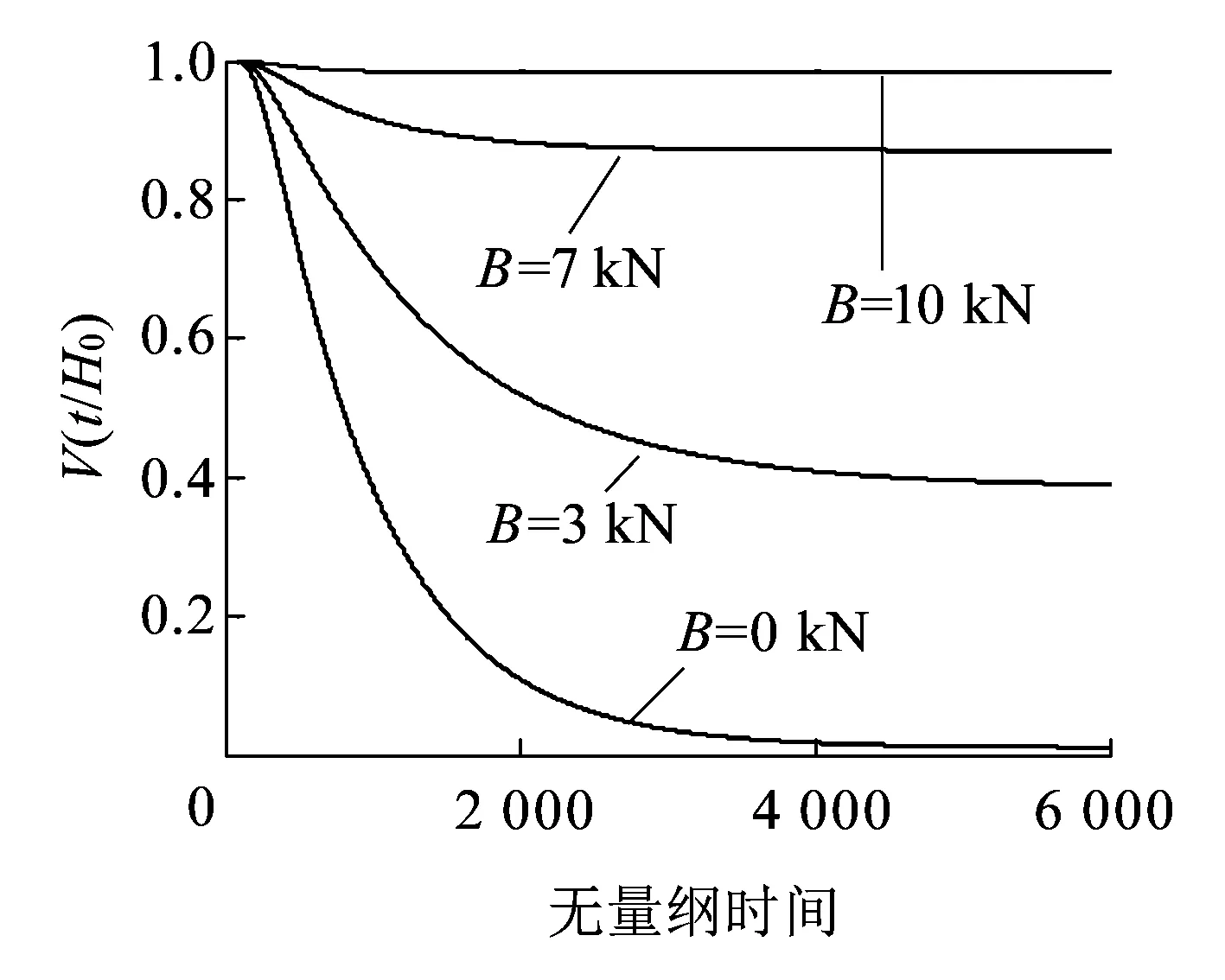
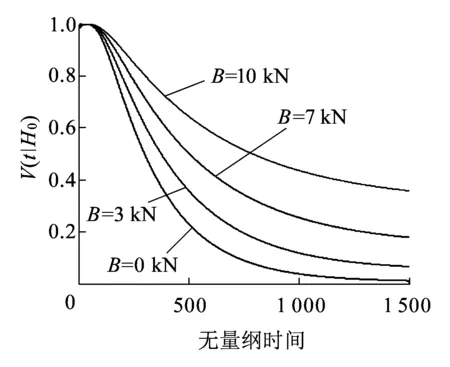
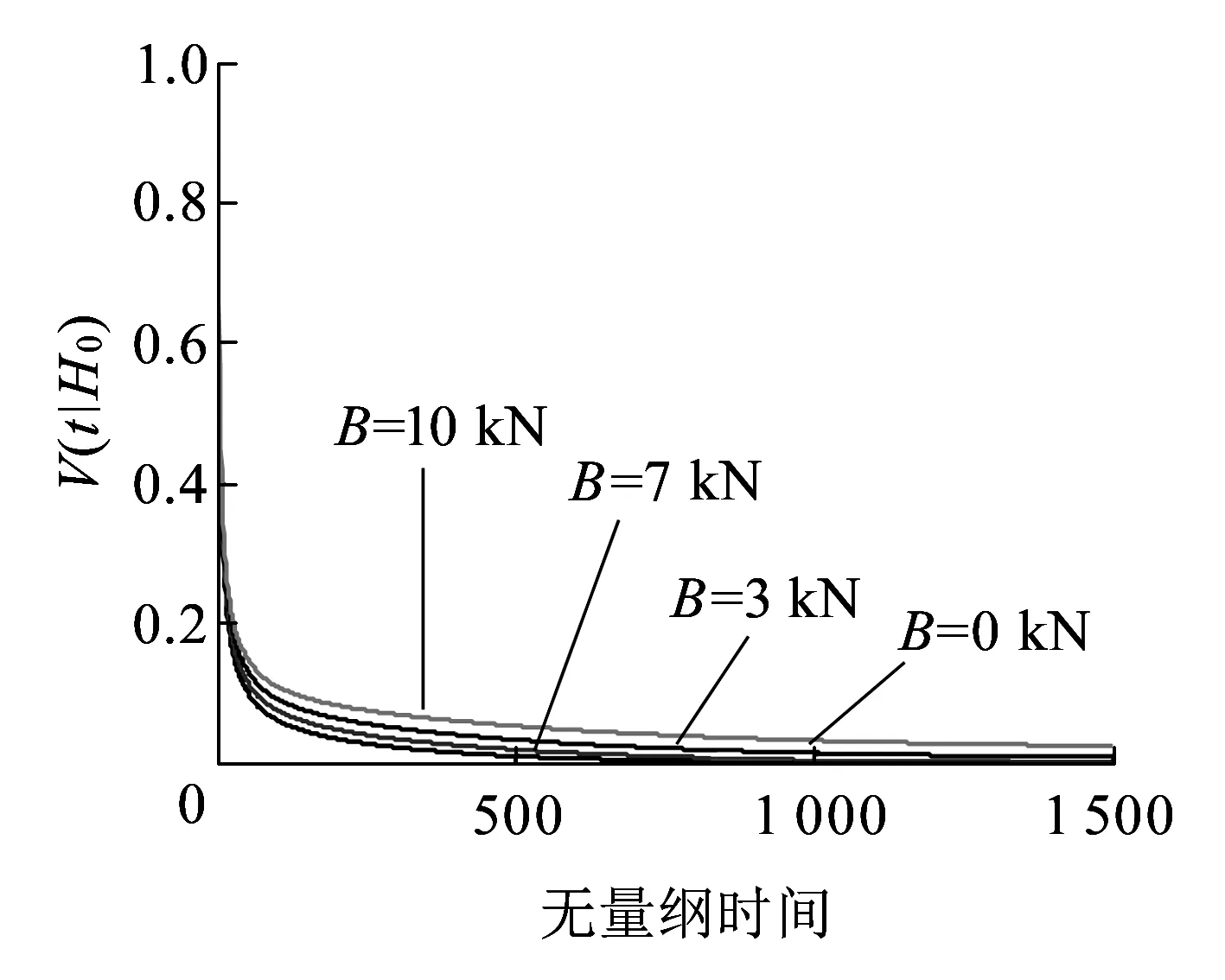
t ( 3 ) 首次穿越時刻為τ;控制終時時刻為tf≤τ;受控約束條件為u∈U。此時作為可靠度最大化為控制目標的動態規劃方程為 0≤t≤tfH∈[0,Hc) ( 4 ) 其中的邊界條件為 V(Hc,t)=0 ( 5 ) V(0,t)=有限 ( 6 ) 終值條件為 V(H,tf)=1H∈[0,Hc) ( 7 ) 式( 4 )~式( 7 )即為受控條件下原系統可靠度最大化的首次穿越數學方法。 把方程( 4 )的動態規劃方程右邊對ui進行極大值分析,得到原系統的最優控制率條件。假如約束條件為 |ui|≤bii=1,2,…,n ( 8 ) 其中,bi是定值,可以看出,當|ui|=bi,并且ui的數值能使ui(?H/?Pi)(?V/?H)得到正值,此時的式( 4 )右邊即可得極大值,則控制率為 ( 9 ) 因為可靠性函數在任何初值下均是單調遞減函數,即?V/?H<0,這樣式( 9 )可簡化為 (10) (11) 其中, (12) 0≤t≤tfH∈[0,Hc) (13) 式(13)的邊界控制條件和終值控制條件為式( 5 )~式( 7 )。此時的條件可靠性函數為 Rc(t1|H0)=P{H(s,u*)∈[0,Hc), s∈(0,t1]|H(0)∈[0,Hc)} (14) 滿足后向Kolmogorov方程 (15) Rc(t1|Hc)=0 (16) Rc(t1|0)=有限 (17) 初始條件為 Rc(0|H0)=1H0=∈[0,Hc) (18) 原系統首次穿越損壞條件的概率為 (19) 首次穿越時間τ具有的條件概率密度為 (20) 為分析更為接近軌道車輛的實際運行工況,考慮如圖1所示的約束輪對模型,在該模型中考慮了一系懸掛剛度參數激勵影響以及來自鋼軌的隨機不平順激勵作用。本文重點關注系統的橫向失穩可靠性以及控制策略的有效性,由于垂向懸掛對橫向運動耦合影響較小,為便于直觀分析,只考慮橫向模型。 圖1 受控的彈性約束輪對模型 上述模型中各參數和具體數值見表1。 表1 各參數及數值 受控約束輪對系統運動方程為 (21) 假設有變量代換 a=a1+a2β01=β11+β12 β02=β13+β14β03=β23+β24 原系統的Hamilton函數為 (22) 式(21)可改寫為 (23) 其中, m11(q1,p1)=a1m12(q1,p2)=0 f1(q1)=β11q1+β12q1+β13+β14 f2(q1)=β22q1+β23+β24 式(23)為受控約束輪對隨機激勵耗散Hamilton方程組。 約束輪對系統受控條件下其求解過程服從一維擴散過程,而該過程被平均It微分方程所支配。 (24) D((β13+β14)2+(β23+β24)2) (25) D((β13+β14)2+(β23+β24)2)H (26) 根據式(10)有 (27) 式( 1 )中的ui由式(29)的最優控制率u*取代,進行平均則有 (28) 把式(28)代入式(24),受控條件下的漂移系數為 (29) 把式(29)和式(26)分別代入式(13)和式(15),即可得到可靠度最大化為控制目標的首次穿越時間條件概率密度以及最優動態規劃方程。 方程(13)為二階變系數拋物線與雙曲線組合型偏微分方程,對其的求解采用有限差分法Peaceman-Rachford,初始能量H0=0.02,各參數值見表1。 圖2為不同控制力幅值下系統可靠性隨時間的變化情況,其中橫坐標為系統運行的無量綱時間,縱坐標的可靠性函數值表示系統處于安全域內的概率值,當縱坐標為0時表示系統必將穿越安全域而發生失穩脫軌,當縱坐標為1時表示系統始終處于安全域內,當縱坐標為(0,1)時,表示系統處于安全域內,只是具有一定概率值。從圖2可以看出,當系統沒有受到控制約束作用時,即B=0,此時輪對系統的可靠性函數值隨著運行時間的增加,逐漸減小,并最終趨于恒定值零。當受到控制約束作用后,控制力為3 kN和7 kN時,仍然具有上述規律,但是此時可靠性函數的最終恒定值隨著控制力的作用逐漸增加。特別地,當控制力增加為10 kN時,可靠性函數值幾乎沒有減小趨勢,而始終恒定于1。總體來看,約束輪對系統在該控制策略下,穩定性的可靠性性能改善明顯,在此參數條件下,原系統不穩定,受控后可改變系統的穩定性,使原不穩定性系統變為概率意義上的穩定系統,特別是當控制力達到某一幅值后,系統將轉變為絕對意義上的穩定系統。 圖2 不同控制力幅值下系統可靠性隨時間的變化情況 圖3為不同控制力幅值下系統首次穿越時間概率密度隨時間變化情況,其中橫坐標為系統運行的無量綱時間,縱坐標的首次穿越時間條件概率密度表示系統在對應的運行時刻點上穿越出安全域的概率值,數值越小系統越能維持于安全域內。從圖3可以看出,隨著運行時間的增加,不管是否受控,系統均呈現出首次穿越時間條件概率密度先逐漸增加,達到某一峰值后再逐漸減小,并最終趨于一恒定值。未受控時(即B=0),在時刻t=110,具有最大概率值;受控后,隨著控制力從3、7、10 kN逐漸增加,最大概率幅值逐漸減小,但是出現最大概率幅值所對應時刻幾乎也在t=110。總體來看,在該控制策略作用下,系統發生首次穿越的概率會隨著控制力的增加逐漸減小,而使系統變得更為穩定,然而控制作用卻不能改善或延遲系統發生首次穿越的時刻。 圖3 不同控制力幅值下系統首次穿越時間概率密度隨時間變化情況 為分析在不同系統初始能量激勵下隨著控制約束的變化影響,得到了圖4、圖5的結果。圖4初始能量H0=0.04,圖5初始能量H0=0.08,二者的控制約束力分別為0、3、7、10 kN。由圖4可以看出,隨著輪對運行時間t的增加,可靠性函數值的變化規律為先從1逐漸減小,并最終趨于介于0~1之間的一個恒定值。當未控時(B=0 kN),可靠性函數值最終趨于0,表明系統隨著運行時間的增加將失效;而當控制力從3 kN變化到10 kN時,可靠性函數的穩定值逐漸增加,表明系統隨著運行時間的增加不會失效,并且控制力越大系統失效的可能性越小。由圖5可以看出,當初始能量較大時,隨著輪對運行時間的增加,系統在較短時間內,可靠性函數值迅速從1減少為一個接近于0的穩定值。當控制力從0、3、7、10 kN逐漸增加時,可靠性函數的恒定值只是略有增加,控制效果幾乎不起作用。這表明,當輪對運行具有較大初始激勵能量時,系統將快速失穩并脫軌失效,這是由于輪對失穩的振動為發散運動,系統的能量逐漸增加,并最終超過輪軌約束而脫軌,即使此時提供約束控制,效果也不明顯。 圖4 不同控制力幅值下系統的可靠性隨時間變化情況(H0=0.04) 圖5 不同控制力幅值下系統的可靠性隨時間變化情況(H0=0.08) 為分析約束輪對首次穿越失效后的最優控制,并改善系統的穩定性性能,建立受控動力學模型中考慮軌道不平順激勵和自身結構參激的動力學模型。基于隨機動態規劃原理的控制策略,并運用擬不可積Hamilton系統隨機平均法,以可靠度最大化為控制目標,建立可靠性函數和首次穿越時間概率密度函數的動態規劃方程。 分析表明,通過控制力作用,可使原本不穩定的系統在受控后變為概率意義上的穩定系統,在選取適當控制力條件下,甚至可使可靠性函數值接近于1,而使系統成為絕對意義上的穩定系統。另外,在系統失穩初期,并未激發較大能量時,即使提供較小的外界控制約束力作用,也能達到較好效果;如果系統失穩,經過一段時間而激發了較大振動能量,此時再提供約束作用,對改善系統性能已不明顯。 上述內容僅針對單輪對隨機最優控制的理論分析,為了分析的完整性,還應增加試驗驗證對比。在后續研究中,將繼續完成軌道車輛整車隨機最優控制理論和仿真分析,把具有二系橫向作用器裝置的整車在滾振臺上進行試驗,并與理論分析進行比較和驗證。 參考文獻: [1]曾京,戴煥云,鄔平波.基于開關阻尼控制的鐵道客車系統的動力學性能研究[J].中國鐵道科學,2004,(25)6:28-32. ZENG Jing,DAI Huanyun,WU Pingbo.Dynamics Perform-ance Study of Railway Passenger Car System Based on On/Off Damping Control[J].China Railway Science,2004,(25)6:28-32. [2]歐陽冬,張繼業,張衛華.鐵道車輛自供能量橫向主動懸掛系統[J].交通運輸工程學報,2008,8(1):15-18. OUYANG Dong,ZHANG Jiye,ZHANG Weihua.Self-powered Active Lateral Suspension System of Railway Vehicle[J].Journal of Traffic and Transportation Engineering,2008,8(1):15-18. [3]佐佐木君章.改善高速列車的橫向乘坐舒適度——半主動懸掛減振裝置的應用[J].鐵道學報,2004,26(1):105-115. KIMIAKISASAKI.Improving Lateral Ride Comfort of High-spped Trains Applying Semi-active Suspension Sytem to High Speed Trains[J].Journal of The China Railway Society,2004,26(1):105-115. [4]許佳,王洪禮,葛根.柔性梁在軸向隨機激勵作用下的可靠性與最優控制[J].天津大學學報,2009,42(8):739-743. XU Jia,WANG Hongli,GE Gen.Reliability and Optimal Control on Flexible Suffered Axial Randomly Excitation[J].Journal of Tianjin University,2009,42(8):739-743. [5]CHEN L C,ZHU W Q.First Passage Failure of Quasi-partial Integrable Generalized Hamiltonian Systems[J].International Journal of Non-Linear Mechanics,2010,45(1):56-62. [6]張巍,應祖光,胡榮春.不確定性拉索非線性隨機振動的最優控制[J].噪聲與振動控制,2014,34(1):44-46. ZHANG Wei,YING Zuguang,HU Rongchun.Optimal Control of Nonlinear Random Vibration of an Inclined Taut Cable with Uncertainties[J].Noise and Vibration Control,2014,34(1):44-46. [7]葛根,王洪禮,許佳.隨機最優控制下矩形薄板受面內隨機參數激勵的首次穿越研究[J].振動與沖擊,2012,31(4):179-183. GE Gen,WANG Hongli,XU Jia.Stochastic Stability and First Passage Failure of Thin Rectangular Plate Subjected to Stochastic Parametrical Excitation[J].Journal of Vibration and Shock,2012,31(4):179-183. [8]孫燕軍,冷小磊.公路橋梁車輛耦合系統隨機最優控制研究[J].應用力學學報,2012,29(3):335-340,359. SUN Yanjun,LENG Xiaolei.Research on Stochastic Optimal Con-trol of Highway Bridge Vehicle Coupling System[J].Chinese Journal of Applied Mechanics,2012,29(3):335-340,359. [9]凌亮,肖新標,吳磊,等.地震波頻譜特性對高速列車動態脫軌行為的影響[J].工程力學,2013,30(1):384-393,431. LING Liang,XIAO Xinbiao,WU Lei,et al.Effect of Spectrum Characteristics of Seismic Wave on Derailment of High-speed Train[J].Engineering Mechanics,2013,30(1):384-393,431. [10]關慶華,曾京.輪軌橫向碰撞引起的脫軌研究[J].振動與沖擊,2009,28(12):38-42. GUAN Qinghua,ZENG Jing.Study on Derailment Induced by Lateral Impact between Wheel and Rail[J].Journal of Vibration and Shock,2009,28(12):38-42.
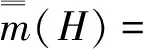
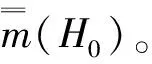
2 受控約束輪對系統模型

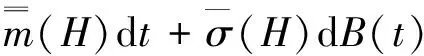

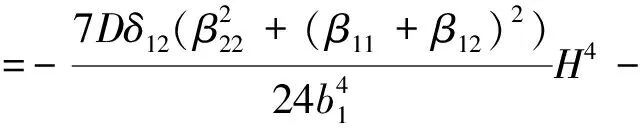
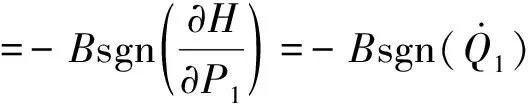
3 數值仿真結果

4 結束語

