基于導波多模態融合的無縫鋼軌溫度應力估計算法

王 嶸，余祖俊，朱力強，許西寧

(1.北京交通大學 機械與電子控制工程學院，北京 100044；2.北京交通大學 載運工具先進制造與測控技術教育部重點實驗室，北京 100044)

我國高速鐵路規模的不斷增大對高速鐵路運行安全提出了更高要求。高速鐵路通常采用的無縫鋼軌線路在長度方向上不能自由伸縮，當鋼軌溫度發生變化時，其內部將產生較大的溫度應力，嚴重時會導致脹軌、跑道及斷軌等事故的發生，直接威脅行車安全。因此，在線監測無縫鋼軌內部縱向溫度應力并在超限前預警，對保障高速鐵路的安全運營具有重要意義。

超聲導波對應力敏感，在鋼軌中傳播時可引起鋼軌橫截面內全部質點振動，受鋼軌表面殘余應力的影響較小，已經成為檢測鋼軌縱向溫度應力的一種重要方法。文獻[1]通過對桿和平板的研究發現，隨著應力增大，導波的相速度增大、群速度減小，通過測量群速度或相速度可對應力進行檢測。文獻[2]推導一維彈性波導介質在軸向應力作用下的波動方程，并分析應力作用下導波的傳播特性。文獻[3]獲得鋼絞線低頻率段模態的群速度與拉應力標定曲線，通過測定鋼絞線中該模態的群速度就能計算出鋼絞線的應力值。文獻[4]采用半解析有限元方法分析軸向拉應力作用下鋼軌水平彎曲模態、垂直彎曲模態和扭轉模態在1 kHz以內相速度的變化趨勢。文獻[5]選取一種對應力敏感的35 kHz導波模態，獲得該模態在不同應力下的群速度標定曲線，通過測定鋼軌中該導波的群速度即可計算鋼軌溫度應力。

以上基于超聲導波的應力檢測技術研究都假設波導體的彈性模量是常數，實際服役中的無縫鋼軌，當環境溫度變化時，其彈性模量將發生明顯變化。文獻[6]推導在溫度發生變化時，鎖定鋼軌彈性模量和溫度應力變化對相速度的影響，發現前者的影響比后者大一個數量級。為了準確測量溫度應力，需首先獲得鋼軌的應力-相速度-彈性模量三維標定曲面。這種方法在工程中難以實現，因為獲取該曲面的工作量大且較繁瑣，在使用時還需要同時測量鋼軌彈性模量和相速度。因此，如何消除彈性模量的影響是目前急需解決的技術難題。本文利用鋼軌多個導波模態的相速度(或者波數)對應力和彈性模量敏感程度不同的特性，提出一種多模態融合估計算法，克服彈性模量變化對應力檢測的影響，在彈性模量未知的條件下估計鋼軌溫度應力。

1 理論基礎

由聲彈性原理可知，應力σ與波數ξ以及彈性模量E之間存在函數關系。已知波數ξ和彈性模量E時，利用此函數估計應力σ，記為

σ=f(ξ，E)

( 1 )

此時，應力的誤差傳遞函數為

( 2 )

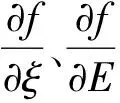
為了評估此方法的可行性，通過半解析有限元方法對有初始應力的鋼軌進行建模，求解函數f及Δσ。

1.1 有初始應力的鋼軌半解析有限元建模

對于規則橫截面的波導介質，可以建立解析解的頻散方程，研究其導波的傳播特性。鋼軌橫截面較復雜，無法建立解析解的頻散方程。半解析有限元方法是國際上普遍采用的求解任意橫截面波動方程的一種有效方法，其基本原理是在波導介質的橫截面上進行有限元離散，沿波導介質傳播方向的位移用簡諧波的振動方式表示，根據哈密爾頓原理可以推導出導波在其中傳播的波動方程[7]。

我國高速鐵路廣泛使用60 kg/m鋼軌，其截面如圖1所示，定義其橫截面為y-z平面，波傳播方向為x方向。

圖1 采用三角形單元離散的60 kg/m鋼軌y-z橫截面

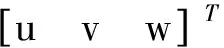
( 3 )

( 4 )

假定導波沿x方向傳播時波導介質做簡諧振動，其中任意一點的位移可用空間分布函數表示為

( 5 )

式中：ω為導波角頻率；t為時間參數。

ε=[εxxεyyεzzεxyεyzεzx]T=

( 6 )

采用半解析有限元法分析鋼軌中導波的傳播特性，可得到60 kg/m鋼軌中超聲導波的波動方程[7]為

( 7 )

當波導介質存在較大的初始應力σ(0)時，必須考慮初始應變與位移的二次項，即非線性應變-位移關系。有初始應力時，應變S與位移u的關系為

( 8 )

單位體積的應變能φ可表示為

( 9 )

(10)

式中：Sxx為x方向的非線性應變。式(10)中省略部分為高階無窮小量。

(11)

(12)

初始應力作用下波導介質總體積應變能為

(13)

因此，含有軸向初始應力的鋼軌波動方程[9]為

(14)

1.2 波數與彈性模量測量精度對應力測量精度的影響

將式(14)移項，并令

G(ξ，σ，E)=[ξ2·(K2+K(0))+ξ·K1+

(15)

式中：σ為縱向溫度應力；G(ξ，σ，E)為關于ξ、σ、E的函數。

根據隱函數求導公式，求解出應力對波數的偏導數為

(16)

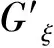
根據隱函數求導公式，應力對彈性模量的偏導數為

(17)

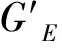
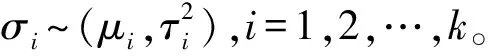
σ=α1f1(ξ1，E1)+α2f2(ξ2，E2)+…+

(18)

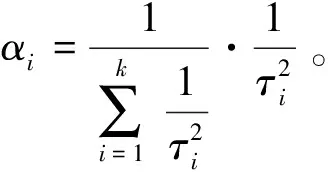
多模態融合估計應力誤差傳遞函數為

(19)

仿真試驗數據表明，波數測量誤差導致的應力誤差為0.243 5 MPa。若使應力估計誤差在2 MPa以內，根據式(19)可知，彈性模量的測量誤差應在0.011 13 GPa以內，相對誤差為0.005 3%。這個量級的測量精度在對彈性模量的實際測量中是難以達到的。因此，采用傳統的補償彈性模量方式不可取，本文利用不同模態對彈性模量的敏感度不同這一特點，抵消彈性模量對應力估計結果的影響。

2 基于多模態融合的應力估計方法

通過半解析有限元程序計算特定頻率下各個模態對溫度應力和彈性模量的敏感性，定量分析兩者對相速度的影響。利用應力和彈性模量對相速度敏感程度不同這一特性，基于應力估計值最小原則選出特定的模態對應力進行估計。最后，通過數據驗證方法的正確性。

2.1 多模態對應力與彈性模量敏感度分析

在特定頻率下，各個模態對溫度應力和彈性模量敏感程度的判斷有兩種方法。一是通過導波模態的振型判斷。現有研究結果表明，水平彎曲模態和扭轉彎曲模態對應力敏感，伸展模態對彈性模量敏感。因此只要利用有限元方法獲得導波模態的振型，根據主要振動形態即可大致估計其對應力與彈性模量的敏感程度。二是通過對比應力和彈性模量變化前后的頻散曲線判斷。例如，對比應力變化前后，特定頻率下各個模態相速度的變化率，前后狀態變化率最大的是對應力最敏感的模態；模態對彈性模量變化的敏感程度同理。第二種方法可以定量分析各模態對溫度應力和彈性模量的敏感性，因此本文采用第二種方法論述。

對于60 kg/m鋼軌，溫度變化1 ℃大約等效于彈性模量變化0.05 GPa，鎖定狀態下溫度應力變化2.5 MPa[9]。假設室溫為20 ℃時，彈性模量為210 GPa，應力為0 MPa。若溫度的變化范圍為-20～60 ℃，則應力變化范圍為-100～100 MPa，彈性模量變化范圍為208～212 GPa。以35 kHz為中心頻率作為激勵信號，計算出3種狀態下各模態的相速度(當頻率一定時，相速度與波數成反比，求解相速度等價于求解波數)：第一種狀態為彈性模量210 GPa、應力0 MPa；第二種狀態為彈性模量210 GPa、應力100 MPa；第三種狀態為彈性模量212 GPa、應力0 MPa。3種狀態下不同模態相速度對比見表1。從表1可以看出，1號模態對溫度應力最敏感，20號模態最不敏感；19號和20號模態對彈性模量最敏感，1號模態最不敏感。說明當彈性模量一定時，隨著相速度值增大，模態對溫度應力敏感度減小；當溫度應力一定時，隨著相速度值增大，模態對彈性模態敏感度增大。從總體上看，不同模態對溫度應力和彈性模量的敏感程度不同。第一種與第三種狀態相速度變化率明顯大于第一種與第二種狀態相速度變化率，即在溫度變化工況下彈性模量比溫度應力對波數的影響更大。

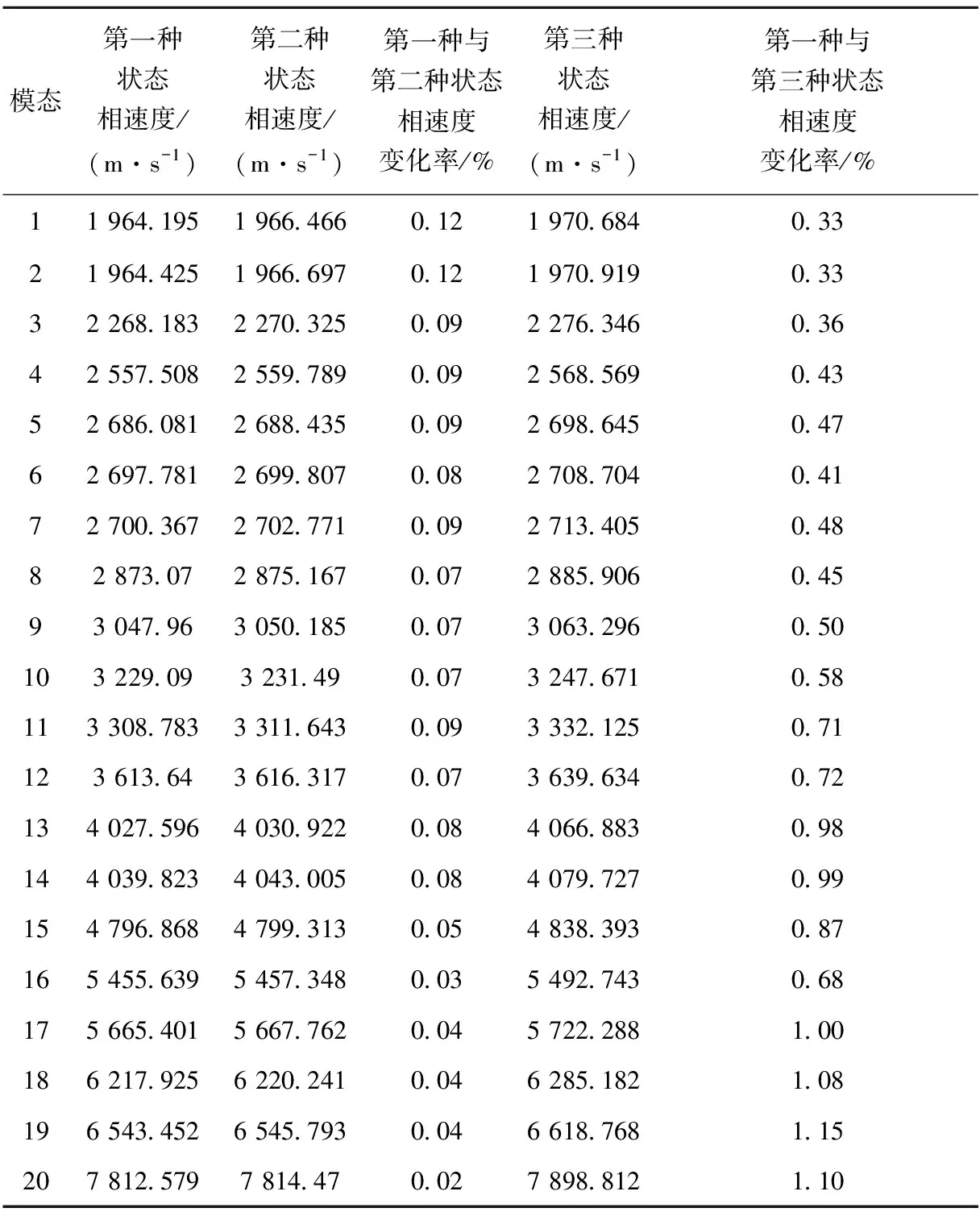
表1 35 kHz導波在不同彈性模量狀態和不同溫度應力作用下在鋼軌中傳播的相速度對比

2.2 多模態估計方法

為了消除彈性模量測量對應力測量的影響，提高應力估計精度，采用應力估計最小誤差的方法選取多模態組合對應力進行估計。假設波數ξ與溫度應力σ和彈性模量E之間存在線性函數關系g，波數ξ表達式為

ξ=g(σ，E)=aσ+bE+η

(20)

式中：a、b、η為系數，其表達式分別為

(21)

(22)

當溫度應力σ和彈性模量E一定時，相應的參數a、b、ξ均可通過式(21)、式(22)計算出來，則參數η為

η=ξ-aσ-bE

(23)

當選取了k個模態，式(20)可改寫為

ξi=gi(σ，E)=aiσ+biE+ηi

i=1，2，…，k

(24)

將式(24)改寫成矩陣形式為

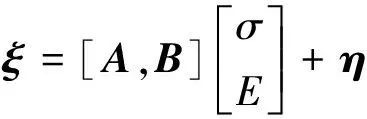
(25)

式中：ξ=[ξ1ξ2…ξk]T，A=[a1a2…ak]T，B=[b1b2…bk]T，η=[η1η2…ηk]T。

根據最小二乘法，溫度應力σ以及彈性模量E的估計量表達式為

(26)

表2 不同彈性模量狀態下不同模態組合對零應力的估計值

3 仿真試驗驗證

基于以上理論，實際測量溫度應力分為兩步。第一步，獲得波數-應力標定函數。利用半解析有限元法建立60 kg/m鋼軌模型。在鋼軌模型的特定節點施加激勵信號，如正信號或漢寧窗調制的正弦信號，通過解析求解得到遠處某一點的振動響應。通過改變模型中溫度應力和彈性模量參數獲取不同溫度應力與不同溫度狀態下導波振動響應，采用二次加權算法計算各個模態波數。通過BP神經網絡建立波數與應力的標定函數。限定溫度參考的范圍可以提高應力估計精度，因此引入軌溫作為特征參數。BP神經網絡的輸入信號是各模態的波數和軌溫，輸出信號是溫度應力。第二步，在測量應力時，采集陣列數據和軌溫，計算各模態波數，代入標定函數，估計溫度應力。為了驗證本文理論的可行性，采用仿真試驗進行驗證。

3.1 鋼軌建模

導波在波導體中的傳播特性一般用頻散曲線c-f描述，其中f為導波信號的頻率，c為導波相速度Cp。對于鋼軌這類具有復雜不規則截面的波導體，頻散曲線無法通過解析式描述，只能借助仿真方法(如半解析有限元法[7-8，10])獲得數值解。

圖2為采用半解析有限元法獲得的60 kg/m鋼軌在零應力狀態下的相速度頻散曲線，其中，鋼軌彈性模量為E=210 GPa，泊松比為ν=0.3，密度ρ=7 800 kg/m3。從圖2可以看出，在低頻段，鋼軌中主要存在4個導波模態；隨著頻率的增加，能夠在鋼軌中傳播的導波模態也越來越多。圖2表明，鋼軌中的導波具有頻散特性，即對于同一導波模態，頻率變化時，導波的速度也發生變化，這將造成波形在傳播過程中發生畸變。

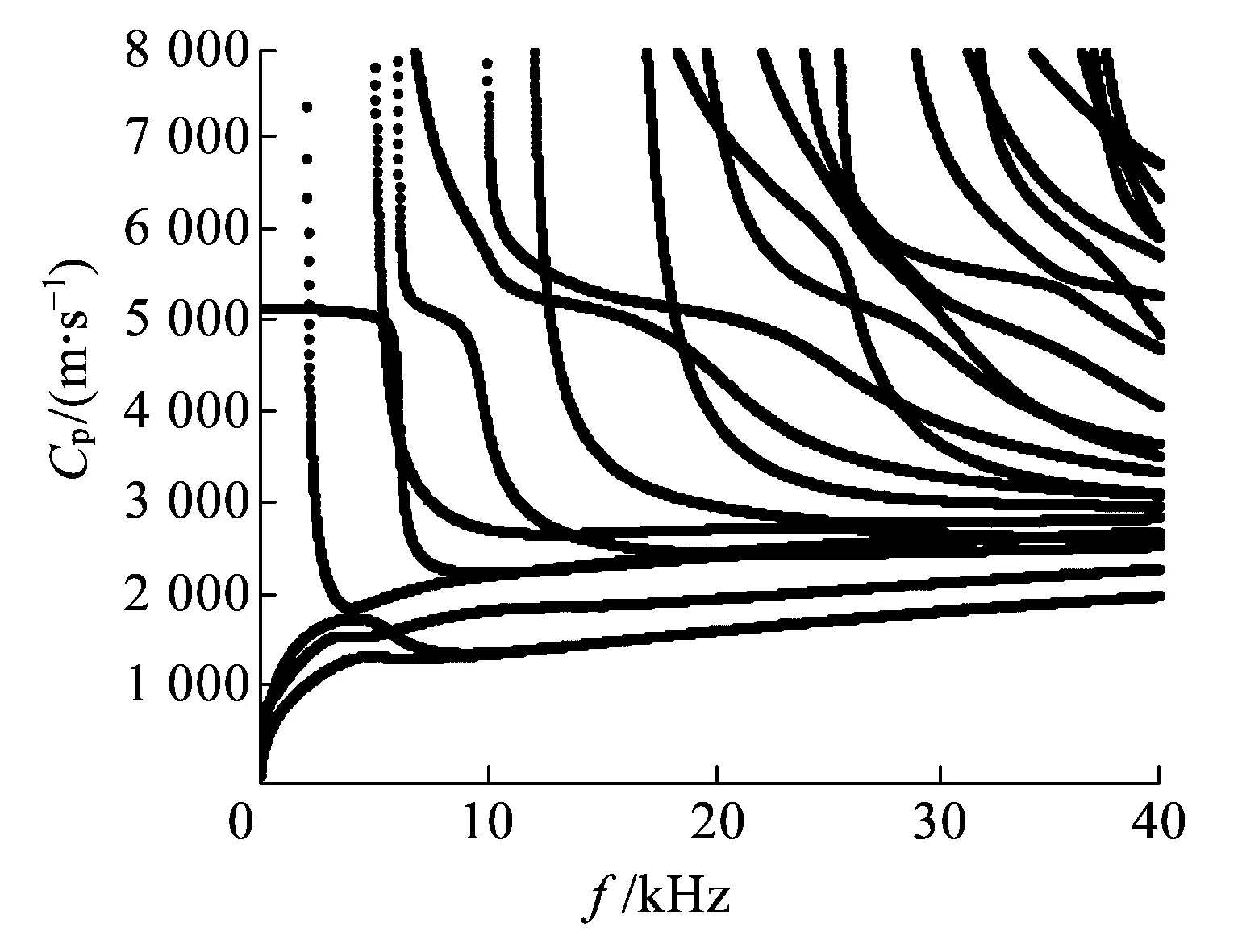
圖2 零應力狀態下60 kg/m鋼軌相速度頻散曲線

當鋼軌中存在拉應力或壓應力時，導波的傳播速度將發生改變。例如，鋼軌中拉應力為100 MPa時，在如圖3所示的低頻段范圍內(0～1 kHz)，各模態的相速度發生了微小變化，且各模態的變化程度(對溫度應力的敏感度)不同。相速度值增加時，其對溫度應力的敏感性逐漸減弱。

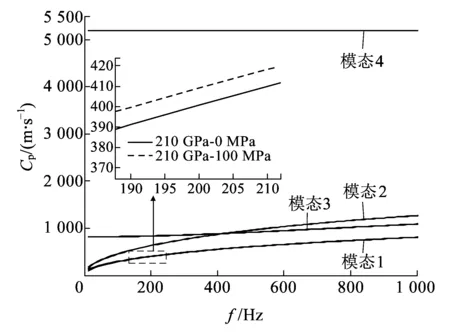
圖3 彈性模量為210 GPa時不同應力狀態下的相速度頻散曲線

當鋼軌彈性模量變化時，導波的傳播速度將發生改變。例如，在零應力狀態下，鋼軌的彈性模量由210 GPa變為212 GPa時，在如圖4所示的低頻段范圍內(0～1 kHz)，各模態的相速度發生了微小變化，且各模態的變化程度(對彈性模量的敏感度)不相同。相速度增加時，其對彈性模量的敏感性逐漸增強。

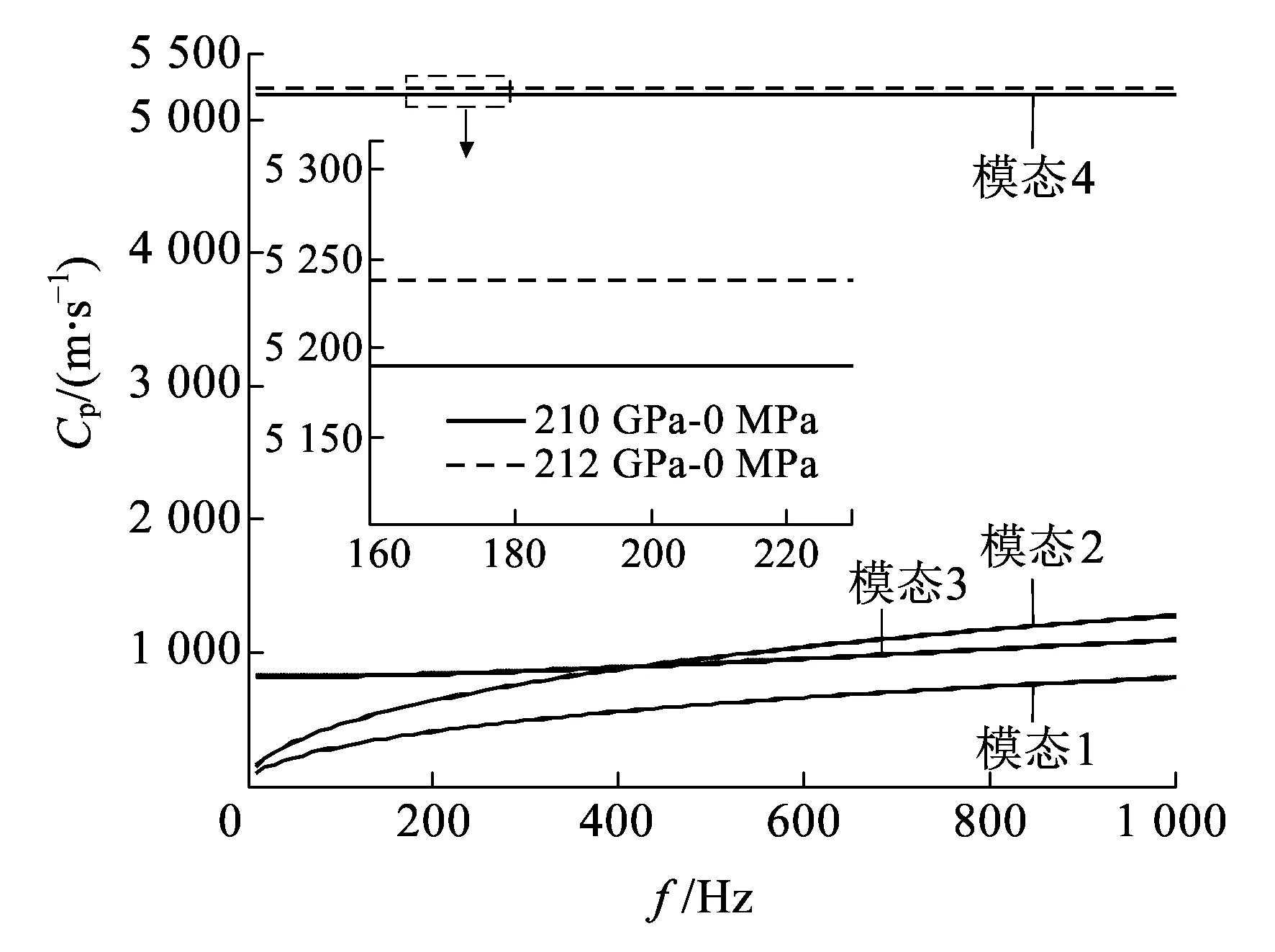
圖4 零應力時不同彈性模量狀態下的相速度頻散曲線

3.2 模態激勵與波數測量方法

在35 kHz頻率下，首先挑選對溫度應力敏感的模態和對彈性模量敏感的模態，同時應便于激勵與接收、信號模態相對單一。通過模態振型分析，確定每一個模態的最佳激勵與接收位置、方式，獲取不同溫度應力與不同彈性模量狀態下的導波信號。最后，通過二次加權算法計算各個模態波數。在35 kHz頻率下選擇了模態1、模態3、模態7、模態20。設置11種溫度應力狀態，即在-100～100 MPa范圍內，每間隔20 MPa設置一個狀態點；設置5種彈性模量，在206～214 GPa范圍內，每間隔2 GPa設置一個狀態點。

模態1為水平彎曲模態，波長約為0.056 12 m，溫度應力變化時在20個模態中群速度與相速度變化率最大，對溫度應力最敏感。通過振型分析，選擇在軌底4號節點施加z方向的激勵，4號節點x方向設置信號接收點。激勵信號設置成以35 kHz為中心頻率、漢寧窗調制的5個周期正弦波。從距離激勵位置2 m處開始，每間隔0.02 m設置一個數據采集點，共有128個同步采集點。每個采集點的采樣頻率為1.4 MHz，采樣點數為4 096。2、3、4、5 m處接收到的位移信號時域波形如圖5所示。從圖5可以看出，隨著傳播距離的增加，信號的波包峰值降低，波形寬度變大，波形在傳播過程中發生了畸變。

(a)距激勵位置2 m處

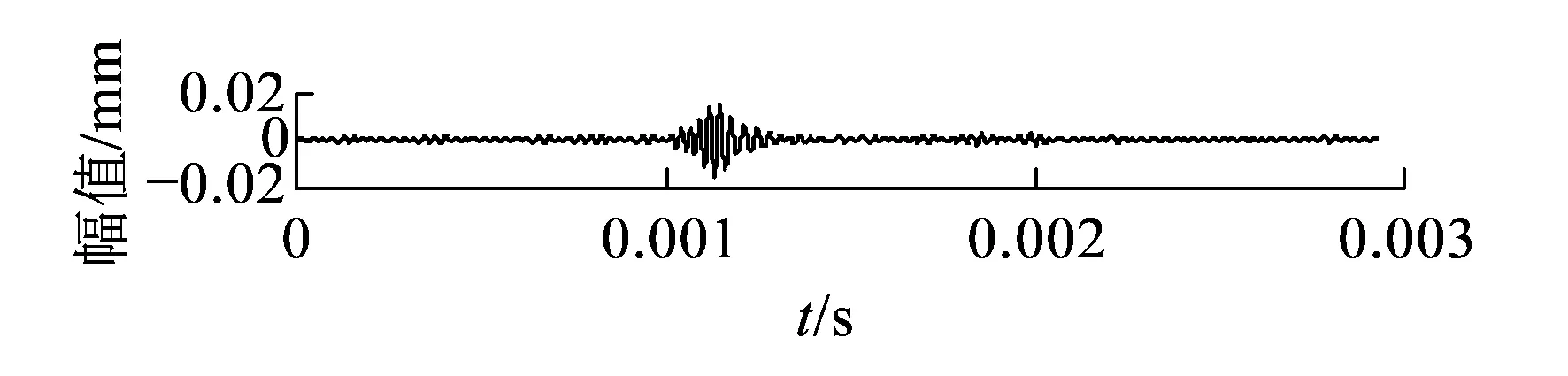
(b)距激勵位置3 m處

(c)距激勵位置4 m處

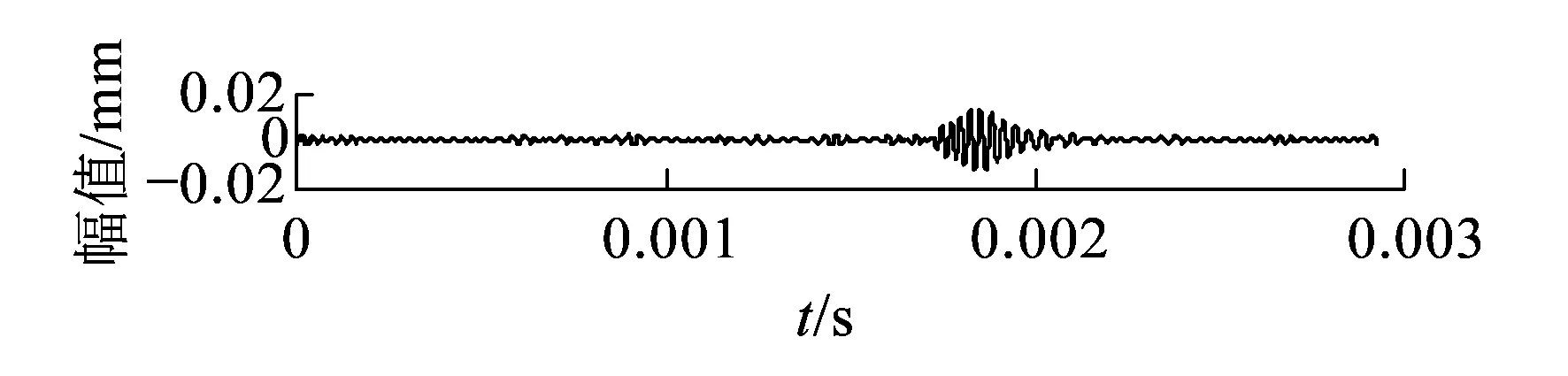
(d)距激勵位置5 m處圖5 4號節點不同位置位移信號時域波形

模態3為扭轉彎曲模態，波長約為0.064 81 m，溫度應力變化時在20個模態中群速度與相速度變化率排第三位。通過振型分析，選擇在軌腰36號節點施加y方向的激勵，36號節點x方向設置信號接收點。模態7的振型比較復雜，其波長約為0.077 15 m，相對于其他模態更容易被激勵出來。通過振型分析，選擇在軌頂41號節點施加x方向的激勵，41號節點z方向設置信號接收點。模態20為伸展模態，波長約為0.223 2 m，彈性模量變化時在20個模態中群速度與相速度變化率最大，對彈性模量最敏感。通過振型分析，選擇在軌頂64號節點施加x方向的激勵，64號節點x方向設置信號接收點。

分別對模態1、模態3、模態7、模態20的128點數據做二維傅里葉變換，在彈性模量210 GPa、應力0 MPa狀態下處理結果如圖6所示，通過頻率和波數計算各模態的相速度約分別為1 960.19、2 252.96、2 731.06、7 510.40 m/s，與理論計算的模態速度相符。

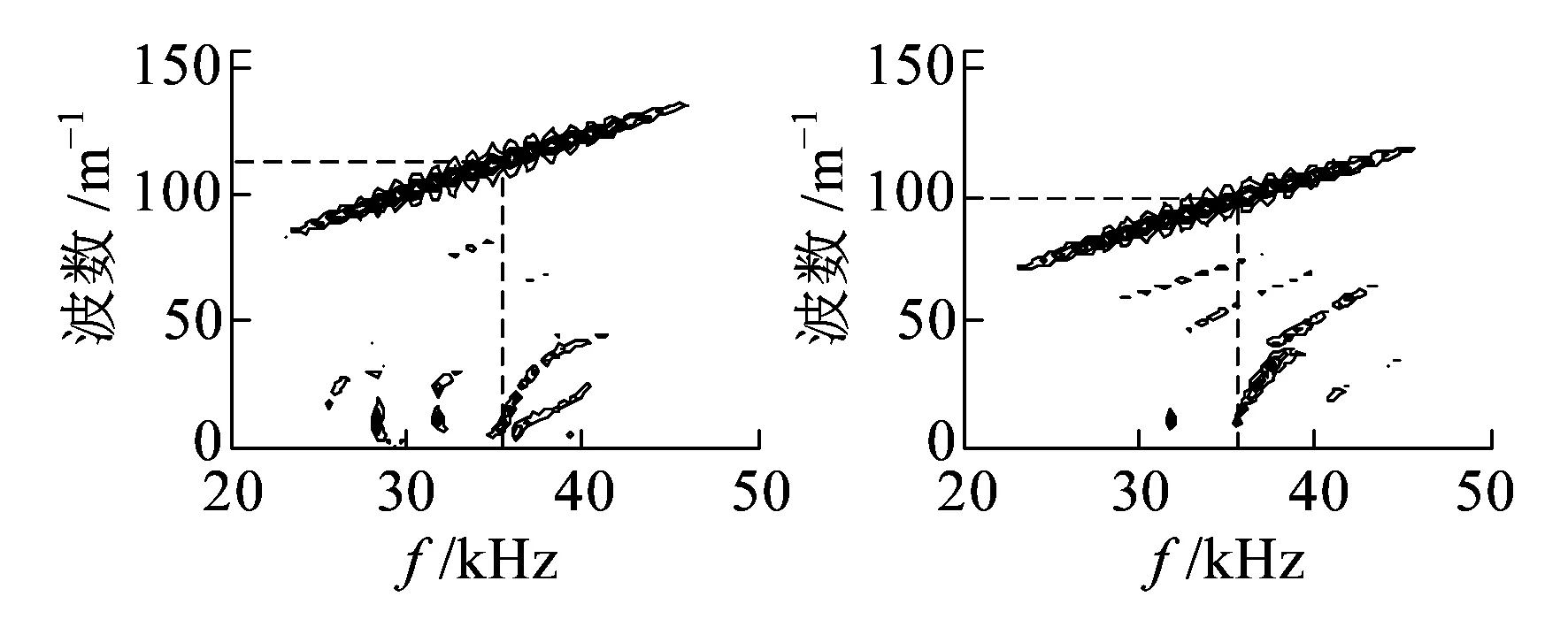
(a)模態1 (b)模態3

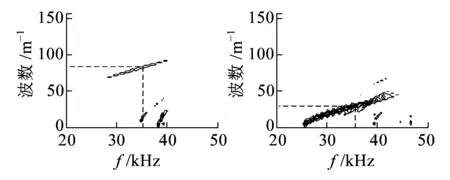
(c)模態7 (d)模態20圖6 零應力下35 kHz導波不同模態的二維傅里葉變換結果

二維傅里葉變換后的波數結果存在量化誤差，大致估算的相速度值可用于模態辨識，應力檢測則需要高精度的波數。因此，通過頻率和二次加權修正波數計算該模態的波數[11]。根據類似于三角形重心坐標的加權公式，頻率-波數加權點位置如圖7所示。選取距離激勵頻率f最近的兩個傅里葉變換量化頻率f1和f2，選取波數ξ附近3個波數ξ1、ξ2、ξ3，同時可以得到6個點s11、s12、s13、s21、s22、s23對應的等高線幅值l11、l12、l13、l21、l22、l23。

圖7 頻率-波數加權點位置示意

使用等高線幅值歸一化對單個頻率下波數進行加權修正得到

(27)

(28)

(29)

3.3 多模態融合應力估計結果

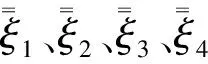
模型標定數據選取5種彈性模量和11種溫度應力狀態下的波數。假設溫度變化1 ℃約等效于彈性模量變化0.05 GPa，室溫為20 ℃時，彈性模量為210 GPa。鋼軌溫度變化范圍為-20～60 ℃，為了避免估計應力時產生邊緣效應，將溫度的變化范圍擴大至-60～100 ℃，其等效的彈性模量變化范圍為206～214 GPa，每間隔2 GPa設置一個狀態點。溫度應力變化范圍是-100～100 MPa，每間隔20 MPa設置一個狀態點。除去彈性模量212 GPa狀態下，溫度應力值為-20、-40、-60、-80、-100 MPa的數據點(這些數據用于測試)，共有50種狀態數據。由于測試樣本不足，采用添加白噪聲形式獲得更多樣本，防止數據過度擬合。各模態時域信號引入5%的高斯白噪聲，彈性模量引入1%的高斯白噪聲，每一個狀態波數生成50個樣本，一共生成2 500組特征信號。

由于試驗條件的限制，目前尚不具備進行現場實物驗證的條件(這需要一段鎖定狀態下應力已知的鋼軌以及相應的相控陣采集處理系統)。因此，本文通過仿真獲取測量數據。測量數據的產生基于半解析有限元法建立的60 kg/m鋼軌模型。為了模擬現場實物試驗場景，本文使仿真測量的鋼軌模型與訓練標定函數時的鋼軌模型存在差異：設置參數時，彈性模量引入1%的高斯白噪聲；同時，傳感器采集的陣列信號存在隨機測量噪聲，時域信號引入5%的高斯白噪聲。這些差異和噪聲已達到實際應用可能存在的上限。

模型測量數據選取2種彈性模量和5種溫度應力狀態下的波數：在彈性模量210 GPa狀態下，選取溫度應力值10～90 MPa，每間隔20 MPa設置一個狀態點；在彈性模量212 GPa狀態下，選取溫度應力值-100～-20 MPa，每間隔20 MPa設置一個狀態點，共計10種狀態數據。每一個狀態生成50個樣本，共計500個測量樣本。模型預測應力誤差柱狀分布如圖8所示，總體估計應力誤差均值為0.210 1 MPa，標準差為0.726 4 MPa。圖9為10種狀態的應力估計誤差，由于每個狀態下應力估計標準差均小于1 MPa，圖形的縱坐標刻度為20 MPa，因此對應力估計的誤差線做放大20倍處理。圖9中最小的應力估計誤差是彈性模量210 GPa、拉應力10 MPa處，標準差為0.481 MPa；最大的應力估計誤差是彈性模量212 GPa、拉應力-40 MPa處，標準差為0.995 MPa。

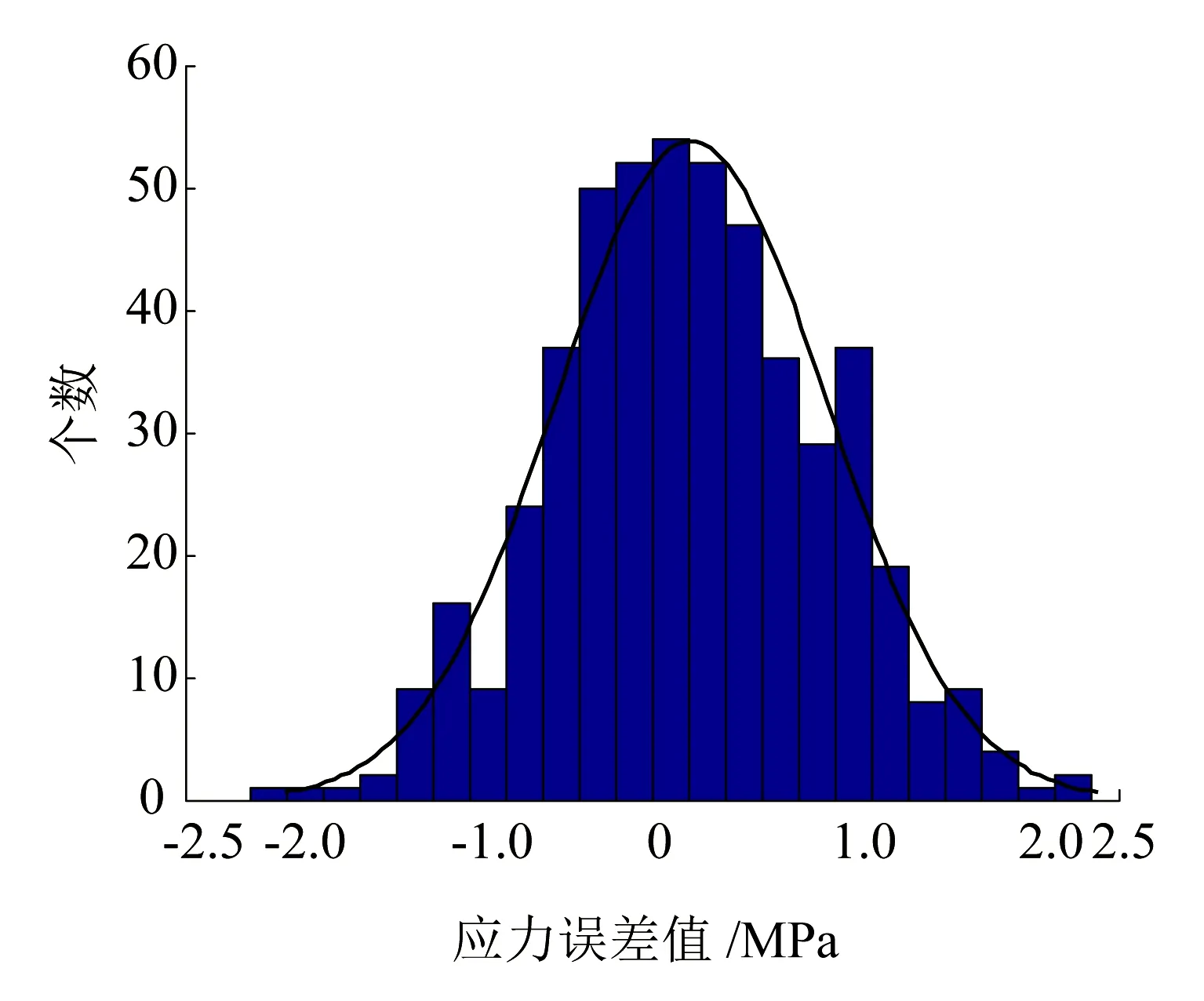
圖8 BP神經網絡預測應力誤差柱狀分布

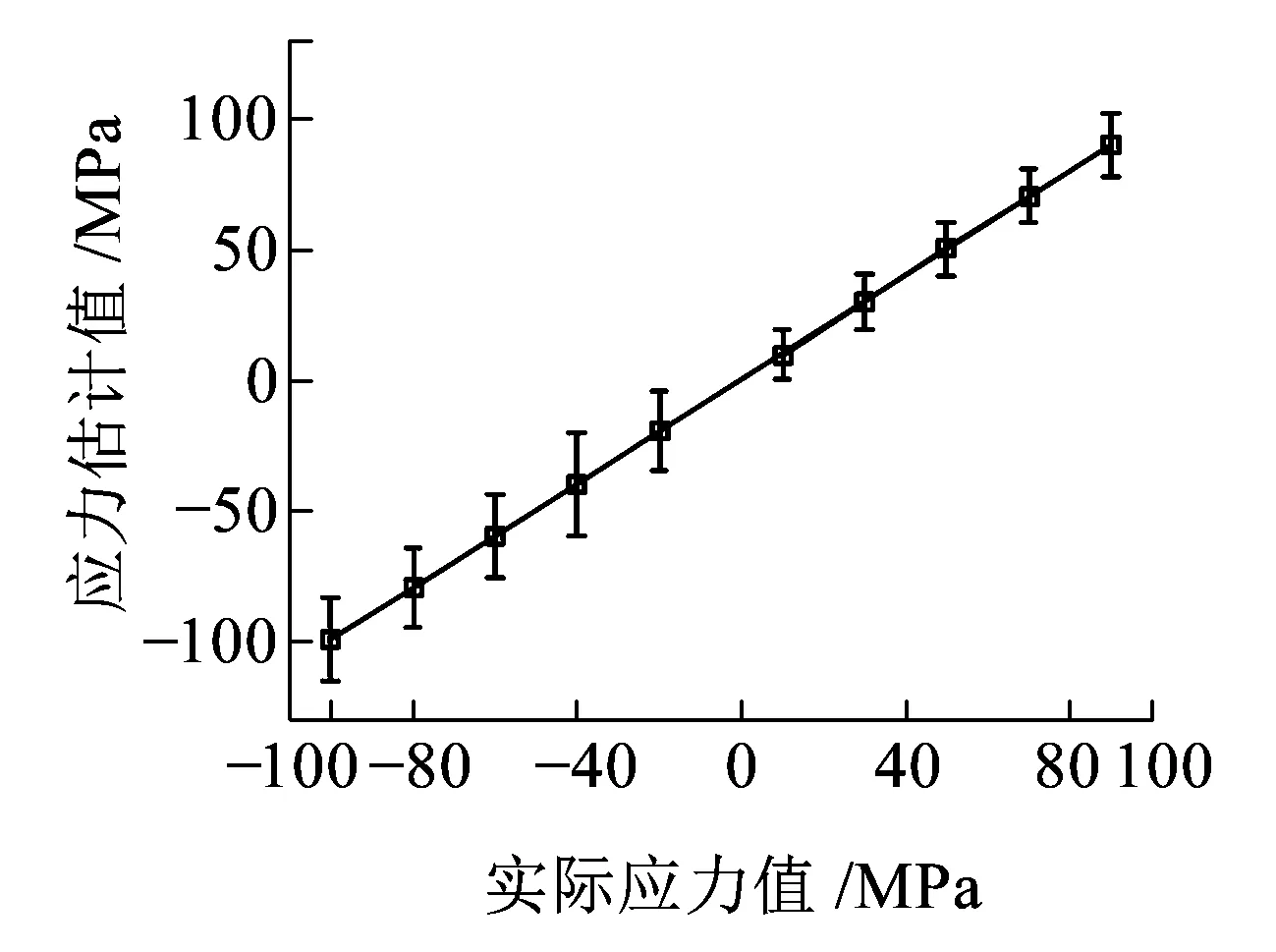
圖9 模型測量數據估計應力及標準差

4 結束語

無縫鋼軌縱向溫度應力的檢測與監測一直是一個技術難題，盡管近年來提出的超聲導波無損檢測原理得到了廣泛應用，但鋼軌彈性模量的不確定性制約著超聲導波檢測應力的測量精度。鋼軌彈性模量的不確定性一方面來源于溫度變化，另一方面來自不同批次鋼軌的差異性或者材料性能隨時間的衰變特性。本文基于鋼軌溫度應力檢測的誤差傳遞模型，分析波數、彈性模量與應力的影響關系，發現不同模態對應力和彈性模量的敏感度存在差異，提出利用多模態導波融合的彈性模型補償算法，實現彈性模量未知條件下鋼軌溫度應力的精確估計。仿真試驗結果表明，本文提出的多模態融合算法能夠克服彈性模量變化對溫度應力檢測的影響，為進一步研究無縫線路溫度應力的測量方法提供依據。

參考文獻：

[1]CHEN F,WILCOX P D.The Effect of Load on Guided Wave Propagation[J].Ultrasonics,2007,47(1/4):111-122.

[2]LOVEDAY P W.Semi-analytical Finite Element Analysis of Elastic Waveguides Subjected to Axial Loads[J].Ultrasonics,2009,49(3):298-300.

[3]劉增華,劉溯,吳斌,等.預應力鋼絞線中超聲導波聲彈性效應的試驗研究[J].機械工程學報,2010,46(2):22-27.

LIU Zenghua,LIU Su,WU Bin,et al.Experimental Research on Acoustoelastic Effect of Ultrasonic Guided Waves in Prestressing Steel Strand[J].Journal of Mechanical Engineering,2010,46(2):22-27.

[4]BARTOLI I,COCCIA S,PHILLIPS R,et al.Stress Dependence of Ultrasonic Guided Waves in Rails[C]//Proceedings of SPIE:The International Society for Optical Engineering,2010,7650:765021.

[5]許西寧,葉陽升,江成,等.鋼軌應力檢測中超聲導波模態選取方法研究[J].儀器儀表學報,2014,35(11):2473-2483.

XU Xining,YE Yangsheng,JIANG Cheng,et al.Research on Method for Mode Selection of Guided Ultrasonic Waves in Stress Measurement of Rails[J].Chinese Journal of Scientific Instrument,2014,35(11):2473-2483.

[6]LOVEDAY P W,WILCOX P D.Guided Wave Propagation as a Measure of Axial Loads in Rails[C]//Proceedings of SPIE:The International Society for Optical Engineering,2010,7650:765023.

[7]HAYASHI T,SONG W J,ROSE J L.Guided Wave Dispersion Curves for a Bar with an Arbitrary Cross-section,a Rod and Rail Example[J].Ultrasonics,2003,41(3):175-183.

[8]BARTOLI I,MARZANI A,LANZA D S F,et al.Modeling Wave Propagation in Damped Waveguides of Arbitrary Cross-section[J].Journal of Sound and Vibration,2006,295(3/5):685-707.

[9]盧耀榮.無縫線路研究與應用[M].2版.北京:中國鐵道出版社,2010:37-48.

[10]許西寧.基于超聲導波的無縫線路鋼軌應力在線監測技術應用基礎研究[D].北京:北京交通大學,2014.

[11]王嶸, 余祖俊,朱力強,等.基于導波速度的無縫鋼軌應力檢測方法[J].中國鐵道科學,2018,39(2):18-27.

WANG Rong,YU Zujun,ZHU Liqiang,et al.Detection Method for Stress in Continuously Welded Rail Based on Guided Wave Velocity[J].China Railway Science,2018,39(2):18-27.