基于改進非等間距灰色模型和PSVM的軌道質量指數預測

馬子驥，郭帥鋒，李元良

(湖南大學 電氣與信息工程學院，湖南 長沙 410082)

軌道不平順的形成受到多種因素的影響，包括軌道因素、載荷因素和自然因素等，這決定了軌道不平順是隨里程變化的隨機干擾函數[1]。國內外學者對軌道質量預測方法進行的研究工作基本分為兩類，一是將外界變量參數化構建出合適的模型。文獻[2]提出一種基于信號處理、統計和軌檢數據的綜合因子法，對軌道不平順發展趨勢進行了預測。文獻[3]從軌道構造條件、列車載荷對軌道及路基下沉量作用出發，通過軌道力學理論得到未來的軌道下沉量。二是構造合適的組合預測模型。文獻[4]利用線性預測模型預測軌道質量指數(TQI)的發展情況。文獻[5]利用實測軌道不平順歷史數據，通過回歸分析，得到軌道不平順的非線性預測公式。文獻[6]利用軌檢車動態檢測數據，提出一種基于不平順分布函數的不平順發展統計預測方法。文獻[7]利用軌道不平順TITCGM(1，1)-PC灰色非線性預測模型對TQI序列進行預測。為了充分反映軌道不平順的動態隨機性，文獻[8]提出基于非等時距灰色加權和BP神經網絡的軌道不平順預測方法，具有較高的預測精度。但是TQI序列屬于典型的小樣本貧信息不確定性系統，BP神經網絡受樣本容量影響較大，當樣本較少時對歷史數據的擬合較好，但是預測缺乏穩定性。

基于以上分析，本文充分利用支持向量機(SVM)[9]處理小樣本非線性高維數據的能力，提出一種基于非等間距GM(1，1)和粒子群優化[10]支持向量機(PSVM)的軌道不平順組合預測方法。將非等距序列變換為等間距累加均值序列，通過改進的灰色模型得到TQI的初步預測值，利用PSVM對灰色預測值進行修正，得到較精確的TQI序列。

1 改進的非等間距灰色模型

1.1 非等間距序列的變換

設非等間距TQI序列為

X(0)={x(0)(t1)，x(0)(t2)，…，x(0)(tn)}

將n個歷史數據X(0)轉換為等間距序列的步驟如下[11]：其對應的各觀測周期距首個周期的時間間隔為ti=Ti-T1，其中Ti為各期的原始觀測時間，且滿足

Δti=ti-ti-1≠consti=2，3，…，n

( 1 )

平均時間間隔為

( 2 )

各實際觀測時段與平均時間間隔的單位時段差系數為

( 3 )

各實際觀測時段的差值為

Δx(0)(ti)=u(ti)[x(0)(ti)-x(0)(ti-1)]

( 4 )

式中：x(0)(ti)為ti時刻的原始觀測值，i=2，3，…，n。Δx(0)(ti)=0。

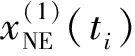
( 5 )

( 6 )

得到等間隔累加均值序列

( 7 )

1.2 GM(1，1)模型

由式( 7 )可知

X(1)={x(1)(t1)，x(1)(t2)，…，x(1)(tn)}

( 8 )

由一階生成序列x(1)(ti)構建GM(1，1)模型的白化形式，其微分方程為

( 9 )

式中：a為發展系數，用來控制系統發展態勢；u為灰色作用量，用來反映數據變化的不確切關系。

將式( 9 )在區間[ti-1，ti]上積分

(10)

可得離散化差分方程為

x(0)(ti)Δti+az(1)(ti)=uΔti

(11)

式中：z(1)(ti)為x(1)(ti)在區間[ti-1，ti]上的背景值。

利用最小二乘法求得待辨識參數a、u，即

[au]T=(BTB)-1BTG

(12)

其中

(13)

將a、u代入式(10)中可得時間響應函數

(14)

式中：i=2，3，…，n。

GM(1，1)模型預測值為

(15)

如果在級數比檢驗時進行平移，需將式(15)等號右邊減去常數c，c為使原始數據序列的級數比都落在可容覆蓋范圍內的常數。

1.3 GM(1，1)模型優化

GM(1，1)模型的模擬預測精度取決于參數a、u，a、u的值又取決于z(1)(ti)的求解，因此背景值是影響灰色理論建模精度的重要因素之一。傳統GM(1，1)模型把序列x(1)(ti)在區間上的連續函數視為直線，用梯形公式近似代替區間[ti-1，ti]上累加曲線x(1)(ti)與t軸圍成的面積。文獻[8，12]指出使用齊次指數擬合灰指數序列對其積分，并將積分值作為背景值，但是一階累加生成序列并不一定都是齊次序列。因此本文利用一種復化梯形公式[13]解決更為一般的1-AGO序列，從積分幾何意義出發，利用函數逼近思想，得到更精確的GM(1，1)背景值。由文獻[13]可知，一階累加序列可表示為一般的非齊次序列

x(1)(ti)=Aeαti-1+B

(16)

式中：

B=x(0)(t1)-A

式(11)中的z(1)(ti)可以表示為

(17)

式中：k表示將區間[ti-1，ti]均分為k段。

2 PSVM修正預測模型

2.1 支持向量機

支持向量機(SVM)是由Vapnik等根據統計學習理論中結構風險最小化(SRM)原則提出的，具有良好的泛化能力。SVM既有嚴格的理論基礎，又能較好地處理小樣本非線性高維數問題，能夠避免陷入局部極小值。利用支持向量機可以將輸入樣本向量通過事先選擇的非線性映射變換到高維特征空間，并在這個高維空間中得到自變量和因變量之間的非線性映射關系。

支持向量機函數擬合問題就是用函數f(x)=wx+b擬合數據(xi，yi)，i=1，2，…，n，xi∈Rn，yi∈Rn。數據樣本為n組數據，即n維向量。支持向量機擬合函數為

(18)

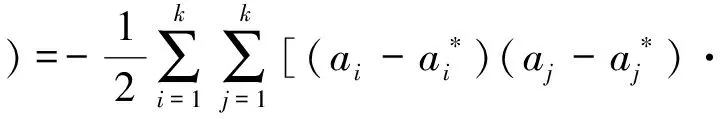
使得

(19)

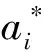
對于非線性問題，若在原樣本空間中不能得到滿意結果，可以通過非線性變換轉化為某個高維空間中的線性問題，在變換空間求得最優分類面。這種變換可能比較復雜，SVM通過引入核函數成功解決了這一問題。高維計算的核函數主要有多項式核函數、徑向基核函數(RBF)和Sigmoid核函數。

2.2 PSVM修正預測模型

由于單一灰色模型可能存在較大的偏差，所以本文利用SVM對GM(1，1)模型預測的軌道不平順TQI值進行修正預測。研究表明，懲罰參數C與核函數參數g是影響SVM性能的關鍵參數，目前還沒有合適的理論能夠指導參數選擇[14]。因此，使用粒子群優化算法對SVM的懲罰參數C、核函數參數g進行選擇，可以有效避免參數選擇不當對SVM的影響。PSO算法是一種經典的群智能算法，其粒子尋優基本過程為

vij(t+1)=wvij(t)+c1×r1×

[pij-xij(t)]+c2×r2[pgi-xij(t)]

(20)

xij(t+1)=xij(t)+vij(t+1)

(21)

式中：w為慣性因子；r1、r2為(0，1)區間服從均勻分布的隨機數；c1、c2為學習因子，其個體極值為pbest，pi=(pi1，pi2，…，pid)，i=1，2，…，n；n為粒子數，d為粒子維度；全局最優解為gbest，表示所有粒子的全局極值所在位置，pg=(pg1，pg2，…，pgn)。

3 本文預測步驟

基于以上理論分析，本文設計的TQI預測方法為：對原始TQI數據進行級數比檢驗，判斷是否需要平移變換；利用改進的非等間距灰色模型對TQI值進行初步預測，利用復化梯形公式對該模型進行背景值優化；將得到的初步預測值輸入PSVM模型中進行修正預測，得到本文組合模型的最終預測值。灰色和PSVM模型結構如圖1所示。

圖1 灰色和PSVM模型結構

具體計算步驟如下：

步驟1對原始數據序列進行級數比檢驗，如果不符合要求，則將數據進行平移處理。

計算其級數比為

(22)

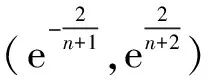
X(0)=X(0)+c

(23)

步驟2將處理過的非等間距TQI序列X(0)進行變換處理，得到等間隔的一階累加均值序列X(1)，如式( 7 )所示。

步驟3在每個時間間隔[ti-1，ti]內插入3個點將其均分為4份，利用復化梯形公式對GM(1，1)模型的背景值z(1)(ti)進行優化。

步驟4利用最小二乘法估計灰色模型的參數a、u，得到最終灰色模型預測的時間響應函數。

步驟5利用步驟4得到基于灰色模型預測的原始TQI數據為

(24)

步驟6將灰色模型預測得到的原始TQI數據Pg作為PSVM修正模型的輸入，TQI真實值X(0)作為其輸出，對模型進行訓練，得到最優化C、g的PSVM模型。具體方法為：通過對學習因子c1、c2和權重系數進行初始化，初始化粒子的位置和速度，每個粒子設置為初始最好位置；計算每個粒子的適應度，粒子的適應度采用K折交叉檢驗進行評估，根據式(19)更新粒子的速度和位置；最后判斷是否滿足終止條件，若滿足，則將群體中最優粒子映射為SVM懲罰參數C和核函數參數g最優解，否則，返回步驟2開始下一次搜索。

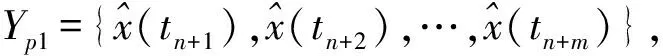
4 計算驗證

以文獻[7]中提速干線滬昆線上行K226.4～K226.6和K226.8～K227的TQI檢測數據為例。將2007年9月—2008年8月一年內的19個數據作為穩定維修周期內積累的原始數據，對2008年9月—2008年12月的7個TQI數據進行預測。支持向量機采用林智任編寫的libsvm包，用PSO算法優化SVM的徑向基核函數，其表達式為

K(x，xi)=exp[-‖x-xi‖2/(2σ2)]

(25)

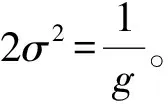
相對誤差

(26)

平均誤差

(27)

4.1 K226.4～K226.6區間段分析

讀取滬昆線上行K226.4～K226.6的19個訓練樣本數據，PSO優化SVM模型參數過程中的均方誤差適應度隨迭代次數的變化曲線如圖2所示。迭代結束時，搜索得到的SVM懲罰參數C=100，核函數參數g=1.187 6，CVmse=0.245 12。

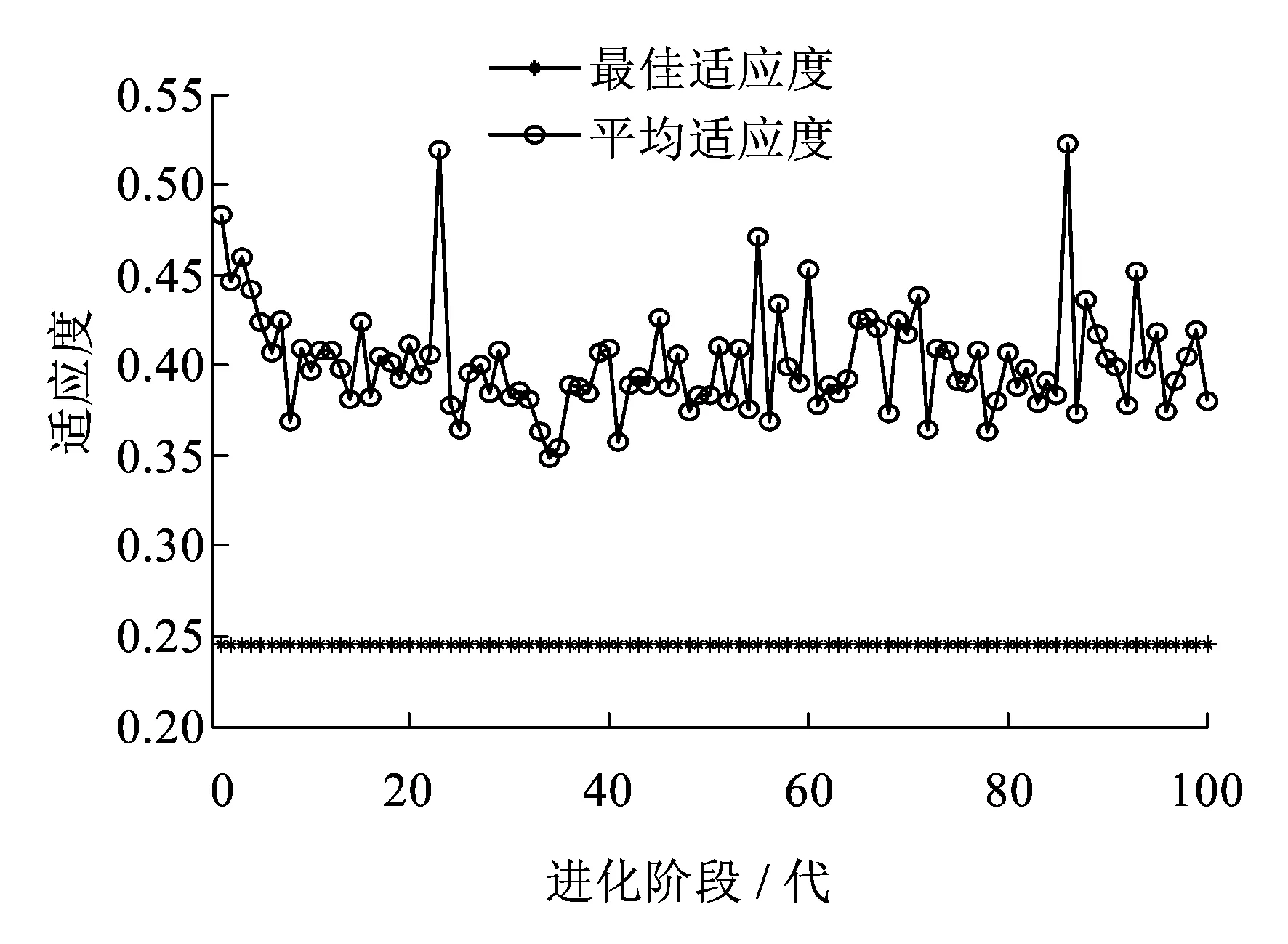
圖2 PSO優化SVM參數的適應度曲線

利用改進的非等間距灰色模型預測結果如圖3所示，利用PSVM模型進行修正的結果如圖4所示。由圖3可看出，灰色模型的預測大致反映了TQI序列的變化方向，誤差較大。由圖4可看出，雖然經過PSVM模型進一步糾正之后訓練結果對歷史數據擬合效果一般，但SVM小樣本學習和良好的外推能力使預測誤差明顯減小。本文預測模型與文獻[7]的TITCGM(1，1)-PC模型和文獻[8]的灰色與神經網絡組合預測模型對比結果見表1。顯然，文獻[7]模型個別誤差過大，最大為12.64%；文獻[8]灰色與神經網絡組合預測模型由于神經網絡權值和閾值是運行時隨機賦值的，具有不確定性且訓練性能依賴大樣本數據，訓練結果雖然對歷史數據擬合較好，但是預測性能欠佳。

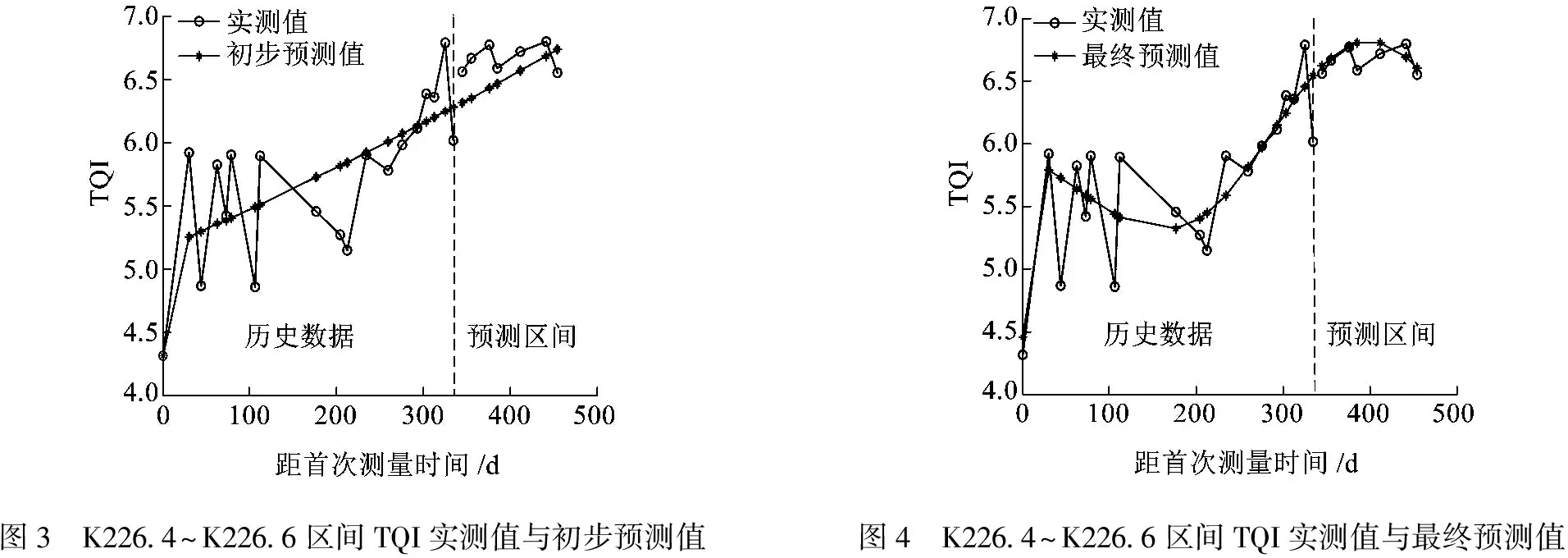
圖3 K226.4～K226.6區間TQI實測值與初步預測值圖4 K226.4～K226.6區間TQI實測值與最終預測值

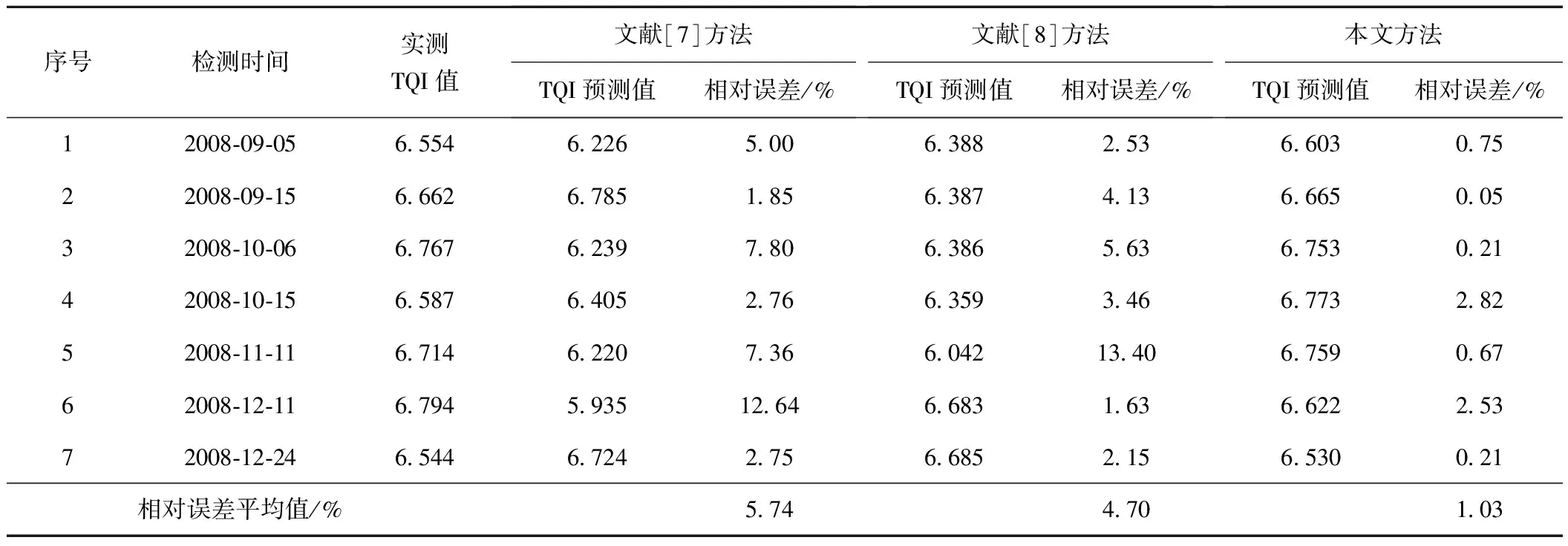
表1 K226.4～K226.6區間內3種算法的TQI預測結果比較

4.2 K226.8～K227區間段分析

為了避免連續區段TQI變化較接近，另取滬昆線上行K226.8～K227的19個訓練樣本數據，PSO優化SVM模型參數過程中的均方誤差適應度隨迭代次數的變化曲線如圖5所示。當迭代結束時，搜索得到的SVM懲罰參數C=261.700 9，核函數參數g=1.406 9，CVmse=0.098 162。

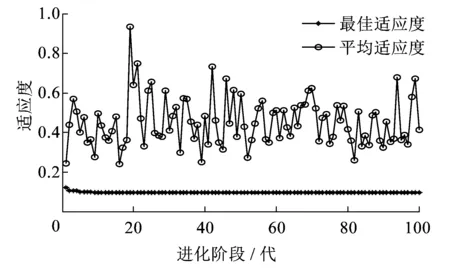
圖5 PSO訓練SVM參數的適應度曲線

利用改進的非等間距灰色模型預測結果如圖6所示，利用PSVM模型進行修正的結果如圖7所示。由圖6可以看出，灰色模型的預測誤差較大。經過PSVM模型進一步糾正之后訓練結果對歷史數據的擬合效果一般，但預測誤差較小，結果如圖7所示。本文預測模型與文獻[7]中的TITCGM(1，1)-PC模型和文獻[8]的灰色與神經網絡組合預測模型對比結果見表2。

圖6 K226.8～K227區間TQI實測值與初步預測值

序號檢測時間實測TQI值文獻[7]方法TQI預測值相對誤差/%文獻[8]方法TQI預測值相對誤差/%本文方法TQI預測值相對誤差/%12008-09-056.7936.5493.596.4574.956.3596.3922008-09-156.5026.6412.146.4590.666.4251.1832008-10-066.6666.3944.086.4563.156.5701.4442008-10-156.6236.2805.186.4562.526.6330.1552008-11-116.9707.1342.356.4617.306.8232.1162008-12-116.6577.53713.226.5251.987.0285.5772008-12-247.2847.6444.947.0073.807.1122.36相對誤差平均值/%5.073.482.74

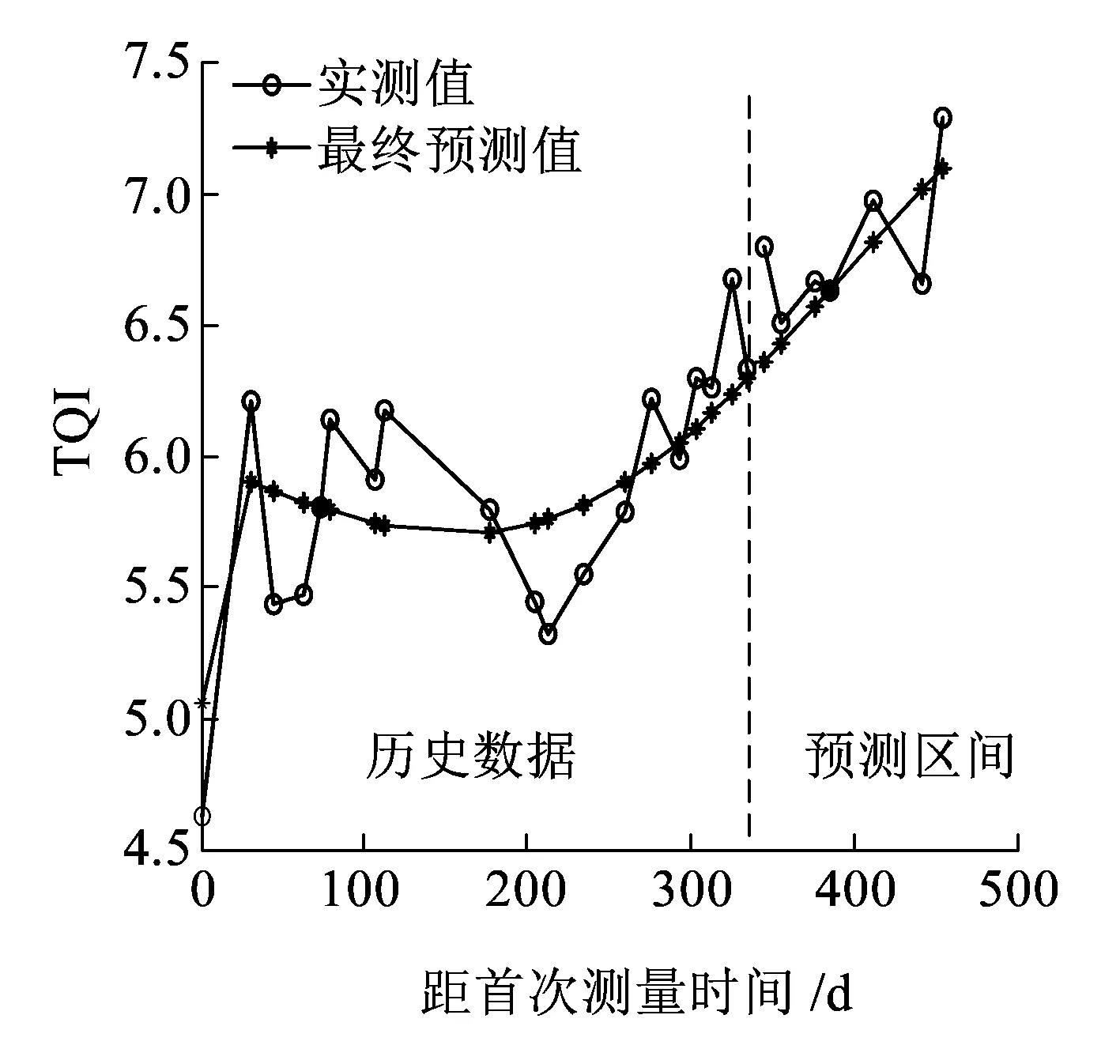
圖7 K226.8～K227區間TQI實測值與最終預測值

5 結論

(1)計算TQI累計序列微分方程的背景值時，從積分的幾何意義出發，利用函數逼近思想，通過復化梯形公式構造背景值，提高預測精度。

(2)隨著預測時間的延長，灰色模型在實際應用中預測精度會降低，在實踐中應當對模型不斷試驗，總結出對多長時間內進行預測既可以減少運算量又滿足精度要求。

(3)利用PSO算法的全局搜索能力，將SVM的懲罰參數C和核函數參數g作為粒子向量進行全局尋優，該方法克服了SVM對參數敏感的缺點，避免了根據經驗確定模型參數導致的不確定性。

(4)PSVM模型中的不敏感損失函數應隨著預測區段的不同進行微調，訓練樣本也應及時補充完善，提高預測精度。

(5)TQI序列屬于典型的小樣本貧信息不確定性序列。利用支持向量機對TQI灰色預測值進一步修正，可充分發揮其良好的預測性能和泛化能力，克服了單一灰色預測模型的不足，具有較高的使用價值。

正確預測軌道質量指數的變化對提高軌道平順性意義重大，本文以滬昆線上行兩段線路的預測分析為例，采用灰色模型和粒子群優化的支持向量機組合模型探討解決這一問題的方法，并與實測值進行比較，取得了較理想的效果，預測相對誤差低于現有的TITIGM-PC模型和灰色神經網絡組合預測模型。

參考文獻：

[1]羅林.軌道隨機干擾函數[J].中國鐵道科學,1982,3(1):74-112.

LUO Lin.Track Random Excitation Function[J].China Railway Science,1982,3(1):74-112.

[2]陳憲麥.軌道不平順時頻域分析及預測方法的研究[D].北京:鐵道部科學研究院,2006.

[3]三和雅史,內田雅夫.軌道狀態推移モデルの設定と軌道保守施策決定法[J].鉄道総研報告,1996(4):7-12.

[4]許玉德,吳紀才.利用線性預測模型分析軌道不平順發展[J].石家莊鐵道學院學報,2005,18(1):6-9.

XU Yude,WU Jicai.Analysis on Development of Track Irregularities with Linear Forecast Model[J].Journal of Shijiazhuang Railway Institute,2005,18(1):6-9.

[5]杉山徳平,家田仁,上野昌喜.軌道狂い狀態を考慮した軌道破壊の要因分析[J].鉄道線路,1986,34(9):442-446.

[6]高建敏,翟婉明,徐涌,等.基于概率分布的軌道不平順發展統計預測[J].鐵道科學與工程學報,2006,3(6):55-60.

GAO Jianmin,ZHAI Wanming,XU Yong,et al.Development Forecast Model of Track Irregularity Based on Probability Distribution[J].Journal of Railway Science and Engineering,2006,3(6):55-60.

[7]曲建軍.基于提速線路TQI 的軌道不平順預測與輔助決策技術的研究[D].北京:北京交通大學,2011.

[8]韓晉,楊岳,陳峰,等.基于非等時距加權灰色模型與神經網絡的軌道不平順預測[J].鐵道學報,2014,36(1):81-87.

HAN Jin,YANG Yue,CHEN Feng,et al.Prediction of Track Irregularity Based on Non-equal Interval Weighted Grey Model and Neural Network[J].Journal of the China Railway Society,2014,36(1):81-87.

[9]VAPNIK V N.Statistical Learning Theory[M].New York:Wiley,1998.

[10]XUE Z H,DU P J,SU H J.Harmonic Analysis for Hyperspectral Image Classification Integrated with PSO Optimized SVM[J].IEEE Journal of Selected Topics inApplied Earth Observations and Remote Sensing,2014,7(6):2131-2146.

[11]李斌,朱健.非等間隔灰色GM (1,1) 模型在沉降數據分析中的應用[J].測繪科學,2007,32(4):52-55.

LI Bin,ZHU Jian.Application of Unequal Interval Grey Model in Analysis of Settlement Data[J].Science of Surveying and Mapping,2007,32(4):52-55.

[12]曲建軍,高亮,辛濤,等.基于改進灰色-馬爾可夫鏈的軌道不平順發展預測方法[J].北京交通大學學報,2010,34(4):107-111.

QU Jianjun,GAO Liang,XIN Tao,et al.Track Irregularity Development Prediction Method Based on Grey-Markov Chain Model[J].Journal of Beijing Jiaotong University,2010,34(4):107-111.

[13]蔣詩泉,劉思峰,周興才.基于復化梯形公式的GM(1,1)模型背景值的優化[J].控制與決策,2014,29(12):2221-2225.

JIANG Shiquan,LIU Sifeng,ZHOU Xingcai.Optimization of Background Value in GM(1,1) Based on Compound Trapezoid Formula[J].Control and Decision,2014,29(12):2221-2225.

[14]王生生,楊娟娟,柴勝.基于混沌鯰魚效應的人工蜂群算法及應用[J].電子學報,2014,42(9):1731-1737.

WANG Shengsheng,YANG Juanjuan,CHAI Sheng.Artificial Bee Colony Algorithm with Chaotic Catfish Effect and Its Application[J].Acta Electronica Sinica,2014,42(9):1731-1737.