基于彈復力效應的列控車載設備可靠性分析方法
上官偉,胡福威,袁 敏,蔡伯根,3,王 劍
(1.北京交通大學 電子信息工程學院,北京 100044;2.北京交通大學 軌道交通控制與安全國家重點實驗室,北京 100044;3.北京市電磁兼容與衛星導航工程技術研究中心,北京 100044)
高速鐵路系統作為我國綜合運輸網絡中的重要組成部分,該系統能否正常運行關系著乘客的生命及財產安全。排除人為因素、自然環境影響以外,由于系統本身不可避免地存在一些安全隱患,所以當列車在極端惡劣的條件下運行時,可能會導致一些重大事故發生。因此,為了確保列車安全、可靠的運行,針對列車運行過程中的可靠性分析方法以及故障恢復策略的研究,對于杜絕和減少重大鐵路行車安全事故的發生具有重要的現實意義。
列車運行控制系統(以下簡稱列控系統)是保證我國高速鐵路系統安全運行的核心設備之一,由于系統自身具有復雜性和不確定性等特點,所以在運行時對其內部運行狀態及外界環境的變化都具有較強的敏感性。因此,在行車時應及時診斷出系統中出現的故障或安全漏洞,并對其加以處理,否則將有可能引發一系列的設備單元故障,甚至造成重大的經濟損失和人員傷亡。極端條件下,列車在運行過程中因受到某些干擾而造成設備的故障依舊不可避免,所以如何對系統的運行可靠性進行實時分析是研究的一個難點。針對列控系統的可靠性分析,國內外的一些專家學者已經采用了很多較為成熟的理論方法進行研究,但仍有一些不足之處。
彈復力的概念來源于物理學領域,其物理特性參照彈簧因彈性形變所儲存的彈性勢能。當前彈復力的研究工作已經逐步成為分析和評估交通系統可靠性和安全性的一個重要方面。文獻[1]對運輸系統的彈復能力進行分析,并確定了系統的彈性參數及關鍵變量,以確定系統在動態環境中受到損害時的恢復能力。文獻[2]提出了一個用于計算社區災后恢復能力的概念框架,該框架提升社區彈復能力的依據是降低故障率、減少故障損失以及降低復原時間。文獻[3]認為系統的彈復力工程表示了一種新的安全思維方式,與傳統的風險評估方法不同,彈復力可用于評估系統應對風險的能力。文獻[4]根據常規的風險管理方法并結合彈復力的概念,重新對不確定性、脆弱性和風險等概念進行了定義。文獻[5]將研究對象映射到一個網絡中,并附加線性方法的約束,通過關鍵路徑算法對網絡中的路徑結構加以調整,最終實現對系統彈復力大小的評估。對比傳統的可靠性評估方法,彈復力將系統在運行時對外部環境刺激的響應以及系統內部單元模塊之間的信息交互考慮在內,可以比較全面地分析大型復雜系統在功能失效過程中的性能變化。
本文以CTCS3-300H型車載設備為研究對象,引入了彈復力的概念,結合歷史故障數據,選用離散時間貝葉斯網絡DTBN(Discrete Time Bayesian Network)方法,對車載設備在運行過程中的可靠性進行定量分析,計算出車載設備在不同工作模式下隨著工作時間的增加,車載設備可靠度的變化情況;基于車載設備在運行過程中的可靠度結果,依據彈性三角模型,假設車載設備在某個時刻發生故障時,對系統的彈復能力進行評估;根據分析結果提出了基于彈復力效應的視情維修策略,從而提高系統在運行過程中的可靠性。CTCS3-300H型車載設備的結構組成示意圖如圖1所示[6]。
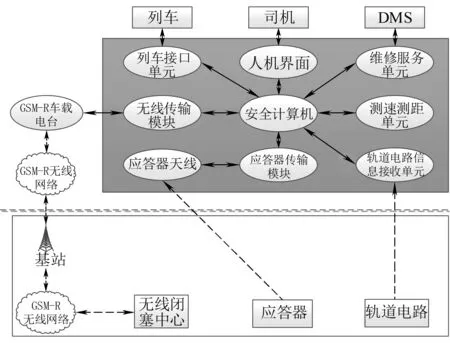
圖1 CTCS3-300H型車載設備組成
其中,應答器傳輸模塊BTM(Balise Transmission Module)通過與應答器天線的連接,可以完成地面應答器報文信息的接收;安全計算機VC(Vital Computer)根據與地面系統交換的信息,生成實時運行控制曲線;無線傳輸模塊RTM(Radio Transmission Module)、車載電臺和GSM-R實現車載與地面連續且雙向的信息通信;繼電器邏輯單元RLU(Relay Logic Unit)用于輸出車載設備的控制命令,同時將采集到的繼電器信息傳輸給安全計算機;人機界面DMI(Driver Machine Interface Unit)一方面對司機輸出操作列車的相關信息,另一方面司機可通過人機界面輸入相關的操作命令,從而實現車載設備與列車司機之間的信息交互;軌道電路信息接收單元TCR(Track Circuit Reader Unit)通過與軌道電路接收天線連接,接收軌道電路傳輸的信息并對其進行解碼。
車載設備中的測速測距單元SDU(Speed Distance Unit)、VC、DMI、TCR、BTM等模塊都采用冗余設計,其中,SDU設計為二取二結構,VC和TCR采用雙系熱備的配置方式,BTM和DMI則采用雙系冷備的配置方式。除此之外,還包含司法記錄單元JRU(Juridical Recording Unit)等其他模塊單元。
1 基于貝葉斯網絡的車載設備可靠性分析
1.1 離散時間貝葉斯網絡方法
以貝葉斯網絡BN(Bayesian Network)為基礎,引入時間參數,得到離散時間貝葉斯網絡方法,該方法可以有效地對動態失效和順序失效等網絡問題進行處理。具有N個節點的DTBN可用N=〈〈V,Tn,E〉,P〉來表示。DTBN為一個有向無環圖,該網絡的邊和變量的表示方式與含義和BN相同。DTBN算法中引入的時間特性Tn={[t0,t1),…,[ti-1,ti),…,[tn-1,tn),[tn,∞)}是針對時間的一個分割,分割的每一個區間表示變量發生時所處的時間段;DTBN中節點的狀態空間都是Tn,即模塊或系統的失效是發生在Tn中某一個時間區間內[7]。為了確定離散時間貝葉斯網絡中各節點的條件概率分布,需要明確節點之間的邏輯關系。
(1)單節點
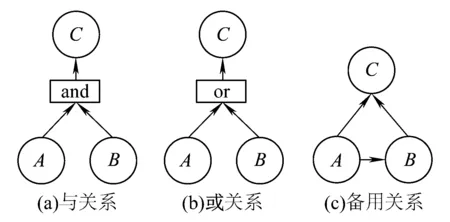
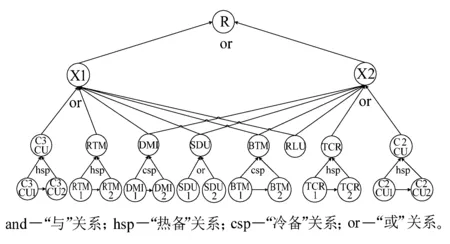
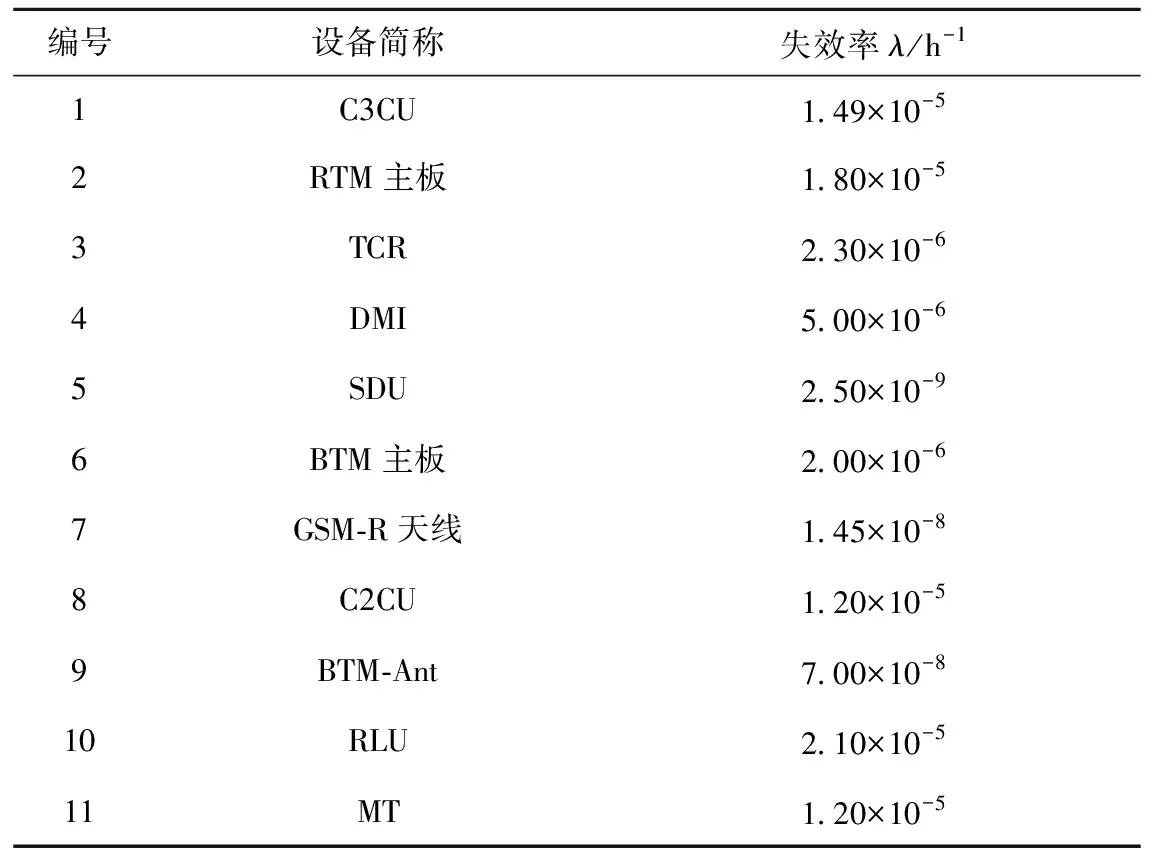
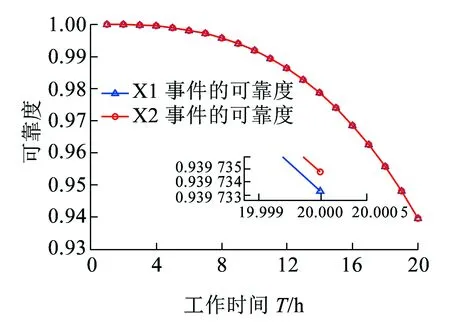
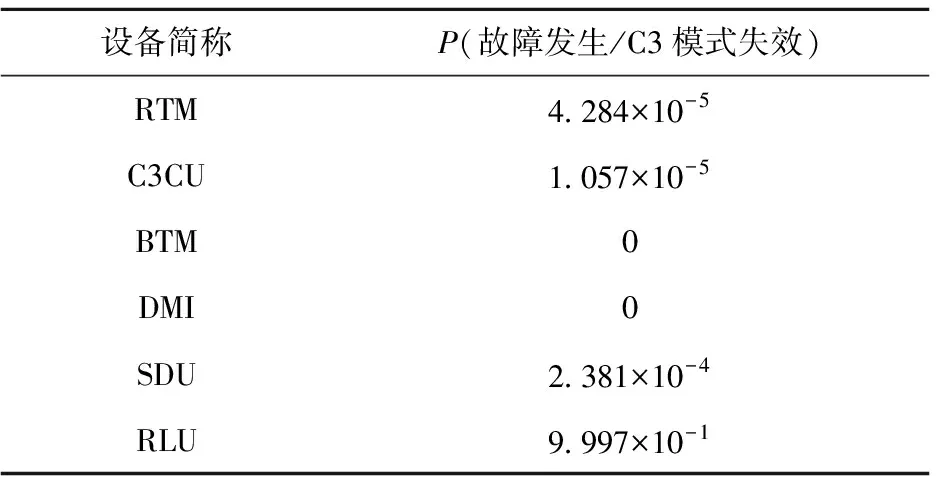
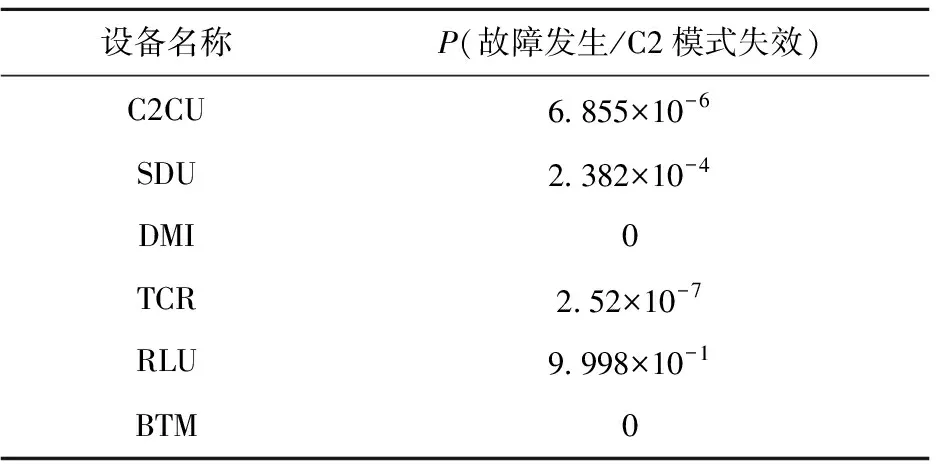
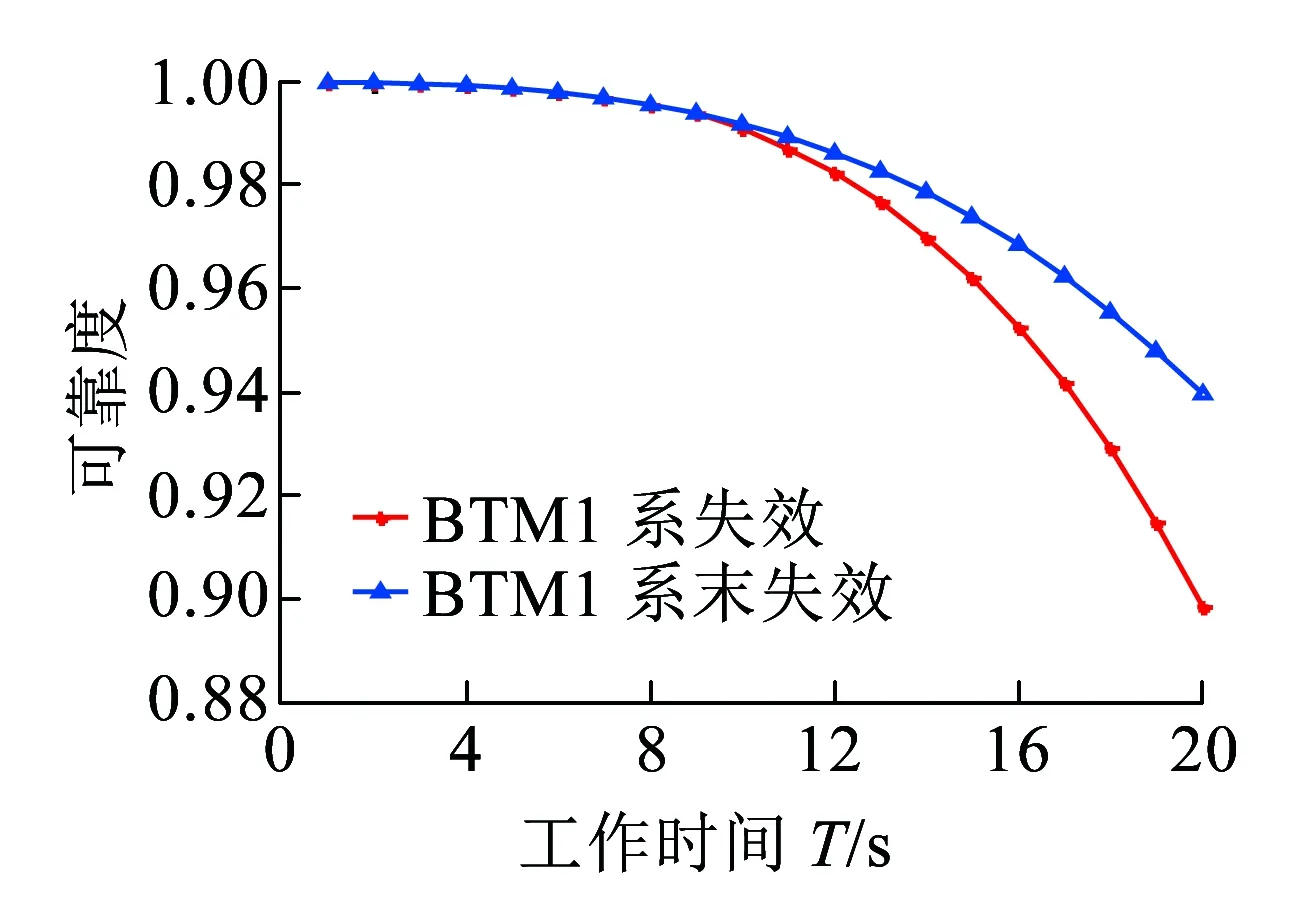
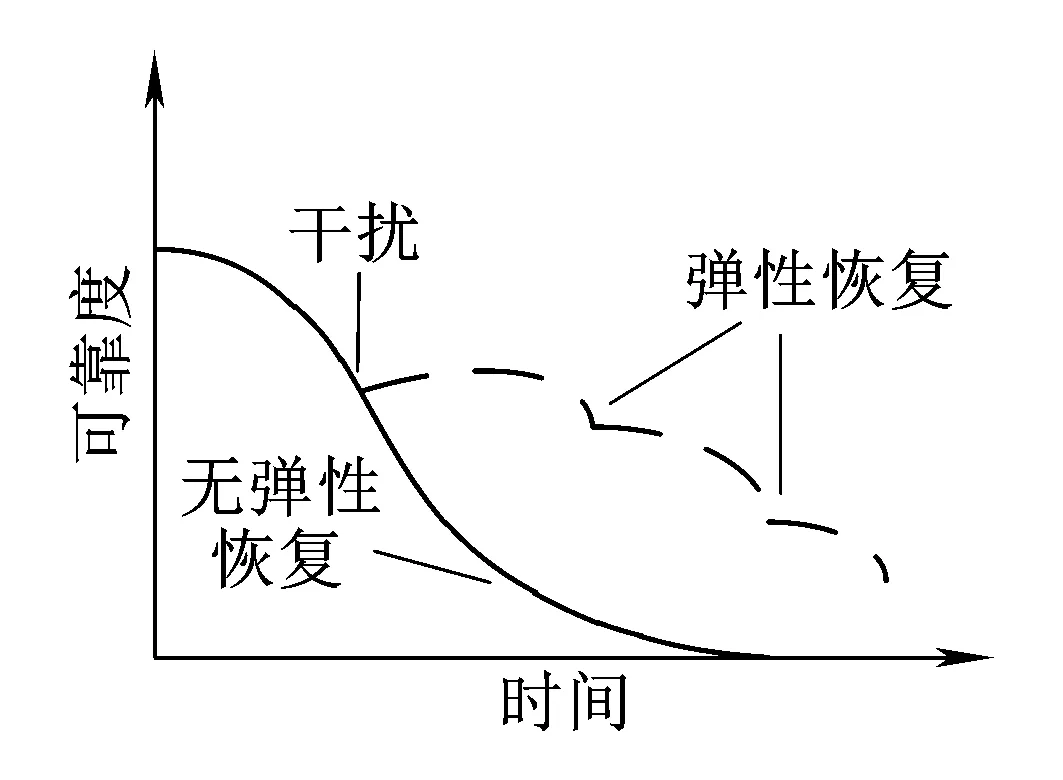
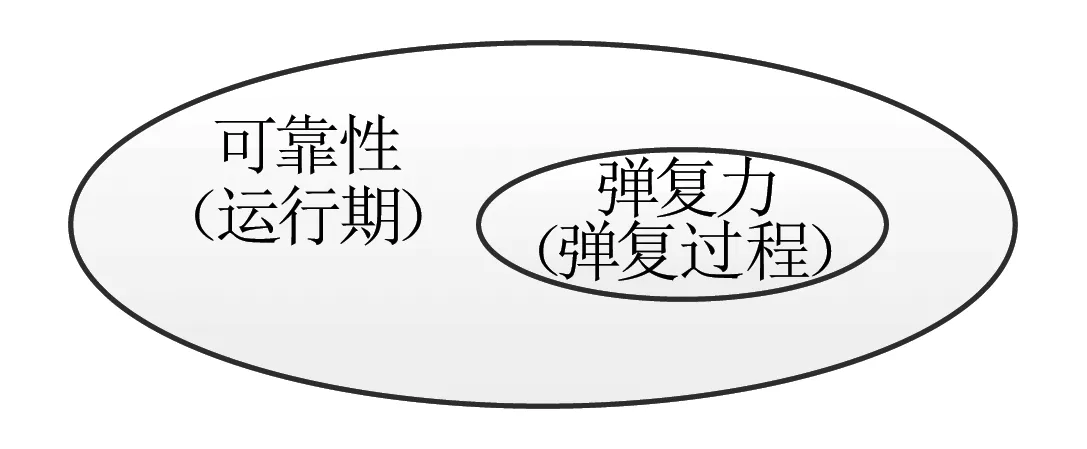
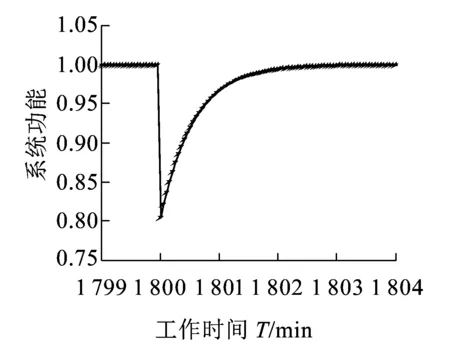
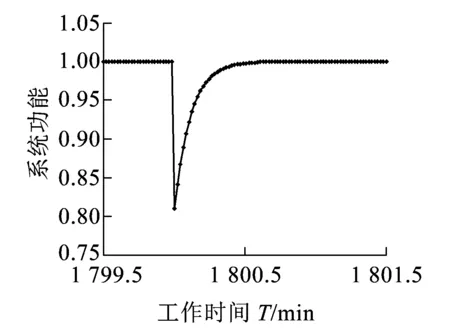
若系統的運行時間為T,將時間T分割為n個區間,則區間的大小為Δ=T/n。X=[(x-1)Δ,xΔ)表示X在[(x-1)Δ,xΔ)內失效,其中0 0 ( 1 ) ( 2 ) (2)“與”關系 兩個節點之間若存在“與”的關系,則使用“and”連接兩節點,相應的DTBN如圖2(a)所示(本節中的示例均假設n=2)。 圖2 離散時間貝葉斯網絡中節點的邏輯關系 其中節點C的條件概率分布為 Px,y,z=P(C=[(z-1)Δ,zΔ)|A= [x-1)Δ,xΔ),B=[y-1)Δ,yΔ))= ( 3 ) (3)“或”關系 兩個節點之間若存在“或”的關系,則使用“or”連接兩個節點,相應的DTBN如圖2(b)所示,節點C的條件概率分布可表示為 Px,y,z=P(C=[(z-1)Δ,zΔ)|A= [(x-1)Δ,xΔ),B=[(y-1)Δ,yΔ))= ( 4 ) (4)“備用”關系 備用是指系統中某一單元包含多個相同的部件,其中一個為主部件,其余的為備用部件,且同一時刻保障系統的正常運行部件只有一個。當主部件在工作過程中發生失效時,系統自動或人工切換至一個備用部件,若第一個備用部件此時也發生失效,則切換至第二個備用部件,直至該單元所有部件都失效,則單元失效[8]。 休眠因子α被定義為部件備用時的失效率與工作時的失效率之比,備用部件可分為冷備(α=0)、溫備(0<α<1)和熱備(α=1)三種類型。以溫備為例,“備用”關系所構建的DTBN如圖2(c)所示。假設主部件A和備用部件B的失效率都是λ,B的休眠因子為α(0<α<1),則B的條件概率分布為 Px,y=P(B=[(y-1)Δ,yΔ)|A=[(x-1)Δ,xΔ))= ( 5 ) Px,∞=P(B=[T,∞)|A=[(x-1)Δ,xΔ))= ( 6 ) P∞,y=P(B=[(y-1)Δ,yΔ)|A=[T,∞))= ( 7 ) P∞,∞=P(B=[T,∞)|A=[T,∞))= ( 8 ) Px,y,z=P(C=[(z-1)Δ,zΔ)|A= [(x-1)Δ,xΔ),B=[(y-1)Δ,yΔ))= ( 9 ) 除了前面所描述的4種節點之間的邏輯關系,還存在其他的邏輯關系[9]。在確定網絡中各個節點之間的關系后,依據相關歷史數據和專家經驗,得到節點的條件概率分布;之后,通過輸入對應的先驗信息來實現對時序系統相關概率的評估與分析。在構建離散時間貝葉斯網絡之后,通過輸入節點的先驗概率分布和聯合概率分布,可以計算出各個結果在時間區間T內發生的概率。 列車在正常運行過程中,車載設備有兩種控車模式:C3控制模式(X1)和C2控制模式(X2)。通過對CTCS-300H型車載設備結構和工作原理的深入分析,構建車載設備在兩種工作模式下的DTBN,如圖3所示。其中貝葉斯網絡中的符號含義見表1。 圖3 基于不同模式下的DTBN 符號含義符號含義R車載設備故障RLU繼電器邏輯單元X1C3模式故障X2C2模式故障TCR1軌道電路信息接收單元1系TCR2軌道電路信息接收單元2系RTM1無線傳輸模塊1系RTM2無線傳輸模塊2系SDU1測速測距單元1系SDU2測速測距單元2系BTM1應答器傳輸模塊1系BTM2應答器傳輸模塊2系C3CU1CTCS-3控制單元1系C3CU2CTCS-3控制單元2系DMI1人機界面1系DMI1人機界面2系C2CU1CTCS-2控制單元1系C2CU2CTCS-2控制單元2系 無線傳輸模塊包括RTM主板、GSM-R天線和車載無線電臺;應答器傳輸模塊則包括BTM主板和BTM天線。 假設模塊的硬件故障概率分布符合指數分布,則失效率λ[10-13]見表2。 表2 車載設備子模塊的故障率 在20 h內進行貝葉斯網絡正向推理得到不同工作模式下車載設備的可靠度變化曲線如圖4所示。 圖4 T=20 h的事件X1和X2的可靠度比較 隨著工作運行時間的增加,事件X1和事件X2的可靠性逐漸下降,兩個事件的可靠度曲線變化相似,但實際上兩者在各個時間點的可靠度卻不相同。通過仿真結果可以發現,設備在運行20 h后X1的可靠度開始小于X2,即車載設備在C3狀態下運行的可靠度下降速度大于在C2狀態下的下降速度。 假設車載設備的可靠性下降到一定程度時,采用貝葉斯網絡的反向推理特性,推導出當整個系統失效時各個單元模塊故障的概率,參照故障率的大小,為車載設備制定后續維修策略提供參考依據。 在C3模式下,若車載設備發生失效,則各個單元發生故障的概率見表3。 表3 C3級模式失效情況下各個模塊單元的故障概率 根據表3可知,當車載設備失效時,RLU模塊故障的可能性最大,因此在后續過程中,應加強對RLU的檢修;然后依次是SDU、RTM、C3CU。DMI和BTM是雙系冷備結構,即當模塊的1系發生失效時,系統可切換至2系工作,因此整個模塊可以正常工作。 同理,若車載設備運行在C2模式下時,則各個子模塊可能失效的概率見表4。 表4 C2級模式失效情況下各個模塊單元的故障概率 根據表4可知,車載設備在C2模式下,RLU失效的可能性最高,其次是SDU。 綜上所述,從車載設備失效的角度出發,各個單元模塊的重要度排序:RLU、SDU、RTM、C3CU、C2CU、TCR、BTM、DMI。所以在日常檢測過程中應加強對RLU、SDU等模塊的檢測。 建立基于模塊失效的車載設備DTBN如圖5所示,其中E表示車載設備。 圖5 基于模塊失效的DTBN 車載設備的很多硬件模塊采用了冗余結構,當設備的1系發生故障時,通過倒系的手段切換到2系,以保證系統的正常運行。以BTM為例,假設當T=10 h時,BTM的1系故障,車載設備實時可靠性的變化趨勢如圖6所示。 圖6 BTM1系失效對車載設備的可靠性影響 由仿真結果可以發現,系統可靠性的下降速度在BTM的1系發生故障后加快;在1系發生故障的狀態下連續運行10 h之后,系統的可靠度下降至0.9以下。因此,在現實情況下需要盡量提高該模塊的可靠性。 在運行過程中,系統不可避免地會發生故障,故障發生的原因大部分是由于系統內部自身的結構因素以及外界環境的干擾。外界環境的干擾主要是運行環境方面,如極端的天氣情況(降雪、大風、霧霾、雷擊等)。內部因素主要是由于系統連續不間斷的運行,內部硬件經過長時間的運行會出現零器件的磨損,線路表面老化等問題;除硬件故障外,車載設備的軟件也會發生信息丟失、程序死機等問題,這些稱為系統的不利干擾。從系統可靠性的角度來看,當系統受到不利干擾后,設備無法正常工作,從而引發系統的可靠性下降;當系統的可靠性降低到一定程度時,系統的彈性恢復能力(簡稱彈復力)開始發揮作用,通過恢復系統的基本功能來提升系統的可靠性。對于一個可靠的系統來說,當系統的某個單元發生故障時,存在備用模塊或者備用方案來恢復系統的基本功能,以保障系統的正常運行,這一過程稱為系統的彈復過程。在彈復過程中系統可靠性的變化趨勢如圖7所示。 圖7 系統彈復過程的可靠性變化 彈復力是對系統響應故障失效能力的一個量化,也是側面表征系統可靠性大小的一個參數指標,即系統的彈復能力越大,說明系統的可靠性程度越強。系統的彈復力與可靠性的結構關系如圖8所示。 圖8 彈復力與可靠性的關系 本文將列控系統的彈復力定義為:系統在正常運行狀態過程中,由于系統內部潛在故障或外部突發干擾引起系統功能中斷的情況下,系統內部被動或由外部主動因素進行系統狀態修復,再恢復到正常運行狀態的響應能力。 系統的彈復過程可以大致分為3個過程:(1)運行前期:正常運行階段,此階段是系統功能全部正常的時期。(2)調整期:此階段由于不利干擾的存在,導致系統的部分功能或是大分部功能失效,此時,系統自發地采取如切換至備用部件或進行系統重啟等措施,以保證系統的正常運行。(3)運行后期:系統恢復基本功能,該階段是系統通過自身的恢復措施進行調整后,恢復到基本正常狀態的階段。在運行前期,系統的各個部件正常運行。在調整期間,由于不利干擾的出現,致使系統功能部分失效而無法保證其正常運行,故障發生的原因可能是系統的硬件設備發生故障或是軟件運行錯誤等。運行后期,系統通過自身的調整基本恢復至正常狀態。在彈復過程中系統功能變化如圖9所示。 圖9 彈復過程中系統功能的變化 為了能夠有效地測量系統的彈復力大小,文獻[1]提出了一種用于評估社區應對地震發生的彈復能力的概念模型,之后文獻[14]又提出了“彈性三角”的概念,如圖10所示。 圖10 彈性三角模型 三角形的縱軸表示系統在遭遇干擾后系統功能的減少百分比,橫軸表示恢復所需要時間。圖10中橫坐標表示系統工作時間,td表示干擾發生的時間;tr表示系統功能恢復到正常狀態的時間;縱坐標表示系統完成正常功能的能力,定義P0為發生干擾時系統的可靠度大小。 文獻[15]在文獻[1]的基礎上提出了一種更為精確的用于評估系統彈復能力的綜合模型,該模型被用于評估醫院網絡的彈復力水平,最終的評估結果被作為提高醫院彈復能力水平的決策依據。 在用于評估基礎設施的彈復能力時,文獻[2]定義了彈復力的計算公式為 (10) 式中:TRE=tr-td表示系統從干擾造成的中斷恢復到正常狀態所需要的時間;Q(t)表示完成正常功能的能力,規定系統正常狀態下Q(t)=1。Q(t)定義為[16-17] Q(t)=1-L[H(t-td)-H(t- (td+TRE))]frec(t) (11) 式中:L為系統在發生干擾時,可靠度降低的差值。 L=1-R(td) (12) frec為系統的恢復函數,文獻[18]針對不同的系統提出了3種類型的恢復方程,分別是線性恢復方程、三角函數恢復方程和指數函數恢復方程。其中,線性恢復方程一般應用于結構簡單的系統;三角函數恢復方程一般應用于結構較復雜且應急防護資源有限的系統;指數恢復方程一般應用于結構復雜且應急恢復體系比較完善的系統。本文采用指數方程來計算車載設備的彈復能力,定義恢復方程為 frec(t)=exp[-(t-td)(ln200)/TRE] (13) 本文采用DTBN對車載設備在運行過程中的可靠性進行分析,針對車載設備在兩種工作模式下的可靠性大小進行定量計算,并以BTM模塊為例,分析了車載設備中冷備模塊的1系發生故障時,系統可靠度的整體變化趨勢。根據系統彈復能力計算公式可知,在計算車載設備的彈復能力時,需確定車載設備發生故障時刻的可靠度大小;基于前一部分對車載設備可靠性分析的基礎上,計算行車過程中車載設備發生故障后系統的彈復能力。 由于系統受到不利干擾而引發的設備故障,按照維修所需的時間可分為短期維修和長期維修兩種類型。本文對運行過程中的車載設備進行分析,實時性要求較高,所以重點對短期維修性故障進行分析,該故障類型可分為短期可恢復故障和短期不可恢復故障兩種。本文針對這兩種故障對車載子系統的彈復能力進行評估。 短期可恢復故障是指當車載設備的某個模塊發生故障時,存在備用部件或后備方案來保證車載設備的正常運行。 對于BTM模塊,由于采用了冗余結構,每套CTCS-300H型列控車載設備包含兩個BTM。在運行過程中,一個工作,一個處于冷備狀態。因此,當1系發生失效時,可以通過司機手動切換BTM的手段使系統切換到2系,從而保證系統可以在短時間內恢復到正常狀態。在列車運行過程中,假設在T=30 h時,由于干擾導致BTM的1系狀態異常進而發生失效,則系統的功能恢復曲線如圖11所示。 圖11 BTM1系故障時車載設備的功能恢復曲線 其中,當T=30 h時,通過建立的離散時間貝葉斯網絡,以及在C3工作模式下各個模塊的失效率,計算出此時系統的可靠度為0.801 5,因此計算出L的值為0.198 5。根據式(10),計算當發生該類型故障時,車載系統的彈復能力為96.32%。 對于制定了后備方案的短期可恢復故障,如RTM模塊失效。已知車載設備的無線傳輸模塊由RTM、無線電臺和電臺天線組成。當車載設備報無線電臺連接超時,會引起RTM模塊發生失效,此時系統無法在C3控車模式下運行,列車會采用不停車降級運行的措施,即由C3控車模式降至C2控車模式,從而在保證列車運行安全的情況下,提高行車效率。假設在T=30 h時,車載設備報無線連接超時,即RTM模塊失效,則車載設備的功能恢復曲線如圖12所示。 圖12 無線連接超時情況下車載設備的功能恢復曲線 根據式(10),計算出此時車載系統的彈復能力為96.32%。綜上所述,當發生短期可恢復故障時,系統可以較好地恢復到原正常狀態。 對于短期不可恢復故障,如車載設備的RLU模塊發生失效,此時車載設備的系統功能曲線如圖13所示。 圖13 短期不可恢復故障 如圖13所示,當車載子系統發生不可恢復的故障時,其恢復時間可近似為無窮大,即TRE=∞,則frec的值取1,同時L也取值為1。依據式(11),Q(t)的值為0,通過式(10)得出此時車載設備的彈復能力為0。 通過對車載設備的分析,從減少系統的彈性復原時間、降低系統的故障率等方面加以考慮,具體的改進措施和維修策略如下: (1)在車載設備的設計初期,對于系統中的關鍵性模塊,應提高其冗余程度,如在車載設備的運行過程中,若某個主要模塊或單元失效時,存在備用部件以保證系統的可靠運行。 (2)選擇合適的冗余方案,在確保列車安全運行的前提下,同時考慮運行效率和生產成本,對不同的模塊采取合理的冗余方式,最大限度地提升系統的復原能力。 (3)結合歷史經驗,設置消息報警機制,在車載設備的運行過程中,對于可能遇到的干擾采取提前報警的措施。 (4)建立一整套故障響應服務體系,在系統發生故障后可以快速地對故障進行應對處理,以保障系統的可靠運行。 (5)當多個模塊同時發生故障時,優先針對影響范圍大的模塊或單元進行修復,以降低故障對整個系統的影響,從而盡可能保障系統的正常運行。 相對于車載設備來說,關鍵的模塊或單元應采用冗余的設計方式,對于車載設備功能影響程度較大的模塊采用熱備的冗余方式,而影響程度相對較小的則采用冷備的冗余方式。 本文在定義了彈復力概念的同時,采用離散時間貝葉斯網絡方法,對列控系統的車載子系統展開了可靠性分析,并針對車載設備在運行過程中發生不同類型故障時的彈復能力進行定量計算。根據分析結果提出了基于彈復力效應的故障恢復策略。本文為車載設備的彈復能力評估提供了參考,對后續的設備維修和日常管理提供了理論依據,在降低系統故障率的同時也降低了系統發生故障所造成的損失。 本文只針對車載設備硬件的功能可靠性和彈復能力進行分析,結果表明車載子系統在發生短期可恢復故障的情況下,能夠較好地恢復到系統的正常狀態,從而保證車載設備的可靠運行。 參考文獻: [1]TAMVAKIS P,XENIDIS Y.Resilience in Transportation Systems[J].Procedia-Social and Behavioral Sciences,2012,48:3441-3450. [2]BRUNEAU M,CHANG S E,EGUCHI R T,et al.A Framework to Quantitatively Assess and Enhance Seismic Resilience of Communities[J].Earthquake Spectra,2003,19(4):733-752. [3]DEKKER S,HOLLNAGEL E.Resilience Engineering:New Directions for Measuring and Maintaining Safety in Complex Systems[D].Lund:Lund University School of Aviation,2010. [4]STEEN R,AVEN T.A Risk Perspective Suitable for Resilience Engineering[J].Safety Science,2011,49(2):292-297. [5]KALLANTZIS A,SOLDATOS J,LAMBROPOULOS S.Linear Versus Network Scheduling:a Critical Path Comparison[J].Journal of Construction Engineering and Management,2007,133(7):483-491. [6]中國鐵路總公司.列控車載設備典型故障案例[M].北京:中國鐵道出版社,2013. [7]袁敏.基于彈復力的列控系統可靠性實時分析方法研究[D].北京:北京交通大學,2016. [8]勞沙德.系統可靠性理論:模型、統計方法及應用[M].北京:國防工業出版社,2010. [9]周忠寶,周經倫,孫權.基于離散時間貝葉斯網絡的動態故障樹分析方法[J].西安交通大學學報,2007,41(6):732-736. ZHOU Zhongbao,ZHOU Jinglun,SUN Quan.Dynamic Fault Tree Analysis Method Based on Discrete-time Bayesian Networks[J].Academic Journal of Xi'an Jiaotong University,2007,41(6):732-736. [10]ZIO E,GUEDES S C.Safety and Reliability for Managing Risk[J].Reliability Engineering & System Safety,2008,93(12):1779-1780. [11]邸麗清,袁湘鄂,王永年.CTCS-3級列控系統RAM指標評價方法研究[J].中國鐵道科學,2010,31(6):92-97. DI Liqing,YUAN Xiange,WANG Yongnian.Research on RAM Index Evaluation Method of CTCS-3 Train Control System[J].China Railway Science,2010,31(6):92-97. [12]中國鐵路總公司.高速鐵路信號維護規則[M].北京:中國鐵道出版社,2016:14-15. [13]SU H S,CHE Y L.Reliability Assessment on CTCS-3 Train Control System Using Fault Tree and Bayesian Network[J].International Journal of Control and Automation,2013,6(4):271-291. [14]TIERNEY K,BRUNEAU M.Conceptualizing and Meas-uring Resilience:a Key to Disaster Loss Reduction[J].TR News,2007,250:14-17. [15]ZOBEL C W.Representing Perceived Tradeoffs in Defining Disaster Resilience[J].Decision Support Systems,2011,50(2):394-403. [16]CIMELLARO G P,FUMO C,REINHORN A M,et al.Quantification of Seismic Resilience of Health Care Facilities[J].Engineering Structures,2009,75(3):2221-2239. [17]CIMELLARO G P,REINHORN A M,BRUNEAU M.Framework for Analytical Quantification of Disaster Resilience[J].Engineering Structures,2010,32(11):3639-3649. [18]CIMELLARO G,REINHORN A,BRUNEAU M.Seismic Resilience of a Hospital System[J].Structure & Infrastructure Engineering,2010,6(1):127-144.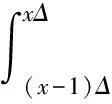
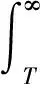
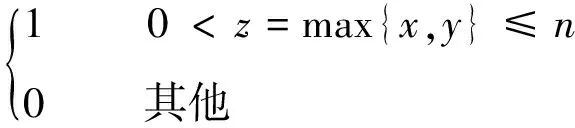
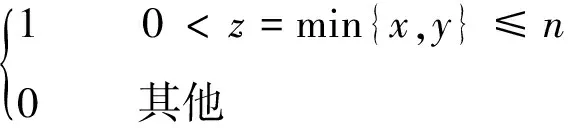

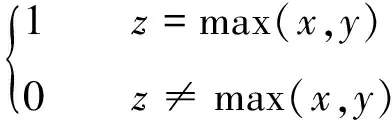
1.2 車載設備的離散時間貝葉斯網絡構建

1.3 車載設備的可靠性分析
1.4 子模塊的可靠性分析
1.5 車載設備的可靠性實時變化分析
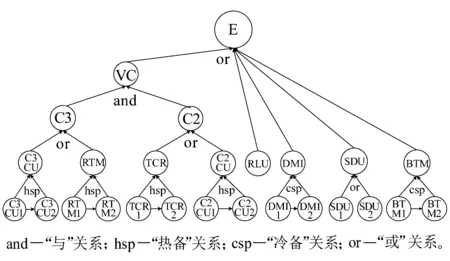
2 基于彈復力的列控車載設備可靠性分析
2.1 系統彈復力的定義

2.2 系統的彈復力評估方法

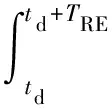
2.3 系統彈復能力評估實例分析

2.4 基于彈復力效應的故障恢復策略
3 結束語

