磁浮式軌道振動俘能機理與試驗研究

高鳴源，王 平

(西南交通大學 高速鐵路線路工程教育部重點實驗室，四川 成都 610031)

截至到2017年年底，全國鐵路的營業里程達到12.7萬km，居世界第二位；其中高鐵運營里程超過2.5萬km，居世界第一位，占世界高鐵總里程的60%以上。隨著鐵路線路的延展，鐵路監測設施和傳感器件的需求日益增長。目前軌道監測設備都需要外部供電，供電方式有兩種：有線供電和無線供電。有線供電方式采用電線電纜對監測設備進行供電，需要布設電網和電站等基礎設施，耗資較大；無線供電方式采用蓄電池等移動電源，不依賴電網等基礎設施，但需要定期對電池進行充電或更換，充電作業無法在現場完成，維護養護成本高[1]。低成本、少維護的新型供電方式成為未來發展的趨勢。利用列車通過時軌道振動產生的能量發電，不僅可節省大量基建投資而且節能環保，具有較好的應用前景。

國內外利用振動能量進行發電的技術研究可追溯到20世紀90年代，大體可分為三類技術：靜電式發電、壓電式發電和電磁式發電[2-15]。靜電式發電的研究最早由美國加州理工大學的學者開始，文獻[2]利用駐極永極體材料可永久保持電荷的特性，結合微機電加工工藝，研制出一種微型的彈簧條支撐式可變電容器件，其電容的電極上涂覆有駐極永極體材料，伴隨著外界環境的振動，電容的面積發生變化，在回路上激發出電流，產生的電流隨后被收集并用來向其他器件供電。雖然靜電式發電方法目前已在微振動發電領域得到較多成功應用，但是它對靜電駐極體材料和工藝的要求較高[10]，目前我國廠家不具備駐極體材料的生產能力，因此國內軌道振動發電領域普遍未采用靜電式發電方式。

壓電式發電是目前研究相對較多的發電方式。文獻[16]提出一種技術方案，通過在軌下膠墊底部設置壓電換能材料，將輪對-鋼軌作用位移轉換為電能，實現能量收集。文獻[17]提出一種壓電鼓式結構，置于軌枕下方，以1∶10列車軌道模型進行室內試驗。壓電式發電技術具有靈敏度高的優點，但由于現有壓電材料的內阻較大，負載能力較弱，因此發電量偏小[18-20]，難以滿足軌道監測設備的供電要求，其實用化進程受到壓電材料效能的制約。

電磁式發電方式可以在低頻范圍產生較大的功率輸出，對材料無特殊需求，是一種有望在短期內進入實用化階段的技術。現行電磁式軌道振動發電方式研究可分為共振式和機械式兩種。共振式的代表性工作：文獻[21]開展音圈線圈式和懸臂式發電機用于軌道能量收集的研究；文獻[22]從理論上探討列車經過時，單自由度線性諧振換能器的瞬態響應特性。機械式的代表性工作參見文獻[23-25]，其原理為置于軌枕之上的機械式發電裝置，通過齒輪齒條等機械傳動機構將軌道結構的垂向振動轉變為機械結構的旋轉運動，進而帶動電磁式電機發電，并在室內和木枕軌道上進行試驗。僅當軌道振動頻率與設定的頻率匹配時共振式電磁發電才能獲得較高的發電效率，而實際線路上機車車輛、運行速度及軌道結構等的不同將導致軌道振動頻率在較寬的頻帶內變化，成為制約共振式發電效率的控制性因素。機械式發電方式對振動頻率無特殊要求，但是要求有較大的振動位移(文獻[24]公布的試驗數據振動位移為6.4～19 mm，文獻[26]的振動位移為6 mm)，隨著我國鐵路建設標準的大幅度提高，干線鐵路軌道振動位移幅值明顯減小(無砟軌道通常小于2 mm，有砟軌道通常小于3 mm[27])，將影響機械式發電方式的發電效率。綜上，這兩種電磁式發電方式對軌道振動參量的要求與軌道運行實際工作狀態不符，成為它們進入實用化階段的瓶頸。

針對現行電磁式軌道振動發電方式的不足，本文提出一種基于磁浮式換能原理的電磁式軌道振動發電技術。磁浮式換能的原理是利用懸浮磁體切割磁力線發電，懸浮磁體與靜止磁體之間的電磁作用力隨著磁體間距離的變化呈現非線性硬剛度特性，因此可以在寬頻帶內對激勵產生響應；懸浮磁體的運動由電磁力約束，無需彈簧、彈條等機械元件，因此也具有靈敏度高的特點。磁浮式換能可以克服上述共振式和機械式電磁發電方式的缺點。

本文建立軌道振動-電磁耦合動力學模型(包括磁浮式換能器非線性有阻尼動力學方程)，為磁浮式振動換能器的設計提供理論依據和指導；提出磁浮式振動換能器的系統設計，介紹試驗研究方法和試驗設置；討論理論計算結果與試驗測試結果，研究表明磁浮式振動換能系統具有非線性硬剛度特性，可在寬頻帶范圍有效收集軌道振動能量。

1 理論模型

軌道振動-電磁耦合動力學模型的體系架構如圖1所示。首先，基于輪軌耦合動力學模型計算車輛行駛載荷激勵下軌道的動力響應，即計算軌道振動加速度、振動速度和振動位移的動力時程。其次，將軌道動力學計算結果作為輸入，代入磁浮式振動換能器非線性有阻尼動力學方程(圖1中虛線框所示方程)，計算磁浮式換能器系統的動力響應。其中，磁浮式換能器的非線性剛度參數由麥克斯韋應力張量法計算，采用顯式積分法求解磁懸浮振子的非線性振動微分方程，采用非線性理論中的多尺度法計算磁浮式振子的幅頻響應。最后，將磁浮式換能器懸浮振子的動力響應作為輸入代入麥克斯韋電動力學方程組進行求解，求得發電量。

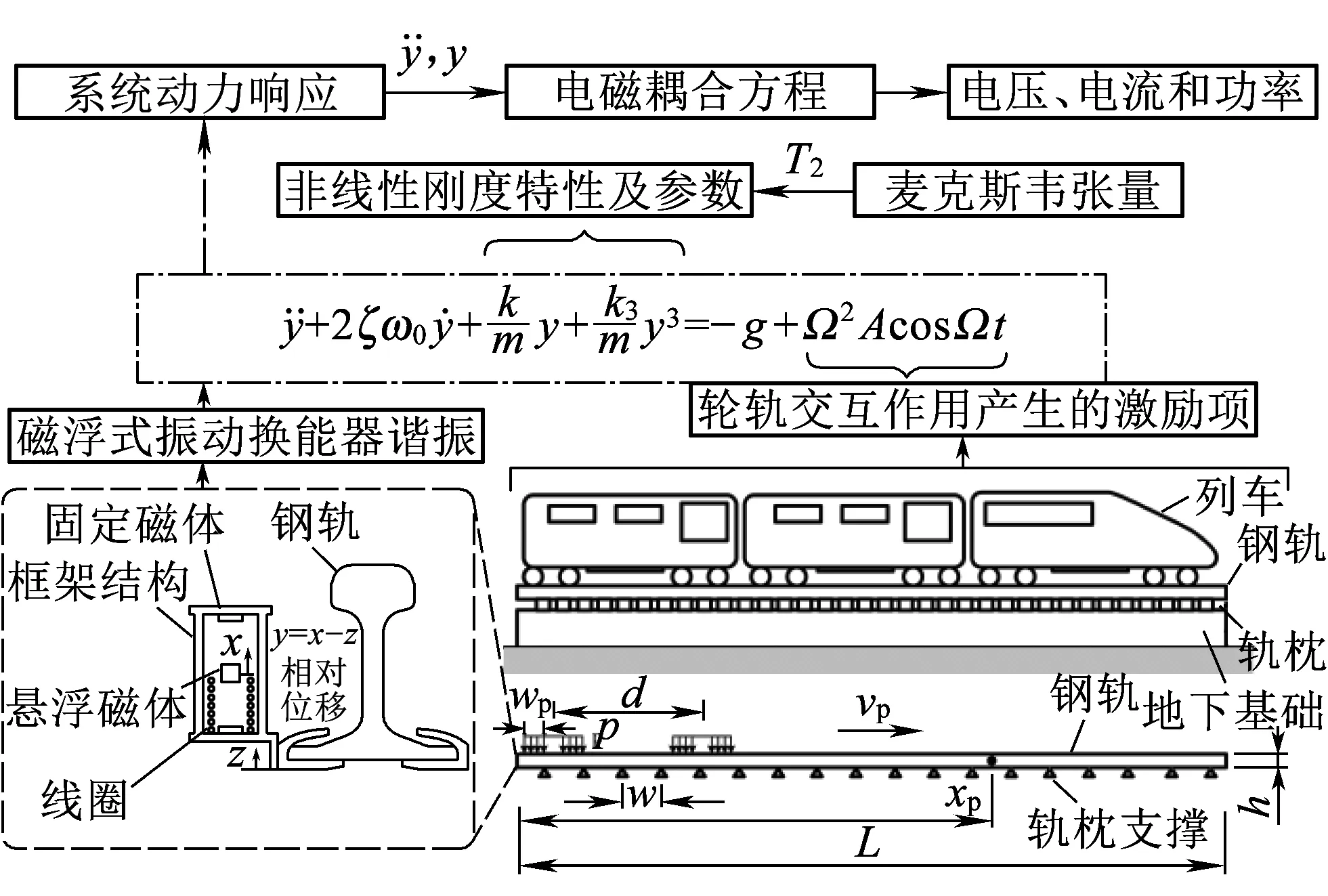
圖1 軌道振動-電磁耦合動力學模型架構

利用該模型，可以計算各類機車車輛以及不同運行速度下各類軌道結構的發電能力，為磁浮式軌道振動俘能系統的設計提供理論依據。

1.1 車輛-軌道耦合動力學模型

車輛-軌道耦合動力學模型包括兩個子系統，其中車輛子系統被建模為在軌道上以恒定速度移動的10自由度系統，如圖2所示。軌道子結構由三層(鋼軌、軌枕和道床)組成，被假設為連續彈性離散點支承上的無限長歐拉-伯努利梁。這兩個子系統之間的輪軌相互作用服從赫茲非線性彈性接觸理論。利用數值積分方法可計算系統的動力響應。車輛模型參數參見文獻[27]中的高速模型車(HSC)模型。

圖2 車輛-軌道耦合動力學模型(附有磁浮式振動換能器)

對于安裝有電磁式振動換能器的鐵路軌道，振動換能器剛性連接于鋼軌軌底，可視為軌道的附加質量，需計算鋼軌的附加質量和附加慣性矩，其幾何參數如圖2所示。每米鋼軌振動換能器的附加質量為15 kg，軌道模型參數參見文獻[27]中的長枕埋入式無砟軌道模型。

1.2 磁浮式振動換能器非線性有阻尼動力學方程

磁浮式振動換能器非線性有阻尼動力學方程為

( 1 )

式中：y=x-z為懸浮磁體質量塊的相對位移，x為懸浮磁體的絕對位移，z為固定磁體的絕對位移；ζ為阻尼比；ω為系統固有頻率；β為立方剛度系數；F0為懸浮磁體的重力加速度；F1為激勵加速度幅值；Ω為激勵頻率；t為時間變量。其中ζ、ω、β、F0、F1可以由式( 2 )～式( 6 )得到。

( 2 )

( 3 )

( 4 )

F0=g

( 5 )

F1=Ω2A

( 6 )

式中：c為系統的阻尼系數；k為系統線性剛度；k3為系統非線性剛度；m為懸浮磁體的質量；g為重力加速度；A為激勵位移幅值。

采用非線性理論中的多尺度法求解上述方程。多尺度法的思想是對自變量采用多種不同的變化尺度漸進展開求解。引入(M+1)個不同尺度的時間變量

Tm=εmtm=0，1，2，…，M

( 7 )

y為(M+1)個獨立自變量的函數，不再是單個自變量t的函數，即

y(t；ε)=t(T0，T1，…，TM；ε)=

( 8 )

隨著m的增加，自變量Tm隨時間t變化的速度依次減小一個數量級。M的值取決于求解時保留的階數。本文引入2個不同尺度的時間變量，即取M為1。忽略高階無窮小量，則有

y(t；ε)=y0(T0，T1)+εy1(T0，T1)

( 9 )

式( 1 )可改寫為

(10)

其中ε為小參數

2εμ=2ζω

(11)

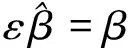
(12)

(13)

通過引入不同尺度的時間變量，使得對于時間t的導數變為對于Tm的偏導數展開式

(14)

(15)

將上述方程代入非線性振動方程，就能按ε的冪次得到各階求解方程，即關于y0，y1，…，yM的方程組，各方程的解中包含不同尺度時間變量T0，T1，…，TM的任意函數。

(16)

(17)

(18)

(19)

利用消除永年項得到附加條件

-2iω[A(T1)′+μA(T1)]-

(20)

引入極坐標

(21)

-iω[a′+aiφ′+μa]-

(22)

γ=σT1-φ

(23)

(24)

(25)

(26)

可以得到非線性有阻尼動力學方程的激勵位移幅值A與激勵頻率Ω之間的關系為

(27)

式(27)可用來計算磁浮式非線性換能器的幅頻響應特性。

另外，我們還需要計算磁浮式非線性換能器的時域響應，式( 1 )可以改寫為

(28)

BncosnΩ(t-t0)]

(29)

式中：A0、N、An、Ω、t0、Bn(n=1，2，…，N)為通過傅里葉級數曲線擬合定義的常數。

為了獲得時域的振動響應，我們采用顯式積分法求解磁懸浮振子的非線性微分方程。軌道振動激勵采用傅里葉級數表示。

1.3 軌道振動激勵下電磁耦合方程

麥克斯韋電磁耦合方程可寫為

(30)

(31)

式中：Br為懸浮磁體表面磁通密度；v為導電體的速度；Je為電流密度；σ為電導率；μ0為真空的磁導率；μr為介質的相對磁導率；B為磁感應強度；E為感應電動勢。

式(30)、式(31)可用于計算換能器產生的感應電壓Vind，換能器對負載電阻Rload的輸出功率為

(32)

其中線圈的內阻Rcoil為

(33)

式中：N為線圈匝數；L為線圈截面外圈的周長；σcoil為線圈導線的體積電導率；acoil為線圈導線截面面積；Acoil為線圈截面的面積。換能器的阻尼系數可由式(34)計算。

(34)

式中：Lcoil為線圈電感；Fdamp為阻尼力。阻尼比為

(35)

2 換能器設計與試驗

2.1 磁浮式振動換能器設計

磁浮式振動換能器的設計如圖3所示。兩個靜止磁體分別固定于上下鋁軸套上。上下鋁軸套機械連接到聚甲基丙烯酸甲酯(PMMA)管上。在兩個靜磁體之間的PMMA管中心位置放置一個懸浮磁體，磁體的磁極方向設置為排斥中心懸浮磁體，使中心磁體懸浮在PMMA管內。懸浮磁體與靜止磁體的距離可以通過改變磁體的表面磁感應強度調整。PMMA管的外環安裝有銅線圈，線圈匝數和線圈幾何尺寸可調。PMMA管協同支撐環一起固定在支座上，固定支座一側留螺栓孔，可通過螺栓將其固定在鋼軌夾持器的一側。鋼軌夾持器由兩獨立U形夾持塊組成，夾持塊底部具有貫通的螺栓孔，安裝時將夾持塊置于軌底兩側，通過長螺栓將兩夾持塊連接成整體，并夾緊軌底，實現振動換能器與鋼軌的連接。鋼軌的振動加速度會傳遞到固定支座上，作為振動換能器的激勵，進一步激發懸浮磁體產生動態響應。

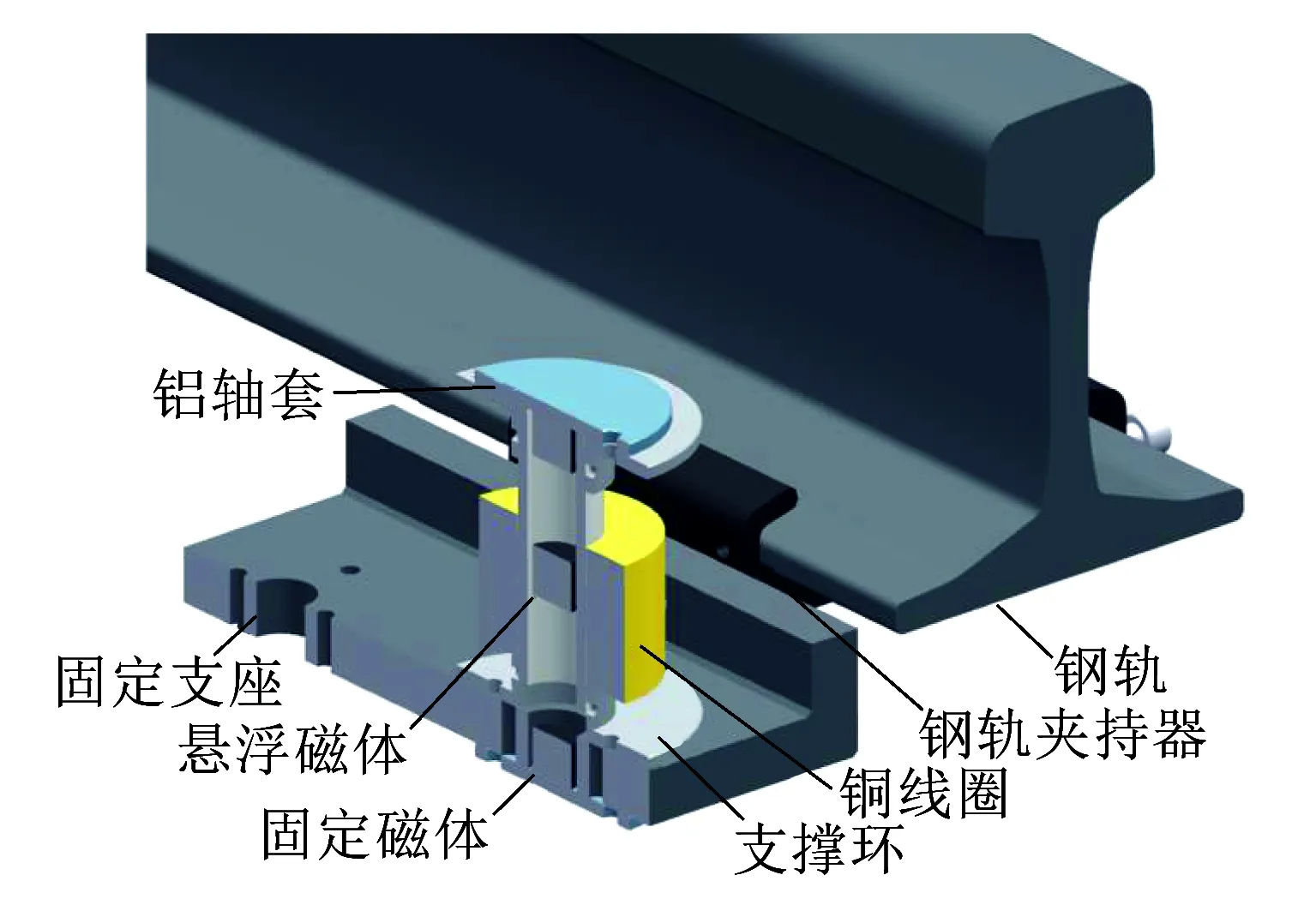
圖3 磁浮式振動換能器設計

2.2 磁浮式軌道振動俘能試驗

磁浮式軌道振動俘能裝置的掃頻振動測試如圖4所示。該測試的目的是評估磁浮式振動換能器的有效工作頻帶。根據文獻[28]的規定，選擇兩個頻率范圍(5～200 Hz和5～500 Hz)，加速度幅值設定為2g和4g。文獻[28]規定了在交越頻率(振動試驗中，振動特征控制量由位移轉變為加速度時的頻率值)以下的恒定位移幅值激勵和在交越頻率以上的恒定加速度幅值激勵，掃頻10次，掃頻速率為每分鐘一個倍頻。交越頻率由激振器本身的激勵機理決定，理想情況下應始終采用恒定加速度激勵，但是在起始掃頻時，維持恒定加速度需要較大的振動位移，因此需要一個頻率段從恒定位移激勵過渡到恒定加速度激勵。采用兩種懸浮磁體，質量分別為61.4 g和122.8 g。設置兩個集成電子壓電加速度計(IEPE)，分別控制振動臺的振動激勵和監測磁浮振子的動態響應，其中控制用加速度傳感器的靈敏度為9.71 mV/g，監測用加速度傳感器的靈敏度為9.73 mV/g。磁浮式振動換能器參數及試驗設置見表1。設置了3種工況，工況1和工況2具有相同的非線性剛度k3，工況1和工況3具有相同的線性剛度k，工況1和工況2采用相同質量的懸浮磁體，工況3懸浮磁體的質量是工況1、工況2的兩倍。3種工況的幾何尺寸均需滿足文獻[29]的要求。

圖4 磁浮式軌道振動換能器掃頻振動試驗1—監測用IEPE加速度傳感器；2—懸浮磁體；3—銅線圈；4—控制用IEPE加速度傳感器；5—電源裝置；6—控制軟件界面；7—振動控制器；8—磁浮式振動換能器；9—振動臺；10—示波器；11—數據記錄終端。

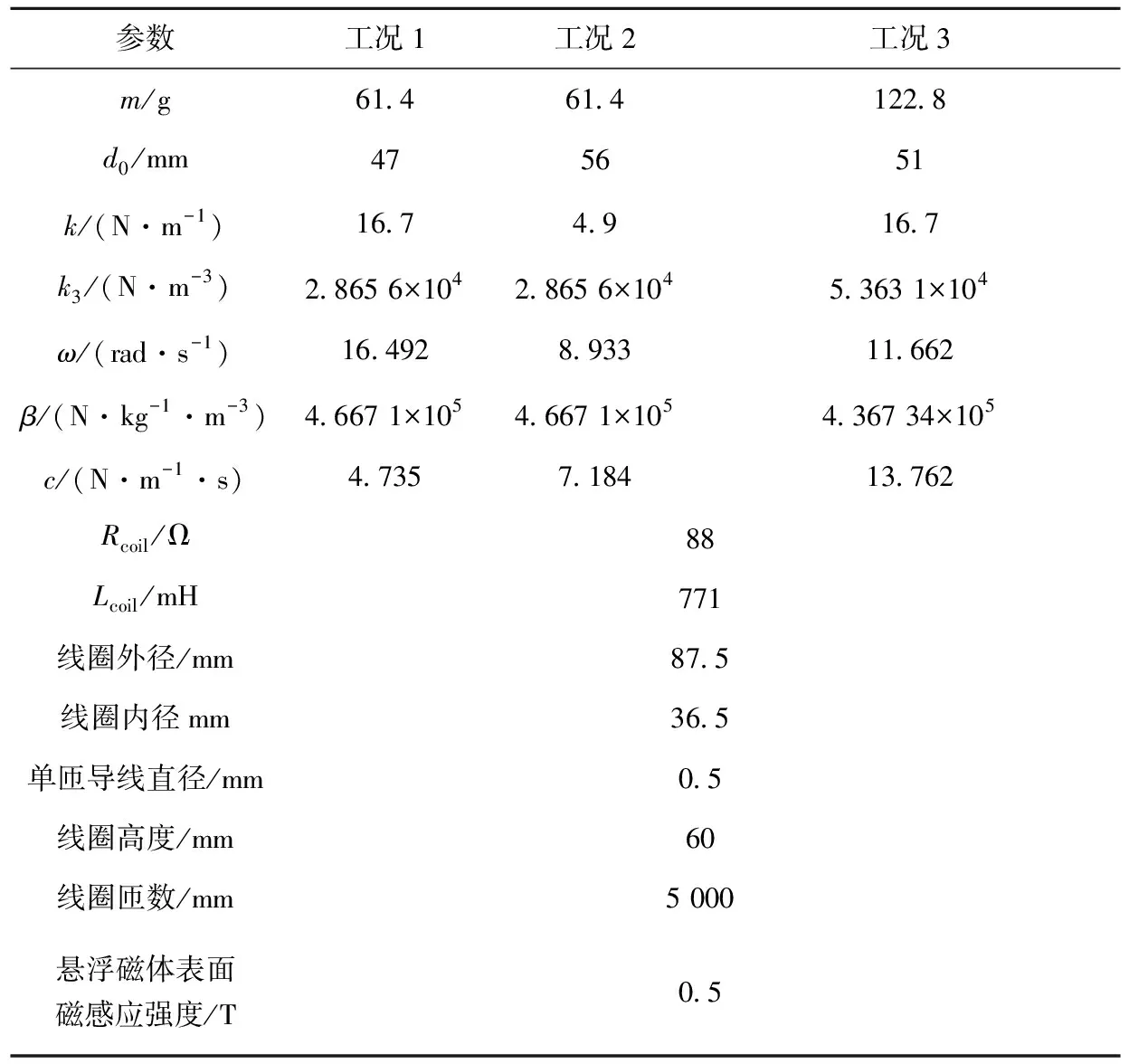
參數工況1工況2工況3m/g61.461.4122.8d0/mm475651k/(N·m-1)16.74.916.7k3/(N·m-3)2.865 6×1042.865 6×1045.363 1×104ω/(rad·s-1)16.4928.93311.662β/(N·kg-1·m-3)4.667 1×1054.667 1×1054.367 34×105c/(N·m-1·s)4.7357.18413.762Rcoil/Ω88Lcoil/mH771線圈外徑/mm87.5線圈內徑mm36.5單匝導線直徑/mm0.5線圈高度/mm60線圈匝數/mm5 000懸浮磁體表面磁感應強度/T0.5

注：d0為磁體間的幾何距離。

試驗測試采用Tektronics公司DPO2024示波器監測輸出電壓波形，示波器探頭的正負極分別連接到振動換能器的輸出端。測試中開啟示波器的噪聲濾波功能，濾除600 kHz以上的干擾噪聲。同時示波器被用作數據采集設備，并通過Labview Signal Express軟件連接到筆記本電腦，這樣就可以激活自動觸發/記錄模式，實現連續數據采樣。數據存儲在筆記本電腦的硬盤上，供后續分析和使用。

此外，還進行了模擬輪對激勵作用下的電磁振動換能器性能測試，如圖5所示。液壓作動器可施加最高140 kN的作用力，模擬列車行經時的輪軌交互作用力。該試驗的詳細步驟及結果可參考文獻[3]。

圖5 模擬輪對激勵作用下的電磁振動換能器性能測試1—作動器；2—磁浮式振動換能器；3—數據記錄終端；4—能量轉換電路；5—示波器；6—懸浮磁體；7—銅線圈；8—IEPE加速度傳感器；9—鋼軌；10—諧振式電磁振動換能器。

3 結果與討論

懸浮磁體受到的非線性磁浮力可以采用麥克斯韋應力張量法[8]進行計算。圖6為工況1中懸浮磁體受到的非線性磁浮力及非線性剛度。由圖6可知，磁浮式振動換能器具有正的立方剛度k3，對應硬彈簧特性。線性剛度k可以通過改變懸浮磁體與靜止磁體的距離調整。

(a)非線性磁浮力(b)非線性剛度

圖6 磁浮式振動換能器非線性特性曲線

圖7(a)為CRH380A高速列車以240 km/h的速度通過無砟軌道結構時鋼軌的垂向加速度實測時程曲線。軌道為無縫線路，由Vossloh300-1彈條扣件固定，并通過軌下膠墊支撐在混凝土雙塊式軌道上。CRH380A型列車由兩節動力車和六節拖車組成，每節車由4個輪對支撐，軸距為2.5 m，車輛定距為18 m，動力車長25.7 m，拖車長25 m。CRH380A列車總長為203 m。加速計位于軌底，數據采樣頻率為12.8 kHz。圖7(b)為加速度信號的功率譜密度。圖7(b)表明鋼軌的垂向振動加速度信號在較寬的頻率范圍內具有功率譜密度分量，因此在掃頻振動試驗中采用5～500 Hz的寬頻激勵頻帶。

(a)軌道垂向振動加速度時程(b)軌道垂向振動功率譜密度

圖7 實測軌道垂向振動加速度時程曲線與功率譜密度

軌道的垂向振動速度和位移通過2.1節所述的車輛-軌道耦合動力學模型計算。輸入波長范圍為1.524～304.8 m的美國軌道譜作為軌道不平順激勵。文獻[27]比較了1～30 m波長范圍內美國軌道譜和中國三大干線譜，結論是：我國三大干線譜的高低不平順總體上大于美國五級和六級軌道譜數值，表明我國線路高低幾何狀態較差[27]。軌道振動俘能主要利用軌道的垂向振動發電，因此較好的線路幾何狀態意味著軌道振動幅值較小，對于振動發電來說更具挑戰性，因此本文選用美國軌道譜進行計算。從圖8可以看出，鋼軌的振動位移幅值通常小于2 mm。車輛行經時鋼軌振動速度幅值的峰值大于0.2 m/s。

(a)振動速度(b)振動位移

圖8 列車行經時軌道垂向振動速度與振動位移

磁浮式非線性振動換能器的幅頻響應特性曲線如圖9～圖12所示。其中圖9(a)、圖10(a)、圖11(a)和圖12(a)為只考慮機械阻尼系數(cm)的情況，圖9(b)、圖10(b)、圖11(b)和圖12(b)為同時考慮機械阻尼系數和電磁阻尼系數(ce)的情況。機械阻尼主要是由于懸浮磁體與PMMA管壁之間的機械摩擦等產生，電磁阻尼則是由于懸浮磁體在線圈中運動時受到了楞次作用力而產生。非線性振動換能系統的頻率與其振幅有關，當β>0時(硬剛度特性)，頻率隨幅值的增加而增大，這是由于系統的剛度隨著振幅增加變化的緣故。需要注意的是，電磁阻尼系數可以通過改變線圈匝數、線圈幾何形狀、線圈內阻等來調節，以符合特定的應用要求。

(a)c=cm(b)c=cm+ce

圖9 磁浮式振動換能器位移幅值-頻率響應特性曲線

圖10 磁浮式振動換能器速度幅值-頻率響應特性曲線

圖11 磁浮式振動換能器加速度幅值-頻率響應特性曲線

圖12 磁浮式振動換能器速度幅值與加速度激勵關系曲線

圖9～圖12為采用工況1參數計算的結果。機械阻尼系數為0.19，電磁阻尼系數為4.545。圖12為激勵頻率30π rad/s時，磁浮式振動換能器速度幅值與加速度激勵關系曲線。對于電磁能量收集系統，其產生的功率與電磁阻尼系數及速度響應幅值的平方成正比。電磁阻尼由設備參數(線圈匝數、線圈幾何形狀和布置、表面磁通密度等)確定，可以根據鐵路行業的具體要求進行調整。圖10(b)為懸浮振子速度響應振幅的理論預測值。在30～500 Hz范圍內，速度幅值大于0.15 m/s。電磁式振動換能器屬于阻尼元件，其感應電壓值與懸浮磁體的振動速度幅值成正比[12，14]，當其振動速度幅值大于0.15 m/s時，根據計算結果其感應電壓大于1.8 V，即可用于為DC-DC電路供電[3]，這表明在較寬的頻帶范圍內磁浮式振動換能器能夠有效收集振動能量。

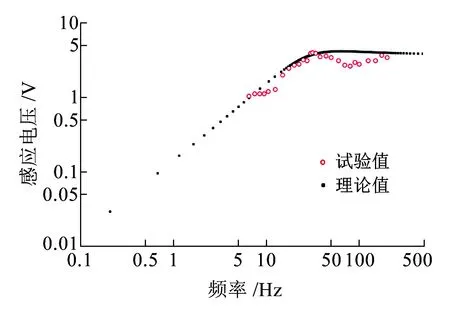
圖13 磁浮式振動換能器輸出電壓理論計算值與試驗測試結果

圖13為磁浮式振動換能器輸出電壓理論計算值與試驗測試結果的對比。在交越頻率之下，試驗結果與理論預測吻合較好。在交越頻率之上，理論預測值與測試值之間的差異隨著頻率的增加而增大。這可能是由線圈自感系數的變化以及高頻下的漏感引起的。

磁浮式非線性振動換能器的時域響應特性如圖14所示。圖14為速度240 km/h高速列車行經時的軌道垂向振動加速度和計算得出的磁浮式換能系統的感應電壓值。本文使用實測的鋼軌振動加速度信號作為計算模型(圖1)的輸入來計算系統的感應電壓。測量的加速度信號包括由軌道不平順和車輪不圓順引起的高頻分量。波峰和波谷的位置與車輛轉向架的位置相對應，感應電壓峰峰值為5 V。電磁式振動換能器是一種黏彈性阻尼器件，其感應電壓與速度幅值成正比。如圖8(a)和圖14所示，感應電壓的波形曲線與軌道振動速度的波形曲線相似。

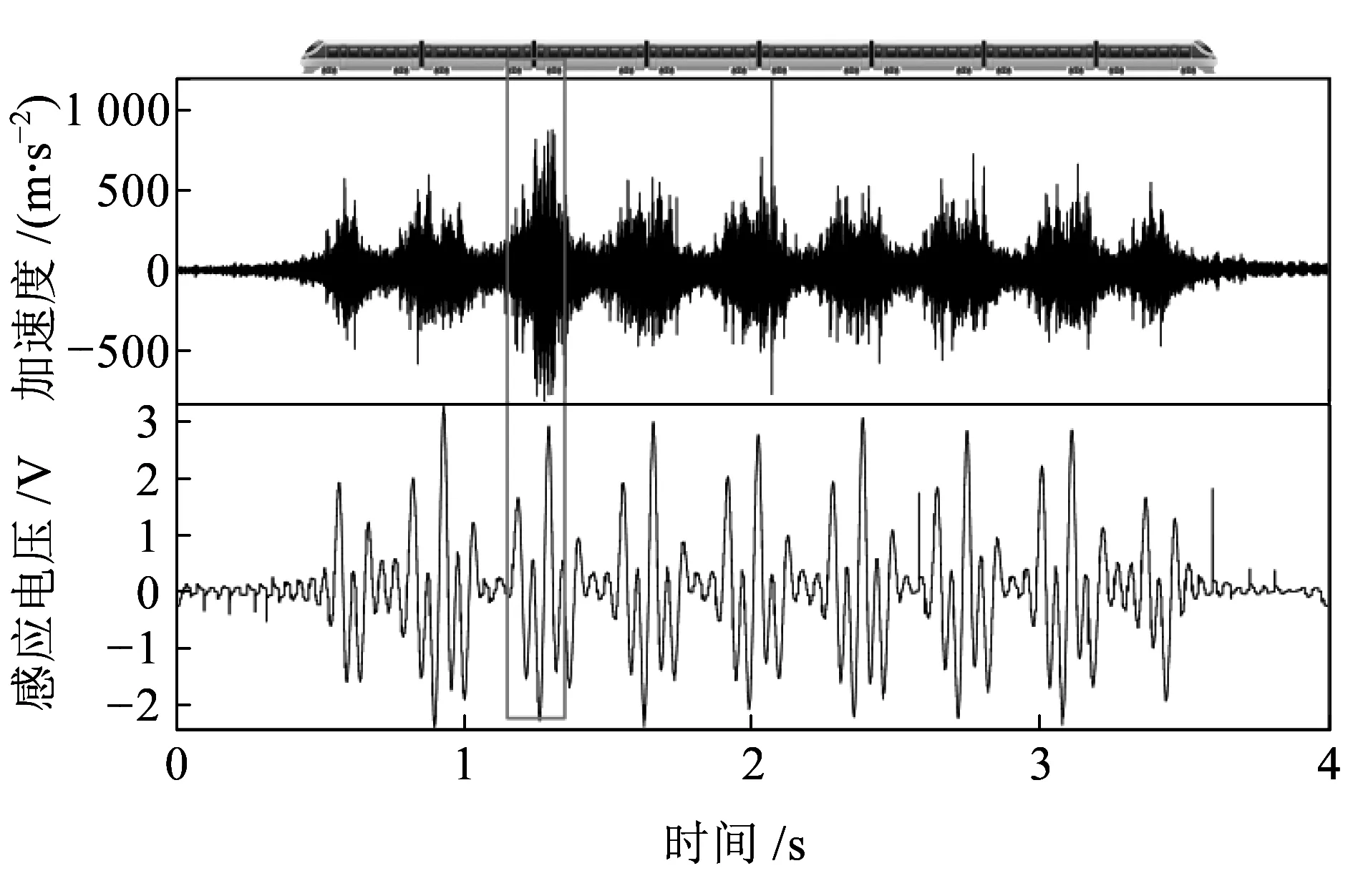
圖14 列車激勵作用下磁浮式振動換能器時域響應特性曲線

按照文獻[28]的規定開展掃頻振動試驗。在交越頻率值以下，振動臺輸入激勵為恒定位移；在交越頻率值以上，激勵條件為恒定加速度幅值。速度幅值在交越頻率處達到極大值。根據實測得到的軌道垂直加速度信號的功率譜密度，我們設定起始頻率為5 Hz，截止頻率為500 Hz。采用兩種激勵模式：激勵模式1的交越頻率為22.3 Hz；在交越頻率以下，其位移幅值為1 mm(峰峰值為2 mm)；在交越頻率以上有恒定的2g加速度激勵幅值；最大速度幅值為0.14 m/s。激勵模式2的交越頻率是31.5 Hz；在交越頻率以下，其位移幅值為1 mm(峰峰值為2 mm)；在交越頻率以上有恒定的4g加速度激勵幅值；最大速度幅值為0.198 m/s。對于兩種不同的激勵模式，其控制值在圖15～圖18中給出。采用連續掃頻，頻率隨時間呈指數變化。掃描速率為每分鐘一個倍頻，容差為±10%。

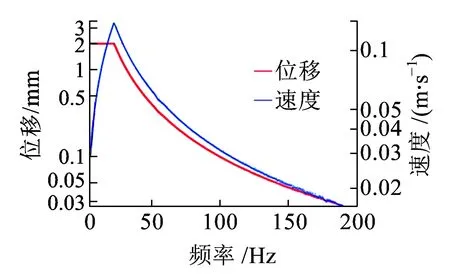
(a)位移與速度控制值

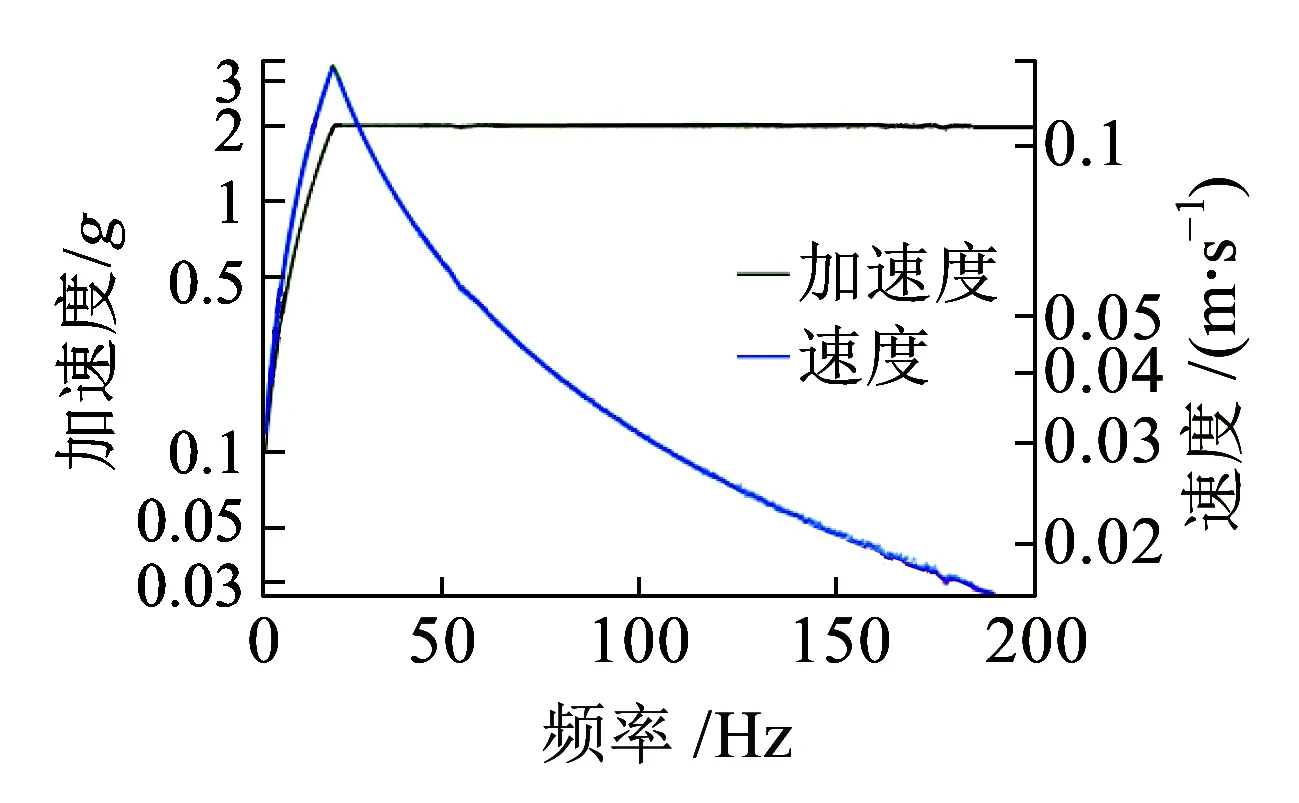
(b)加速度與速度控制值

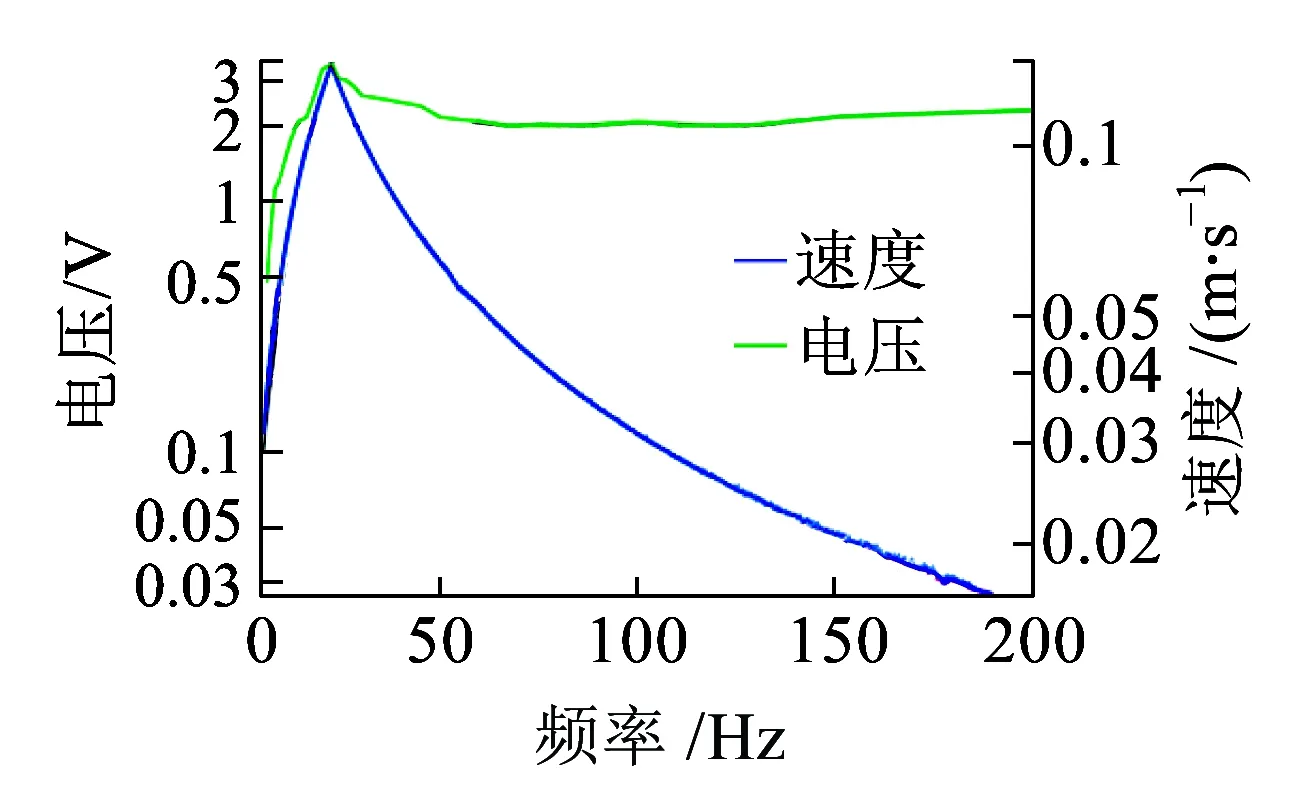
(c)電壓與速度控制值圖15 掃頻振動測試(工況2，5～200 Hz，激勵模式1)

(a)位移與速度控制值

(b)加速度與速度控制值

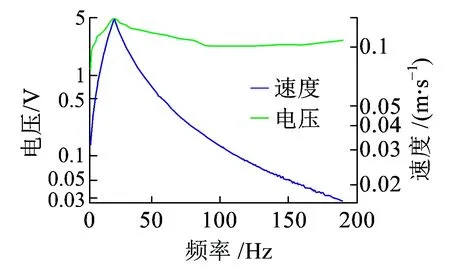
(c)電壓與速度控制值圖16 掃頻振動測試(工況3，5～200 Hz，激勵模式1)

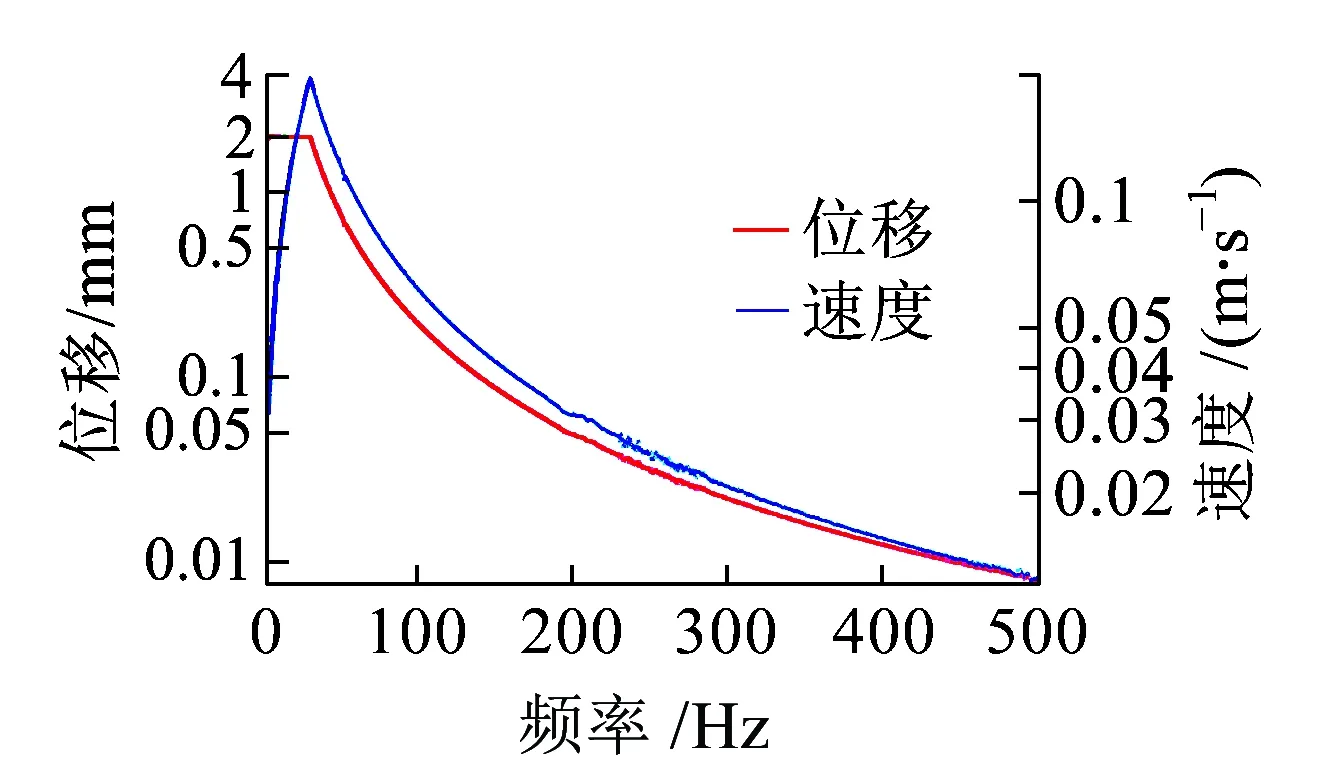
(a)位移與速度控制值

(b)加速度與速度控制值

(c)電壓與速度控制值圖17 掃頻振動測試(工況1，5～500 Hz，激勵模式2)

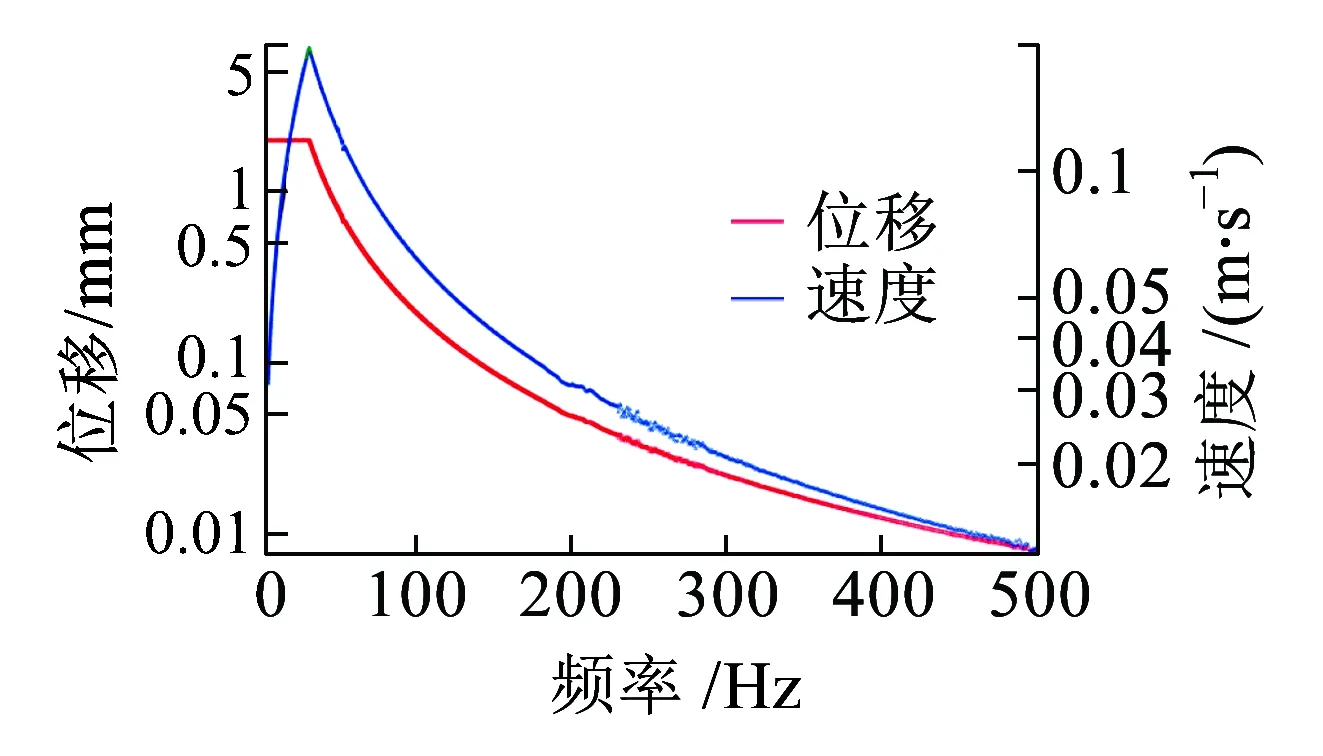
(a)位移與速度控制值

(b)加速度與速度控制值

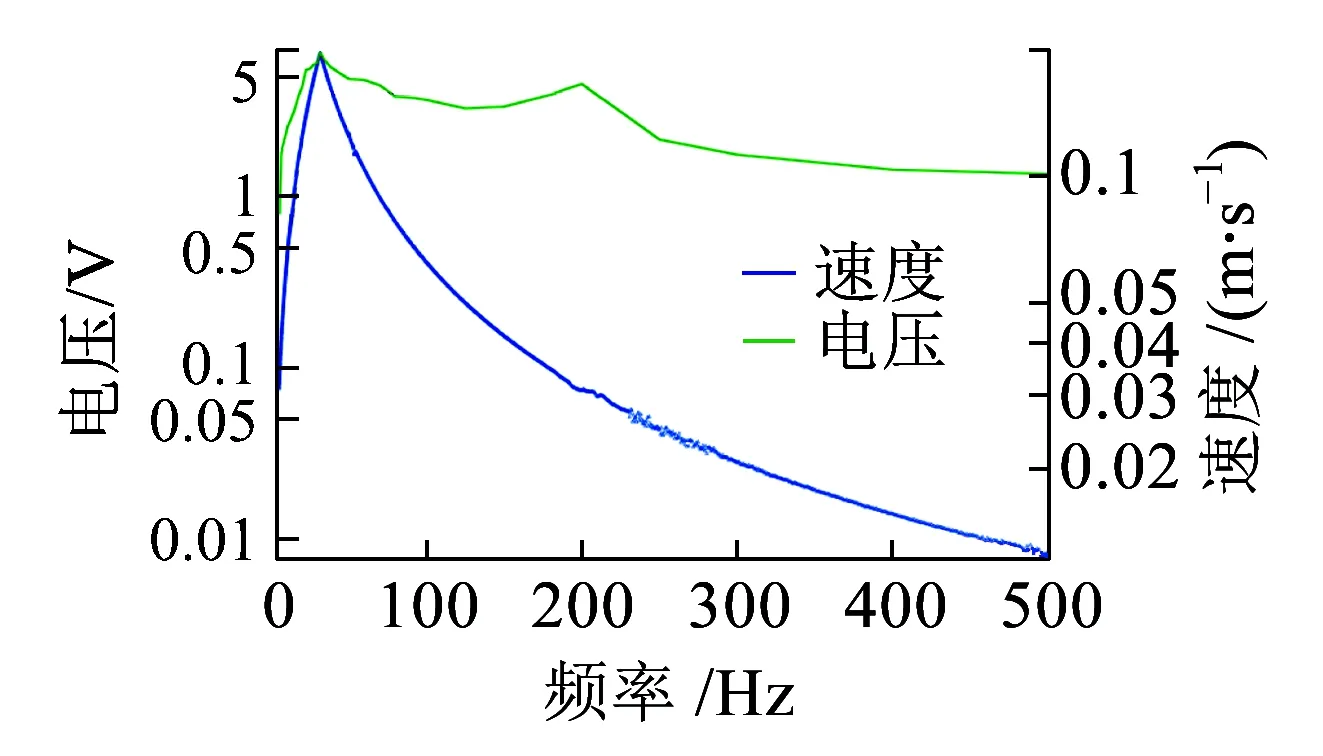
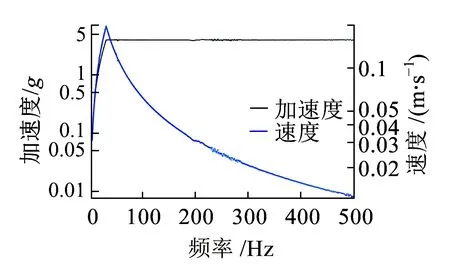
(c)電壓與速度控制值圖18 掃頻振動測試(工況3，5～500 Hz，激勵模式2)

如圖15～圖18所示，在交越頻率以上，位移激勵測量幅值隨著頻率的增加而減小。激勵速度的測量幅值最大值位于交越頻率處，激勵加速度的測量幅值在交越頻率以上具有恒定值。安裝在軌道上的振動換能器受到軌道振動加速度的激勵，因此需要設置恒定加速度激勵，以評估磁浮式振動換能系統的有效工作頻帶。對于3種工況，在較寬的頻率范圍內可獲得有效電壓值。我們使用了一個DC-DC芯片組，可在0.9～5 V的輸入電壓范圍內工作。半橋整流器的正向壓降約為0.35 V(采用肖特基二極管，它具有較低的正向壓降(IF=10 mA))，因此需要至少1.8 V的輸入電壓才能使DC-DC模塊工作。工況3具有最佳的輸出性能，最大輸出電壓為6.96 V，有效頻帶為7～500 Hz。

4 結束語

本文建立軌道振動-電磁耦合動力學模型，該模型可以計算列車行經時軌道結構的發電能力，為電磁式軌道振動俘能系統提供了理論依據和設計指導。提出并設計了磁浮式軌道振動俘能系統，理論計算和分析表明，利用其非線性剛度特性可在寬頻帶內收集軌道振動能量。開展了磁浮式軌道振動俘能系統的試驗研究，結果顯示磁浮式軌道振動俘能系統可在寬頻帶內有效俘獲軌道振動能量。該系統潛在的應用場景是軌道結構的狀態監測，可為鐵路及橋梁無線傳感器網絡的傳感器節點提供持續電力供給。

參考文獻：

[1]HODGE V J,O’KEEFES,WEEKS M,et al.Wireless Sensor Networks for Condition Monitoring in the Railway Industry:A Survey[J].IEEE Transactions on Intelligent Transportation Systems,2015,16(3):1088-1106.

[2]WILLIAMS C B,YATES R B.Analysis of a Micro-electric Generator for Microsystems[J].Sensors Actuators A:Physical,1996,52(1/3):8-11.

[3]GAO M Y,WANG P,CAO Y,et al.Design and Verification of a Rail-borne Energy Harvester for Powering Wireless Sensor Networks in Railway Industry[J].IEEE Transactions on Intelligent Transportation Systems,2017,18:1596-1609.

[4]GAO M Y,WANG P,CAO Y,et al.A Rail-borne Piezo-electric Transducer for Energy Harvesting of Railway Vibration[J].Journal of Vibroengineering,2016,18(7):4647-4663.

[5]WANG P,WANG Y F,GAO M Y,et al.Investigation on the Train Aerodynamic Performance and Energy Harvesting with Track-borne Wind Turbine[C]//Proceedings of the 96th Annual Meeting of Transportation Research Board.Washington D.C.:[s.n.],2017:17-00299.

[6]MITCHESON P D,YEATMAN E M,RAO G K,et al.Energy Harvesting from Human and Machine Motion for Wireless Electronic Devices[J].Proceedings of the IEEE,2008,96(9):1457-1486.

[7]STEPHEN N G.On Energy Harvesting from Ambient Vibration[J].Journal of Sound and Vibration,2006,293(1/2):409-425.

[8]GAO M Y,HU C Z,CHEN Z Z,et al.Design and Fabrication of a Magnetic Propulsion System for Self-propelled Capsule Endoscope[J].IEEE Transaction on Biomedical Engineering,2010,57(12):2891-2902.

[9]HOFFMAN D,FOLKMER B,MANOLI Y.Fabrication,Characterization and Modelling of Electrostatic Micro-ge-nerators[J].Journal of Micromachanics and Microengineering,2009,19(9):1489-1503.

[10]SUZUKI Y.Development of a MEMS Energy Harvester with High-performance Polymer Electrets[C]//Proceedings of Power MEMS,2010.

[11]ERTURK A,INMAN D J.An Experimentally Validated Bimorph Cantilever Model for Piezoelectric Energy Harvesting from Base Excitations[J].Smart Materials and Structures,2009,18(2):025009.

[12]LESIEUTRE G A,OTTMAN G K,HOFMANN H F.Damping as a Result of Piezoelectric Energy Harvesting[J].Journal of Sound and Vibration,2004,269(3/5):991-1001.

[13]DONELAN J M,LI Q,NIANG V,et al.Biomechanical Energy Harvesting:Generating Electricity during Walking with Minimal User Effort[J].Science,2008,319:807-810.

[14]MANN B P,SIMS N D.Energy Harvesting from the Nonlinear Oscillations of Magnetic Levitation[J].Journal of Sound and Vibration,2009,319(1/2):515-530.

[15]BEEBY S P,TORAH R N,TUDOR M J,et al.A Micro Electromagnetic Generator for Vibration Energy Harvesting[J].Journal of Micromachanics and Microengineering,2007,17(7):1257-1265.

[16]Innowattech Ltd.,ABRAMOVICH H,HARASH E,et al.Piecoelectric Stack Compression Generator:America,US2011/0291526[P].2011-12-01.

[17]YUAN T C,YANG J,SONG R G,et al.Vibration Energy Harvesting System for Railroad Safety Based on Running Vehicles[J].Smart Materials and Structures,2014,23(12):125046.

[18]袁天辰.基于車輛運行的軌道振動能量回收系統研究 [D].上海:上海工程技術大學,2014.

[19]WANG J J,SHI Z F,XIANG H J,et al.Modeling on Energy Harvesting from a Railway System Using Piezo-electric Transducers[J].Smart Materials and Structures,2014,24(10):105017.

[20]王海燕.車致軌道振動能量俘獲研究[D].北京:北京交通大學,2013.

[21]NELSON C A,PLATT S R,ALBRECHT D,et al.Power Harvesting for Railroad Track Health Monitoring Using Piezoelectric and Inductive Devices[C]//Proceedings of SPIE:Active and Passive Smart Structures and Integrated Systems,2008.

[22]GATTI G,BRENNAN M J,TEHRANI M G,et al.Harvesting Energy from the Vibration of a Passing Train Using a Single-degree-of-freedom Oscillator[J].Mechanical Systems and Signal Processing,2016,66/67:785-792.

[23]WANG J J,PENAMALLI G P,ZUO L.Electromagnetic Energy Harvesting from Train Induced Railway Track Vibrations[C]//Proceedings of IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications.Suzhou:IEEE,2012:29-34.

[24]POURGHODRAT A,NELSON C A,HANSEN S E,et al.Power Harvesting Systems Design for Railroad Safety[J].Journal of Rail and Rapid Transit,2014,228(5):504-521.

[25]POURGHODRAT A.Energy Harvesting Systems Design for Railroad Safety[D].Nebraska:University of Nebraska-Lincoln,2011.

[26]ZHANG X T,ZHANG Z T,PAN H Y,et al.A Portable High-efficiency Electromagnetic Energy Harvesting System Using Supercapacitors for Renewable Energy Applications in Railroads[J].Energy Conversion and Management,2016,118:287-294.

[27]翟婉明.車輛-軌道耦合動力學[M].4版.北京:科學出版社,2015.

[28]International Electrotechincal Commission.International Standard IEC 60068-2-6,Test Fc:Vibration(sinusoidal)[S].Geneva:IEC Publications,2007.

[29]European Committee for Standardization.BS EN 15273-2 Railway Application-Gauges Part 2:Rolling Stock Gauge[S].Brussels:European Committee for Standardization,2014.