高炮弱相關射擊誤差的毀殲概率計算模型

姚志軍， 謝杰濤， 趙志明， 郭治， 王軍

(1.中國白城兵器試驗中心, 吉林 白城 137001; 2.南京理工大學 自動化學院, 江蘇 南京 210094)

0 引言

毀殲概率反映了高炮武器系統的整體性能，是最重要的戰術技術指標之一。計算高炮毀殲概率的方法有實測統計法、模擬統計法和數學描述法。在武器系統定型試驗中，出于安全性和費效比等因素考慮，不可能獲得大量對真實目標的毀殲數據，實測統計法的應用從而失去了統計意義。模擬統計法也稱Monte Carlo方法，其本質是用計算機模擬打靶，通過延長模擬時間和增加計算資源來獲得足夠多的數據，但是其正確性依賴于數據生成模型的正確性，主要用于模型驗證和數據探索，業界尚不能接受用其計算結果作為定型依據。數學描述法通過對射擊誤差和毀殲機理進行分析，試圖推導出毀殲概率的計算表達式，已成為學者們研究重點。

文獻[1-4]和國家軍用標準GJBZ 20499—98“高炮武器系統射擊效率評定”[5]按時間相關性將高炮武器系統的隨機誤差分為強相關誤差、弱相關誤差和不相關誤差3類，并認為這3類誤差是彼此無關的正態過程。用d表示射擊誤差隨機變量的維數(d=2為著發彈藥，d=3為空炸彈藥)，用n表示點射長度，則精確計算高炮點射的毀殲概率需要進行n×d重積分。若只考慮強相關誤差和不相關誤差，則只需要進行2d重積分，由此可見毀殲概率計算的復雜性主要是由弱相關誤差引起的。如何處理弱相關誤差，在保證計算準確性的同時降低計算復雜度，是數學描述法建模的關鍵問題。文獻[1-4]中的誤差平均法、相關系數最小二乘法和經驗公式等誤差模型轉換法均試圖將弱相關誤差分解為強相關部分和不相關部分，并將前者與強相關誤差合并為重復誤差，將后者與不相關誤差合并為不重復誤差，進而給出毀殲概率計算的4重積分表達式。自從誤差模型轉換法中的誤差平均法寫入國家軍用標準GJBZ 20499—98[5]后，這種分解方法幾成定勢，此后相關文獻在涉及此內容時主要沿用結論，但這些方法均無法保持分解前后毀殲概率不變性，也不能給出結果的近似程度，因此長期以來靶場并不直接回答毀殲概率指標。文獻[6]將平穩正態的射擊誤差序列分解為共有分量和非共有分量，將共有分量進一步分解為預測值和預測誤差，雖然仍沿用弱相關分解的思路，但是已經試圖引入現代控制理論的思想解決問題，不過文獻[6]進行公式推導時只考慮了弱相關誤差與初值的相關性，與弱相關誤差狀態方差不符。

本文從射擊學基本假定出發，建立了弱相關誤差序列的狀態方程，采用嚴格的數學演繹，利用遞推關系推導出命中概率的精確計算模型。給出了0-1毀傷定律毀殲概率計算模型，以方便與現有算法的比較。

1 弱相關誤差序列狀態方程

射擊誤差對著發彈藥而言是迎彈面上的二維隨機序列，對空炸彈藥而言是空間三維隨機序列，二者沒有本質區別。本文采用一維形式進行分析，以方便地擴展到二維和三維形式。

記射擊誤差序列為{x(k)∈R;k=1,2,…,n}. 弱相關誤差序列采用平穩正態過程模型進行描述，模型階次由實際數據確定。為了與現行國家軍用標準[5]體制保持一致，本文采用1階平穩正態過程模型，狀態方程如(1)式所示：

(1)

2 命中概率計算

記Ω為命中區域，則高炮n發點射的命中概率為

H(n)=1-P{x(1)?Ω,x(2)?Ω,…,x(n)?Ω}.

(2)

由于各發炮彈之間具有相關性，(2)式對應的計算復雜度為n重積分運算。若要得到滿足精度要求的結果，有必要進一步降低計算復雜度。

2.1 遞推計算模型的推導

用g[x(1)]表示第1發彈目偏差的概率密度函數，則有

(3)

用g[x(k+1)]表示前k發炮彈均脫靶條件下，第k+1發彈目偏差的概率密度函數，f[x(k+1)|x(k)]表示已知第k發彈目偏差條件下第k+1發彈目偏差的概率密度函數，則有

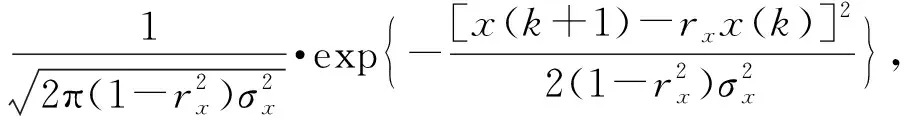
(4)

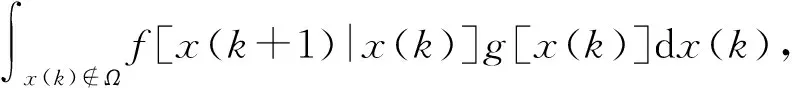
(5)

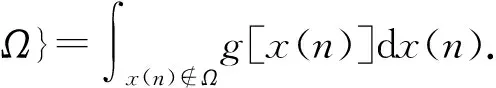
(6)

如圖1所示，將脫靶區域沿坐標軸方向分成l個區域，{i}表示第i個區域。

用Pi(k)表示前k-1發炮彈均脫靶條件下第k發炮彈落在區域{i}的概率，則有

(7)

(8)

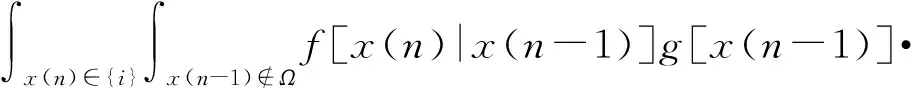
(9)

根據積分中值定理，有

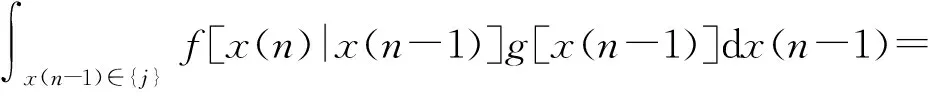
(10)

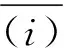
(11)

當‖i‖趨于0時，有

(12)

聯立(8)式～(12)式，有

(13)

聯立(2)式、(6)式、(13)式，有

(14)

分析(14)式可知，這是一個隱含的遞推計算式，且系數與射擊彈藥序號無關。下面將進一步闡述這一結果。

2.2 計算模型的矩陣表示

用Pji(k+1)表示前k-1發炮彈均脫靶情況下第k發炮彈落在區間{j}、第k+1發炮彈落在區間{i}的轉移概率，則有

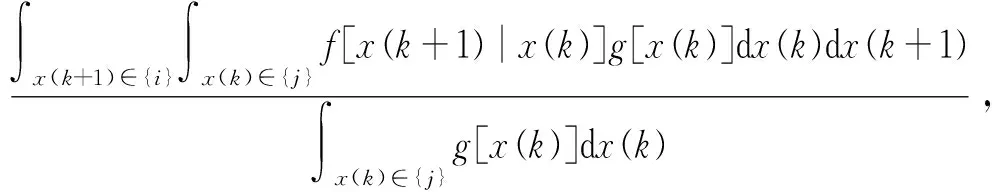
(15)

(16)

當‖i‖、‖j‖均趨于0時，聯立(10)式～(12)式、(15)式，有

(17)

由(17)式可知，Pji(k+1)值與k無關，即Pji(k+1)=Pji，則有

(18)

令

(19)

P(k)=[P1(k),P2(k),…,Pl(k)]T，

(20)

則有

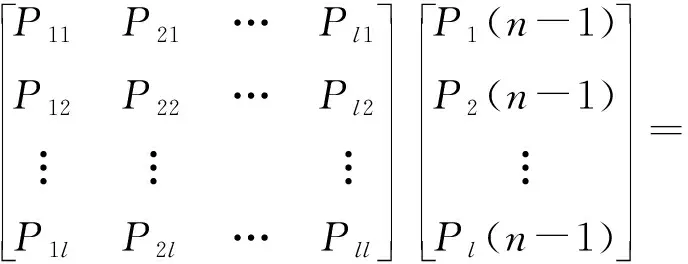
(21)

記l維單位向量e=[1,1,…,1]，有

H(n)=1-eAn-1P(1).

(22)

實際計算時，l只能取有限值。使用(22)式計算命中概率時，計算精度隨著l的增大而提高。因此，可以通過比較增大l前后H(n)的值，確定H(n)的計算誤差。用Hl(n)表示l為有限值時求得的毀殲概率，則H2l(n)對應的計算誤差ΔH2l(n)滿足：

ΔH2l(n)≤|H2l(n)-Hl(n)|.

(23)

(22)式只需要計算l+l2次一維積分，不需要進行n重積分運算。同時可以根據(23)式確定計算精度，滿足了高精度計算的需要。

3 毀殲概率計算

從命中概率到毀殲概率，主要變化是引入了彈藥對目標的毀傷能力，通常用毀傷定律來表征。對著發彈藥而言，使用最廣的是0-1毀傷定律和指數毀傷定律[2]。

0-1毀傷定律代表命中即毀殲，表示為

(24)

指數毀傷定律通常表示為

(25)

式中：ω表示毀殲目標所需的平均命中彈數，它反映了彈藥威力和目標易損性。

指數毀傷定律的基本假定是：各發命中彈對目標毀傷是獨立的，命中彈對目標毀傷沒有累計效應[2]。在此假定下，確定威力的彈藥對確定目標，其毀傷結果是確定且無后效的。如果將目標按易損性劃分，則給定彈藥對具體部位而言，要么能夠毀傷，要么不能毀傷。即只要對目標劃分足夠細致，對具體某個劃分的部位而言ω只有0和1兩種取值，ω>1的部位均可以進行進一步劃分，直至每部分ω的取值非0即1. 因此指數毀傷定律的本質仍舊是0-1毀傷定律。由于本文核心在于闡明毀殲概率遞推模型的數學演繹過程，為了論述的簡潔性，后續均采用0-1毀傷定律。

用Hk+1表示前k發炮彈均不毀殲條件下第k+1發炮彈毀殲概率，則

(26)

H1=1-eP(1)，

(27)

從而有n發炮彈點射的毀殲概率為

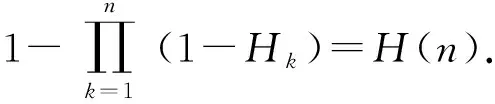
(28)

(28)式表明，對于0-1毀傷定律而言，點射的首次命中概率和毀殲概率是相等的。

4 與現有算法的比較

本文采用1階平穩序列模型作為弱相關誤差隨機狀態方程的基礎，與包含國家軍用標準在內的現有文獻一致[2-5]，也可以采用高階模型。采用0-1毀傷定律是為了比較方便，亦可以擴展到指數毀傷定律和坐標毀傷定律。下面通過計算示例，比較本文遞推法、Monte Carlo法、誤差平均法和相關系數最小二乘法。

Monte Carlo法的計算流程如下：對于每一次模擬實驗，生成n個方差等于弱相關誤差方差的白噪聲；按照(1)式得出弱相關誤差序列，逐發判斷單發炮彈是否命中目標，統計命中彈數；按照(24)式或(25)式計算毀殲概率；重復這種模擬實驗10萬次，取毀殲概率平均值作為Monte Carlo法的計算結果。為了提高計算效率，可以一次生成n×106個方差等于弱相關誤差方差的白噪聲，每次模擬從中選取n個。

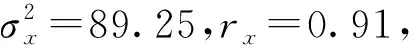
算例1在初始配置基礎上改變rx，得到毀殲概率與相關系數的關系如圖2所示。

從圖2中可以看出，本文遞推法與Monte Carlo法所得曲線幾乎已經重合，從仿真角度佐證了遞推法的正確性。可見誤差平均法、相關系數最小二乘法計算結果偏大。4種算法在rx=1(相當于強相關誤差)時結果一致；在rx=0(相當于不相關誤差)時相差最大，本算例中毀殲概率結果差超過20%.

算例2設置身管數量p=1，重復算例1，得到結果如圖3所示。

綜合算例1和算例2可以看出，誤差平均法和相關系數最小二乘法對于單身管高炮計算結果較為準確，但是仍與遞推法有差距。分析原因可以發現，誤差平均法和相關系數最小二乘法的計算結果有兩部分誤差：一是對弱相關誤差進行近似分解產生的誤差；二是將分解后的誤差分量分別與不相關誤差、強相關誤差合并產生的誤差。對于單身管武器系統而言，這兩種方法都只有近似分解的誤差，在合并部分不產生新的誤差。但是對于多身管高炮而言，這兩部分計算誤差是同時存在的，弱相關誤差近似分解后的不相關部分在同一時刻對于不同身管仍是相同的，而不相關誤差在同一時刻對不同身管是獨立的，相加合并的處理方式增加了不相關誤差的比重，使毀殲概率結果偏大。

算例3在初始配置基礎上設置p×n=24，改變p和n的值，得到毀殲概率與身管數量的關系如圖4所示。

從圖4中可以看出，誤差平均法、相關系數最小二乘法和遞推法的計算結果存在差異，且這種差異隨著身管數量的增加而擴大。在用彈量一定情況下，高炮武器系統的毀殲概率隨著身管數量的增加而下降，由于單身管射擊頻率一定，完成相同用彈量的用時減少，對特定的作戰任務而言，通常要求在保證毀殲概率的前提下用時越短越好，因此武器系統身管數量的確定是毀殲概率和完成任務時間的綜合權衡。

為了突出弱相關誤差這一影響計算復雜度的主要因素，本文算例均忽略了系統均值、強相關誤差和不相關誤差。從計算結果可以看到，現有計算模型進行弱相關誤差分解是有明顯近似的，且這種近似是不可忽略的。

5 結論

本文建立了弱相關射擊誤差的隨機狀態方程，為利用現代控制理論解決射擊學問題創造了條件；構造了連續脫靶條件下弱相關誤差的概率密度函數，推導了命中概率的遞推計算模型；采用0-1毀傷定律推導了毀殲概率的計算模型，其結果是精確的，可以作為現有計算模型的評價基準，亦可以擴展到指數毀傷定律和坐標毀傷定律；通過算例和現有毀傷概率計算方法進行了比較，說明包括國家軍用標準在內的誤差模型轉換法均有明顯偏差。

需要特別指出的是，本文給出的遞推法正確性是在射擊學基本假定前提下用嚴格的數學演繹所保證的，而非與Monte Carlo法一致性證明的，算例中本文方法與Monte Carlo法的高度一致只是本文方法正確性的一個佐證。事實上，在缺乏具有統計意義的實際射擊結果的大前提下，由數學演繹保證正確性的本文方法是評價其他方法的基準。

參考文獻(References)

[1] 潘承泮. 武器系統射擊效力分析[M]. 北京: 國防工業出版社, 1985.

PAN Cheng-pan. Firing efficiency analysis of weapon system[M]. Beijing: National Defense Industry Press, 1985. (in Chinese)

[2] 潘承泮. 武器系統射擊效力[M]. 北京: 兵器工業出版社, 1994.

PAN Cheng-pan. Firing efficiency of weapon system[M]. Beijing: Publishing House of Ordnance Industry, 1994. (in Chinese)

[3] 田棣華, 肖元星, 王向威, 等. 高射武器系統效能分析[M]. 北京: 國防工業出版社, 1991.

TIAN Di-hua, XIAO Yuan-xing, WANG Xiang-wei, et al. Efficiency analysis of anti-aircraft weapon system[M]. Beijing: National Defense Industry Press, 1991. (in Chinese)

[4] 羅興柏, 劉國慶. 陸軍武器系統作戰效能分析[M]. 北京: 國防工業出版社, 2007.

LUO Xing-bai, LIU Guo-qing. Efficiency analysis of land force weapon system[M]. Beijing: National Defense Industry Press, 2007. (in Chinese)

[5] 中國人民解放軍總參謀部炮兵裝備技術研究所. GJBZ 20499—98 高炮武器系統射擊效率評定[S]. 北京: 中國人民解放軍總參謀部, 1998.

Institute of Artillery Equipment Technology, General Staff Department of the Chinese People’s Liberation Army. GJBZ 20499—98 Efficiency assessment of anti-aircraft weapon system[S]. Beijing: General Staff Department of the Chinese People’s Liberation Army, 1998. (in Chinese)

[6] 陶德進, 史慧敏, 王軍, 等. 基于共有分量分解的速射火炮毀傷概率計算模型[J]. 兵工學報, 2012, 33(11) : 1358-1363.

TAO De-jin, SHI Hui-min, WANG Jun, et al. Damage probability calculation model of rapid-fire gun based on common component decomposition[J]. Acta Armamentarii, 2012, 33(11): 1358-1363.(in Chinese)