基于電流觀測器的PMSM反推終端滑模控制
徐小明,趙清江
(新鄉職業技術學院,新鄉 453006)
0 引 言
永磁同步電機(以下簡稱PMSM)具有結構簡單、效率高、轉動慣量較小、過載能力強等優勢,現如今已被大量運用于新能源汽車、高速鐵路、機器人等許多工程領域。常規的PID調節方式已經不能達到高性能的控制需求,于是,對于交流永磁同步電機控制方法的研究具有重要的現實意義[1]。
傳統的PMSM控制系統往往需要至少兩相交流電流傳感器來檢測電流信號,這種獲取電流的方式會額外增加電機的設計成本及電機本體體積,當其中一個電流傳感器產生故障或失效時,所獲取的電流信息將會帶來系統控制的誤差。這將嚴重影響PMSM 在精度和可靠性要求較高的場合中的應用。文獻[2-4]中已經探索了利用單個電流傳感器獲取和重構相電流信息的技術。因此,本文考慮僅在單相電流傳感器可用的情況下,設計了基于單相電流傳感器的PMSM調速系統。
文獻[5]提出了一種采用空間矢量調制控制技術(以下簡稱SVPWM)的三相直接矩陣變換器(以下簡稱DMC)驅動系統中,單電流傳感器交流電機電流重構的方法。該算法將零矢量應用時間分為2個區間,并利用單霍爾電流傳感器在DMC中來測量相電流。通過對三相異步電動機的仿真,驗證了該系統的有效性。但是該方法對電力電子元件的性能提出了考驗。
文獻[6]針對三相電壓型逆變器PMSM調速系統,提出了一種簡單的單電流重構方法,研究了一種具有開關狀態調整方案的空間矢量脈寬調制技術。該方法采用單電流傳感器和嵌入式微系統構成三相永磁同步電動機驅動系統,完成了硬件實現,未對控速系統的動靜態性能進行研究。本文將在單電流傳感器系統的基礎上,進一步分析與研究控制系統的動態性能和魯棒性。
本文研究了一種基于單電流傳感器的PMSM反推終端滑模控制。針對只有一相電流傳感器的PMSM控制系統,設計自適應觀測器實現對另外兩相電流和時變定子電阻的準確估計。將反推控制與終端滑模控制進行結合,研究了一種基于終端滑模負載觀測器的反推控制方法,有效地提高系統的收斂速度,增強系統的魯棒性。利用李雅普諾夫理論證明了系統的穩定性。仿真及實驗結果驗證了該方法的有效性。
1 PMSM數學模型
以表貼式PMSM為控制對象,假定永磁體無阻尼作用且空間磁場分布為正弦分布,不計渦流與磁滯的損耗的情況下,PMSM在d,q坐標系和α,β坐標系下的動態數學模型[7-10]:
(1)
(2)
PMSM機械運動方程:
(3)
電磁轉矩方程:
(4)
式中:ud,uq分別為d,q軸的電壓分量;id,iq分別為d,q軸的電流分量;uα,uβ分別為α,β軸的電壓分量;iα,iβ分別為α,β軸的電流分量;L為定子電感;R為電機定子繞組的電阻;ω為電機的電角速度;ψf為永磁體與定子交鏈磁鏈;Te為電磁轉矩;J為轉動慣量;TL為負載轉矩;B為粘滯系數;p為極對數。
2 自適應電流觀測器設計
假設在PMSM調速系統中,可用的電流傳感器為b相時,根據式(2)α,β坐標系下電流方程,經過Clarke變換可得:
(5)
對式(5)求導可得:
(6)
將式(2)代入式(6)可得:
(7)
設計b相自適應電流觀測器:
(8)
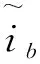
定義誤差變量:
(9)
將式(8)和式(7)作差,可得:
(10)
設計定子電阻自適應律,構造Lyapunov函數:
(11)
式中:r>0。
將(11)求導可得:
(12)
假設式(13)成立:
(13)
這樣,式(12)可改寫:
(14)
由于,在自適應觀測器的采樣時間內,定子電阻的變化基本可以忽略,所以有:
(15)
這樣可以得出:
(16)
因此,由式(13)可得自適應定子電阻方程式:
(17)
因此,定子電阻的估計值就可以有效地趨近于實際值。
為了提高定子電阻的估計精度,確保零穩態誤差,采用PI控制策略進行如下調整:
(18)
式中:Kp,KI分別為比例積分常數。
將定子電阻估計值代入式(2),則自適應觀測器的最終表達式:
(19)
結合式(7)、式(18)和式(19)可以得到設計的自適應觀測器。
3 反推終端滑模控制器的設計
為了提高系統的動態性能,結合反推控制與終端滑模控制各自的優勢,設計基于終端滑模負載觀測器的反推終端滑模控制器[11-14]。
由式(3)、式(4)可得:
(20)
可以得到轉矩觀測器的狀態空間表達式:
(21)
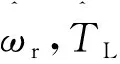
(22)
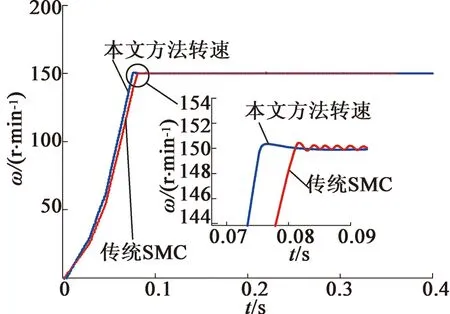
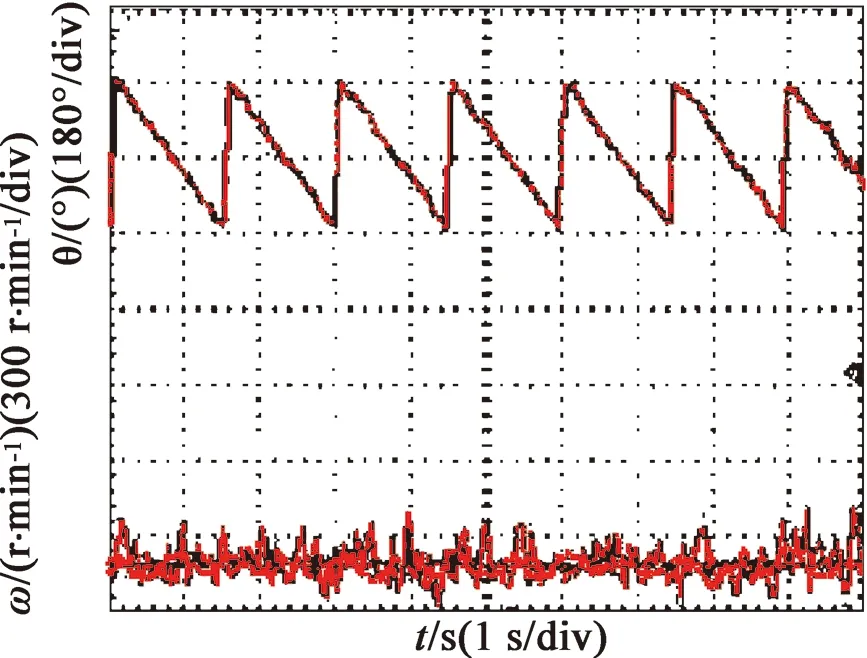
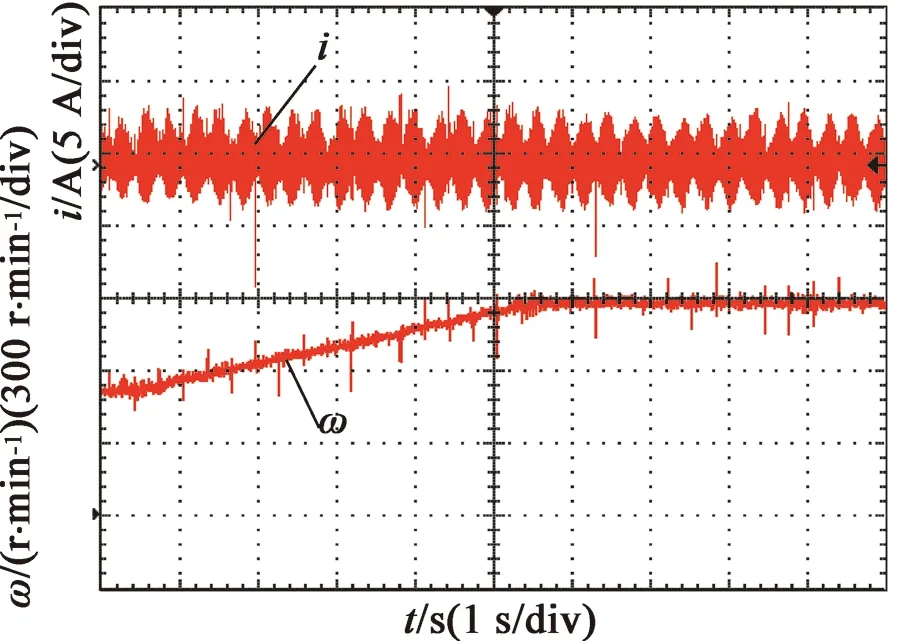
式中:β>0,1 為有效地抑制滑模存在的抖振現象,保證非奇異性,采用一種帶終端吸收引子的趨近方式設計趨近律: (23) 式中:φ1<0,φ2<0,0<γ<1。 (24) (25) 構造Lyapunov函數: (26) 將其微分可得: (27) (28) 式中:r2>0。 結合式(28)和式(27),則: (29) 定義電流的跟蹤誤差: (30) 其微分方程: (31) 選取式(22)為滑模面,設計反推終端滑模速度控制器: 構造PMSM調速系統的Lyapunov函數: (33) 將式(33)微分可得: (34) 結合式(30)、式(31)可得: (36) 式中:rd>0,rq>0。 為了檢驗本文的控制策略的有效性,通過MATLAB/Simulink搭建了系統仿真模型,控制系統仿真及實驗電機的主要參數如表1所示,PMSM調速系統的控制框圖如圖1所示。 表1 PMSM驅動系統的主要參數 圖1 PMSM調速系統的控制框圖 圖2為本文算法與傳統PI滑模控制對比的轉速空載響應曲線。系統初始給定轉速為150 r/min,從圖2可看出,采用本文算法的PMSM調速系統,起動平穩無超調,到達穩態的時間更短。 圖2 空載響應曲線 圖3為系統受到負載擾動時2種控制方法對比曲線。系統在0.2 s時加載2 N·m,在0.3 s時卸載。從圖中可明顯看出,本文控制方法在加載時魯棒性更強。 圖3 擾動時轉速響應曲線 為了進一步驗證本文算法的正確性,搭建PMSM矢量控制系統實驗平臺,實驗是建立在TMS320F2812實時控制系統中進行,實驗結果達到預期效果。 圖4是實測的轉子位置曲線。說明本文所采用的估控制方法控制精度高,控制系統性能較好。 圖4 實測轉子位置 圖5為電機空載起動時穩定狀態對應b相電流波形。從圖5可看出,在電機達到穩定運行狀態時,定子電流穩定且正弦度較好。電機轉速能夠在有限時間內平穩到達給定轉速。 圖5 升速時轉速和相電流波形 本文在單電流傳感器的PMSM調速系統基礎上,設計自適應觀測器實現對另外兩相電流和時變定子電阻的準確估計。將反推控制與終端滑模控制進行結合,研究了一種基于終端滑模負載觀測器的反推控制方法。仿真及實驗結果驗證了本文的控制策略能夠有效地提高系統的收斂速度,增強系統的魯棒性。 [1] 邵偉,李曉寧,董明.永磁同步電機伺服系統控制策略綜述[J].電氣自動化,2013,35(1):1-3,16. [2] GREEN T C,WILLIAMS B W.Derivation of motor line-current waveforms from the DC-link current of an inverter[J].IEE Proceedings B-Electric Power Applications, 1989,136(4):196-204. [3] BLAABJERG F,PEDERSEN J K.An ideal PWM-VSl inverter using only one current sensor in the DC-link[C]//International Conference on Power Electronics and Variable-Speed Drives.IET, London, 1994:458-464. [4] JOO H G,KIM C G,SHIN H B,et al.Detection of three phase currents in space-vector PWM inverters with only one DC link current sensor[C]//International Conference on Industrial Electronics. Control, and instrumentation,IEEE,Taipei, 1996:127-132. [5] METIDJI B,TAIB N,BAGHLI L.Phase current reconstruction using a single current sensor of three-phase AC motors fed by SVM-controlled direct matrix converters[J].IEEE Transactions Industrial Electronics,2013,60(12)5497-5505,. [6] WANG C M,LIN S K.A simple single shunt current reconstruction approach for low-cost permanent magnet synchronous motor drives[C]//Proceedings of 2015 International Automatic Control Conference (CACS).IEEE, 2015:79-84. [7] YANG J.Sliding-mode control for systems with mismatched uncertainties via a visturbance observer [J].IEEE Transactions on Industrial Electronics 2013, 60(1): 4398-4407. [8] YANG J, LIU H, LI S et al.Nonlinear disturbance observer based robust tracking control for a PMSM drive subject to mismatched uncertainties[C]//Control Conference.IEEE,2012:830-835. [9] 肖海峰,劉海龍,賀昱曜. PMSM的線性-滑模變結構直接轉矩控制研究[J].電氣傳動,2014(5):35-39. [10] HAN Y,LI P,ZHENG Z Q.Sliding-mode and back-stepping control for output tracking systems with unmatched uncertainties via a disturbance observer[C]//International Workshop on Variable Structure Systems.VSS,Nanjing,2016:308-311. [11] 佘致廷,董旺華.基于反步滑模變結構的PMSM速度控制[J].控制工程,2016,23(S0):2-5. [12] 韓京清.自抗擾控制器及其應用[J].控制與決策,1998,13(1):19-23. [13] 夏長亮,劉均華.基于擴張狀態觀測器的永磁無刷直流電機滑模變結構控制[J].中國電機工程學報,2006,26(20):139-143. [14] 陳強,南余榮,邢科新.基于擴張狀態觀測器的永磁同步電機混沌系統自適應滑模控制[J].物理學報,2014,63(22):113-120.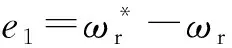
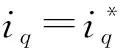
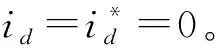
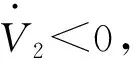
4 仿真及實驗驗證



5 結 語

