多電壓矢量的永磁同步電機模型預測控制

孫斌煌，羅 響，姜淑忠，趙繼敏

(上海交通大學，上海 200240)

0 引 言

模型預測控制(以下簡稱MPC)是一種新型的控制算法。該控制方法思想簡單，以計算機高效的計算能力取代傳統的PI控制器和滯環比較器，無需調節PI和查開關表，對電流有較好的跟蹤效果[3]。文獻[4]比較了電流滯環、脈寬調制和模型預測3種控制策略，驗證了MPC在電機控制上的有效性。文獻[5]提出了一種快速選擇矢量的方法，有效降低了模型預測的計算量和復雜度。魯棒電流控制算法[6]、二矢量的MPC[7]，減小了預測誤差，提高了電機控制的精度。

傳統的控制方式是通過切換兩電平電壓源型逆變器的開關，改變電機的三相導通狀態，利用6個有效電壓矢量和2個零矢量實現電機控制。為進一步提高控制精度，本文通過調整逆變器的開關切換狀態，把兩相導通和三相導通相結合，使其能夠輸出12種非零電壓矢量，研究了一種多電壓矢量的永磁同步電機MPC策略，替代了磁場定向控制的電流環PI控制器。該控制策略對電壓矢量進行了細分，相比于DTC在電壓矢量選擇上更為精確，因此具有較快的響應速度；同時使定子電流更接近正弦波，減小了定子電流諧波畸變率和磁鏈脈動，獲得了良好的控制效果。最后，運用MATLAB/Simulink軟件對不同的控制方法進行仿真比較，驗證了本文控制策略的優越性，并對控制目標函數中權重系數的選擇做了分析。

1 永磁同步電機MPC策略

1.1 永磁同步電機模型

永磁同步電機在d-q旋轉坐標系下的電壓和轉矩方程分別為式(1)和式(2)：

(1)

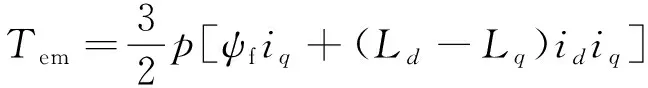
(2)

式中：ud,uq分別為定子直、交軸電壓；id,iq分別為定子直、交軸電流；Ld,Lq分別為定子直、交軸電感，表貼式永磁同步電機可認為Ld=Lq；R為定子電阻；ωe為轉子電角速度；ψf為永磁體磁鏈；Tem為電磁轉矩;p為電機的極對數。

電機機械運動方程：

(3)

式中：J為系統轉動慣量；B為轉子粘滯摩擦系數；TL為負載轉矩。

方案二：L298N 是一款具有高電壓和大電流的全橋驅動IC，可用來驅動兩個直流電機或雙極步進電機4.5～46V 時可提供2A 額定電流，具有過熱時自動關斷和電流反饋檢測功能，安全可靠；可以直接連接到MCU 的IO 口進行控制；并且具有使能端，方便調節PWM 進行速度控制。L298N 芯片可以驅動兩個直流電機[6]，剛好符合我們的驅動要求。

1.2 MPC原理

本文的永磁同步電機模型預測原理如圖1所示。在每一個采樣周期內，通過傳感器測量得到電機三相定子電流和轉速，利用Clarke變換和Park變換，將三相電流變換為交、直軸電流值，在預測模型中計算每種開關狀態下所對應的電流預測值，再根據交、直軸電流給定值由控制目標函數判斷出此次采樣周期內最佳的電壓矢量，并把最佳的控制信號傳送到電壓源型逆變器控制開關管的導通和關斷，以驅動電機正常運行。圖1中虛線方框部分為模型預測的控制過程。

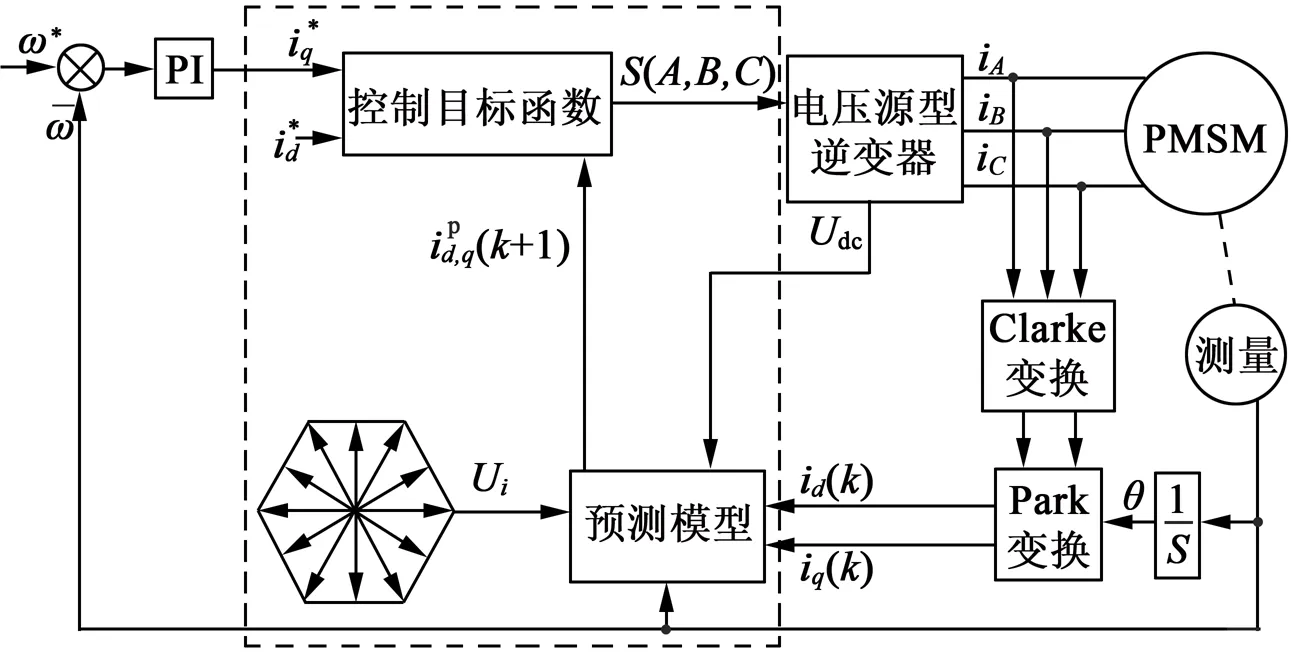
圖1 永磁同步電機MPC系統框圖

1.3 電流預測模型

控制策略的關鍵是對永磁同步電機的交、直軸電流進行準確預測。因此把電機的定子電流作為狀態變量，由式(1)中的電壓方程得到永磁同步電機的電流狀態方程：

(4)

在實際應用中采樣得到的信號是離散的，式(4)中的微分形式難以計算，故必須對狀態方程進行離散化處理。采用一階歐拉法存在較大誤差，為提高交、直電流預測精度，本文采用二階歐拉法對式(4)離散化并進行預測估計。過程如下：

(5)

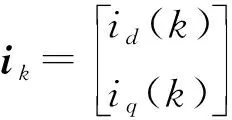
電機轉速的變化是連續的，當采樣周期足夠小或電機轉速穩定時，可認為電機的電角速度ωe在一個采樣周期內保持不變，由式(4)和式(5)可以得到永磁同步電機的電流預測模型方程如下：

式中：E為單位矩陣。

1.4 多電壓矢量MPC

電壓源型逆變器如圖2所示。傳統的逆變器控制方式是上下橋臂各有一個開關導通或關斷，輸出8種電壓矢量(6個非零矢量和2個零矢量)對電機進行控制。當僅有一個橋臂的上橋臂導通，另一個橋臂的下橋臂導通，第三個橋臂全關斷時，又可以形成6個與之前電壓矢量不同的矢量。為了更精確地選擇電壓矢量，實現電機快速起動，減小電流諧波，通過對開關管的導通狀態進行組合，采用14個電壓矢量(12個非零矢量和2個零矢量)的控制策略，使電機在三相導通和兩相導通的交替狀態中正常工作。

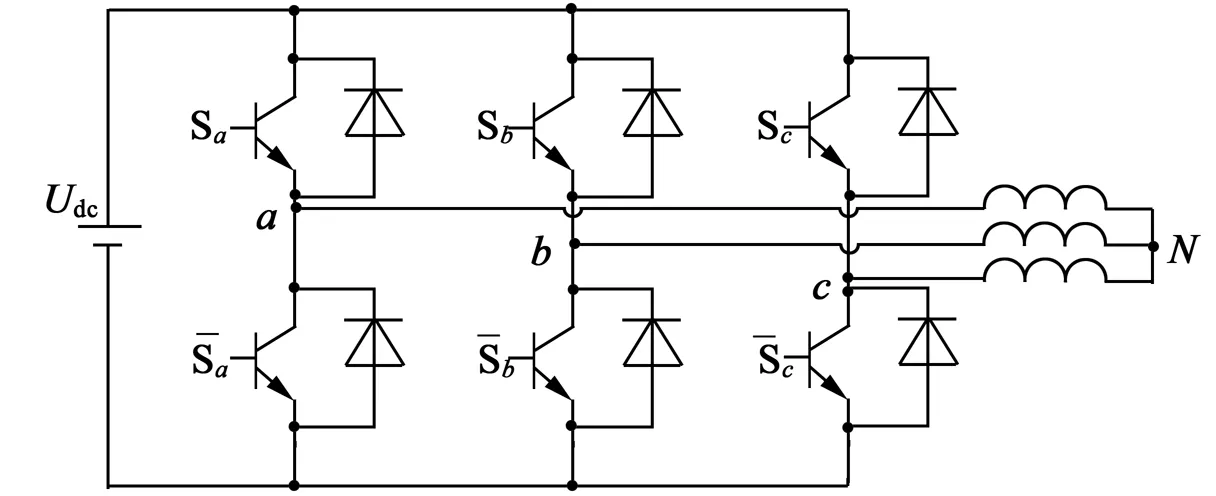
圖2 電壓源型逆變器

根據逆變器的開關導通狀態和直流母線電壓值，分析14種開關狀態下永磁同步電機的電路圖，可以得到不同開關狀態下a，b，c三相對應中性點的相電壓如表1所示。其中，Sa,b,c=1表示上橋臂導通，Sa,b,c=0表示下橋臂導通，Sa,b,c=*表示上下橋臂都關斷。該控制方式比傳統的控制方式多了一個電平選擇。

表1 不同開關下各相對應中性點電壓

由表1各種開關狀態所對應的a,b,c三相的相電壓，利用電壓矢量合成式(7)，可以得到每種開關狀態下的電壓合成矢量如圖3所示。可知,三相導通時的電壓合成矢量與兩相導通時的電壓合成矢量在空間上相差30°電角度，使電壓矢量進一步細分。

(7)

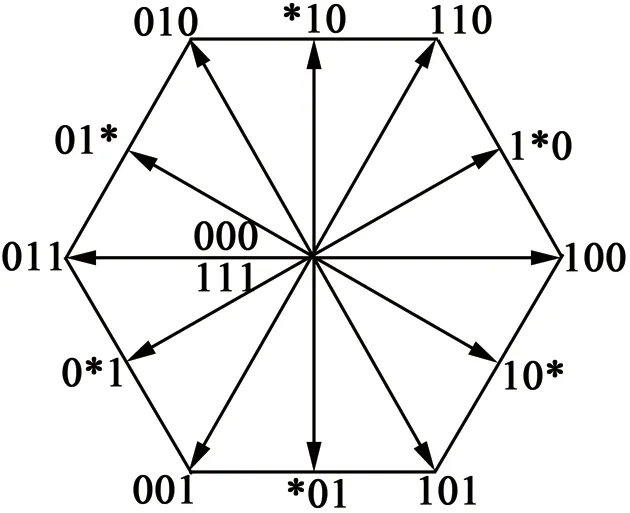
圖3 14個電壓矢量

1.5 控制目標函數

控制目標函數的作用是對每一種電壓矢量所產生的電流預測結果進行評估，最終選出一個最佳的電壓矢量作用于采樣周期，使系統的輸出電流值跟蹤給定值，并限制電流的幅值。在對永磁同步電機的電流進行模型預測時，就是實現id接近零，iq快速跟蹤交軸電流給定值，本文采用式(8)的控制目標函數，當控制目標函數的值為最小時，所對應的電壓矢量為本周期內最佳的電壓矢量。

式中：μ,λ分別為直、交軸電流預測偏差的加權系數，不同的系數選取影響逆變器的開關頻率和定子電流波形。

電流限幅函數：

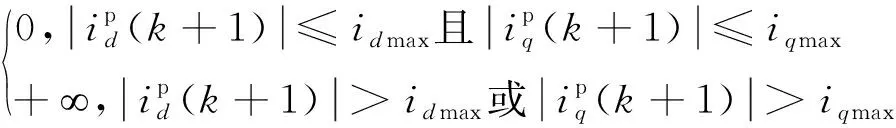
(9)

式中：idmax,iqmax分別為直、交軸電流允許的最大幅值。

2 仿真分析

為了進一步驗證多電壓矢量的永磁同步電機MPC具有較快的響應速度、較小的電流和磁鏈脈動，并分析直、交軸電流預測偏差的加權系數對電機控制的影響。用MATLAB/Simulink搭建了仿真平臺，逆變器母線電壓為310 V，電流限幅為10 A，負載轉矩TL=3 N·m。永磁同步電機參數如下：極對數p=2，直交軸電感Ld=Lq=8 mH，定子電阻R=2.8 Ω,永磁體磁通ψf=0.175 Wb，粘滯摩擦系數B=1.5×10-5，轉動慣量J=0.8×10-3kg·m2。

2.1 FOC、DTC和MPC的比較

初始給定速度1 000 r/min，在t=0.15 s時給定速度變為500 r/min，保持3種控制方式的開關頻率在同一水平，仿真得到FOC、DTC和本文控制方式的速度響應如圖4所示。由于本文MPC對電壓矢量進行了細分，相比于DTC在對矢量的選擇上更加精確，且消除了FOC電流環PI調節的滯后性，因此在起動和減速過程中，多電壓矢量的MPC響應速度遠快于FOC，略快于DTC。

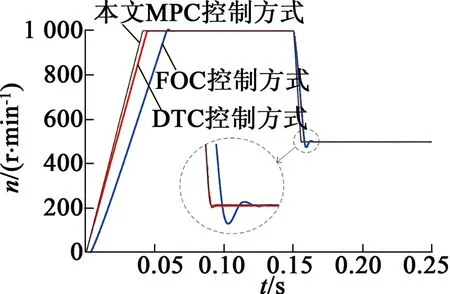
圖4 FOC、DTC和MPC轉速響應比較

當轉速穩定在1 000 r/min時，開關頻率保持在相同水平，得到3種控制方式在同一時間段內的定子電流波形和磁鏈軌跡分別如圖5、圖6所示。比較發現FOC具有較好的電流波形和磁鏈軌跡，本文控制方式的定子電流和磁鏈的脈動比DTC小，電流波形更接近正弦波，磁鏈軌跡更接近圓。利用Simulink對圖中電流波形進行諧波分析，得到FOC、DTC和MPC的電流諧波畸變率(THD)分別為3.61%、12.24%和5.99%，說明本文MPC在控制精度上略低于FOC，但相比于DTC具有較好的電流波形和磁鏈軌跡。

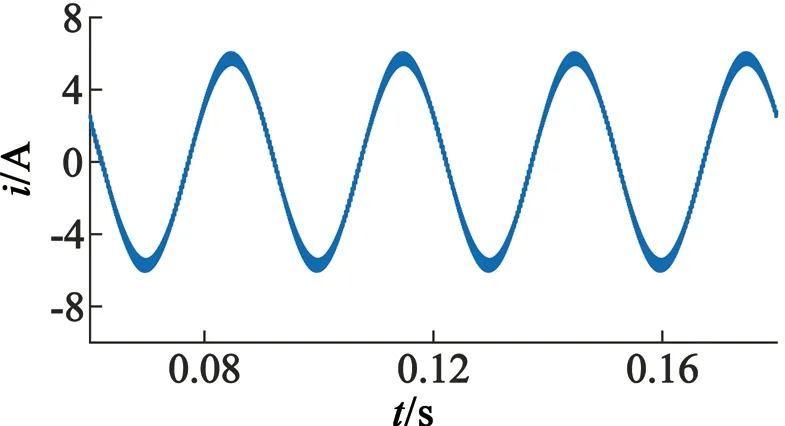
(a) FOC系統

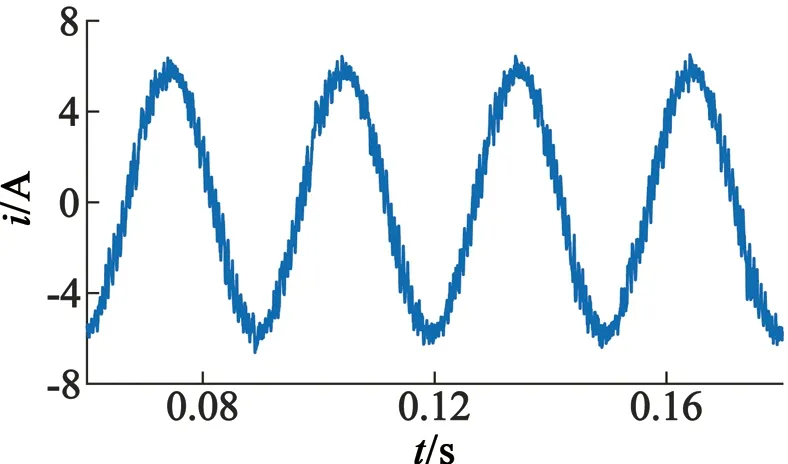
(b) DTC系統

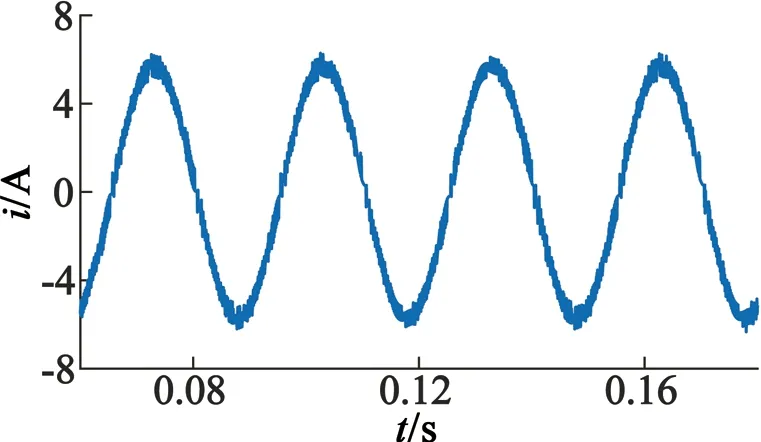
(c) MPC系統

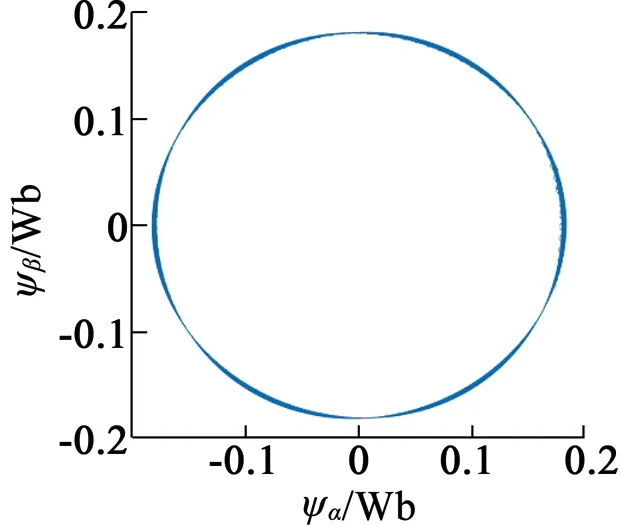
(a) FOC系統

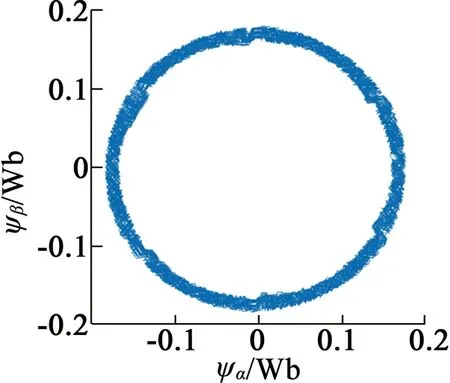
(b) DTC系統

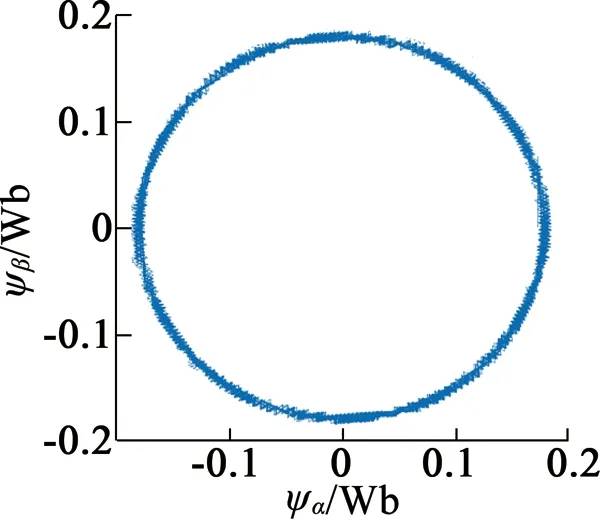
(c) MPC系統

2.2 權重系數對控制策略的影響

為研究控制目標函數中λ和μ的比值對開關頻率fK和電流諧波畸變率THD的影響，系統采樣 頻率為20 kHz，選取不同的λ/μ比值，當轉速穩定在1 000 r/min時得到不同比值下的開關頻率和電流諧波畸變率如表2所示。由表2可知,隨著λ/μ值的增大，開關頻率逐漸升高，最終受限于采樣頻率而趨于穩定；所對應的電流諧波畸變率先緩慢降低后逐漸升高，當λ/μ的值急劇增大時電流諧波成分大幅增加。當λ/μ的值小于0.2以后，電機轉速將出現明顯脈動甚至跟不上給定速度。分析表明，交、直軸電流預測偏差值的權重系數較為接近時，能夠獲得較好的控制效果。

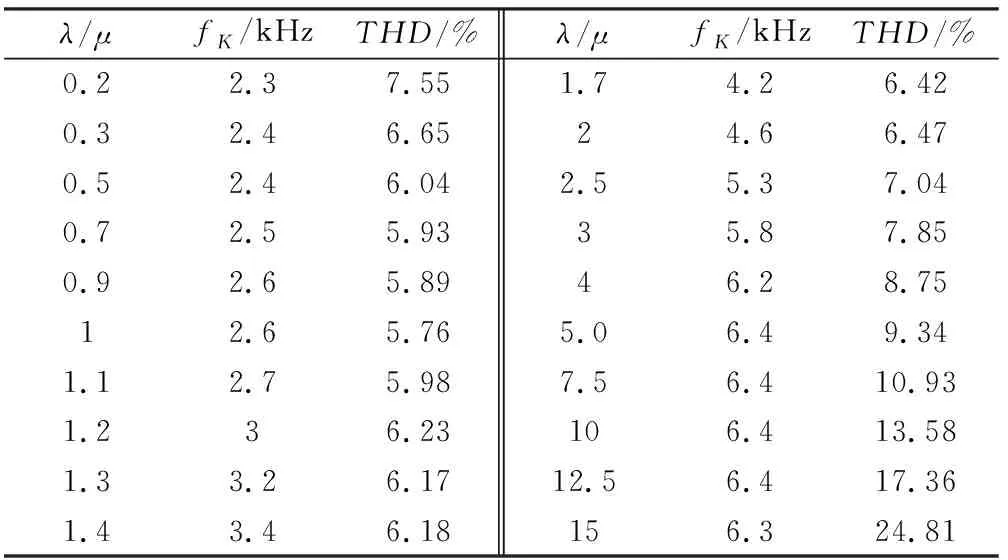
表2 權重系數對fK和THD的影響

3 結 語

本文以預測模型取代FOC的電流環PI控制器，通過改變逆變器的開關狀態，使永磁同步電機在三相導通和兩相導通交替的情況下正常工作，研究了一種多電壓矢量的永磁同步電機MPC。仿真結果和分析表明本文的控制方式響應速度快，定子電流諧波成分少，磁鏈脈動小，相比于傳統的FOC和DTC具有優越性。當控制目標函數中直、交軸電流偏差的權重系數接近時，能夠取得較好的控制效果。

[1] 郝曉弘,魏祥林.永磁同步電機FOC與DTC控制策略原理和仿真的比較[J].科學技術與工程, 2008(13):3463-3469.

[2] 林偉杰.永磁同步電機兩種磁場定向控制策略的比較[J].電力電子技術,2007(1):26-28.

[3] FUENTES E,RODRIGUEZ J,SILVA C,et al.Speed control of a permanent magnet synchronous motor using predictive current control[C]//Power Electronics and Motion Control Conference,Wuhan,China,IEEE,2009：390-395.

[4] RODRIGUEZ J,PONTT J,SILVA C,et al.Predictive current control of a voltage source inverter[J].IEEE Transactions on Industrial Electronics,2007(54):495-503.

[5] 張永昌,楊海濤,魏香龍.基于快速矢量選擇的永磁同步電機模型預測控制[J].電工技術報,2016(6):66-73.

[6] 牛里,楊明,劉可述,等.永磁同步電機電流預測控制算法[J].中國電機工程學報,2012(6):131-137.

[7] 魏香龍.基于模型預測控制的永磁同步電機控制研究[D].北京：北方工業大學,2014.