基于數值分析的船舶斜航運動水動力研究

廉靜靜，楊 曉，尹 勇

(1.大連海事大學 航海學院，遼寧 大連 116026； 2. 大連海事大學 航海動態仿真和控制實驗室，遼寧 大連 116026)

0 引 言

船舶操縱性能與船舶航行的安全性緊密相關，為了提高船舶的航行安全，負責海事安全的國際海事組織IMO(International Maritime Organization)于1993年頒布實施了InterimStandardsforShipManeuverability[1]以及2002年通過了StandardsforShipManeuverability[2]，這使得船舶的操縱性能越來越受到關注和重視。近年來，由于采用數值計算方法能夠提供船體和螺旋槳葉面周圍獨特的定性和定量流場信息，它已成為求取船舶操縱性水動力導數主流方法之一，可將取得船舶操縱性水動力導數代入船舶操縱運動方程，對船舶的操縱性實現預報，同時，采用數值計算方法也逐步成為船模實驗方法的主要輔助手段。

利用計算流體動力學(computational fluid dynamics，CFD)方法研究船舶水動力性能，國內外學者均開展了相關研究工作 ， B. J. GUO等[3]研究了在頂浪中KVLCC2船舶運動的附加阻力；Y. T. JIN等[4]考慮了船舶尺度大小對KVLCC2船舶水動力系數的影響；田喜民等[5]，劉晗等[6]對KVLCC2不同漂角的斜航運動進行了模擬，但這些研究對船體周圍漩渦流場分布情況并未關注，且船體周圍漩渦對船體的阻力、噪聲密切相關，從而對船舶操縱性產生影響。筆者選用國際操縱性標準船型KVLCC2為研究對象，采用ANSYS FLUENT 14.5軟件對該船模的斜航運動的黏性流場進行了數值模擬，對黏性流場中數值模擬中的計算網格、湍流模型等關鍵技術問題進行了深入研究，獲得作用在船舶上的縱向水動力、橫向水動力、艏搖力矩，并將計算的數值結果與日本海上技術安全研究所(National Maritime Research Institute，NMRI)實驗結果進行比較分析，同時采用最小二乘法進行曲線擬合，求得船舶操縱水動力導數，采用Q準則獲得了船舶周圍的漩渦流場。

1 數學模型

1.1 控制方程

求解各種計算模型流場及流體動力所采用的基本方法是RANS方法[7]，其RANS方程的形式如下：

(1)

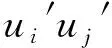
1.2 湍流模型

分析比較了幾種湍流模型的適用性，筆者選用的湍流模型為重整化群RNG(Renormalization Group)κ-ε模型，與求解高雷諾數的標準Standard κ-ε湍流模型相比，重整化群RNG κ-ε湍流模型考慮了低雷諾數的影響，通過在大尺度運動和修正后的湍流黏度項體現了小尺度的影響，使得在平均流動中的旋轉及漩流流動情況得以處理，同時，在重整化群RNG κ-ε模型中引入時均應變率Eij，從而使得高應變率和流線彎曲程度較大的流動該模型能夠更好地處理。該模型由V. YAKHOT等[8]于1986年提出的。該湍流模型是通過重整化數學方法推導出瞬時的NS方程，重整化群RNG κ-ε模型方程[9]為

ρε-YM+Sκ

(2)

(3)

1.3 Q準則

Q準則是由J. C. R. HUNT等[10]提出的，通過使用正值Q來作為流場漩渦的識別方法，當Q值為正時，說明該流場區域內的流體微元以旋轉運動為主導，當Q值為負時，則說明該流場區域內的流體微元的旋轉運動較弱。定義流場中速度梯度張量的第二矩陣不變量Q可表達為

(4)

式中：Wij為速度梯度張量的旋轉率張量，代表純粹旋轉運動；Sij為速度梯度張量應變率張量。

2 數值計算

筆者研究對象為國際標準船型KVLCC2油輪，船舶模型如圖1，其船模的主要參數如表1。

圖1 KVLCC2 船模Fig. 1 KVLCC2 ship model

m

首先構建計算域的幾何模型，即求解計算時的離散積分空間，依據船舶斜航運動的物理問題，確定計算域的大小。計算域如圖2(以下船長記為L)，距離船首1.5L設置為上游邊界，距離船尾3L設置為下游邊界，向下距離1.5L處設置為水深方向，左右兩側方向為1.5L。只有根據物理條件，給出合理的邊界條件，才能獲得流場的正確解，上游邊界是速度進口邊界，船舶航速是0.994 m/s，對應的Froude數為0.142 4，為低速船，自由面興波影響較小，故采用“疊模”模型，將自由面視為對稱邊界，船舶的兩側和計算域的底面視為無滑移壁面邊界條件，船體看作無滑移壁面邊界條件，下游邊界看作出流outflow邊界。

圖2 計算域Fig. 2 Computational domain

采用有限體積法對微分方程進行離散時，需要將控制方程在空間區域上進行離散，隨后求解得到離散方程組，需要生成網格將控制方程在空間區域上進行離散，且網格質量和數量直接影響計算精度與計算速度，可通過前處理軟件ICEM CFD對整個計算域進行網格劃分，如圖3船舶表面網格。在整個網格劃分過程中，盡量使用結構網格以減少網格數量，提高計算速度，在船舶球鼻首和船舶尾部的地方采用結構網格比較困難，可以利用非結構網格進行劃分，網格生成方法采用自上而下的方法，船舶首尾部曲率大的線條部分線網格加密尺寸小，使得該部分網格較為密集，相比之下，船舶首尾部和舭部面網格加密尺寸較大，以便減少整個計算域內網格數量。當處理近壁面流動時，邊界層內的位置通常用無量綱形式y+來表示，y+是以垂直于壁面的距離為長度尺度，即為第一個網格點到壁面距離，此處將邊界層棱柱網格y+可設置為30，整個計算域網格總數為70萬左右，圖4為整個計算域的網格劃分遠觀圖。為提高計算效率，計算域內網格數量不能過多，但考慮精度，某些區域的網格數量還需加密，主要依據計算時耗時和計算的精度，從兩者中折中確定網格數量。采用壓力耦合方程組的半隱式SIMPLE算法求解連續方程中建立的壓力修正方程，得到壓力場的修正值，利用壓力修正值更新速度場和壓力場，不收斂時重復迭代，最終得到壓力場和速度場的收斂解，為了保證計算過程中空間離散不發散，在初始階段，采用一階迎風格式離散動量、湍流動能和湍流耗散率等參數，待計算穩定后采用二階迎風格式即可，這樣即可以保證穩定性又提高準確性，同時，為保證計算的收斂性，改變亞松弛因子。

圖3 船舶體表網格Fig. 3 Ship hull surface mesh

3 結果與分析

筆者計算了KVLCC2斜航船模漂角分別為0°、3°、6°、9°和12°時的縱向力系數、橫向力系數和艏搖力矩系數，如圖5，并將計算得到的結果與日本NMRI獲得的試驗結果[11]進行對比，從圖5中可以看出，實驗結果吻合較好，漂角較小時，數值計算的船舶的橫向力系數與試驗結果比較誤差約為6%左右，在整個計算過程中，船舶縱向力系數與試驗結果誤差較大，約為12%左右，誤差與離散時間步長、離散方法和網格疏密等因素有關，湍流動能值和湍流耗散值會對橫向阻力系數和縱向阻力系數產生影響，選擇合適的湍流動能值和湍流耗散值是非常重要的。

圖5 縱向力系數、橫向力系數及艏搖力矩系數Fig. 5 Longitudinal force coefficientlateral force coefficient and yaw moment coefficient

根據最小二乘法原理進行曲線擬合，求得船舶水動力導數，如表2，圖6為不同側向速度下水動力導數的曲線擬合結果。

表2 船舶水動力導數Table 2 Ship hydrodynamic derivatives

圖曲線和曲線擬合Fig. curve and curve fitting

將漂角為12°時船體艏部和尾部表面壓力系數分布與日本NMRI[12]實驗數據進行比較如圖7。從圖7中可以看出采用數值計算的結果和實驗數據結果相似，在船首部迎風面所受的壓力較大，背風面所受壓力較小，而船尾則相反。兩者不同之處為，實驗數據在船舶尾部背風面和迎風面壓力系數曲線中某條線出現了閉合，數值模擬并非發現該現象。

圖7 β=12°時船體表面壓力系數分布Fig. 7 Hull pressure coefficient distribution(β=12°)

通常Q準則可觀測到船舶周圍的渦結構，圖8是漂角為0°、3°、6°、9°和12°時船舶周圍的漩渦流場。

圖8 船體周圍的漩渦流場Fig. 8 Vorticity flow distribution around ship

從圖8中可以看出，隨著漂角逐漸增加，船舶周圍的漩渦流場變得更加復雜，尤其是船舶尾部錐形部分和船中部周圍流場高度復雜，這是因為隨著漂角逐漸增加從船舶中部側漩渦越發明顯，逐漸出現分離，這使得漩渦結構得到了充分發展。當漂角為0°時，船舶KVLCC2周圍的漩渦流場受到船首和船尾錐形部分邊界層發展支配。當漂角為12°時，船首舭部漩渦、船首側渦、船尾漩渦、側漩渦逐漸形成，同時，船舶尾部漩渦在迎風面與船舶尾部側渦合并在一起，如圖9，在背風面與船舶尾部發卡渦合并在一起，在船首舭部漩渦看起來有些卡門渦脫落，而船舶首部側漩渦有些螺旋不穩定，產生了一些螺旋波動和螺旋漩渦。

圖9 船尾局部漩渦流場(β=12°)Fig. 9 Vorticity flow distribution around ship stern(β=12°)

4 結 語

通過求解不可壓縮黏性流的RANS方程，結合重整化群RNGκ-ε湍流模型，對KVLCC2船舶斜航運動的黏性流場進行數值模擬，計算不同漂角下船舶所受的縱向水動力、橫向水動力、艏搖力矩，并將其計算獲得的結果與實驗數據相比較，吻合較好，計算結果產生的誤差在允許的范圍內，湍流動能值、湍流耗散值、離散時間步長、離散方法和網格疏密對計算結果有影響，同時采用最小二乘法進行曲線擬合，求得船舶操縱水動力導數，采用Q準則獲得了船舶周圍的漩渦流場，當船舶漂角逐漸增加時，船體周圍

的漩渦越發復雜。采用數值分析的方法求取水動力導數，將計算的結果帶入船舶運動方程中，為船舶CFD實現實用化提供一種有效的思路。

參考文獻(References)：

[1] International Maritime Organization (IMO).ResolutionA. 751(18):InterimStandardsforShipManeuverability[S]. London: IMO, 1993.

[2] International Maritime Organization (IMO).ResolutionMSC.137 (76):StandardsforShipManeuverability[S]. London: IMO, 2002.

[3] GUO B J, STEEN S, DENG G B. Seakeeping prediction of KVLCC2 in head waves with RANS[J].AppliedOceanResearch, 2012, 35:56-67.

[4] JIN Y T, DUFFY J, CHAI S H,et al. URANS study of scale effects on hydrodynamic manoeuving coefficients of KVLCC2[J].OceanEngineering, 2016, 118:93-106.

[5] 田喜民, 鄒早建, 王化明. KVLCC2 船模斜航運動黏性流場及水動力數值計算[J]. 船舶力學, 2010,14(8):834-840.

TIAN Ximin, ZOU Zaojian, WANG Huaming. Computation of the viscous flow and hydrodynamic forces on a KVLCC2 model in oblique motion[J].JournalofShipMechanics,2010,14(8): 834-840.

[6] 劉晗,馬寧,鄧德衡,等. 循環水槽平面運動機構試驗及其斜航試驗的數值模擬[J]. 大連海事大學學報, 2016,42(2):8-13.

LIU Han, MA Ning DENG Deheng ,et al. Planar motion mechanism tests in circulating water channel and numerical simulation of oblique towing[J].JournalofDalianMaritimeUniversity, 2016, 42(2):8-13.

[7] 王福軍.計算流體動力學分析——CFD軟件原理與應用[M].北京:清華大學出版社,2004:7-10.

WANG FuJun.ComputationalFluidDynamicsanalyzer:softwareprincipleandapplication[M].Beijing: Tsinghua University Press, 2004:7-10.

[8] YAKHOT V, ORSZAG S A, PANDA R. Computational test of the renormalization group theory of turbulence[J].JournalofScientificComputing, 1988, 3(2):139-147.

[9] ORSZAG S A, YAKHOT V, FLANNERY W S, et al. Renormalization group modeling and turbulence simulations[C]//InternationalConferenceonNear-WallTurbulentFlows,Tempe,Arizona. Tempe, Arizona:[s.n.], 1993.

[10] HUNT J C R, WRAY A A, MOIN P. Eddies, stream and convergence zones in turbulent flows[C]//StudyingTurbulenceUsingNumericalSimulationDatabases,Proceedingsofthe1988SummerProgram. United States:[s.n.], 1988: 193-208.

[11] JACQUIN E, GUILLERM P E, DROUET A, et al. Simulation of unsteady ship maneuvering using free-surface RANS solver[C]//Proceedingof26thSymposiumonNavalHydrodynamics. Rome,Italy:[s.n.],2006.

[12] KUME K, HASEGAWA J, TSUKADA Y, et al. Measurements of hydrodynamic forces, surface pressure, and wake for obliquely towed tanker model and uncertainty analysis for CFD validation[J].JournalofMarineScienceandTechnology, 2006, 11(2): 65-75.