考慮自動駕駛儀故障的復合全局滑模制導律

陳 峰,何廣軍,熊思宇,何陽光

(空軍工程大學 防空反導學院,陜西 西安 710051)

雷達導引頭在探測和跟蹤低空巡航導彈時,除了低層大氣的不均勻性引起的電波折射效應外,地面或海面產生的鏡面反射或漫散射還會引起多徑效應,從而造成跟蹤誤差,甚至引起脫靶[1-2]。因此,設計超低空目標的攔截彈道應從避免多徑干擾方面突破。束川良、王國勝等人提出可通過設計布儒斯特彈道,使攔截彈以最佳的彈目視線角即布儒斯特角跟蹤攔截目標[2-3],使導引頭受到的多徑干擾最小。文獻[4]通過電磁散射理論的分析得出結論:不同環境的布儒斯特角是不同的,海洋和土壤環境在10°左右,沙漠環境在30°左右。制導律中比例導引律(proportional navigation,PN)應用最為廣泛,并延伸了多種改進形式[5-6],但其用于攔截機動目標時抗干擾性能較差。近年來,滑模制導律因具有良好的魯棒性和抗干擾性能而被很多學者所關注[7]。為了改善系統的收斂特性,相關學者提出了有限時間收斂的終端滑模(terminal sliding mode,TSM)制導律[8-10]。但以上所有的傳統滑模控制方法,系統狀態的運動需經歷2個階段:趨近滑模階段和沿滑模階段。變結構系統的強魯棒性僅體現在沿滑模階段,而在趨近滑模階段,系統的動態特性對參數的攝動和外部的干擾極其敏感。攔截超低空目標時,地海雜波和多徑效應會加強參數的攝動和外部的擾動,因此,為了提高攔截的精度,有必要設計一種具有全程魯棒性的制導律。隨著導彈一體化設計的發展,又有學者研究了考慮導彈自動駕駛儀延遲特性的制導律設計[11-14],但是并沒有考慮復雜電磁環境下,自動駕駛儀執行制導指令時可能發生的故障問題。

本文基于全局滑模控制的原理,設計了一種具有全程魯棒性的全局滑模(global sliding mode,GSM)制導律。該制導律可確保在跟蹤攔截低空目標的過程中,將彈目視線角約束至環境所對應的布儒斯特角。同時,可使系統狀態省去趨近滑模運動的階段,直接進入沿滑模運動的階段,從而使系統的全過程具有強魯棒性。針對復雜環境中自動駕駛儀執行制導指令時可能發生的故障問題,設計了一種虛擬指令作為故障擾動的補償。結合虛擬指令設計出的復合全局滑模(composite global sliding mode,CGSM)制導律大大提高了系統的抗干擾性能,提高了超低空攔截的精度。

1 彈目相對運動模型

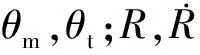
假設攔截彈與目標的速度大小為常值,可得彈目相對運動方程為

(1)

(2)

(3)

(4)

對式(1)和式(2)分別求導可得:

(5)

(6)

式中:at,R=atsinηt,am,R=amsinηm,at,q=atcosηt,am,q=amcosηm。

選取狀態變量為

(7)

根據所取狀態變量和式(6),可得狀態方程為

(8)

2 全局滑模(GSM)制導律的設計

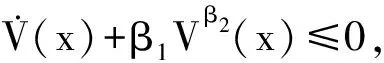
式中:V(x0)為V(x)的初值。

導彈在終端攻擊超低空目標時,為了避免多徑干擾對制導精度的影響,視線角需穩定在環境所對應的布儒斯特角附近,因此可定義跟蹤誤差為

er=q-qd

(9)

式中:qd為布儒斯特角。

同時,為了提高系統對參數攝動和多徑干擾的抗干擾性能,需設計具有全程魯棒性的制導律,為此,可構造全局滑模面為

(10)

h>0,動態函數m(t)需滿足3個條件:

②t→∞,m(t)→0;

③m(t)具有一階導數。

條件①可保證當t=0時,S(0)=0,從而保證所設計的全局滑模面通過系統的任意初始狀態,消除滑模控制中的趨近模態,使系統具有全程魯棒性,提高對外部干擾和參數攝動的抗干擾性能;條件②是為了保證所設計的動態非線性滑模面最終演化為線性滑模面,提高系統的響應速度;條件③是為了保證所設計滑模面的連續性。為此,可設計動態函數為

m(t)=m(0)e-γt

(11)

為了達到期望的收斂特性,可構造全局滑模的趨近律為

(12)

式中:常數ε>0,常數k>0。

對式(10)求導,并聯立式(12),可得:

(13)

聯立式(8)和式(13),求得GSM制導律為

(14)

定理1制導律(14)可保證系統(8)將彈目視線角收斂至期望的布儒斯特角。

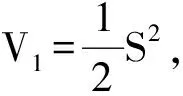
(15)

(16)

由式(16)可知,系統狀態省去了趨向滑模面運動的過程,說明系統的初始狀態已經位于滑模面上了,直接進入滑動模態,從而具有全程魯棒性。

系統到達滑模面,沿滑模面運動時,有:

(17)

因為t→∞,m(t)→0,此時,由Lyapunov穩定性理論可得,系統的狀態能收斂至平衡點er=0,即系統能將彈目視線角收斂至期望的布儒斯特角。

證畢。

3 自動駕駛儀故障補償

在復雜的物理環境下,導彈自動駕駛儀在執行制導系統傳過來的理想制導指令am時,執行機構、計算機等硬件設備可能會發生故障,導致實際執行的指令相對于理想的制導指令會出現偏差損失,同時系統內部可能還存在著機械摩擦擾動,此時的式(8)可表示為

(18)

式中:f為自動駕駛儀的故障損失系數,E為額外的附加擾動,且滿足0<ξ≤f<1,|E|≤K,K為一個正的常數,ξ為很小的正常數。

為了補償自動駕駛儀故障的影響,設計了如下的虛擬補償制導指令:

amf=sgn(S)sgn(cos(q-θm))(αK+β|amn|)

(19)

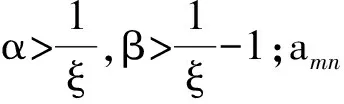
amc=amn+amf

(20)

定理2選取式(10)所示的滑模面切換函數,則式(20)所示的復合制導律可以補償自動駕駛儀故障帶來的影響,確保攔截彈以期望的視線角攔截目標。

證明構造Lyapunov函數為

(21)

對Lyapunov函數V2求導,結合式(15),可得:

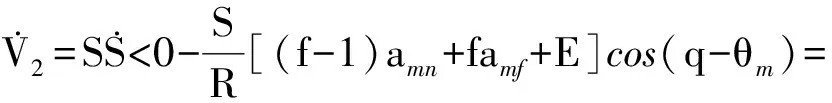
(22)

證畢。

式(14)和式(20)所示的制導律中,由于不連續開關項的存在,會使滑動模態出現抖振現象。可采用高增益連續函數Θ(S)=S/(|S|+σ)代替符號函數,用以消除抖振的影響[16],其中σ為很小的正常數,代表所設計的連續化函數接近sgn(S)的程度。

4 算例分析

1)GSM制導律的有效性驗證(仿真1)。

為了驗證式(14)所設計的GSM制導律對超低空目標攔截的適用性,在沙漠環境下,對超低空機動目標進行攔截仿真驗證,并將其與比例(PN)導引律進行比較。

PN導引律設計為

(23)

設低空目標的初始飛行高度為yt0=10 m,初始位置為xt0=7 800 m,初始飛行速度為vt0=200 m/s,初始彈道傾角θt0=180°,目標機動加速度為at=-20sin(0.5πt);攔截彈的初始水平位置為xm0=0,高度為ym0=3 500 m,初始速度vm0=400 m/s,初始彈道傾角θm0=-45°。由前面已知,沙漠環境的布儒斯特角在30°左右(這里只是表示角度的大小,按照圖1注標的方向應為負值)。GSM制導律參數設置為h=2,k=30,ε=120,σ=0.01,γ=0.5;PN導引律參數設置為N=3。由于彈體物理結構的限制,假設攔截彈最大加速度響應為20g。

由圖2和圖3可知,GSM與PN兩種制導律雖然都能保證攔截彈對低空目標進行攔截,但是PN在跟蹤攔截低空目標的過程中,無法將彈目視線角約束至期望的布儒斯特角附近。且由圖4可知,GSM在終端攻擊目標時,能將視線角速率穩定在0附近;而PN則容易受到目標機動的干擾,視線角速率出現波動,抗干擾性能差。圖5所示的攔截彈加速度響應曲線也是在彈體結構承受的范圍內,表明所設計的GSM制導律適用于對低空目標的攔截。

2)自動駕駛儀故障對攔截性能的影響(仿真2)。

設自動駕駛儀的故障損失系數f分別取0.2,0.3,0.7,0.8,額外的附加擾動E=25sin0.5t,其他初始參數參照仿真1。

由圖6～圖8可知,導彈自動駕駛儀的故障損失系數越大,說明自動駕駛儀越接近理想正常的工作狀態,所設計的GSM制導律本身有一定的抗干擾能力;可是當故障損失系數f<0.5時,說明自動駕駛儀發生了很嚴重的故障,此時系統已經無法保持穩定,視線角、視線角速率和攔截彈加速度響應均出現很大的超調現象以及發散現象,從而無法將彈目視線角約束至布儒斯特角,同時也無法將視線角速率收斂至0以降低脫靶量,這會嚴重降低末端的攔截性能。

3)CGSM制導律補償后的效果(仿真3)。

設自動駕駛儀的故障損失系數f分別取0.2,0.3,0.7,0.8,額外的附加擾動E=25sin0.5t;式(19)中相關補償系數設置為K=30,α=8,β=6;其他初始參數參照仿真1。

由圖9和圖10可知,式(20)所設計的CGSM制導律可有效補償導彈自動駕駛儀所發生的故障,維持了系統的穩定,確保攔截彈以期望的布儒斯特角跟蹤攔截超低空目標,且由圖11可知,加速度響應曲線最終穩定在0附近,提高了攔截彈系統的抗干擾性能。

5 結束語

基于全局滑模控制原理,設計出一種具有全程魯棒性的GSM制導律,由于省去了滑模趨近模態,可增強系統對環境擾動及參數攝動的抗干擾能力,同時可確保攔截彈在跟蹤低空目標的過程中,將彈目視線角約束在布儒斯特角附近,以降低多徑干擾的影響。針對自動駕駛儀在實際執行制導指令時可能會出現偏差損失,導致視線角速率及視線角發散,影響制導精度的問題,本文設計了CGSM制導律,該制導律大大提高了系統的抗干擾性能,保證攔截彈具有理想的超低空攔截性能,為制導控制一體化的設計提供了理論借鑒。

[1] 王利軍,郭建明,郝晶. 多徑效應對雷達探測低空巡航導彈的影響[J]. 雷達科學與技術,2010,8(1):7-11.

WANG Lijun,GUO Jianming,HAO Jing. Influence of multi-path effect on low altitude cruise missile detection in radar[J]. Radar Science and Technology,2010,8(1):7-11.(in Chinese)

[2] 束川良. 適用于通用布儒斯特角的防空導彈超低空彈道設計[J]. 地面防空武器,2008,39(3):23-26.

SHU Chuanliang. Super low altitude air defense missile trajectory suitable for general Brewster angle[J]. Land-Based Air Defence Weapons,2008,39(3):23-26.(in Chinese)

[3] 王國勝,李蕓. 一種滿足布魯斯特角約束的導引律研究[J]. 現代防御技術,2014,42(3):70-74.

WANG Guosheng,LI Yun. Guidance law for restraint of Brewster angle[J]. Modern Deffence Technology,2014,42(3):70-74.(in Chinese)

[4] 隋棟訓,童創明,彭鵬,等. 超低空目標的廣義布儒斯特效應[J]. 空軍工程大學學報,2015,16(4):29-32.

SUI Dongxun,TONG Chuangming,PENG peng,et al. Study of G-Brewster of super-low altitude target[J]. Journal of Air Force Engineering University,2015,16(4):29-32.(in Chinese)

[5] KORAY S E,OSMAN M. Indirect impact-angle control against stationary targets using biased pure proportional navigation[J]. Journal of Guidance,Control,and Dynamics,2012,35(2):700-704.

[6] LEE C H,KIM T H,TAHK M J. Interception angle control guidance using proportional navigation with error feedback[J]. Journal of Guidance,Control,and Dynamics,2013,36(5):1556-1561.

[7] SHTESSEL Y B,SHKOLNIKOV I A,LEVANT A. Guidance and control of missile interceptor using second-order sliding modes[J]. IEEE Transactions on Aerospace and Electronic Systems,2009,45(1):110-124.

[8] SONG Junhong,SONG Shenmin,ZHOU Huibo. Adaptive nonsingular fast terminal sliding mode guidance law with impact angle constraints[J]. International Journal of Control,Automation and Systems,2016,14(1):99-114.

[9] ZHANG Yunxi,SUN Mingwei,CHEN Zengqiang. Finite-time convergent guidance law with impact angle constraint based on sliding-mode control[J]. Nonlinear Dynamics,2012,70(1):619-625.

[10] KUMAR S R,RAO S,GHOSE D. Nonsingular terminal siding mode guidance with impact angle constraints[J]. Journal of Guidance,Control,and Dynamics,2014,37(4):1114-1130.

[11] LI Guilin,YAN Han,JI Haibo. A guidance law with finite time convergence considering autopilot dynamics and uncertainties[J]. International Journal of Control,Automation,and Systems,2014,12(5):1011-1017.

[12] CHENR H,SPEYER J L,LIANOS D. Optimal intercept missile guidance strategies with autopilot lag[J]. Journal of Guidance,Control,and Dynamics,2010,33(4):1264-1272.

[13] QU Pingping,ZHOU Di. A dimension reduction observer-based guidance law accounting for dynamics of missile autopilot[J]. Journal of Aerospace Engineering,2013,227(7):1114-1121.

[14] 熊思宇,李剛,王華吉,等. 三體對抗中的微分對策協同突防策略[J]. 空軍工程大學學報,2018,19(4):30-36.

XIONG Siyu,LI Gang,WANG Huaji,et al. A cooperative collaborative strategies during three-body engagement based on differential game[J]. Journal of Air Force Engineering University,2018,19(4):30-36.(in Chinese)

[15] BHAT S P,BERNSTEIN D S. Finite-time stability of homogeneous systems[J]. American Control Conference,1997,4:2513-2514.

[16] 辛騰達,范惠林,閆琳. 滑模變結構制導律的抖振問題研究[J]. 航空兵器,2015,2(10):10-13.

XIN Tengda,FAN Huilin,YAN Lin. Study on chattering of sliding mode variable structure guidance law[J]. Aero Weaponry,2015,2(10):10-13.(in Chinese)