Ir是內電壓嗎？IR是外電壓嗎？

黃亦斌郝繼光吳澤宇(江西師范大學物理與通信電子學院，江西 南昌 33007;南昌市灣里區第一中學，江西 南昌 330004)

歐姆定律

描述的是由特定物質——金屬(和電解液)做成的導體的端電壓U和電流I之間的關系。如果導體中有非靜電力，那么就應將其換為含源電路的歐姆定律

此外，還存在閉合電路(或全電路)的歐姆定律

而式(1)可稱為無源電路的歐姆定律。以上兩式中，E為電源電動勢;r為電源內阻。本文討論一些相關的概念問題。

1　Ir是內電壓嗎？——“內電壓”和電壓概念剖析

常見的一種說法是：在式(2)中，U是外電壓，而Ir是內電壓。教材[1]稱：式(3)中的I R(用U外表示)“是外電路上總的電勢降落”(路端電壓)，而Ir(用U內表示)“是內電路的電勢降落”，而文獻[2]、[3]皆明言：Ir“稱為內阻電勢降”。這里說的就是內電壓。

但Ir是內電壓嗎？如果是，那么它是哪兩點之間的電壓？是正負極之間的電壓嗎？正負極之間的電壓是路端電壓。Ir是正負極之間經過內電路的電壓嗎？靜電力做功與路徑無關，經過內電路的電壓和經過外電路的電壓一定相同，故而還是路端電壓。可見，“Ir是哪兩點之間的電壓”這個問題找不到答案。

與此相關的問題是：如果Ir是內電壓，那么其對應的電場分布在哪里？在電源內部？但剛才已經說明，正負極之間經過內電路的電場強度的積分大小不是Ir而是U外=IR。所以，這個問題也找不到答案。

上述兩個問題，很可能是偽問題，因為“內電壓”所指稱的電壓可能因沒有相應的電場而根本就不存在!

仔細思考后會發現，在電源內部，凡是有非靜電力的地方，其對應靜電場的場強積分(即電壓)只能是式(2)中的U，而不會等于其中的Ir;而在沒有非靜電力的地方，根據式(1)，Ir才會等于電壓U。(這里的U和Ir都只針對該段導體而言，非整個電源的U和Ir。)

我們通常談論電源時，常常默認其內部處處有非靜電力。有時確實如此(如切割磁感線的導體)，有時并非如此(如化學電池)。無論是何種情況，通通處理為“處處有非靜電力”并不會影響電流、路端電壓、功率等我們感興趣的物理量，但會影響“內電壓”的存在性。

如圖1(a)所示，對于處處有非靜電力(圖中未畫出)的情形，從其電勢變化圖中可以看出，根本沒有哪段對應Ir。對于圖1(b)中的化學電池，在正、負極與電解液之間極薄的反應層(即BC段和DA段)內，存在很大的非靜電場和與之抗衡的靜電場，導致電勢躍變，而且其內阻可以忽略;而在CD段的電解液中，沒有非靜電力，只有靜電力。此時，BC段和DA段的電勢躍變之和等于電動勢，而CD間的電勢降落才等于Ir。文獻[1]中的圖2.7-2與此類似。

兩點說明：(1)化學電池中的內電壓，僅指CD段。千萬別認為“內電壓”真的是指電源內部的電壓，因為后者明顯包含3段電壓：BC段，CD段和DA段，且其代數和就等于路端電壓。(2)如果這3段電路分別有內阻r1，r2，r3，那么Ir=I(r1+r2+r3)仍然不對應任何電壓，僅Ir2才等于CD段電壓(這其實就是無源電路的歐姆定律)。

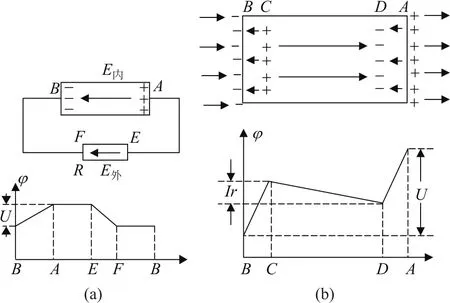
圖1　電路圖和電勢隨回路的變化圖

總之，我們常說的“內電壓”(或“內電路的電勢降落”“內阻電勢降”)這一概念其實是需要小心使用的。在有非靜電力的地方(尤其在電磁感應中的動生或感生電動勢場合)，確實存在電壓，但不是等于Ir的那種“內電壓”;后一種“電壓”和相應的電場其實不存在。電源內部僅在非靜電力不存在的地方，才存在等于Ir的內電壓(這里r僅為該段的電阻)。但這跟電源外部存在等于IR的電壓沒什么本質不同。教材[1]講解的恰是化學電池，且假定了r1=r3=0，故Ir確實等于內電壓(CD段)。

還可以看出，“外電壓”一詞是具有誤導性的，它讓人以為，從正極到負極，經過外電路還是經過內電路，其電壓不同。實際上，由于靜電場的保守性∮E·d l=0，從正極到負極的任意路徑的電壓都相等，不論是經過內電路還是外電路，也不論是經過導體內部還是外部。圖2(a)中的4條路徑的電壓全部相等。(注意導線表面以及不同金屬交界面上都會有或正或負的凈電荷分布，而所有電荷的共同作用將使得上述論斷成立。圖中只畫出了電源兩極的電荷。)故最好的做法是只使用“路端電壓”的稱呼。

“內電壓”一詞則具有更大的誤導性。首先，等于Ir的“內電壓”不一定存在。即使存在，它也不是電源內部兩極間的電壓。而在化學電池中，CD間(見圖2(b))經過路徑1(內電路)的電壓和經過路徑2(兩個反應層和外電路)的電壓相等，都是所謂的“內電壓”。這里的“內”字頂多表明C、D兩點在電源內部而已，對路徑沒有任何限制。另外，我們引入“內電壓”其實只是想指稱Ir而已，而從下面的分析可以看出Ir有另外的意義和表達。故而應該摒棄“內電壓”“內阻電勢降”等詞匯。

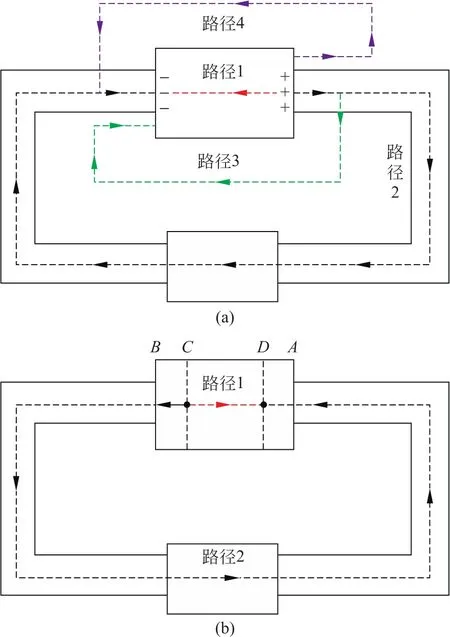
圖2　電壓的路徑無關性

2　IR是外電壓嗎？——IR(和Ir)的物理意義

注意筆者說的是“Ir等于內電壓”，而不是“Ir是內電壓”。前者是指數值相等，而后者是術語定義。我們只能說：

(1)場強的線積分(或位移在場強方向分量與場強的乘積)是電壓;

(2)Ir等于內電壓，IR等于外電壓。

第一句是定義，而第二句指數值關系。把第一句中的“是”換為“等于”，我們仍能將其正確地理解為是定義，但將第二句中的“等于”換成“是”，則極易被認為是定義而造成概念混亂。

為了說明電壓U和IR(或Ir)確實是兩碼事，我們看一些例子。①對于有非靜電力的一段金屬，根據式(2)，U≠Ir，即Ir不等于電壓。②對于無非靜電力的非線性元件，歐姆定律式(1)不成立：U的意義明確，而R和IR無甚意義，“I R是否是電壓”更無從談起。

那么，對于無非靜電力的金屬導體(這是線性元件)，式(1)一定成立嗎？或者，金屬導體的I R在原則上到底表示什么物理意義？我們需要從微觀上重新審視歐姆定律。

許多教材[2-5]都從微觀上用經典理論解釋了歐姆定律的來源。當加上電場E后，電子在熱運動速度的基礎上疊加定向運動速度。但電子與晶格(即金屬骨架，或晶體點陣的原子實)碰撞后該定向運動速度消失，電子被重新加速，作勻加速運動。于是，平均定向速度v與場強成正比：|v|∝|E|。然后利用電流密度的表達式

(q=-e為電子電量;n為單位體積內的自由電子數)便得到歐姆定律的微分形式

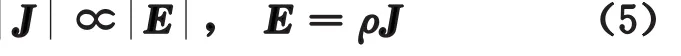
其中ρ就是電阻率。對于一段均勻導體，利用U=El，I=JS，R=ρl/S，上式即變為常見的歐姆定律式(1)。

從平均意義上來講，電子受靜電力Fe=q E作用在晶格中作勻速運動，形成穩恒電流。但怎么能平衡呢？注意微觀解釋中還有一個因素——與晶格的碰撞，故而平均來說，是晶格施予的阻力f與靜電力平衡(如圖3(a)所示)：

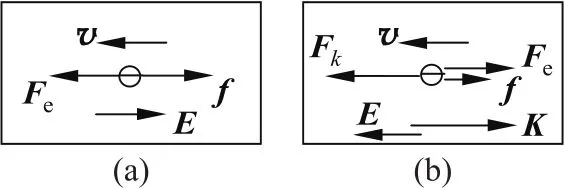
圖3　平均而言電子受力平衡

考慮到靜電力Fe的宏觀體現是式(1)中的U，故而式(6)與式(1)必須相當，也就是說，IR的物理本質就是晶格施予電子的(平均)阻力!具體地，f=-Fe=-q E，考慮到式(5)和式(4)，有

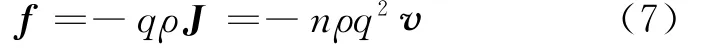
這可以視為晶格阻力的決定式，它與自由電子的(平均定向)速度成正比。而在導體(或晶格)也有運動的情形，式(7)顯然需要修改為

其中v′是電子相對于晶格的速度。這就是說，晶格阻力永遠阻礙電子與晶格的相對運動。式(7)和式(8)可以成為討論普通金屬電流的一個原始出發點。

既然U是靜電力的體現，其意義是靜電力對單位電荷所做的功，那么IR作為晶格阻力的體現，其意義就是晶格(平均)阻力對(作平均定向運動的)單位電荷所做的功。

在含源電路情形，電子受靜電力Fe=q E、晶格阻力f和非靜電力Fk=q K(K為非靜電場強)這3個力而平衡(如圖3(b)和下文表1所示)：

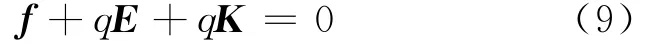
將式(7)代入，即得

這就是含源電路歐姆定律的微分形式。它表明，靜電場強和非靜電場強的矢量和決定了電流的大小和方向。考慮電源內部從負極到正極的位移l，注意E=K·l，U=-E·l，ρJ·l=Ir，由式(10)即可導出積分形式式(2)(其中的U和I為代數量，正方向的規定見圖4)。

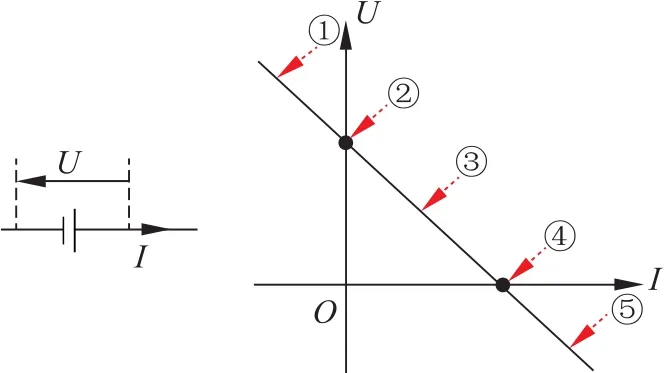
圖4　線性電源的伏安特性曲線及5種可能狀態

一般而言，電源有5種可能的狀態：①充電;②斷路;③普通放電;④短路;⑤異常放電(電流正向，且大于短路電流)。它們在電源的伏安特性曲線上的對應如圖4所示。電子受力平衡關系式(9)、含源電路歐姆定律的微分形式式(10)及其普通積分形式式(2)這3個關系，在電源的不同狀態下有不同的表現。表1例舉了3種情形，其中所有的標量都是非負的算術量。從中可以反復看出，Ir源自晶格阻力，與靜電力和電壓無關。

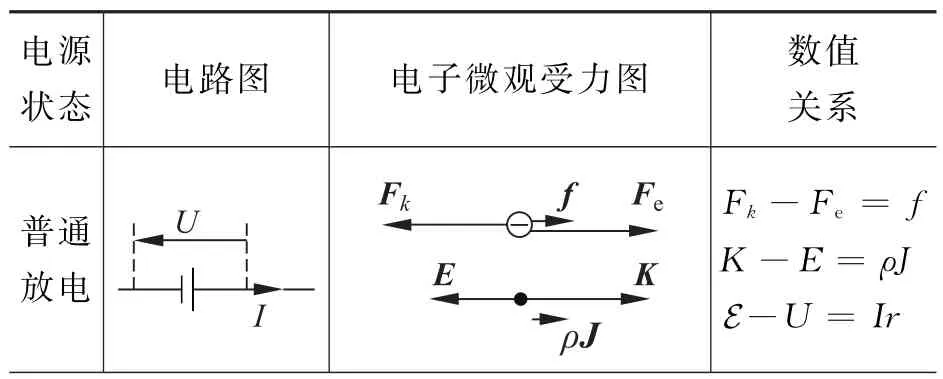
表1　電源狀態與對應的微觀圖像舉例

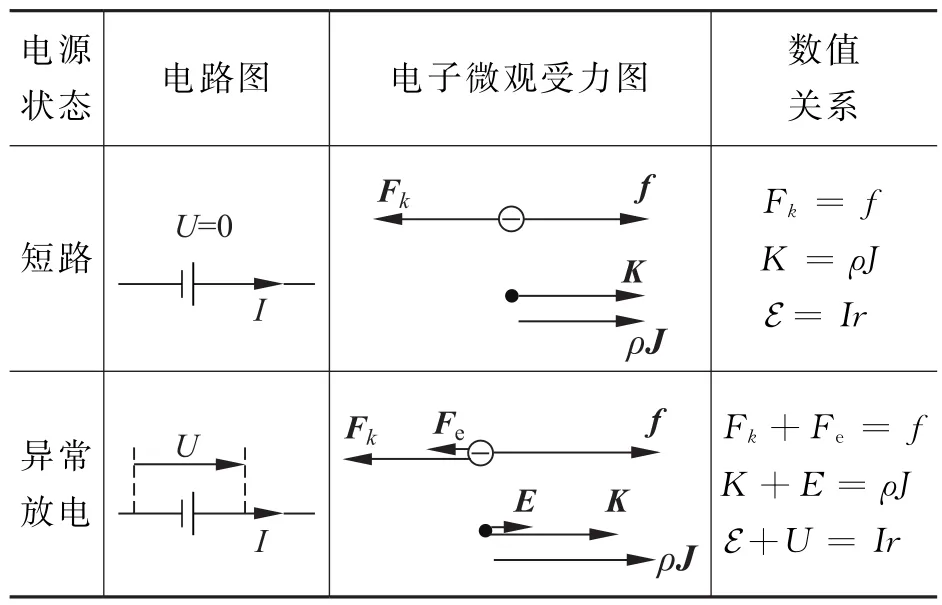
續表

3　無電壓、但有Ir的情形

由于晶格阻力與靜電力、非靜電力無邏輯關聯，故而它并不必然跟后者平衡，從而式(1)～(3)并不必然成立。由此引出兩個問題：首先，為什么通常只見到它們成立的情況？那是因為電子質量太小，通常作無慣性處理。此時電子受力必須平衡，即使有加速度(平均而言)也是如此。不論是各種暫態電流還是交流電，我們都使用式(1)～(3)，即默認電流跟電壓與電動勢之和永遠同步變化。這其實就是說，微觀上式(9)總成立。

其次，式(1)～(3)何時不成立？自然是必須考慮電子慣性的特殊情形。此時，式(9)需修改為

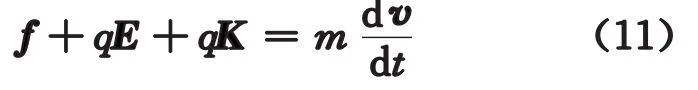
將速度v用J表示(見式(4))，把式(7)代入，可知對應的歐姆定律的微分形式(10)和積分形式的式(2)就要分別修改為

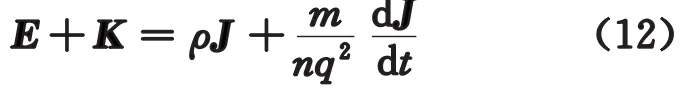
和

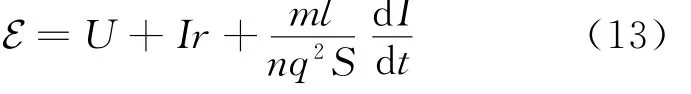
1916年，Tolman和Stewart使一塊金屬快速往復運動，并測到了交變電流。這顯然是由于電子有慣性而跟不上晶格的運動所致，與電動勢和電壓無關。由此測出的荷質比與陰極射線中電子的荷質比相當，證明金屬中的載流子就是自由電子。文獻[5]指出，歐姆定律要求場強的變化周期遠大于電子平均定向運動時間。如果頻率高過微波段，電流與場強將不再同相位。這就是說，電子慣性開始起作用了。這些例子中出現的電流與通常的穩恒電流、暫態電流和交流電截然不同，可將后者稱為“同步電流”(滿足式(9)、(10)和式(2))，而將前者稱為“非同步電流”(滿足式(11)～(13))。

由于IR只是晶格阻力的表現，焦耳熱功率也就應該只是阻力生熱的功率。具體地，一段導體內有n Sl個自由電子，每個電子所受阻力的功率為f·v，故總功率為

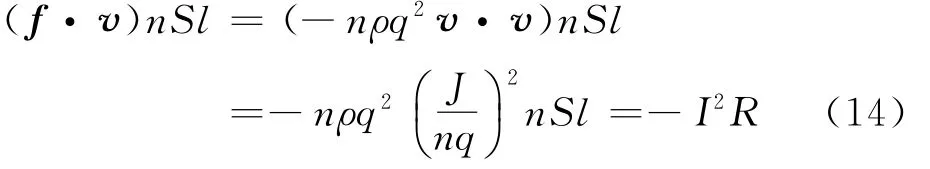
這就是焦耳熱功率。或者，由于IR是阻力對單位電荷所做的功，將其乘以電量d q=I d t，即得阻力做功為I2R d t，也得到焦耳熱。

例如，考慮一個金屬環繞垂直于環面的對稱軸勻速轉動，然后被突然卡住(即晶格突然靜止)。此時環中會出現由于電子慣性導致的“非同步電流”，可用式(13)(令E=U=0)處理。經過一段時間后電流消失，電子(定向運動)動能轉化為焦耳熱。這里沒有任何靜電力、電壓和電功率，卻出現了焦耳熱。若考慮自感，可把E=-L d I/d t代入式(13)，其能量轉化環節中多了磁場能，但仍未出現靜電場、電場能和電功率。

4　小結與命名

文獻[3]指出：“從金屬經典理論來看，電阻反映的是自由電子與晶體點陣上的原子實碰撞造成對電子定向運動的破壞作用，這也是電阻元件產生焦耳熱的原因。”本文觀點與此相符。電流和電阻相伴而生：因為有“流”(定向運動)，所以受“阻”;阻力正比于速度，從而正比于電流。這才是電流和電阻的物理本質，從而跟電場、電壓無必然聯系。

可見，將Ir稱為內電壓(如果確實存在這么一段電壓的話)、將I R稱為外電壓，這些做法是不合適的。非靜電力和阻力都不是靜電力，從而E和IR都不是電壓，就像不能把熱量、功和能量當成一回事一樣。當然，這種做法也可以理解，因為它們具有相同的單位，可以相加減，而且IR本身的物理意義很少被明確，連一個稱謂都沒有，更別提字母代號了。之所以將I R和Ir稱為電壓，一個可能的原因就是無以名之，只好用“電壓”將就，久而久之還真把它們當電壓了。

根據以上分析，IR具有獨立、明確的物理意義，該享有配備稱謂的待遇。思來想去，也許稱IR為“流阻”比較合適，記為H。如果這樣，則物理量“流阻”H的意義是晶格(平均)阻力對(作平均定向運動的)單位電荷所做的功，與電流成正比，定義式是H=IR(正如電壓的定義U=El)，單位是V。3個歐姆定律(1)～(3)式可分別寫為U=H、E=U+H內和E總=H外+H內，它們都只對“同步電流”成立。“流阻”可以單獨存在，獨立于電動勢和電壓。如果不引入“流阻”一詞，不介紹IR的物理意義，那么只能說“通常I R等于電壓(或電動勢與電壓之差)”，其中“通常”是指普通的“同步電流”，“等于”是指僅數值相等。

當然，“流阻”H這個概念存在的前提是線性條件，該條件可以用阻力決定式式(7)來表征。實際上，各種歐姆定律的成立和電動勢、內阻等概念的存在原則上皆以線性條件為前提。(式(12)、(13)仍可冠名為“歐姆定律”，因為其使用了反映線性特征的式(7)，出現了ρJ和Ir項。)具體地，當某元件(電阻或電源)的伏安特性曲線是直線時，我們用其斜率定義其電阻(內阻)，用其與U軸的交點定義電動勢。而在非線性情況下，我們只能得到一條較為一般的伏安特性曲線而已。如果該曲線仍有一些較好的性質，那么也許可以據此定義出一些物理量來，但這些物理量的意義高度依賴于該曲線的具體性質。而電流、電壓則與線性條件無關，比如在畫一條一般的伏安曲線(非線性)時就使用了電流、電壓的概念。

5　幾點附注

首先，式(2)和式(3)的區別不僅僅是做了一次代換那么簡單。式(1)和式(2)都針對部分導體，屬局部特征，都存在微分形式(見式(5)和式(10));但式(3)針對全電路，屬整體特征，無微分形式，其中的E=∮K·d l是全電路的總電動勢，而電壓由于∮E·d l=0而消失。

其次，保守與否決定了談論“內”“外”是否不妥。前面談到，“外電壓”有誤導性，“內電壓”問題更大，其基本原因就是靜電力是保守力，這導致電壓無需“內”“外”這種詞匯來加以限定。但對于式(10)中非保守的非靜電力和阻力，由于∮K·d l=E≠0，∮ρJ·d l=∑iIiRi≠0，從而兩點間的積分對不同的路徑(經過內電路還是外電路)會不同，故而談論“內外”是有意義的，如內阻、外阻、“外電動勢”(如電動機的反電動勢)等。

另外，有人認為式(3)只適用于純電阻電路，這其實要看其中的E指什么。以電路中含電動機為例。對全電路而言有

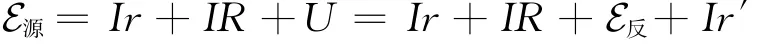
其中，r′為電動機的內阻;E反為電動機的反電動勢，它把電能轉化為動能。若僅把E源當成式(3)中的E，那么式(3)確實只適用于純電阻電路;但若把所有的電動勢和反電動勢都算成E(畢竟它們都是非靜電力)，則有

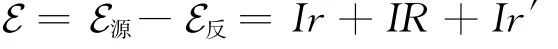
此時式(3)就當然適用于所有電路。實際上，電路中除了靜電力就是非靜電力和阻力，而∮E·d l=0保證總電壓(或靜電力項)一定消失，從而只剩下非靜電力項(表現為總電動勢)和阻力項(表現為總“流阻”)。故而，只要對E作出適當的解釋，式(3)就適用于一般電路(當然以“同步電流”和線性條件為前提)。