民用飛機反尾旋研究與尾旋風洞試驗

顏　巍　黃靈恩　陳　功 /

(上海飛機設計研究院，上海201210)

0　前言

尾旋是飛機的極限飛行狀態之一，若飛機不幸陷入此一狀態，飛行員要毫不猶豫地通過正確的舵面組合操縱來迫使飛機迅速地從尾旋中改出。傳統的尾旋改出方式有[1]：“三中立”法、“反舵推桿”法、“平中順”法、“舵回中推桿”法和“反舵桿回中”法等。其中“三中立”法操作最為簡便，飛行員無需判別尾旋的方向；“反舵推桿”法操作改出效果最佳，但需要準確判斷尾旋的方向，改出后桿舵要及時回中；“平中順”法操作適用于方向舵近乎完全失效的狀態。在飛機A的研究過程中，從人機的終極安全角度考慮，需要研究飛機是否具有尾旋改出的能力，以備在極端危險情況下，飛行員具備最佳的處置方式。由于靜態測力結果為飛機總的空氣動力的主量，所以首先在常規風洞中進行了飛機縮比模型的大攻角靜態測力試驗。飛機尾旋運動以偏航運動最為顯著，所以首先對方向舵、副翼的單獨偏轉的影響進行分析；此外為了降低攻角，要對升降舵的單獨偏轉的影響進行分析。在大攻角條件下，飛機舵面效率會大幅下降，有時甚至完全喪失。在舵面操縱無效的情況下，反尾旋傘就是人機存活唯一的、最后的選擇，所以設計一款合適的反尾旋傘是極端重要的，它關系到飛行員的生命安全和價值上億元飛機的保全。

1　舵面組合偏轉法改出尾旋

1.1 方向舵的影響

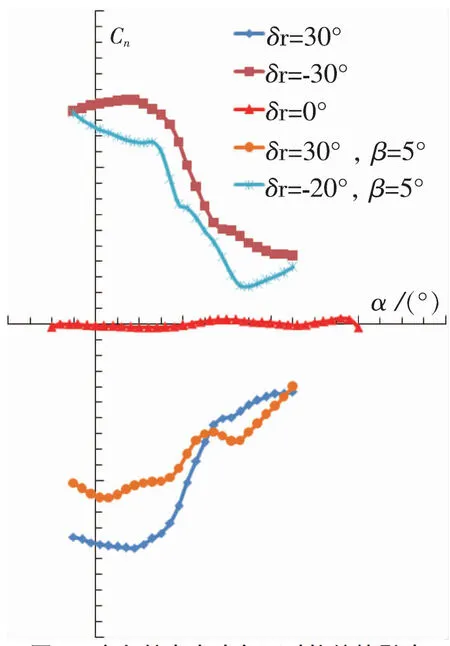
圖1　方向舵在大攻角下對偏航的影響

為了將處于尾旋狀態的飛機改出，首先要制止飛機的旋轉，即降低偏航角速率，為此需要將方向舵回中或逆尾旋方向偏轉方向舵，消除那些有利于、可能助長或保持飛機旋轉的順尾旋偏航力矩。圖1中展示了取自飛機模型大攻角試驗結果，β=0°時的不同方向舵偏度下的Cn隨攻角變化關系。當r=-30°時，近似對應飛機右尾旋，Cn為正值。若方向舵回中，即r=0°，Cn值降到零附近，即消除了順尾旋的偏航力矩，飛機將會逐漸停止旋轉。若方向舵向反方向滿偏，即r=30°，則Cn值全部反號，產生了逆尾旋偏航力矩，迫使飛機停止旋轉的時間將更短。從小攻角到大攻角，方向舵效率下降了約70%。圖1還展示了β≠0°時的不同方向舵偏度下的Cn隨攻角變化關系。當r=30°時，近似對應飛機左尾旋，外側滑，Cn為負值。若方向舵向反方向偏轉，即r=-20°，則Cn值全部反號。大攻角條件下，方向舵效率僅有約30%。這個結論說明，該飛機在尾旋中即使帶有外側滑，只要逆尾旋方向偏轉方向舵就能制止旋轉，當然，從實施改出工作到停止旋轉的時間長短與飛機尾旋改出前的初始條件有關，如攻角的大小，隨著攻角的增大，方向舵的效率會下降，改出時間會延長。可以看出飛機尾旋中若逆尾旋方向偏轉方向舵是能夠提供抗尾旋的偏航力矩的。

1.2 副翼的影響

飛機除了方向舵能夠提供主要的偏航力矩外，副翼偏轉在提供滾轉的同時也能提供一小部分偏航力矩。操縱副翼的原因是，隨著攻角的增大，方向舵受平尾/機身/機翼洗流的影響逐漸加大，當超過某一攻角，方向舵效率會全部喪失，此時唯一能提供偏航力矩的就是偏轉副翼，因為副翼處于機翼的外翼，不受其它部件洗流的影響，且氣動中心到重心處的力臂較長。圖2中展示了β=0°時的不同副翼偏度下的Cn隨攻角變化關系。由于在大攻角條件下副翼所提供的偏航力矩出現反號現象，所以若在飛機左尾旋中，向右壓操縱桿反而加劇偏航的程度，而向左壓操縱桿可以產生逆尾旋的偏航力矩，有助于尾旋改出。圖2中展示了β≠0°時的不同副翼偏度下的Cn隨攻角變化關系。在有側滑的大攻角條件下，左、右壓桿對Cn的影響的趨勢基本相同，但量級不同。飛機左尾旋中，向右壓操縱桿會加劇偏航的程度，若向左壓操縱桿會減小順尾旋偏航力矩的量級。可以看出飛機尾旋中若順尾旋方向偏轉副翼能夠提供小量級的抗尾旋偏航力矩。

1.3 升降舵的影響

由于沒有進行飛機模型的旋轉天平試驗，只能用飛機模型大攻角靜態測力試驗結果來近似地評估飛機在尾旋改出中升降舵的作用。圖3展示了取自大攻角試驗結果，飛機模型基本構型條件下，不同升降舵偏度所對應的俯仰力矩系數曲線關于x軸的鏡像曲線(Cm_氣)與基于理論計算的不同旋轉角速度條件下的慣性上仰力矩曲線(Cm_慣)之間的關系，其中Cm_慣=f(α，ω，Ix，Iy，q，S，c)。圖中紅色虛線對應了δe=-30°，即順尾旋方向偏轉升降舵，這條線與不同旋轉角速度條件下的慣性上仰力矩曲線均有交點，即氣動下俯力矩與慣性上仰力矩的平衡點，說明δe=-30°條件下是會出現平衡尾旋的，但從圖中不能判定每一個交點的穩定性。圖中黑色虛線對應了δe=0°，即升降舵回中，綠色虛線對應了δe=15°，即逆尾旋方向偏轉升降舵。根據公開的資料，尾旋試驗飛機模型的旋轉角速度沒有超過330°/s的情況，大攻角條件下，黑色虛線(升降舵中立)和綠色虛線(逆尾旋偏轉升降舵)均在ω=330°/s所對應的曲線上方(土黃色實線)，所對應的含義是δe=0°/15°所產生的氣動下俯力矩大于慣性上仰力矩，即升降舵中立與逆尾旋偏轉升降舵均有能力將飛機從尾旋狀態改出。當然在實際操作中，首先需要逆尾旋方向偏轉方向舵制止飛機的旋轉。

1.4 平尾-升降舵和垂尾-方向舵的綜合影響

對于飛機尾旋改出能力的評估，除了包括對平尾-升降舵和方向舵各自獨立的評估，還要將兩者綜合起來考慮和分析。 Ralph W Stone和Sanger Burk[2]等人為了研究飛機的尾段布局對飛機尾旋改出特性的影響，利用一個1/10的飛機模型在NASA蘭利研究中心Φ=20 ft的立式風洞進行了旋轉天平試驗，通過試驗來研究平尾-升降舵和垂尾方向舵對尾旋改出的影響。試驗結果顯示若固定某一尾旋攻角，且當垂尾位置相對重心位置固定時，增加平尾氣動中心到飛機重心的距離，將導致飛機的尾旋攻角減小，反之，則使得飛機的尾旋攻角增大。若固定平尾-升降舵和方向舵的位置，即固定各自氣動中心到飛機重心的距離，隨著尾旋攻角的增大，即由陡尾旋向平尾旋方向發展，垂尾-方向舵受平尾-升降舵洗流區的影響逐漸增大，使得垂尾-方向舵的偏航力矩隨之減小，表明使用方向舵偏轉迫使飛機停止旋轉的能力在下降。美國NASA蘭利研究中心立式風洞的研究人員(Neihouse、Lichtenstein、Pepoon，1946年)和英國RAE的研究人員(E. Finn，1946)[3]在進行了長期而大量的試驗后，總結出了一套經典的判定飛機改出尾旋能力的方法：TDPF～[(Ix-Iy)/(mb2)]判據法。其中TDPF為“Tail Damping Power Factor”，這個指示參數由TDR(Tail Damping Ratio)和URVC(Unshielded Rudder Volume Coefficient)兩部分組成，前者影響穩定平衡尾旋的攻角(陡尾旋還是平尾旋，在早期研究中沒有緩尾旋的定義)，后者指示未受平尾-升降舵洗流影響的方向舵有效面積和力臂長度。它們的數學表達式如下：

TDPF=URVC × TDR

(1)

其中：TDR=(SFL2)/[S(b/2)2]，URVC=(SRL1)/(Sb/2)

SF為平尾下方的機身外表面在機身對稱面的投影面積；SR為未受平尾和升降舵洗流影響的，仍然能夠保持舵面效率的那部分方向舵的面積在機身對稱面的投影面積；L為飛機重心到SF幾何中心的距離；L1為飛機重心到SR幾何中心的距離，如圖4所示。

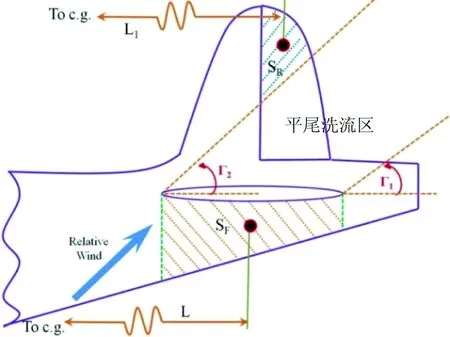
圖4　TDPF～[(Ix-Iy)/(mb2)]判據法所定義的相關幾何參數

首先求出TDR，若TDR>0.019，平尾當地攻角可以假定為αtail=30°，則Г1=15°，Г2=45°。根據這個定義，從飛機的3D數模上可以近似的求出SR的面積，進而可以求出URVC，最后求得TDPF。

為了完成尾旋改出能力的判定，還需要計算飛機的偏航力矩慣量參數(Inertia Yawing-Moment Parameter)：[(Ix-Iy)/(mb2)]。此外由于飛機的尾旋特性與改出特性和飛機所處的飛行高度(大氣密度)有關，所以還需要計算飛機的相對密度系數：μ=m/(ρSb)。在完成以上工作后，就可以將點{TDPF，[(Ix-Iy)/(mb2)]}標注在TDPF～[(Ix-Iy)/(mb2)]判據圖中，如圖5所示。

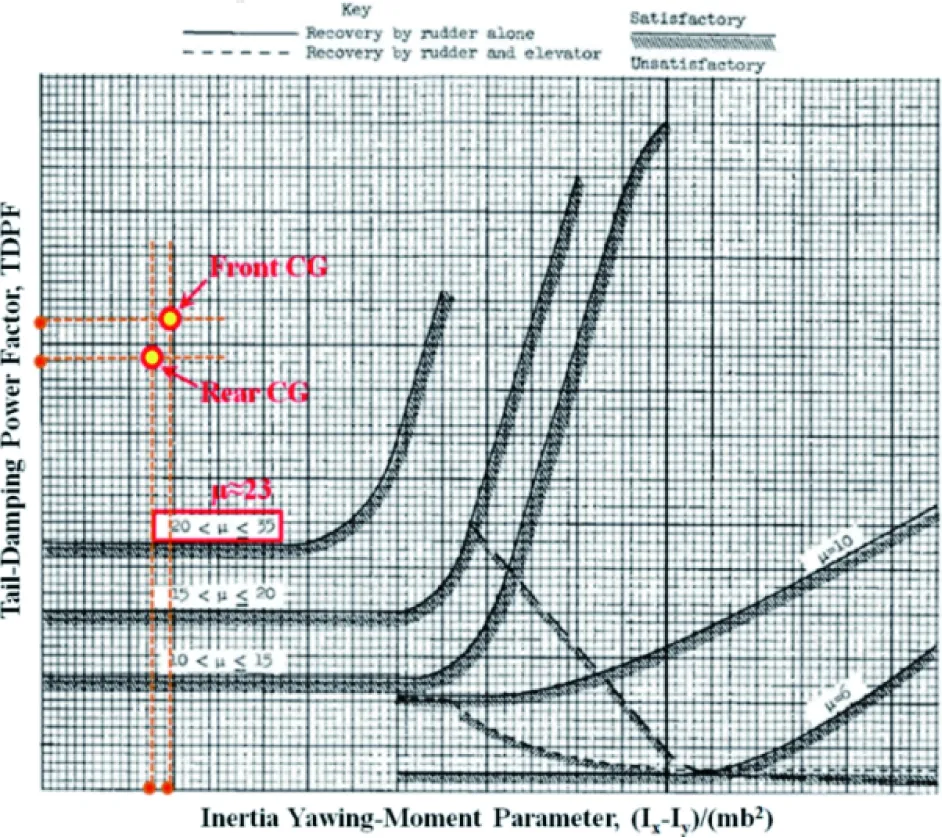
圖5　TDPF～[(Ix-Iy)/(mb2)]判據圖

從圖5中可以看出無論前重心所對應的點，還是后重心所對應的點，均處于μ∈(20，35)所對應曲線的上方，且余量很大，這表明在僅使用方向舵條件下，就能夠使飛機改出尾旋。

1.5 試驗驗證

以上分析均是基于靜態測力試驗結果和經驗公式，為了檢驗以上的結論，需要通過尾旋風洞試驗進行相關的驗證。為此制作了一個滿足外形和動力學相似準則的無動力飛機模型，在尾旋風洞中進行飛機模型的尾旋改出試驗。圖6展示了在相同模態的尾旋狀態下，實施不同改出方法的改出效果比較，比較參數為攻角與偏航角速率。從圖中可以清楚的看到采用反舵推桿方法的改出效果最佳，其余兩種包含方向舵均回中的改出方法的效果均不及反舵推桿法。這也驗證了前文中TDPF～[(Ix-Iy)/(mb2)]判據的準確性，即對于這架常規布局的運輸機的尾旋改出，方向舵起到主要的作用。

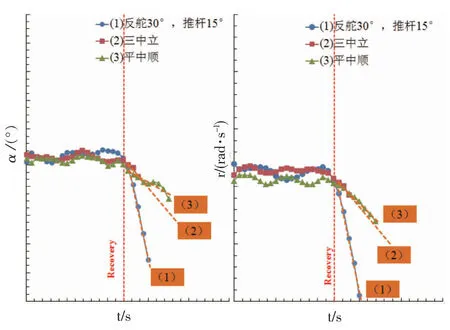
圖6　不同改出方法的改出效果比較

2　反尾旋傘改出尾旋

2.1 反尾旋傘的研制

當飛機進入尾旋飛行狀態時，試飛員通過舵面操縱無法改出時，則需借助反尾旋傘提供一個附加的低頭力矩與偏航力矩，以抵消飛機的慣性上仰力矩與偏航力矩，強行迫使飛機從尾旋中改出，直到恢復正常飛行狀態。為了保證反尾旋傘能提供足夠的低頭力矩和偏航力矩，需要對反尾旋傘的阻力特征值CDSD、連接繩長度Lr、傘載荷進行估算。由于立式風洞試驗模型的比例較小，模型內部結構和強度與真實飛機相差較大，同時立式風洞試驗主要關注打傘后，傘的阻力對飛機飛行姿態的影響，所以這里不進行傘載荷的估算。為獲得合適的反尾旋傘的阻力面積CDSD和連接繩長度Lr，本文使用了工程估算法與原準機類比法兩種方法來探討反尾旋傘的特征尺寸。

2.1.1 工程估算法[4]

確定傘的阻力面積和傘繩長度時，應有一個參考基準，為此可以通過以往的工程經驗和已有的經驗公式來確定這些參數，以下通過幾種不同的工程估算方法進行估算。

1 ) AVP-970提供的工程估算方法

根據AMX飛機尾旋傘研制報告DesignandAirworthinessRequirementsforServiceAircraft，IRVIN阻力傘公司在咨詢了英國相關科研機構后，對一架未知尾旋特性的飛機給出的反尾旋傘阻力面積與傘繩長度估算式為：

CDSD=0.091 4×SLs/LA

(2)

Lr≈1.1～1.3L

(3)

式中，CD為反尾旋傘阻力系數，一般取值0.5～0.55；SD為反尾旋傘特征面積(m2)；S為機翼參考面積(m2)；Ls為飛機翼展(m)；LA為傘鉤到飛機重心的距離(m)；L為機身長度(m)；Lr為傘繩長度(m)。

2)美國軍用標準MIL-STD-1797A提供的工程估算方法

參考MIL-STD-1797A，為了改出嚴重失速尾旋狀態，需要克服慣性上仰力，假定升降舵、方向舵徹底失效，完全依靠反尾旋傘時，反尾旋傘必須提供如下的下俯力矩：

(4)

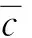
式(4)右邊中的第一項為反尾旋傘打開后所克服的抬頭靜力矩，第二項為反尾旋傘打開后克服飛機的慣性力矩。可以看出飛機俯仰慣性矩越大、飛行時動壓越小，那么所需反尾旋傘的阻力面積CDSD越大。MIL-STD-1797A所提供的Lr經驗算式如下所示：

Lr=1.1×L

(5)

以上二種估算方法給出的傘的基本參數有一定差異，如表1所示，這是由于這些公式產生于不同的時期以及不同的國家，適用于不同的飛機。這樣僅用工程估算法來設計反尾旋傘就帶來較大的不確定性，需要引出其它的方法來進行相關的對比才能確定。

表1　經驗公式估算的反尾旋傘基本參數

注：A≈B，F≈G 。

2.1.2 原準機類比法[4]

原準機類比法是指通過對已有的民用客機的反尾旋傘數據的統計，按照重量、慣性矩、飛機氣動外形等特點進行類比，估算所研制的反尾旋傘的尺寸，圖7為典型民用飛機反尾旋傘阻力面積與重量之間的關系。由統計結果可知，飛機A的全機重量與MD-90飛機的全機重量近似，所以可以選用MD-90飛機所使用的反尾旋傘，通過表中可以得到所對應的阻力面積H。通過和上面不同工程估算法所獲得的阻力面積的對比，發現原準機類比法獲得的阻力面積H與工程估算法中AVP-970和美國MIL-STD-1797A兩種方法所估算的阻力面積值較為接近。

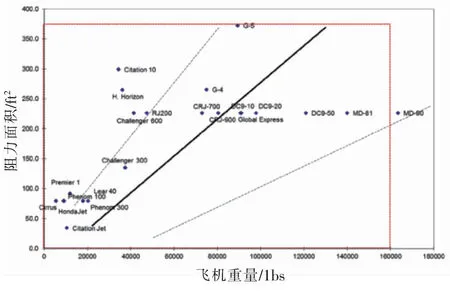
圖7　飛機反尾旋傘阻力面積與飛機重量關系

通過圖8可以估算出反尾旋傘傘繩長度約W m，與AVP-970和美國MIL-STD-1797A兩種工程估算法獲得的傘繩長度比較接近。

圖8　飛機反尾旋傘傘繩長度與機身長度關系曲線

以上通過AVP-970和美國MIL-STD-1797A兩種工程估算方法，以及原準機類比法所求得的反尾旋傘特征參數比較接近，所以傘阻力特征值暫定為CDSD≈A m2，傘繩長度暫定為Lr≈Fm。為了有所比較另外設計了兩個不同面積的傘，一個面積比A大，一個比A小；還設計了兩個傘繩長度，一個比F大，一個比F小。

IRVIN公司的經驗指出：為了避免估算反尾旋傘特性出現重大失誤，必須謹慎使用上述公式，必須通過立式風洞試驗或模型自由飛試驗進行必要的驗證，才能較好的確定傘的尺寸。

2.2 試驗驗證

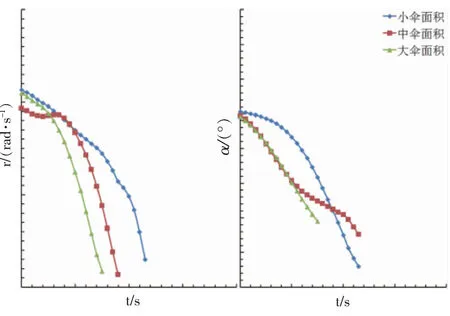
圖9　傘面積大小對飛機尾旋改出影響比較

圖10　傘繩長度對飛機尾旋改出影響比較

在尾旋風洞中進行的反尾旋傘選型試驗結果如圖9和圖10所示。圖9為不同傘面積大小對尾旋改出的影響，當使用大號傘攻角和偏航角速率降到零所需時間最短。可以看出隨著傘面積的增大，改出效果越好，基本為單調關系。圖10為不同傘繩長度對尾旋改出的影響，可以看出當使用中傘繩長度時，攻角和偏航角速率降到零所需時間最短，而使用長傘繩和短傘繩的改出時間較長，改出效果均不如前者。綜合評價，選擇最大傘面積的傘和中等長度的傘繩，尾旋改出的效果最佳。需要補充說明此一選擇假定了飛機尾部強度滿足開傘沖擊載荷。

3　結論

通過系統的分析和研究，使用了一套適用于工程應用的預測飛機采用舵面組合法改出尾旋的方法，利用飛機模型的大攻角靜態測力試驗數據中各有關舵面偏轉的氣動力結果評判單獨偏轉舵面對尾旋改出能力的影響。利用美國NASA所使用的評判飛機尾旋改出的經驗公式得出常規布局運輸機改出尾旋主要依靠方向舵的偏轉。最后在尾旋風洞中通過動態風洞試驗進行了相關的驗證，得出飛機A改出尾旋的最佳方法為反舵推桿法。此外，總結并利用國際上通行的反尾旋傘設計方法設計了不同規格的反尾旋傘，通過尾旋風洞試驗對反尾旋傘進行了選型，通過試驗結果分析，選擇了最佳的傘面積和傘繩長度。在滿足飛機結構強度的前提下，采用最大號面積的傘與中長度傘繩組合改出飛機尾旋的效果最佳。