基于LSTM神經網絡的公交移動支付預測模型
梁肖裕 苗晨 山東科技大學信息管理與信息系統
關鍵字:LSTM 邏輯回歸分類器 混淆矩陣檢驗
1 應用背景
我們擁有的初始數據集是某城市安裝四分之一的移動支付設備時,全部公交的移動支付情況。那么,該城市的公交車全部安裝移動支付設備后,當前移動支付人數的四倍約為全部安裝移動支付設備后的總乘車人數。利用這個關鍵信息,使用LSTM神經網絡對人數進行預測。
2 LSTM神經網絡
LSTM網絡的訓練采用誤差的反向傳播算法,當前細胞的狀態會受到前一個細胞狀態的影響。同時在誤差反向傳播計算時,當前單元的輸出誤差不僅僅包含當前時刻T的誤差,也包括T時刻之后所有時刻的誤差,這樣每個時刻的誤差都可以經由當前單元的輸出和前一時刻單元的輸出迭代計算。
經過訓練后,我們利用LSTM的記憶特點,對全部安裝設備后的公交卡支付人數進行預測,再與移動支付人數進行對比。通過數據對比發現,移動支付的人數一直比公交卡支付的人數多。且在統計范圍的28天之內,共計多出1440824人。
3 邏輯回歸與混淆矩陣檢驗
邏輯回歸是將線性函數的結果映射到了Sigmoid函數中,Sigmoid函數如圖1:
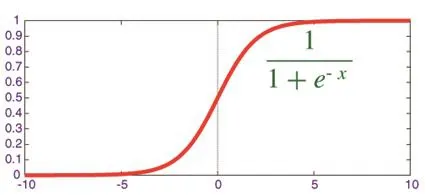
圖1 Sigmoid函數
其中x為樣本輸入,對應的函數為模型輸出,可以理解為某一分類的概率大小。而θ為分類模型的要求出的模型參數。對于模型輸出,令其讓它和二元樣本輸出y(假設為0和1)有以下的對應關系:如果模型輸出值大于0.5,則y為1。
混淆矩陣是一個兩行兩列的情形分析表,可以用來對分類器進行評估檢驗。矩陣的每一列表達了分類器對于樣本的類別預測,二矩陣的每一行則表達了版本所屬的真實類別,顯示以下四組記錄的數目:作出正確判斷的肯定記錄(真陽性)、作出錯誤判斷的肯定記錄(假陰性)、作出正確判斷的否定記錄(真陰性)以及作出錯誤判斷的否定記錄(假陽性)。
我們將用LSTM預測出的結果放入邏輯回歸分類器進行重復訓練,每天抽調出400個數據作為訓練集,100個作為測試集,對28天的數據分別進行檢驗。
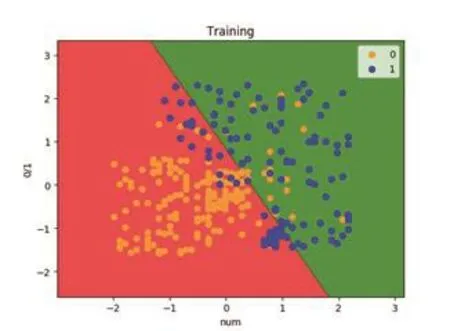
圖2 訓練集檢驗圖
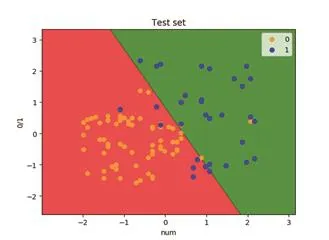
圖3 測試集檢驗圖
可知重復預測的結果比較理想,再根據混淆矩陣的輸出,以2月13日為例,當天一百個測試集的數據的混淆矩陣,得到矩陣打印結果:
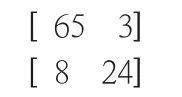
即成功率為89%,模型通過驗證。
4 結束語
綜合來看,移動支付平臺由四分之一到全部開放的過程中,增加了一定的固定成本,更關鍵的是移動支付客流量的大幅增長,經過代入數值計算,可得該城市在全部移動支付平臺投入運行后的第13天開始盈利,且第三方支付平臺在每位用戶處獲利0.5%,由于移動支付的客流量增大,故開始盈利三十天內,利潤可達到340000元。

