運動手環中的姿態檢測方法研究

宋 藝 張 波 唐芳月 劉師橋 劉語涵 王豐林

（天津師范大學計算機與信息工程學院,天津 300387）

1 引言

在信息技術高速發展的時代背景下,由于可穿戴式檢測裝置具有體積小、方便攜帶、低耗能等特點[9],因此越來越受人們的喜愛。

雖然可穿戴設備的外觀在人們的選擇考慮因素方面占有一定比例,但在更大程度上是對設備檢測準確性的選擇。因此從算法角度分析,如何提高對人體運動姿態檢測的準確性就顯得尤其重要。

如今市面上的手環大多數是無法精確檢測人的運動姿態,只能是通過“三軸加速度傳感器”來采集運動數據,簡單地記錄人是靜止的還是運動的。然后再通過算法對采集的數據進行處理分析,對比事先建立好的模型來判斷佩戴者的運動狀態。因此算法的好壞直接影響到檢測佩戴者狀態的準確性,所以在手環設計時選擇一個較為恰當的算法至關重要。

2 余弦測度

2.1 硬件選擇

該方法在硬件方面采用的是三軸加速度傳感器,該傳感器可以獲得三維立體空間的三個分量上的加速度信號,且該傳感器功耗低、體積小,對大多數手環均適用。

2.2 方法實現

假設空間中有兩個向量 a（x11,x12,...,x1n）和 b（x21,x22,...,x2n）,夾角余弦的具體計算公式如（1）所示。

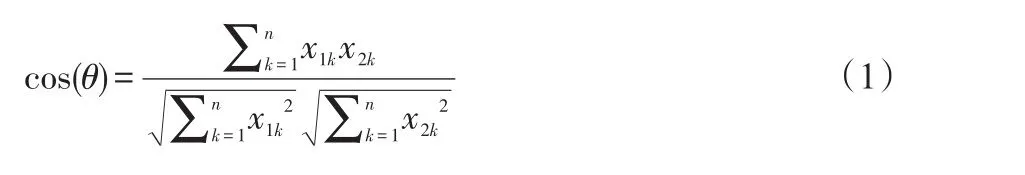
余弦測度主要是用于判斷兩種姿態的相似度,通過計算空間中兩個向量的夾角余弦來判斷兩個姿態的相似程度,當計算的數值小于某一臨界值時,可以認為是同一種姿態[1]。同時,可以通過滿足閾值時間點前后加速度矢量的過程來判定是否跌倒[7]。

通過這種方法,可以對確定臨界值的大小進而對姿態判斷的精確度進行提高,但臨界值不能定得過低,這樣就會導致很少甚至沒有同一種相同的姿態產生,導致了大量的冗余計算。

3 四元數算法

3.1 硬件選擇

該算法所選用的姿態模塊硬件是三軸加速度傳感器和三軸陀螺儀。

3.2 方法實現

四元數算法將陀螺儀獲得的角度信息融合到加速度傳感器中,進而得到精確的姿態判斷。

四元數 q可以用q0,q1,q2,q3來表示成一個復數,其中q0為四元數的實部,q1,q2,q3為四元數的虛部,四元數可表示為公式（2）,其中四元數q求模要滿足公式（3）。

四元數微分方程為公式（4）,其中ω為[0 ω1ω2ω3],而ω1,ω2,ω3為陀螺儀輸出的角速度。通過計算四元數微分方程,可以對四元數進行更新,使姿態判斷的準確性提高[2]。而針對于旋轉運動的旋轉四元數算法僅適用于低速旋轉狀態的判定[10]。

在運動加速度、磁場干擾等的影響下,短時間內精確度較低,這時可使用互補濾波方法對傳感器信息進行融合[5]。即與下述的WHPDS相結合而成的姿態檢測算法。

4 自適應波峰檢測

4.1 硬件選擇

慣性 EMES（Micro Electro Mechanical systems,即微電子機械系統）傳感器具有高質量、高靈敏度、重量輕、價格低廉等特點[2],因此被廣泛運用到重力加速度的測量方面,而該算法針對于MEMS傳感器姿態檢測和運動狀態的變化有較強的適應性。

4.2 方法實現

該方法是一種將波峰檢測計步算法和自相關分析計步算法相結合的判斷姿態的方法,通過單軸加速度和固定閾值對不同的運動狀態進行判斷。

該算法利用波峰檢測計步算法中不同姿態的幅值和步頻不同,再利用相應的閾值區間判斷運動姿態,圖1為自適應波峰檢測算法流程圖[3]。

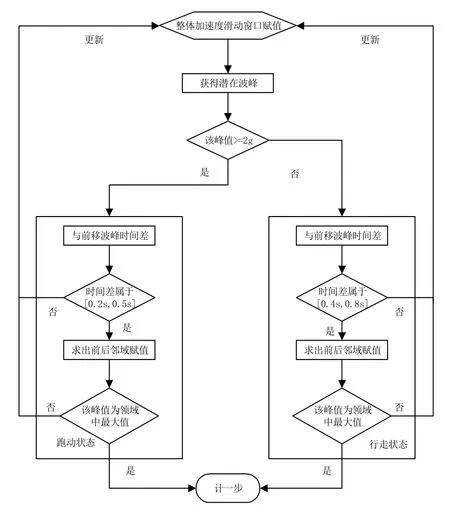
圖1 自適應波峰檢測算法流程圖

5 人體姿態檢測系統（WHPDS）

5.1 硬件選擇

該檢測系統所選用的硬件部分是六軸慣性傳感器,其集成一個三軸加速度傳感器和一個三軸陀螺儀。加速度計模塊可以識別靜止或平緩運動狀態下的角度信息,陀螺儀模塊對各種運動狀態下角度信息的變化均比較敏感[4]。

5.2 方法實現

WHPDS通過加速度計和陀螺儀獲得相應的姿態數據,利用互補濾波原理在短時間內對陀螺儀的角度進行最優化,然后得出佩戴者相應的姿態[6]。由于在短時間內陀螺儀所測量出的數據比較準確,而在長時間的檢測中加速度計所測量的數據比較準確,通過互補濾波使信號更加精確,進而使姿態判斷更加精確。

6 算法對比

以上的四種計算佩戴者姿態的方法均是對檢測數據增加精確度的姿態判斷方法,可以從上面的分析中看出,在硬件方面都用到了加速度傳感器,除了余弦測度以外都使用到了陀螺儀。可見大部分主流手環還是以加速度傳感器和陀螺儀為基本元件進行姿態檢測的。

余弦測度只用了一個三軸加速度傳感器進行姿態判斷,利用數學上簡單的余弦定理進行姿態種類是否相同的判斷。該方法計算簡便且硬件方面消耗較小,但在臨界值確定時要把握好度,同時,該方法需要前期大量的數據支持。

四元數算法是將加速度傳感器與陀螺儀進行聯系,通過對比重力向量的數值得出相應的姿態判斷。四元數算法雖然在硬件上增加了陀螺儀,但通過兩個部件得出的姿態判斷將更加準確,四元數算法是一種比較綜合的姿態檢測方法。

自適應波峰檢測是由波峰檢測計步算法和自相關分析計步算法相結合的姿態判斷算法,它和其他三種算法都不太相同,通過不同運動狀態的幅值和步頻不同進而判斷出不同的運動姿態。自適應波峰檢測的優點在于計算量小,可以方便地進行實時檢測[10],適用于行走或跑步之類的計步的姿態判斷,但并不適用于具體姿態的判斷。

WHPDS也是運用加速度傳感器和陀螺儀進行姿態檢測的,與四元數算法不同的是它利用互補濾波進行姿態判斷,得出的判斷較為精確,但它需要多個傳感器在人體不同位置記錄數據,對那些需要精確記錄行動狀態的病人是有很大幫助的。

7 結論

通過上述對四種姿態判斷方法的分析與比較,可以看出不同的方法各有特點,如何選用不同的方法需要根據情況而定。

設計兒童手環并不需要過于精確的運動姿態判斷,而且根據兒童相對比較多動,因此不適用于在身體不同位置安置多個傳感器,所以在設計兒童手環時WHPDS可以略去,不予采用。

因此,在設計兒童手環時應采用以四元數算法為主體,余弦測度和自適應波峰檢測為輔的綜合算法對姿態進行判斷,硬件方面采用三軸加速器和陀螺儀相結合的傳感器。自適應波峰檢測先對運動姿態進行較快的判斷,主要用于實時數據的更新,然后使用四元數算法對自適應波峰檢測出的結果進行檢測,得出精確的姿態判斷。

[1]王壯.可穿戴設備中的人體姿態識別方法[D].南京:南京郵電大學,2016.

[2]李炳炳.基于M EM S慣性傳感器的人體姿態檢測系統的研究[D].南京:南京理工大學,2017.

[3]陳國良,李飛,張言哲.一種基于自適應波峰檢測的M EM S計步算法[J].中國慣性技術學報,2015,23(03):315-321.

[4]胡小華,李向攀,祁洋陽,等.可穿戴式人體姿態檢測系統設計[J].電子技術應用,2017,43(09):13-16.

[5]李景輝,楊立才.基于多傳感器信息融合的人體姿態解算算法[J].山東大學學報(工學版),2013,43(05):49-54.

[6]郭曉鴻,楊忠,陳喆,等.EK F和互補濾波器在飛行姿態確定中的應用[J].傳感器與微系統,2011,30(11):149-152.

[7]孫新香.基于三軸加速度傳感器的跌倒檢測技術的研究與應用[D].上海:上海交通大學,2008.

[8]陳國良,張言哲,楊洲.一種基于手機傳感器自相關分析的計步器實現方法[J].中國慣性技術學報,2014,22(06):794-798.

[9]陳功.基于三軸加速度傳感器的跌倒檢測技術的研究與應用[D].南京:南京郵電大學,2013.

[10]王彤,馬建倉,秦濤,等.基于旋轉四元數的姿態解算算法[J].彈箭與制導學報,2014,34(03):15-16.