一種OFDM聯合峰均比抑制算法

李　波,鄭　晨,王彥本

(西安郵電大學 通信與信息工程學院,陜西 西安 710121)

正交頻分復用(orthogonal frequency division multiplexing,OFDM)采用相互正交的子載波傳輸信號，能夠提高數據傳輸速率，抵抗無線信道多徑傳輸帶來的頻率選擇性衰落[1]。自20世紀50年代出現至今，OFDM技術廣泛應用于高比特率數字用戶線系統，數字音頻廣播系統和長期演進等系統中[2]。

信號的高峰均功率比(peak to average power ratio,PAPR)是OFDM技術應用所面臨的難題之一。當多個子載波上的信號出現同相疊加時，會產生超出大功率放大器(high power amplifier,HPA)線性工作范圍的尖峰信號，引起信號的畸變和頻譜的擴散。現有的主流的峰均比抑制方法包括削波限幅[3]、選擇映射(selected mapping,SLM)[4]、主動星座擴展(active constellation extension,ACE)[5]、部分序列傳輸(partial transmit sequences,PTS)[6]、壓擴變換(companding)[7]和載波預留(tone reservation,TR)[8]等。其中預留子載波技術只使用一部分子載波傳輸數據，其余的子載波被預留出來，專門傳輸用于抑制峰均比的削峰信號。由于傳輸數據的子載波和存放削峰信號的子載波相互正交，因此削峰信號不會對數據信號造成干擾。在接收端，削峰信號可以被直接濾除，而不需要發送任何邊帶信息。

經典的預留子載波峰均比抑制算法中，限幅噪聲比(signal to clipping noise ratio-tone reservation,SCR-TR)算法通過使限幅噪聲功率比SCR取值最小，設立優化目標，推導PAPR抑制算法的迭代公式；通過工程優化理論，僅選取最大峰值進行處理，有效降低了算法復雜度，并可防止過度削峰帶來的帶外譜噪聲，但算法收斂速度緩慢[9]。

本文針對預留子載波峰均比抑制技術算法收斂速度慢、抑制效率低的問題，研究PAPR抑制問題的凸優化建模和迭代過程的懲罰函數表達式；構建基于預留子載波的聯合峰均功率比迭代過程；設計各懲罰函數項的加權組合，分析算法的合理性，并通過仿真驗證該算法的PAPR抑制性能、誤碼率和帶外頻譜擴散性能。

1　OFDM系統的預留子載波技術

下面給出基于預留子載波技術的OFDM發射系統原理及峰均功率比的定義。

1.1　預留子載波技術原理

基于預留子載波技術的OFDM系統發射系統原理，如圖1所示。

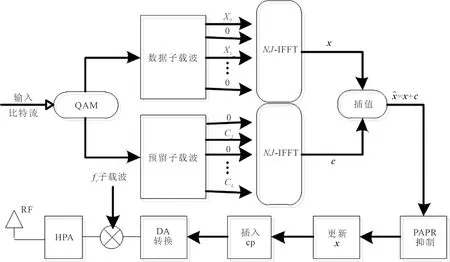
圖1　基于預留子載波技術的OFDM發射系統原理

圖1中，輸入的比特流經過正交振幅調制(quadrature amplitude modulation,QAM)方式調制后，生成頻域信號

X=[X0,X1,…,XN-1]T。

數據子載波負責承載頻域信號數據X，而預留子載波負責承載頻域削峰信號C。J倍過采樣后的信號通過NJ快速傅里葉逆變換(inverse fast Fourier transform,IFFT)運算轉換為時域信號

x=[x1,x2,…,xn,…,xNJ]T。

同理，得到時域消峰信號

c=[c1,c2,…,cn,…,cNJ]T。

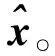
設OFDM系統的子載波總數為N，預留子載波總數為L，過采樣率為J。圖1中經過NJ點IFFT運算后的時域數據信號可以表示為

其中n=1,2,…,NJ,所以上式可以改寫為

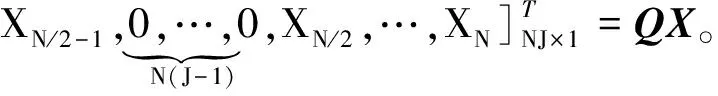
其中，j表示虛數單位，xn為n時刻的OFDM時域信號，Xk是QAM調制后的頻域信號的第k個元素(k=1,2,…，NJ)，Q為傅立葉變換矩陣，Q矩陣的第m行n列(m,n=1,2,…，NJ)元素為

其中QJ是將矩陣Q中間的N(J-1)個全零列去掉后所得到的NJ行n列子陣。

1.2　峰均功率比的定義

OFDM信號峰均功率比定義為OFDM信號最大峰值功率與平均功率之比，OFDM信號的峰均功率比

其中，E[]表示數學期望。在衡量各類算法抑制OFDM信號峰均功率比的效果時，常采用互補累積分布函數(complementary cumulative distribution function,CCDF)來刻畫。CCCDF是OFDM信號的峰均功率比超過指定門限值PPAPR(obj)的概率，定義為

CCCDF(PPAPR(obj))=Pr{PPAPR>PPAPR(obj)}。

2　聯合峰均功率比抑制算法

下面給出本文所提出的聯合峰均功率比抑制算法的原理和步驟。

2.1　聯合峰均功率比抑制算法的原理

經過削波限幅算法[9]處理后的信號可表示為

本文所提出的聯合峰均功率比抑制算法是基于凸優化建模構建的[10]，聯合算法J可以通過3個變量表示為

其中β為縮放因子，g(·)為階躍函數，λ為罰因子，NJA為罰函數。

在限幅噪聲比(SCR-TR)算法[9]中

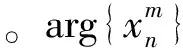
在最小平方逼近(least square approximation-tone reservation,LSA-TR)算法[11]中，

xm+1=xm+μcm。

其中μ和cm可分別看作是LSA-TR算法的罰因子和罰函數。cm是第m次迭代后的時域預留子載波信號。罰因子μ是依據最小平方法計算得出的，從而使μcm能夠在峰值出現位置盡可能地逼近限幅噪聲的幅度。

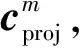
聯合峰均功率比抑制算法的原理，如圖2所示。

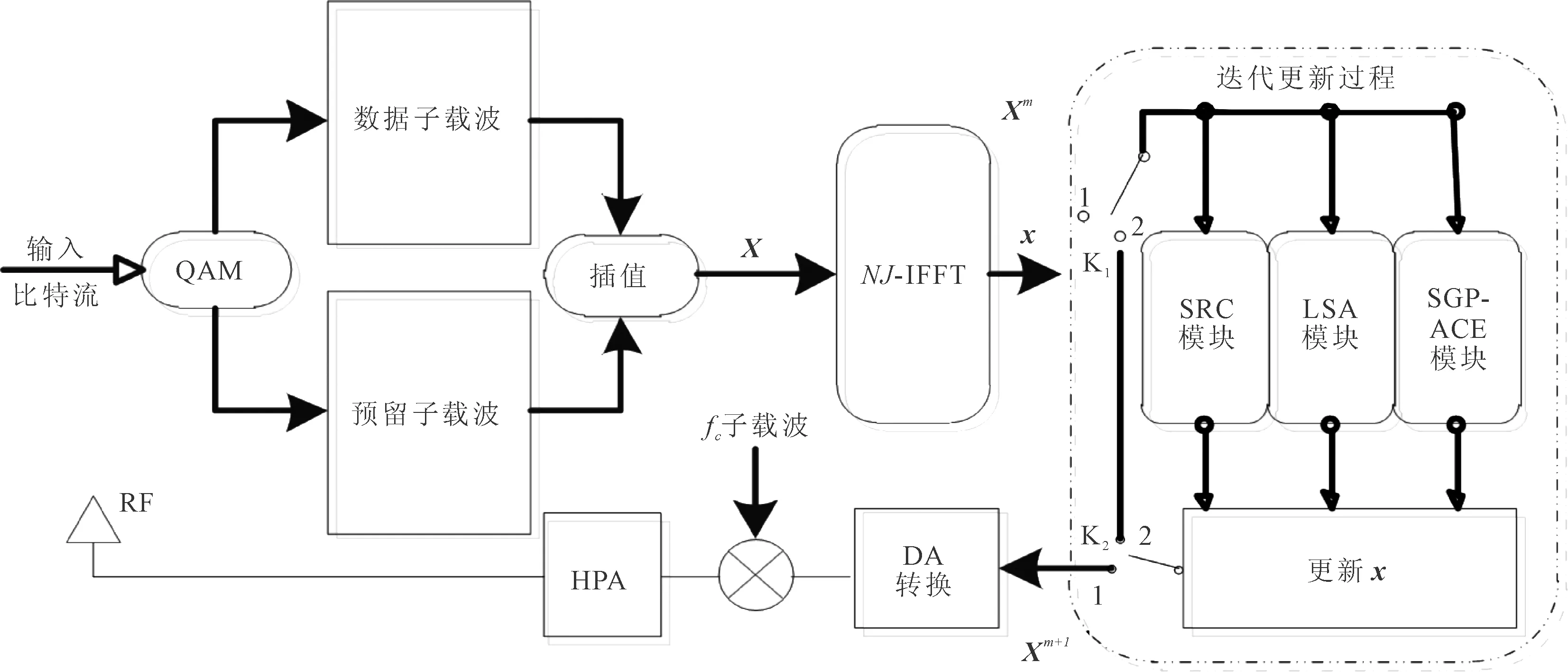
圖2　聯合峰均功率比抑制算法原理

2.2　算法步驟

所提出的聯合峰均功率比抑制算法的主要步驟總結如下。

步驟1初始化設置。設定峰均功率比抑制目標值PPAPR(obj)，子載波總數N，預留子載波總數L，最大迭代次數Mmax和限幅門限A。時域信號的初始值為x0，峰均功率比初始值為PPAPR(0)。

步驟2將輸入信號轉換為頻域信號X。將預留子載波上的信號初始化為零。經過數據子載波和預留子載波的插值操作后，對X進行NJ點的IFFT運算生成時域信號x。將開關K1置于1，K2置于2，開始迭代運算，此時m=1。

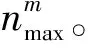
步驟4計算限幅噪聲fm=ym-xm。對fm做NJ點的傅里葉變換(fast Fourier transform,FFT)運算，生成Fm。將Fm數據子載波上的信號置為零，從而得到頻域削峰信號Cm。Cm經NJ點的IFFT運算轉換為時域削峰信號cm，即為LSA-TR方法中的懲罰函數。

步驟5計算LSA-TR方法中的罰因子

步驟6將Fm預留子載波上的信號置為0，并將得到的頻域數據信號進行主動星座擴展修正。

步驟7計算cm在xm上的投影值，得到投影系數

其中

步驟8計算SGP-ACE方法中的罰因子

其中元素表示為

步驟9用LSA-TR和SGP-ACE方法中的罰因子分別乘以各自的罰函數，并與SCR-TR方法一起加權組合，構成迭代公式，得到xm+1。其中SCR-TR方法的迭代步長選取LSA-TR方法中的罰因子μm。各算法在加權迭代過程中的權值(縮放因子)可由仿真實驗調整。

步驟10計算xm+1的峰均功率比數值PPAPR(m+1)。若PPAPR(m+1)已經達到或超過PPAPR(obj)，停止迭代。如果迭代次數大于Mmax，停止迭代。迭代停止時，將K2置于1，輸出xm+1。否則，迭代次數加1，返回第3步，繼續進行迭代運算。

3　仿真結果及分析

通過Matlab仿真，比較分析所提出的聯合峰均功率比抑制算法的峰均功率比抑制性能、誤碼率及帶外頻譜擴散性能。

在以下各種仿真模型中，均設定OFDM系統中的子載波數N=1 024，其中預留子載波數L=54。OFDM符號數為1 000，過采樣率J=4。針對過采樣后的OFDM時域信號，設定削波門限A=2E{|xm|}。星座調制方式分別采用正交相移鍵控(quadrature phase shift keyin,QPSK)或正交幅度調制(quadrature amplitude modulation,16QAM)。無線信道模型分別選取高斯信道(additive white Gaussian noise,AWGN)模型或萊斯(Rician)信道模型。

3.1　聯合峰均功率比抑制算法的抑制效果

所提出的聯合峰均功率比抑制算法和其他6種基于預留子載波技術的經典峰均功率比抑制算法的PAPR抑制性能進行了對比。

這幾種經典算法分別是：凸集投影(projections onto convex scts-tone reservation，POCS-TR)算法[13]、削波限幅(clipping-TR)算法[9]、限幅噪聲比(SCR-TR)算法[9]、主動星座擴展(active-set)算法[14]、最小平方逼近(LSA-TR)算法[11]和智能梯度投影主動星座擴展(SGP-ACE TR)算法[5]。峰均功率比抑制性能比較，如圖3所示。

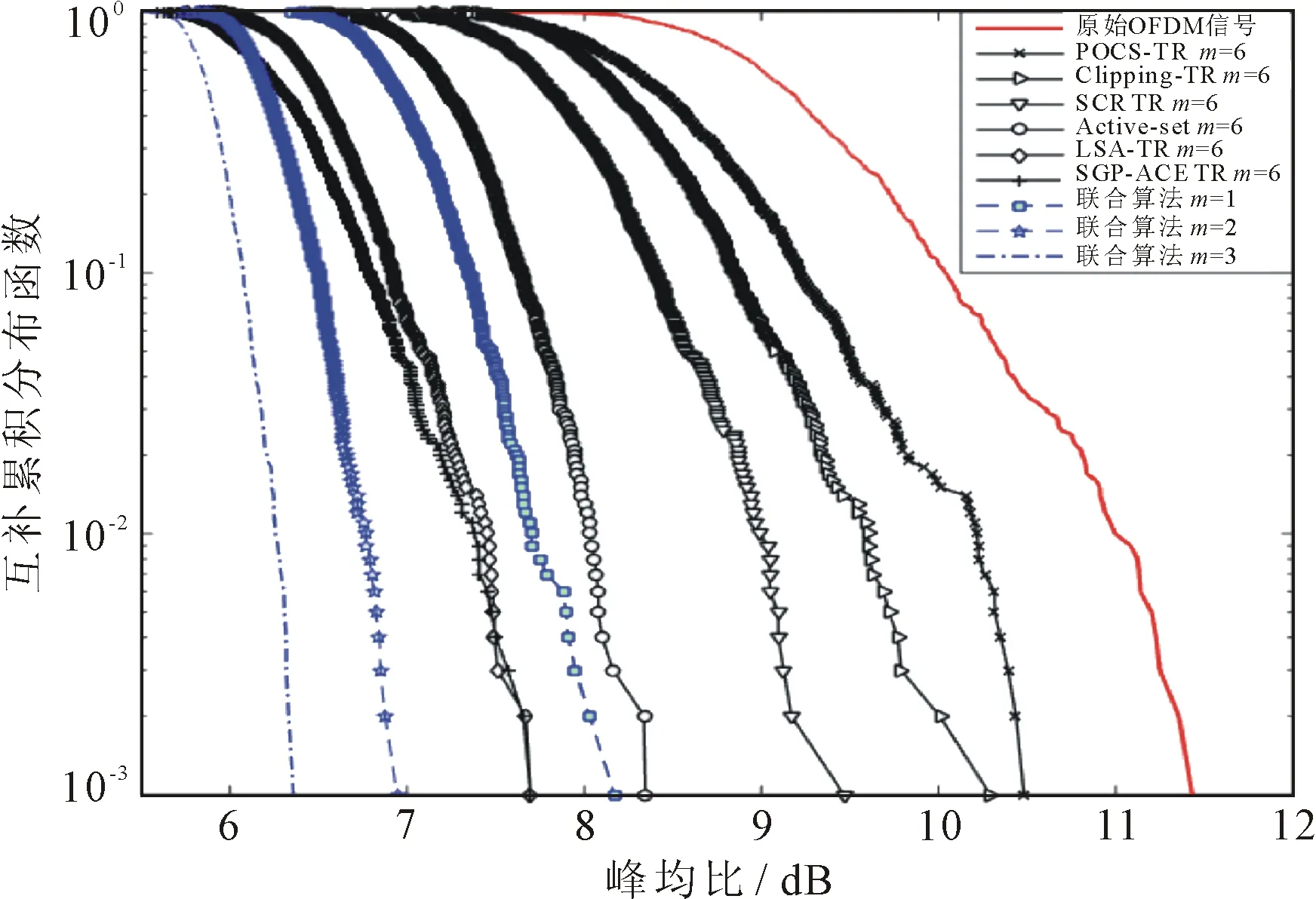
圖3　峰均功率比抑制性能比較

如圖3所示，仿真中同時給出了原始OFDM信號的峰均功率比互補累積分布函數(CCDF)曲線，從而可以清晰地觀察不同算法的峰均功率比抑制效果。

如圖3所示，僅經過1次迭代運算(m=1)，所提出的聯合峰均功率比抑制算法的峰均功率比的抑制性能已經優于POCS-TR、Clipping-TR、SCR-TR和active-set這4種算法各自經過6次迭代運算(m=6)所達到的抑制效果。所提出的聯合峰均功率比抑制算法經過2次迭代運算(m=2)后的峰均功率比抑制性能優于LSA-TR和SGP-ACE TR算法分別經過6次迭代運算所能達到的抑制效果。經過3次迭代運算(m=3)后，所提出的聯合峰均功率比抑制算法在CCCDF=10-3時，峰均功率比抑制能力可以達到6.359 dB。在相同峰均功率比抑制性能的要求下，所提出的聯合峰均功率比抑制算法需要的迭代次數明顯小于其他6種經典子載波預留算法。

3.2　聯合峰均功率比抑制算法的誤碼率比較

所提出的聯合峰均功率比抑制算法與3中經典算法的誤比特率(bit error ratio,BER)在高斯信道(additive white Guassian noise，AWGN)和QPSK星座調制方式下比較，如圖4所示。

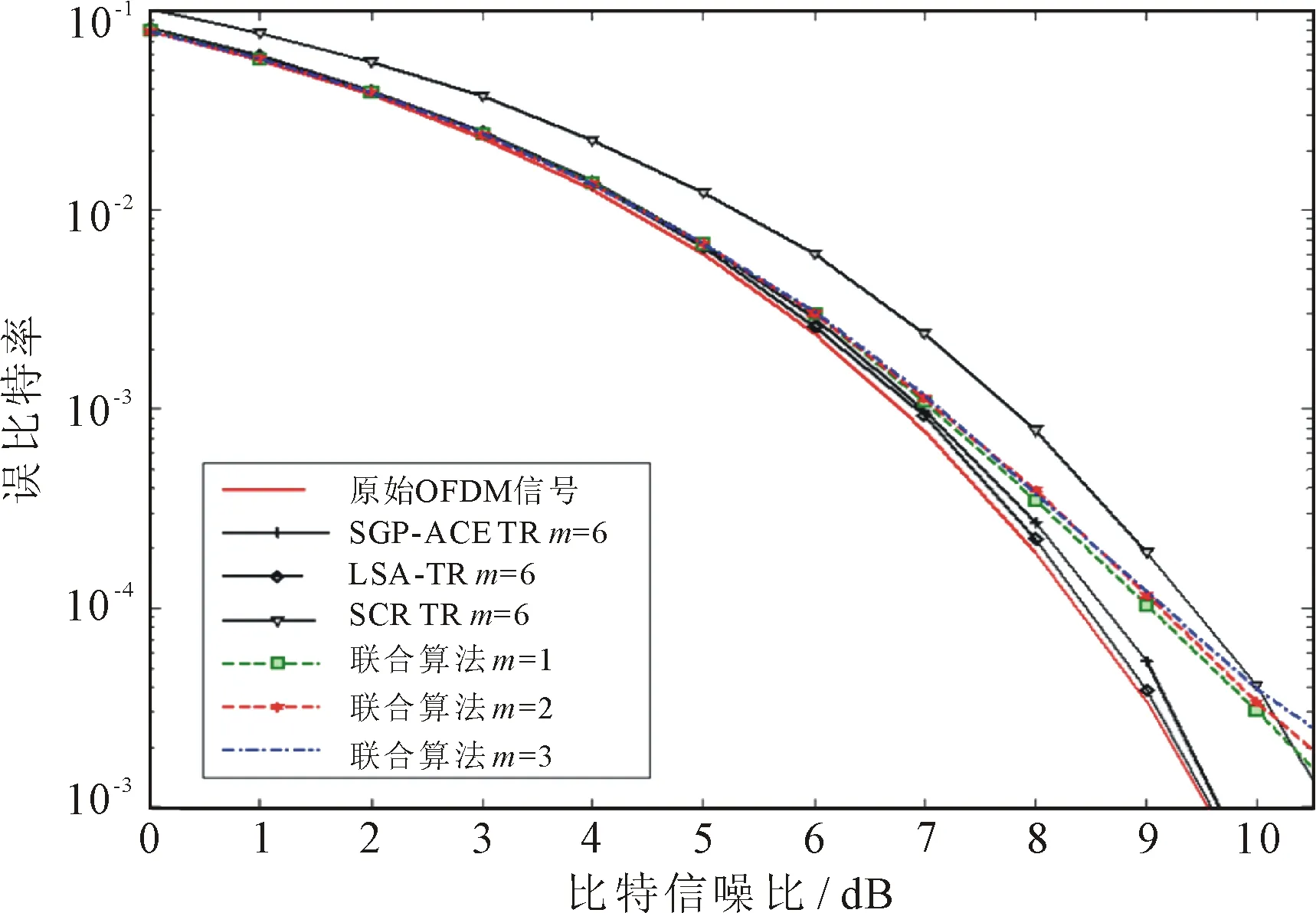
圖4　高斯信道下的誤比特率比較

如圖4所示，所提出的聯合峰均功率比抑制算法在分別經過1、2、3次迭代后的BER曲線幾乎重合在一起。迭代次數的增加并不會明顯惡化BER性能。當比特信噪比小于7 dB時，所提出的聯合峰均功率比抑制算法的BER性能與SGP-ACE TR和LSA-TR算法經過6次迭代后的BER曲線幾乎重合。當比特信噪比大于7 dB小于10 dB時，所提出的聯合峰均功率比抑制算法的BER性能開始下降，但仍然優于SCR-TR算法的BER性能。

不同峰均功率比抑制算法在16QAM星座調制方式下對比，如圖5所示。

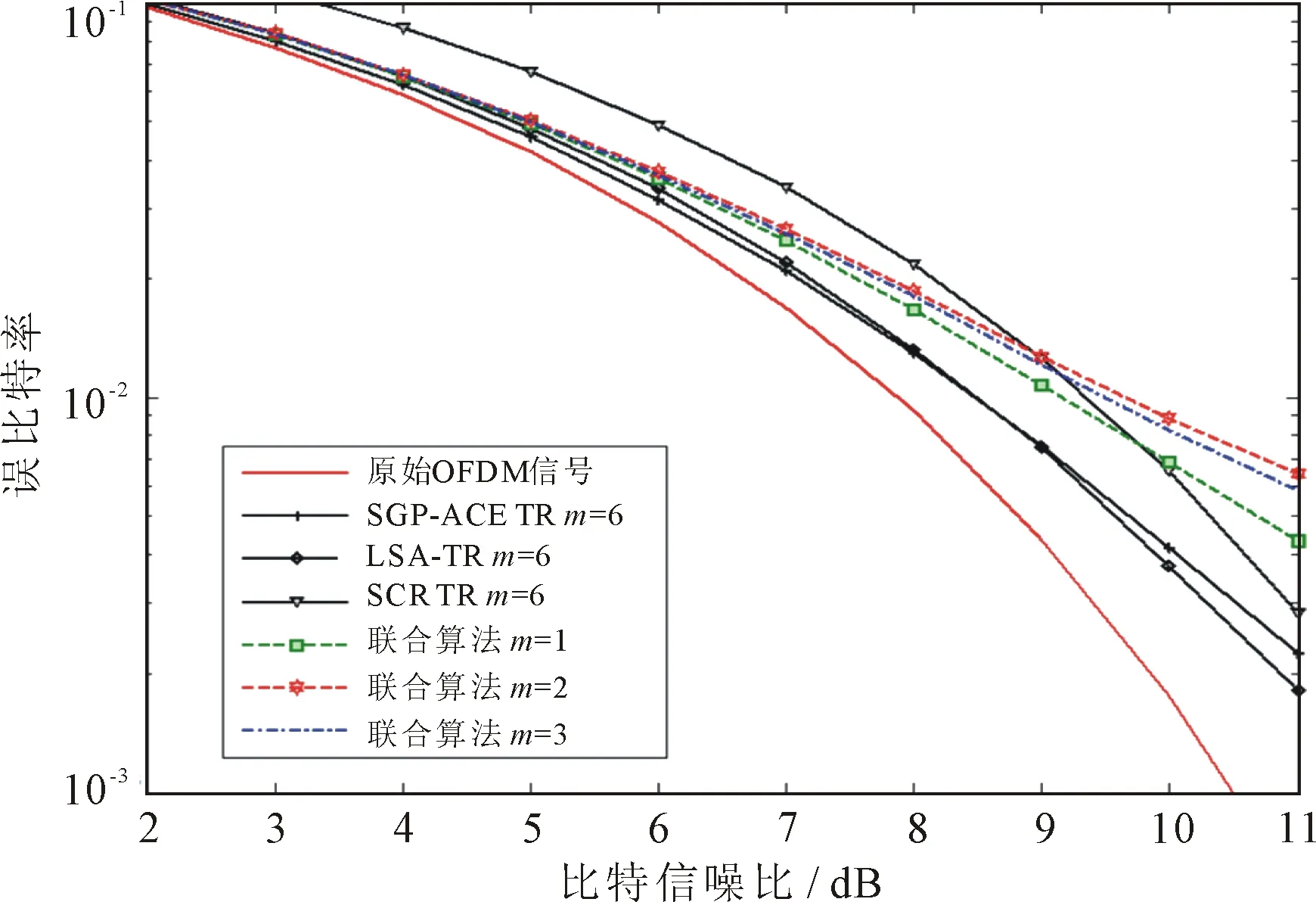
圖5　高斯信道的誤比特率比較(16QAM)

通過高斯信道(AWGN)后的誤碼率曲線。所提出的聯合峰均功率比抑制算法的誤比特率(BER)隨迭代次數的增加，沒有明顯的惡化。第3次迭代后的BER性能甚至略優于第2次迭代的BER性能。與其他3種經典算法相比，當比特信噪比小于9 dB時，聯合峰均功率比抑制算法仍優于SCR-TR算法的BER性能。對比圖3可知，聯合峰均功率比抑制算法能夠用BER性能的略微下降換取峰均功率比抑制效果的顯著提高。

不同峰均功率比抑制算法在QPSK星座調制方式下，通過萊斯信道(Rician)后BER特性如圖6所示。

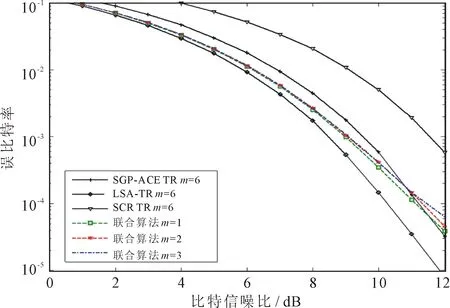
圖6　萊斯信道下的誤比特率比較

當信噪比小于11 dB時，所提出的聯合峰均功率比抑制算法在迭代1、2、3次后的BER性能優于SGP-ACE TR和SCR-TR算法各自迭代6次后的BER性能。迭代次數的增加并不會造成聯合峰均功率比抑制算法的BER性能明顯惡化。

3.3　聯合峰均功率比抑制算法的功率譜密度比較

分別經過所提出的聯合峰均功率比抑制算法和其他3種經典PAPR抑制算法優化后，OFDM信號的功率譜密度(power spectral density,PSD)曲線，如圖7所示。

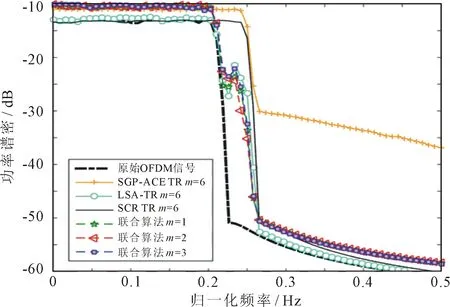
圖7　不同算法在QPSK調制下的功率譜密度比較

PSD曲線的“帽檐”越高，說明該算法的頻譜擴散越嚴重。為了便于比較，同時給出了原始OFDM信號的PSD曲線。由圖7可見，SGP-ACE TR算法的帶外頻譜擴散性能最差。所提出的聯合峰均功率比抑制算法經過1、2、3次迭代處理后的PSD性能接近SCR-TR和LSA-TR算法，且明顯優于SGP-ACE TR算法。

4　結語

本文提出基于預留子載波的聯合峰均功率比抑制算法，研究該算法的峰均功率比抑制性能與誤碼率、帶外頻譜擴散性能的相互折衷。本文的主要貢獻在于：

(1)參照峰均功率比抑制問題的凸優化建模和懲罰函數表達式，對多種經典子載波預留算法進行理論分析，找出每種算法能夠使迭代過程快速收斂的懲罰函數。

(2)對SCR-TR、SGP-ACE TR和LSA-TR的峰均比抑制懲罰函數進行加權組合，生成聯合峰均功率比抑制算法的迭代過程。

(3)通過仿真實驗分析聯合峰均功率比抑制算法的峰均功率比抑制效果。評估該算法高性能的峰均功率比抑制效果與誤碼率和帶外頻譜擴散性能之間的折衷。

(4)對比聯合峰均功率比抑制算法與其他經典峰均功率比抑制算法的各項性能。

通過實驗分析，聯合峰均功率比抑制算法僅需2次迭代，便可以超越其他經典算法經過6次迭代才能達到的峰均功率比抑制效果。由迭代次數大幅下降所節省的優化時間較為可觀。聯合峰均功率比抑制算法的BER性能在比特信噪比相對較小的信道環境中更具優勢。該算法的帶外頻譜擴散性能沒有明顯的惡化。