基于雙曲正弦函數的改進變步長自適應濾波算法
程建民,張潤蓮,2,秦明峰
(1.桂林電子科技大學 廣西無線寬帶通信與信號處理重點實驗室,廣西 桂林 541004; 2.廣西高校云計算與復雜系統重點實驗室,廣西 桂林 541004; 3.衛星導航系統與裝備技術國家重點實驗室,河北 石家莊 50081)
0 引言
在傳統的LMS(Least Mean Square)算法[1]中,為提升算法的收斂速度,應該盡可能選擇較大的步長值;而為了減小算法的穩態誤差,應該盡可能選擇較小的步長值。這一矛盾使得傳統的LMS算法必須在這二者之間進行折中處理,導致算法性能不理想。
為解決該問題,研究者們在基于步長因子調整原則的基礎上,通過改變步長因子的表現形式來改進LMS算法的性能,經典的算法有基于對數函數[2]、基于雙曲正弦函數的變步長LMS算法[3]和固定步長算法[4]等,但均存在步長值與穩態誤差之間的矛盾。針對該矛盾,文獻[4]通過結合Sigmoid函數和正弦函數對步長因子進行調節控制;文獻[5]通過引入反饋控制函數建立步長因子與誤差信號的非線性函數模型改進LMS算法,兼顧收斂速度和穩態誤差性能;文獻[6]通過引入雙曲正切函數控制步長因子,提高算法的抗噪聲能力;文獻[7-8]通過權系數的變化來控制步長因子的變化,以保證當系統達到穩態時停止迭代;文獻[9]通過調整抽頭長度的方式,獲取最優維納解。上述算法在收斂速度和穩態誤差方面有所改進,但計算量相對較高。
針對上述問題,本文給出了一種基于雙曲正弦函數形式的改進LMS算法,該算法通過引入線性函數與步長函數相乘,改變步長函數特性,實現對步長值的自適應控制,提升收斂速度,降低算法復雜度,提高抗噪能力。
1 相關算法及分析
1.1 LMS算法
LMS算法是線性自適應濾波器算法,是一種以最小均方誤差準則(Minimum Mean Square Error,MMSE)為設計準則的瞬時值估計梯度矢量的方法,使濾波器的輸出信號與期望響應之間的均方誤差達到最小。自適應濾波器的濾波原理如圖1所示。
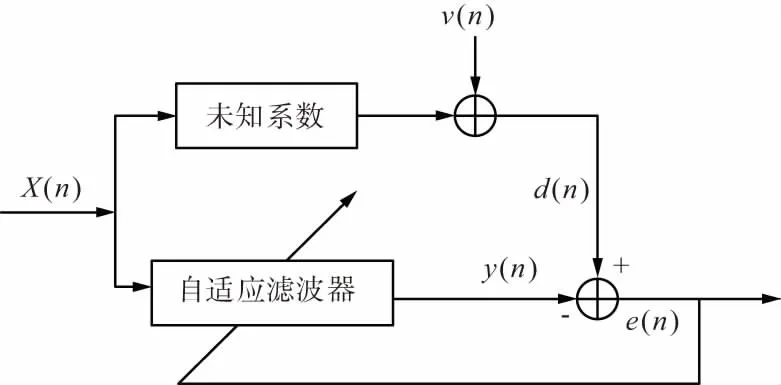
圖1 自適應陷波器基本原理
圖1中,X(n)、v(n)、d(n)、y(n)、e(n)分別為實際輸入信號、噪聲信號、期望信號、輸出信號及誤差信號。LMS算法步驟為:
① 權值系數初始化:W(0)=0;
② 濾波器的輸出:y(n)=WT(n)×X(n);
③ 濾波器n時刻的誤差:e(n)=d(n)-y(n);
④ 抽頭權向量:W(n+1)=W(n)+μ×e(n)×X(n);
⑤ 重復步驟②~④,直到W(n+1)的值趨于穩定。
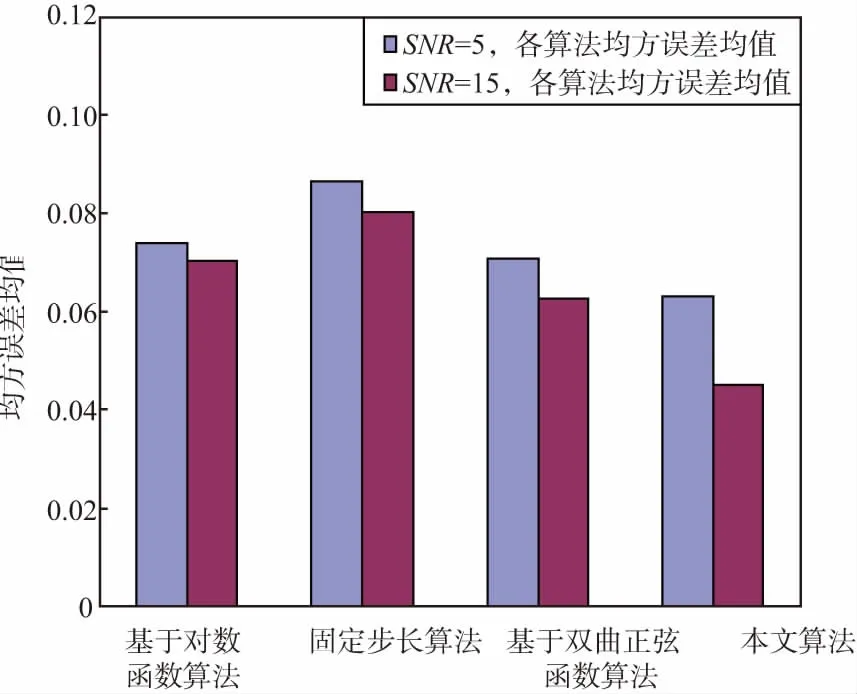
其中步長因子u對LMS算法的性能起著決定性的作用,其收斂的條件是:0 為了使LMS算法的收斂速度、穩態誤差和抗噪聲能力均能取得較好的性能表現,下面給出幾種常用的LMS算法,如基于對數函數、基于雙曲正弦函數的變步長LMS算法和固定步長算法,各算法的步長因子和誤差信號關系曲線如圖2所示。 圖2 e(n)和u(n)關系曲線 1.2.1基于對數函數的變步長LMS算法 文獻[2]在對數函數y=loga(x)的基礎上對其進行變化調整,建立了步長因子u(n)與誤差信號e(n)之間的關系表達式: μ(n)=a×lg[b×|e(n)c|]。 (1) 由圖2可知,e(n)為時0,u(n)不為0,存在誤差;而且當e(n)趨近于0時,函數底部變化太快,這會導致步長因子錯過最佳值;同時,該算法存在指數運算,計算復雜度較高。 1.2.2基于雙曲正弦函數的變步長LMS算法 文獻[3]在雙曲正弦函數y=sinh(x)=(ex-e-x)/2的基礎上,其進行變換調整,建立了步長因子u(n)與誤差信號e(n)之間的關系表達式: μ(n)=a×|sinh[b×e(n)c]|。 (2) 由圖2可知,當e(n)較大時,u(n)變化較快;當e(n)趨近于0時,函數底部變化太緩慢,即誤差信號不為0時u(n)已經為0,造成了較大的穩態誤差;同時該算法存在指數運算,計算復雜度較高。 1.2.3固定步長LMS算法 固定步長LMS算法,其步長值在算法迭代過程中為一個固定值,據文獻[4]可知,一般取u=0.01;由圖2可知,無論當前系統的誤差值如何變化,步長值u一直維持不變,即固定步長。 文獻[7]中提出了步長因子u調整原則:在自適應參數發生變化時或者算法的起步收斂階段,應該使步長值u較大,使得算法具有較快的收斂速度;而在算法達到收斂后,此時系統的權值矢量已接近最優值,步長值u應該維持很小的值,以達到很小的穩態誤差。在滿足步長因子調整原則的基礎上,LMS算法收斂速度越快,效率越高;收斂深度越深,穩態誤差越小。因此,收斂速度和穩態誤差是改進LMS算法的主要方向,也是判定算法性能的重要指標。 基于步長因子的調整原則和算法性能需求,通過圖2分析可知,基于雙曲正弦函數形式控制的步長因子曲線相比其他算法更符合步長因子調整原則。由文獻[3]可知,基于雙曲正弦函數的變步長LMS算法形式簡單、計算量小,當u(n)與e(n)滿足一定函數關系時,算法的收斂速度和穩態誤差都能取得較好的表現。因此,本文采用雙曲正弦函數控制步長因子,并對其過早達到平穩狀態(即誤差信號e(n)不為0時,u(n)已經無限接近于0)這一缺點進行改進。 針對文獻[3]中算法存在的問題,本文改進思路如下:將步長值與迭代過程中的某種狀態變量相關聯,利用該狀態變量的動態變化來調整步長值的變化。其中,狀態變量可以是瞬時誤差、瞬時誤差的平方、相鄰2次迭代的瞬時誤差的相關函數[10]、誤差與輸入矢量的相關性[11]等。該狀態變量在開始收斂時較大,而在收斂后較小,因此滿足動態控制步長值的要求。 由于瞬時誤差e(n)相比其平方和其相鄰2次相關函數具有獲取容易、結構簡單、計算量小等優勢。因此,本文選用瞬時誤差信號e(n)作為狀態變量并與步長值相關聯,從而實現對步長值的動態調整。 根據函數f(x)=1+|x|性質可知,該函數關于y軸對稱,最小值為1。若將上述瞬時誤差作為函數f(x)=1+|x|的自變量,可得函數f[e(n)]=1+|e(n)+b|,其中,b用來調節函數曲線底部浮動幅度。將式(2)與該函數相乘,則變步長函數的曲線底部值增加,可以達到改變函數曲線底部特性的目的,防止其過早達到穩態。 此外,針對式(2),文獻[3]中的實驗測試表明,在指數c=1時,算法復雜度最低。因此,本文選取c=1,這使得函數f[e(n)]=1+|e(n)+b|與式(2)的乘積,去掉了指數運算,從而降低算法復雜度。改進的變步長函數表達式具體如下: μ(n)=a×|sinh[e(n)]|×[1+|e(n)+b|], (3) 式中,參數a用來調節曲線的幅值。改進的變步長LMS算法表達式為: 為驗證本文改進算法性能,使用Matlab2014仿真軟件,并采用文獻[12]中所列的實驗條件進行仿真實驗,測試算法的收斂速度、均方誤差、抗噪能力以及計算復雜度,具體條件如下: ① 二階自適應濾波器系統; ② 輸入信號X(n)是零均值、方差為1的高斯白噪聲; ③ 高斯白噪聲的方差為0.04、均值為0,且與輸入信號無關; ④ 實驗采樣點數N=500,未知系統的FIR系數為W=[0.8,0.5]T。 為減少實驗誤差,實驗將取200次仿真實驗數據的平均值,繪制其收斂曲線。 改進的變步長函數表達式(3)中的參數a可以調節函數曲線幅值的大小,若a值過小,算法在還未達到最小穩態誤差時,步長值已為零,將導致算法收斂速度過慢;若a值過大,算法曲線底部變化較快,會導致錯過最佳步長值。參數b調節函數曲線底部浮動幅度,若b值過大,可能導致函數曲線難以收斂,誤差較大;若b值過小,此時并不能對其過早達到穩態的這一不足進行優化。 根據文獻[13-14]及經驗認知,a和b的最佳取值范圍均為(0,1]。在實驗測試中,對a、b分別從0.1開始,以0.1步長增長組合測試算法的步長因子和誤差信號關系曲線,測試結果顯示,在a逼近0.1時,初始步長值較小,容易錯過最佳步長值;在a逼近1時,初始步長值較大,計算復雜度高。故令a=0.5,再測試b分別取不同值時的關系曲線,其顯示b太小時函數曲線底部變化太快,b太大則會產生突變,結果如圖3所示。 圖3 參數a與b組合取值的關系曲線 基于上述實驗對比,本文算法參數取值為a=0.5,b=0.5。 基于同樣的實驗條件,對比測試了本文改進算法與基于對數函數算法、基于雙曲正弦函數和固定步長因子算法的收斂速度和抗噪能力。基于對數函數算法中,取a=1 000、b=0.02、c=2;基于雙曲正弦函數中,a=0.006、b=5、c=1;固定步長因子算法中其步長因子取0.01。 3.3.1收斂速度測試實驗 文獻[15]表明,通過均方誤差和迭代次數的關系曲線可以較好地反映算法的收斂速度,算法最先達到穩態,且所需迭代次數最少,則其收斂速度最佳。基于上述選取的參數,各算法的測試結果如圖4所示。 圖4 4種算法收斂速度對比 圖4結果表明,固定步長算法由于其步長值固化,收斂速度最慢;基于對數函數算法,由于其對數函數性質,步長函數的變化太快,收斂較慢;基于雙曲正弦函數算法由于其存在指數運算,收斂速度較快。由式(3)可知,本文算法通過改變基于雙曲正弦函數算法的步長函數性質達到改進目的,其步長值大于雙曲正弦函數算法步長值,其收斂速度更快。 3.3.2抗噪能力測試實驗 由文獻[16]可知,均方誤差能夠評判算法的抗噪能力,在算法收斂的前提下,均方誤差越小,算法抗噪能力越好。基于上述實驗條件,在自適應濾波器的輸入信號中加入高斯白噪聲,使信號信噪比[17]SNR分別為5 dB和15 dB,將各算法500次迭代后產生的均方誤差值求其均值,測試結果如圖5所示。 圖5 4種LMS算法抗噪能力對比 圖5結果表明,信噪比越高,各算法抗噪能力越強。在SNR=5時,信噪比較低,各算法對噪聲均較為敏感,固定步長算法由于步長值固化,收斂速度慢,抗噪性能最差;基于雙曲正弦函數和對數函數算法的收斂速度均優于固定步長算法,達到穩態后,均方誤差均值相近,其抗噪能力均優于固定步長算法。在SNR=15時,信噪比較高,各算法的均方誤差均值明顯下降,符合通信理論基本原理。文獻[18-19]中指出,誤差信號中的噪聲自相關性一般較強,互相關性較差。本文算法利用噪聲較差的互相關性,使用步長函數將其去除,降低噪聲對步長的影響,使得本文算法在兩種信噪比下的均方誤差均值都最小,具有較好的抗噪能力。 本文介紹了幾種常用的變步長LMS自適應濾波算法,并針對基于雙曲正弦函數LMS自適應濾波算法過早達到平穩狀態及計算開銷[20]問題,給出了改進方法。該方法基于步長因子與瞬時誤差信號建立雙曲正弦函數關系,通過改變函數性質,使算法性能得以改善。仿真測試結果表明,改進方法具有較好的收斂速度和抗噪聲能力。在實際工程應用中,可將該算法應用于自適應濾波器的設計。1.2 常用的LMS算法
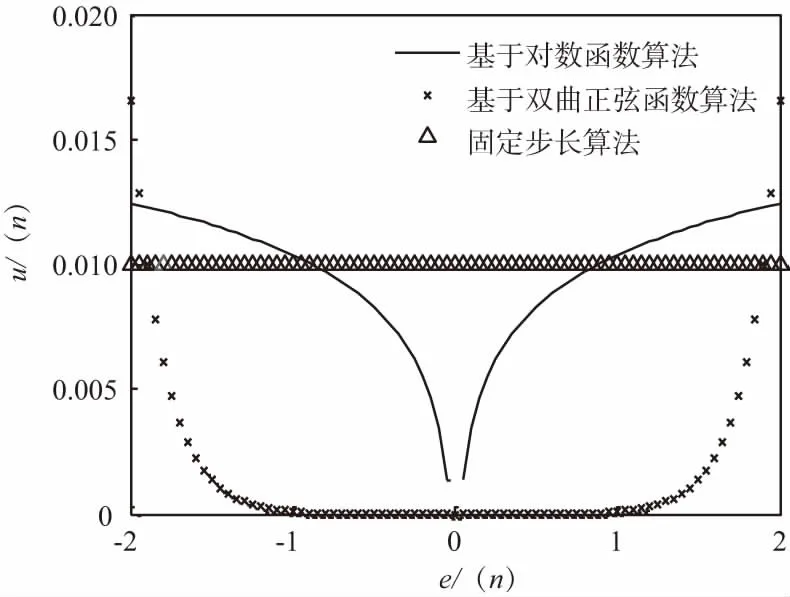
2 基于雙曲正弦函數的新變步長LMS算法
3 算法實現與仿真測試
3.1 實驗仿真環境
3.2 參數的選取
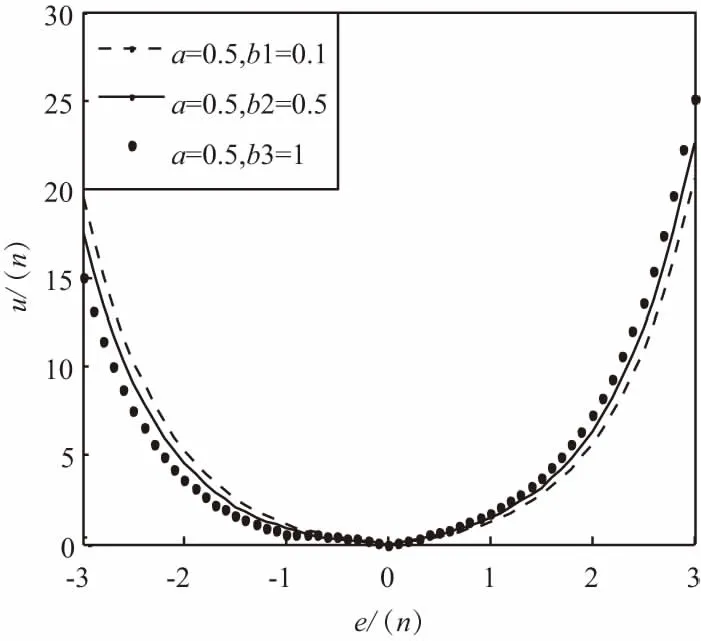
3.3 實驗結果與分析
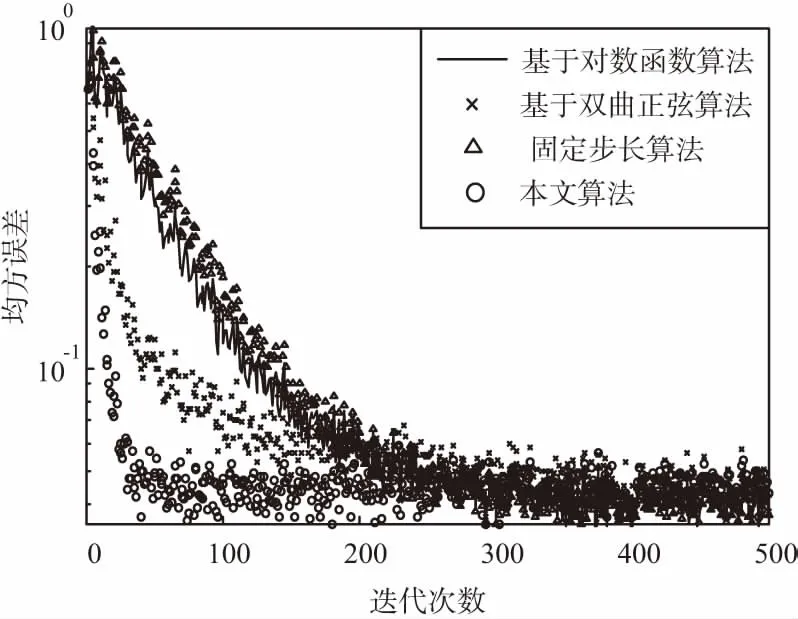
4 結束語

