基于三維Merchant模型的公路改擴建工程路基變形特性研究

陸 軍，宋 亮

（1.新疆維吾爾自治區交通建設管理局，新疆烏魯木齊830049；2.長安大學公路學院，陜西 西安710061；3.新疆維吾爾自治區交通規劃勘察設計研究院，新疆烏魯木齊830006）

0 引言

隨著我國交通量的不斷增加，現有高速公路已無法滿足日益增長的交通需求，越來越多的高速公路存在改擴建的需求，高速公路改擴建項目將是今后我國公路建設的重要任務之一[1?2]。在改擴建項目中，路基拼接設計關系到工程質量和服務水平。然而，新舊路基填料存在彈性模量、黏聚力、內摩擦角等物理力學差異，這些導致了新舊路堤的不均勻沉降以及路面反射裂縫，最終可能導致改擴建項目路基路面的早期損壞[3?5]。

現階段改擴建公路變形研究主要著眼于自重荷載和行車荷載對路基路面的影響，長期以來對自重荷載和車輛荷載引起的路基路面變形研究較多并取得了一定的成果[6?9]。然而這些研究中往往忽略了填筑材料力學性能對新老路基附加變形、沉降差異和路面變形的影響。如Tang等[10]和Dareeju等[11]分別分析了在循環荷載作用下路基整體的變形特性，但是忽略了材料本身特性對變形的影響。Salour等[12]采用RLT試驗分析了粉砂路基的變形規律，但未能很好地分析材料自身性質的影響。Satyal等[13]在進行路堤變形分析時僅考慮了外界環境的影響。王景環等[14]采用Drucker?Prager模型，結合現場沉降觀測資料，分析了路堤填筑材料物理參數對新老路堤附加變形、差異沉降、路堤橫坡變化的影響規律及土工格柵處治交界處路基非均勻沉降機理。陳俊等[15]研究了用于填筑路堤加固的竹筋格柵的力學性能并將其與傳統土工格柵的力學性能進行對比。曹衛平等[16]通過三維土拱效應模型試驗，研究樁—土相對位移、路堤高度、樁帽凈間距和水平加筋體拉伸強度等因素對樁土應力比及路堤沉降的影響。汪益敏等[17]通過室內模型試驗，研究了新舊路基差異沉降作用下土工格柵加筋拓寬路堤填土的工作性狀。汪浩等[18]采用基于二維比奧（Biot）固結理論的平面應變有限元方法分析新路堤作為附加荷載對老路堤和地基的影響。

綜上所述，現有研究未能很好地考慮到填筑材料物理力學性能對拼接路基和擴建路面的影響，尤其是拼接路基工后沉降中的蠕變對公路使用性能的影響，使得分析結果無法全面總結新老路堤不均勻變形規律。針對這些問題，本文采用了三維Mer?chant模型的Prony級數表達式和Drucker?Prager模型表達式模擬填筑材料變形特性，用于模擬拼接路基工后沉降和分析材料變形特性對拼接路基工后沉降的影響規律。

1 有限元模型的建立

1.1 Drucker-Prager模型

Drucker?Prager模型適用于理想彈塑性材料，在道路工程中主要用于模擬半剛性基層與路基[19]。在考慮平均應力影響的情況下，Drucker?Prager模型如公式（1）所示[20]。考慮扁平面Drucker?Prager準則和Mohr?Coulomb準則，采用的外角外接圓表達式如下所示：

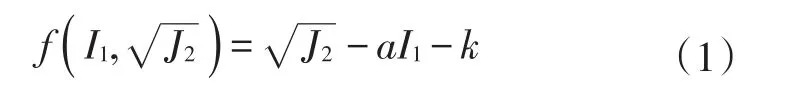
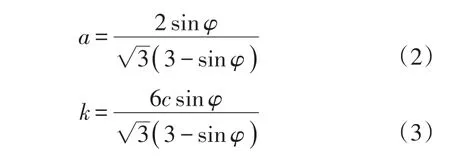
式中：I1為應力張量第一不變量；J2為應力偏張量第二不變量；a和k可由公式（2）和（3）計算得到[21]；c和φ分別為彈塑性填料的黏聚力（kPa）和內摩擦角（°）。由式（1）～式（3）可知，影響Drucker?Prager模型準確性的主要因素是彈塑性填料的黏聚力c和內摩擦角φ。

1.2 三維Merchant模型

在路基及地基的沉降變形中，路堤本身的壓縮變形量占總變形量的比例較小，但是在拼接路基工后沉降中存在一定的蠕變變形仍會影響公路的使用性能，甚至導致反射裂縫等病害，尤其是新疆的砂礫料填筑的路基。上述Drucker?Prager模型可以基本滿足對道路彈塑性填筑材料的模擬，但是無法模擬這類蠕變。因此本文采用Merchant模型模擬工后路基蠕變沉降。一維Merchant基礎模型如圖1所示。

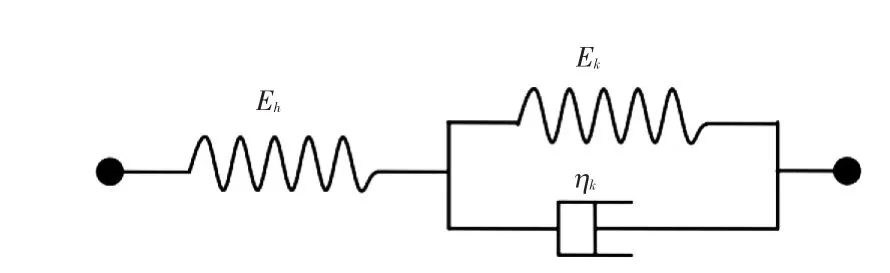
圖1 Merchant模型示意圖

ABAQUS提供的一維Merchant拉壓黏彈性本構方程如下式所示：

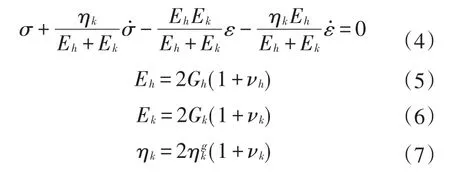
式中：Ek和Eh為一維Merchant拉壓黏彈性模型中與材料彈性模量相關的參數；ηk為材料的黏滯系數；Gk和Gh為與材料剪切松弛模量相關的參數，vk為材料泊松比。則Merchant一維剪切松弛模量和體積松弛模量Prony級數如式（8）、式（9）所示：

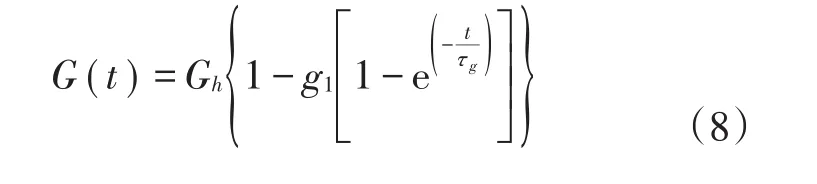
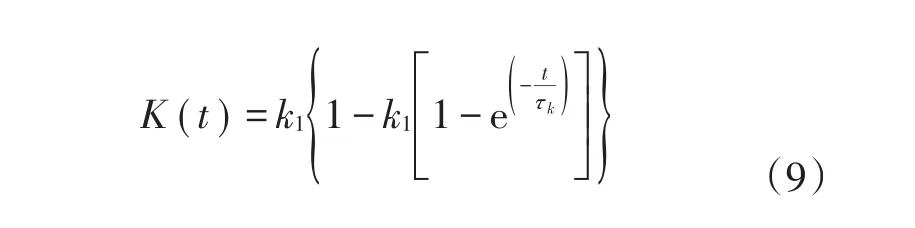
式中：G(t)和K(t)分別為Merchant一維剪切松弛模量Prony級數和體積松弛模量Prony級數；g1,k1分別為與材料剪切松弛模量和體積松弛模量相關的參數；τg和τk分別為材料的抗剪切強度和抗松弛強度。對比式（8）和（9）可知，將上述本構模型推廣至三維必須進行一定的假設。引起拼接路基工后蠕變的主要原因是填料顆粒之間的擠壓和結構重組，這個過程中存在體應變，所以必須考慮體積模量的時間耦合問題。因此本文采用常泊松比假定[22?23]。基于常泊松比假定，Ek=Eh,g1=k1,τk=τg，其中g1,τg計算方式如式（10）、式（11）所示。

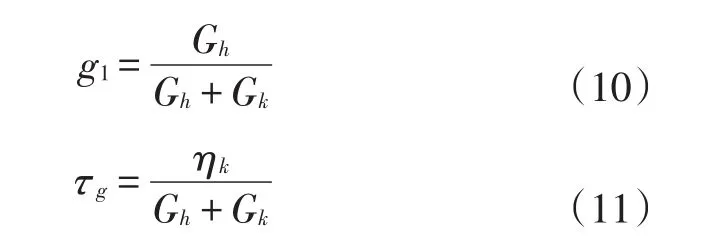
可見，使用基于常泊松比假定的三維Merchant模型僅需要確定泊松比ν,Ek或Eh，黏滯系數ηk即可。

1.3 ABAQUS模型

以連霍高速（G30）新疆境內小草湖—烏魯木齊段改擴建項目標準橫斷面為例，建立三維有限元模型，圖2、圖3分別為標準橫斷面圖和三維有限元模型圖。

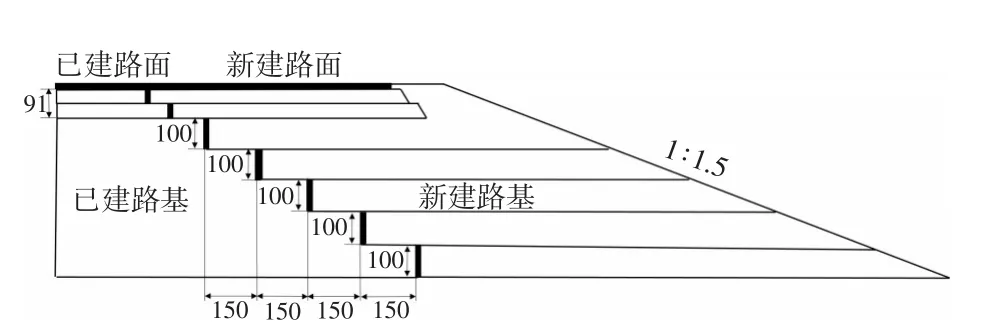
圖2 拼接路基設計圖（單位：cm）

圖3 ABAQUS有限元模型（單位：cm）

模型建立要點如下：

（1）采用三維應力處理，拼接路基部分采用四面體單元；

（2）采用生死單元模擬拼接路堤施工過程；

（3）網格劃分單元邊長為1mm；

（4）鑒于柳浩等[24]研究的瀝青混凝土層間黏結和新舊路基聯結失效機制，本文在層間黏結力和新舊路基聯結處采用黏結?滑移模型模擬；

（5）有限元模型中路面結構采用線彈性材料，路基結構采用Drucker?Prager模型和三維Merchant材料。由上述分析可知，必須確定填筑材料的Eh,Ek,ηk。基于連霍高速（G30）新疆境內小草湖—烏魯木齊段改擴建項目實測數據，本文設定路基長期彈性模量為320MPa，基于高成雷等[25]和劉大鵬等[26]的研究，假設蠕變占路基壓縮變形的45%。其余基本材料參數如表1所示。

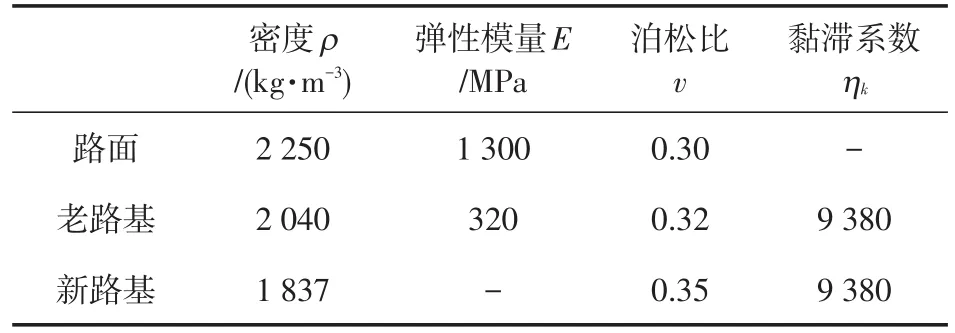
表1 有限元模型材料參數

（6）為確定材料物理性質對拼接路基附加變形、沉降差異和路面變形的影響，選取不同材料參數模擬不同工況，具體參數選取如表2所示。

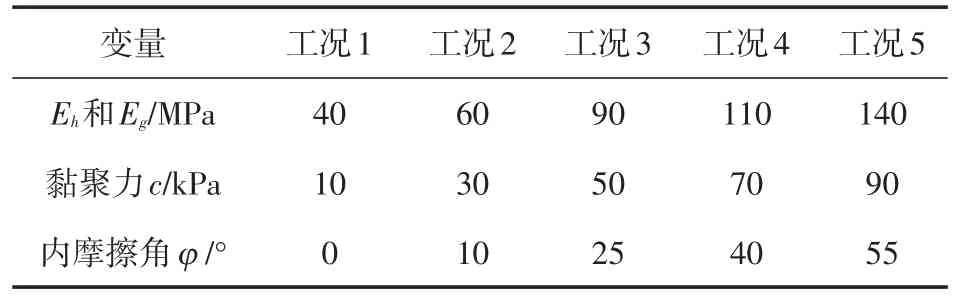
表2 工況參數

（7）上述黏聚力和內摩擦角的范圍（c在10～90kPa之間；φ在0～55°之間）包括了連霍高速（G30）新疆境內小草湖—烏魯木齊段改擴建項目所用路基填土可能出現的所有黏聚力和內摩擦角值。

2 模型計算結果與討論

2.1 彈性模量對路基變形的影響

彈性模量對拼接路基附加變形、沉降差異和路面變形的影響較大。分別采用彈性模量為40MPa,60MPa,90MPa,110MPa,140MPa的新路基填筑材料進行計算，拼接路基表面變形曲線如圖4所示。

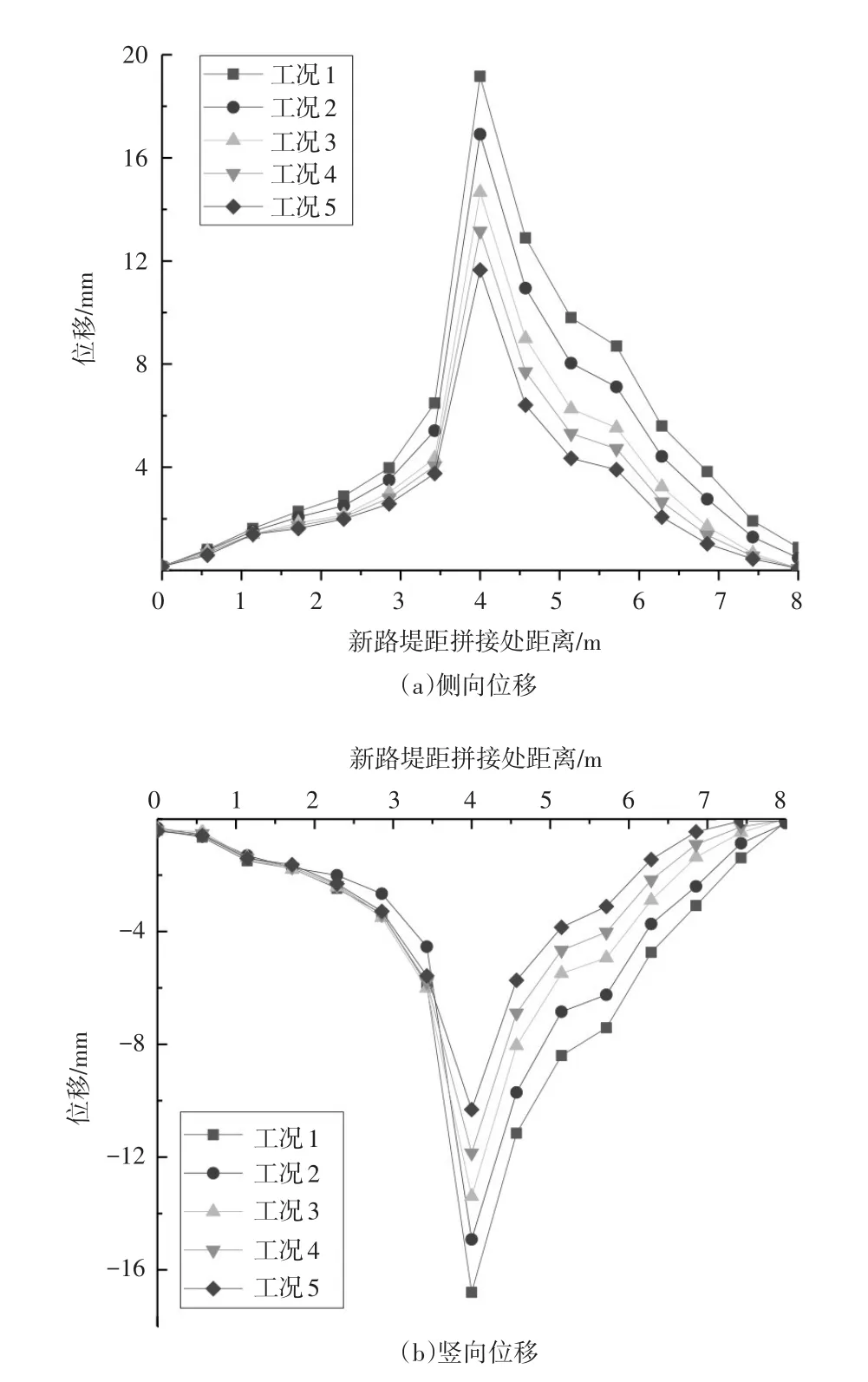
圖4 不同彈性模量路基位移

可見隨著拼接路基彈性模量的增大，路基的附加變形逐步減少，5種工況下最大附加變形分別為25.48mm,22.55mm,19.86mm,17.71mm,15.55mm。5種工況下新舊路基最大沉降差分別為11.80mm,9.92mm,8.39mm,6.85mm,5.31mm。新舊路基的彈性模量差異越小，拼接路基的不均勻沉降也越小。同時，隨著路基附加變形和不均勻沉降的減小，路面變形也呈遞減趨勢。

小草湖—烏魯木齊段改擴建項目路基材料為沿線4處料場的粉砂土，粉砂土的實測彈性模量在80～120MPa之間，在上述分析彈性模量范圍內。試驗段施工分別采用彈性模量為90MPa和110MPa的粉砂土。路基變形檢測結果表明，隨著拼接路基彈性模量的增大，路基變形逐步減少，同時，隨著路基附加變形和不均勻沉降的減小，路面變形也呈遞減趨勢。這些結果表明，試驗段路基變形與有限元模擬結果基本一致。因此，將三維Merchant模型的Prony級數表達式和Drucker?Prager模型表達式運用于有限元模型可以較好地反映拼接路基工后沉降中的蠕變。

2.2 黏聚力對路基變形的影響

黏聚力c是路基填筑材料抗剪強度的重要評價指標，討論c值對拼接路基附加變形和不均勻沉降的影響有助于填筑材料的選定。如表2所示，分別采用黏聚力c為10kPa,30kPa,50kPa,70kPa,90kPa的材料進行計算，結果如圖5所示。

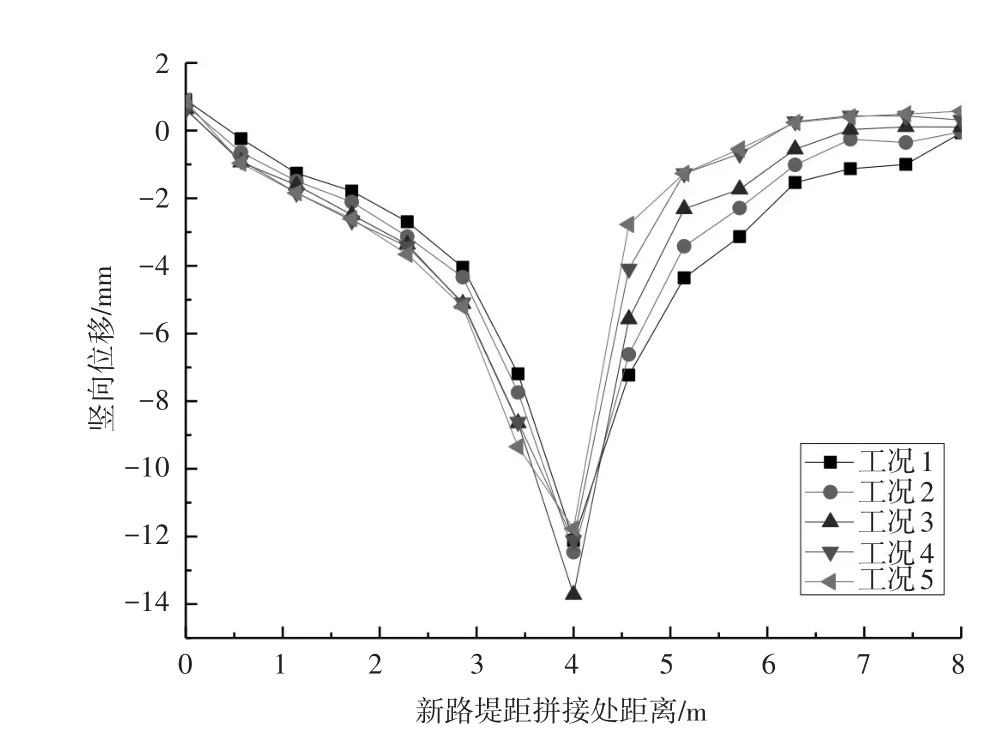
圖5 不同黏聚力路基位移

黏聚力c對側向附加變形的影響很小，主要影響新路基的豎向變形。從新舊路基拼接處至新路基中心，5種工況豎向變形曲線基本重合，因此黏聚力c對此段豎向變形影響較小。從新路基中心至右路肩處，隨著c值減小，路基豎向位移顯著增大。同時5種工況下最大豎向附加變形位于拼接路基中心處，分別為12.116 309 92mm,12.465 565 25mm,13.71718458mm,12.115 918 75mm,11.76677519mm，可見c值對新路基中點處豎向位移影響不大。同時，隨著黏聚力c的增大，路面變形也呈遞減趨勢。

小草湖—烏魯木齊段改擴建項目路基粉砂土的實測黏聚力c在10～30kPa之間。試驗段施工分別采用黏聚力c為10kPa和30kPa的粉砂土。路基變形檢測結果表明從新路基中心至右路肩處，隨著拼接路基黏聚力c的增大，路基側向變形逐步減少。結果表明，試驗段路基變形與有限元模擬結果基本一致。因此，將三維Merchant模型的Prony級數表達式和Drucker?Prager模型表達式運用于有限元模型可以較好地反映拼接路基工后沉降中的蠕變。

2.3 填料內摩擦角對路基變形的影響

內摩擦角φ也是路基抗剪強度的重要評價指標，討論φ值對拼接路基附加變形和不均勻沉降的影響有助于填筑材料的確定。同時對比φ值與c值對路基影響的差異有助于填料選擇。如表2所示，分別采用內摩擦角φ為0°,10°,25°,40°,55°的材料進行計算，計算結果如圖6所示。

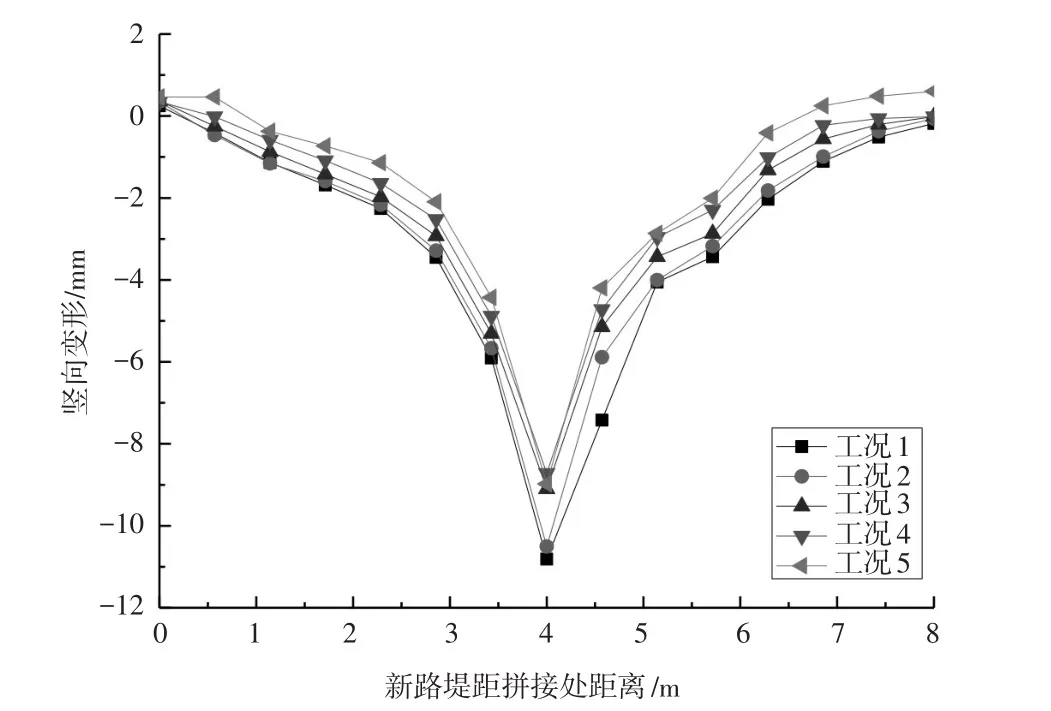
圖6 不同內摩擦角路基位移

在0～55°范圍內，內摩擦角φ對側向附加變形的影響很小，主要影響新路基的豎向變形。隨著內摩擦角的增大，路基的豎向附加變形逐步減少。隨著路基附加變形和拼接路基不均勻沉降的減小，路面變形也呈遞減趨勢。同時內摩擦角φ對新路基中點處豎向位移影響顯著。隨著內摩擦角φ的增大，路面變形也呈遞減趨勢。

對比圖5與圖6，發現黏聚力c對拼接路基豎向變形的影響顯著大于內摩擦角φ值的影響。因此，為減少拼接路基的豎向不均勻沉降和豎向位移應優先保障材料的黏聚力c值滿足工程要求。

小草湖—烏魯木齊段改擴建項目路基粉砂土的內摩擦角φ在25～50°之間，該區間在0～55°范圍內。試驗段施工分別采用內摩擦角φ為25°和40°的粉砂土。路基變形檢測結果表明從新路基中心至右路肩處，隨著拼接路基內摩擦角φ的增大，路基側向變形逐步減少。結果表明，試驗段路基變形與有限元模擬結果基本一致。因此，將三維Merchant模型的Prony級數表達式和Drucker?Prager模型表達式運用于有限元模型可以較好地反映拼接路基工后沉降中的蠕變。

2.4 土工格柵對路基變形的影響

針對國內高速公路拓寬改擴建后部分路段的新舊路基拼接部分相繼發生縱向裂縫的現象，小草湖—烏魯木齊段改擴建項目采用了土工格柵來保證新舊路基銜接穩定。為模擬土工格柵的影響，將筋材和土分開考慮，土與筋材之間設立接觸面單元，將土工格柵設為薄膜單元，作為嵌入區嵌入到路基中去。土工格柵位置與圖2位置相對應。土工格柵容重γ=20.0kN/m3，彈性模量E=19800MPa，其余參數參照工況2。

計算結果表明，當使用土工格柵時工況2下最大附加變形為13.23mm，最大沉降差為8.32mm，最大側向位移為10.19mm；而未使用土工格柵時工況2下最大附加變形為22.55mm，最大沉降差為9.92mm，最大側向位移為20.23mm。可見土工格柵能極大程度地增強路堤的承載力、有效約束土體的側向位移，增強路堤穩固性。

小草湖—烏魯木齊段改擴建項目試驗段路基部分采用了土工格柵，路段新路堤彈性模量為60MPa，黏聚力為30kPa，內摩擦角為10°，與有限元模型參數基本一致。檢測結果表明采用土工格柵的試驗段側向位移和附加變形明顯小于未使用土工格柵的試驗段。因此，將三維Merchant模型的Pro?ny級數表達式和Drucker?Prager模型表達式運用于有限元模型，同時采用薄膜單元模擬土工格柵可以較好地反映使用土工格柵拼接路基工后沉降中的變形。

2.5 工程材料建議

基于上述研究，在連霍高速（G30）新疆境內小草湖—烏魯木齊段改擴建項目設計過程中，沿線設計4處粉砂土，多分布于河漫灘及山前沖積扇上，品質優良，儲量豐富，可開采條件較好，運輸方便。作為路基填料的粉砂土應保證其彈性模量在80MPa以上，黏聚力c控制在10kPa以上或者內摩擦角φ控制在30°以上。同時建議在新老路基彈性模量相差較大的路段使用土工格柵來保證新舊路基銜接穩定。

3 結論

（1）新舊路基填筑材料彈性模量差距越大，工后拼接路基的附加變形和不均勻沉降也越大。同時隨著路基附加變形和拼接路基不均勻沉降的增大，路面變形也呈遞增趨勢。

（2）黏聚力c對側向附加變形的影響很小，主要影響新路基的豎向變形。拼接路基豎向位移和不均勻沉降隨著黏聚力c的減小，先減小后增大。當c在10～90kPa的范圍內時，黏聚力主要影響范圍是新路基中心至右路肩處。

（3）在0～55°范圍內，內摩擦角φ對側向附加變形的影響很小，主要影響新路基的豎向變形。隨著內摩擦角的增大，路基的豎向附加變形逐步減少。內摩擦角φ值對拼接路基豎向變形的影響顯著小于黏聚力c的影響。

（4）將三維Merchant模型的Prony級數表達式和Drucker?Prager模型表達式運用于有限元模型，同時采用薄膜單元模擬土工格柵可以較好地反映使用土工格柵的拼接路基工后沉降中的變形。土工格柵能極大程度地增強路堤的承載力、有效約束土體的側向位移，增強路堤穩固性能，有利于減少新舊路基拼接部分的縱向裂縫。