基于反饋線性化的兩輪自平衡汽車側傾動態響應控制

熊宇聰，張 猛,2

（1.北京控制工程研究所，北京 100089；2.北京軒宇空間科技有限公司，北京 100089）

0 引言

隨著智能交通工具研究的興起，具有側傾控制的兩輪自平衡汽車憑借其外形輕巧、駕駛靈活等優點受到了國內外的廣泛關注[1]。兩輪汽車的動力學模型是典型的非線性欠驅動非完整約束系統[2]，在無相對滑動的理想情況下，兩輪汽車的前后輪的橫向和縱向運動均受到由地面形成的非完整約束，且兩輪汽車在側傾方向無直接驅動激勵，因此在極低速行駛或靜止的情況下，無法保持車身的平衡[3]。目前，針對兩輪汽車模型欠驅動的特點，相關研究人員提出了多種控制機構以維持兩輪汽車的自平衡，包括方向轉向[4]，重量平衡體[5]和控制力矩陀螺儀（CMG）[6]三種控制機構。相較而言，控制力矩陀螺儀具有輸出力矩大、易于使用電氣控制等優點[6]，因此獲得了廣泛研究。通過控制力矩陀螺儀提供側傾方向力矩，控制兩輪汽車在側傾方向獲得期望的姿態響應是兩輪自平衡汽車的關鍵技術之一。

文獻[6]利用Euler-Lagrange方法推導了基于單個控制力矩陀螺儀兩輪汽車的動力學模型，給出了一種基于模型的雙環自抗擾控制方法（Active Disturbance Rejection Control），這種控制方法主要采用兩個串聯擴展狀態觀測器和兩個具有自抗擾作用的狀態反饋控制律，實現了兩輪汽車的在側傾角為2°范圍內恢復平衡和對側傾方向姿態干擾的抑制。文獻[7]利用Euler-Lagrange方法推導了與文獻[6]相似的兩輪汽車動力學模型，并對得到的非線性模型在平衡點處進行了線性化，設計了狀態反饋控制方法，使兩輪自平衡汽車可從側傾角為3°左右恢復平衡。文獻[8]采用了與文獻[6]相同的動力學模型，并設計了滑模變結構控制器，實驗表明，該控制方法能使兩輪汽車在側傾角度為26°時恢復到直立平衡狀態。文獻[9]采用了文獻[7]相似的兩輪汽車動力學模型，在平衡點附近進行線性化，并提出了模糊滑模控制和自適應模糊滑模控制兩種控制方法。實驗表明，兩種控制方法均能維持兩輪汽車在平衡點附近的平衡狀態，比較兩種控制方法，自適應模糊滑模控制方法具有更強的抑制干擾能力。

對于兩輪自平衡汽車側傾方向的動力學模型為非線性動力學模型，上述文獻均采用了平衡點處線性化處理方法，不可避免的存在線性化誤差。此外，對于姿態控制，兩輪自平衡汽車的動態響應和穩態響應是兩個主要關注因素，而上述文獻主要關注兩輪自平衡汽車側傾方向姿態控制的穩態響應，未開展動態響應過程分析。

本文綜合研究了兩輪自平衡汽車側傾動態響應控制問題，采用反饋線性化方法將兩輪自平衡汽車的非線性動力學模型轉換為線性動力學模型，避免了兩輪自平衡汽車動力學系統在平衡點附近的線性化處理，從而消除了線性化誤差的影響。利用狀態反饋對轉換的線性動力學模型進行極點配置，設計兩輪自平衡汽車側傾方向的動態響應過程，建立兩輪自平衡汽車側傾方向動態響應指標與反饋系數之間的函數關系，在保證兩輪自平衡汽車控制系統具有良好的穩態響應的同時，兼顧控制系統的動態響應。針對所設計的動態響應過程，采用PI控制器實現控制力矩陀螺儀的力矩輸出調節，實現所設計的動態響應過程，滿足相應的動態響應指標要求。最后，本文結合具體的仿真算例驗證了所提出的基于反饋線性化控制方法的有效性。

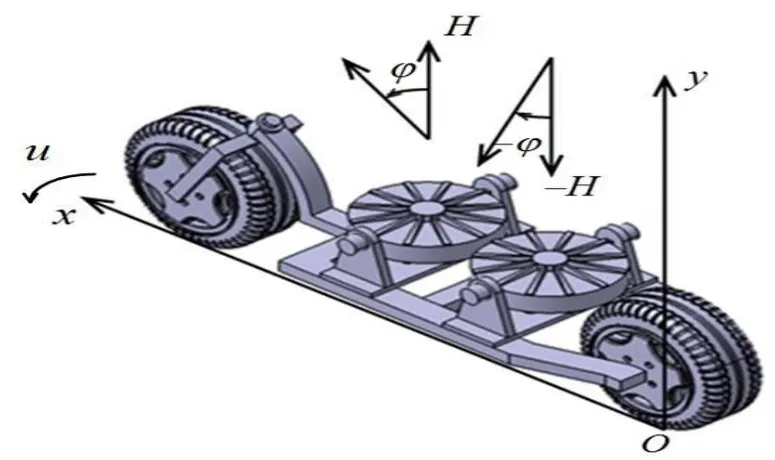
圖1 兩輪汽車底部機械結構圖

圖2 控制系統結構圖

1 兩輪自平衡車模型

1.1 系統結構

本節介紹兩輪自平衡汽車機械結構和控制系統結構。圖1給出了兩輪自平衡汽車底部機械結構圖。如圖1所示，兩輪自平衡汽車底部安裝一組控制力矩陀螺儀對兩輪汽車進行側傾姿態控制，一組控制力矩陀螺儀反向旋轉，在驅動電機作用下反向旋進，以產生側傾方向的控制力矩。

圖2給出了兩輪自平衡汽車控制系統結構圖。如圖2所示，控制系統由測量單元、控制單元和執行單元三部分構成，三個部分通過車輛供電母線供電并通過車輛通信總線實現通信，控制單元包括自平衡控制器和CMG控制器，測量單元包括陀螺儀和加速度計，執行單元包括CMG和CMG驅動器。

1.2 動力學模型

圖3給出了兩輪自平衡汽車車體受力示意圖。如圖3(a)所示，兩輪自平衡汽車保持直立狀態時，O點與O'點分別為前后輪與地面之間的接觸點，以后輪與地面接觸點O為坐標原點，Ox軸與水平方向OO'軸重合，Oy軸沿鉛垂方向，Oz軸根據右手法則確定，指：向紙面外。h為兩輪自平衡汽車質心高度。如圖3(b)所示，兩輪自平衡汽車車體繞側傾軸Ox軸發生側傾運動時，側傾角為地面對兩輪汽車的彈力與摩擦力的作用線通過側傾軸Ox，力矩為0，車體質量為m時，車體受到重力矩mghsin與控制力矩陀螺儀產生的控制力矩u的合力矩作用，矢量正方向為圖示方向。由動力學原理，兩輪自平衡汽車側傾運動的動力學方程為：

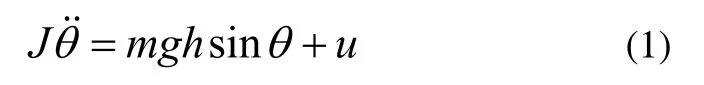
其中，J為兩輪自平衡汽車整車相對側傾軸Ox軸的轉動慣量。

圖3 兩輪自平衡汽車受力圖

兩輪自平衡汽車自平衡系統由一組控制力矩陀螺儀和一組旋進電機組成，如圖1所示。圖4給出了控制力矩陀螺儀輸出力矩圖，當兩輪汽車側傾角度為時，控制力矩陀螺儀角動量所在的平面為Oxy'平面，兩個控制力矩陀螺儀在驅動電機作用下反向旋進，旋進角的模為?，旋進角速度的模為。單個控制力矩陀螺儀角動量H大小不變，旋進角度為?時，其在側傾軸Ox軸和Oy'上的投影分別為：

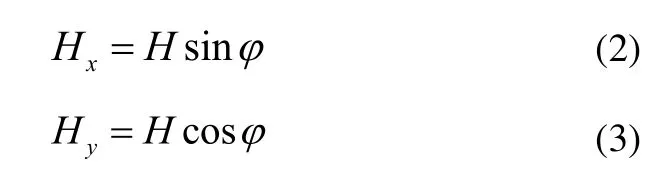
式(2)和式(3)求導得：

圖4所示控制力矩陀螺儀之間具有對偶關系，因此控制力矩陀螺儀在旋進過程中角動量的總變化量為方向沿Ox正方向。根據角動量守恒，車體所受控制力矩u沿Ox軸負方向，大小為：

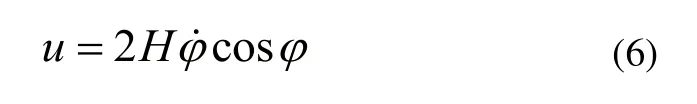
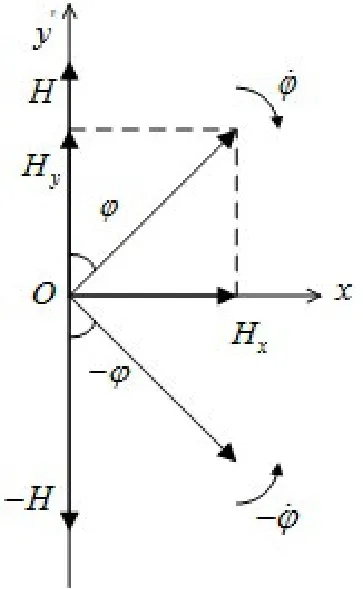
圖4 控制力矩陀螺儀輸出

2 控制系統設計

2.1 車體控制

根據式(1)，兩輪自平衡汽車車體的動力學模型為非線性二階系統。為了精確控制非線性二階系統的動態響應，構造參考力矩輸入uref，當控制力矩陀螺儀產生的實際輸入u滿足：

兩輪自平衡汽車側傾方向的動態響應滿足期望動態響應指標要求。式(7)成立時，根據兩輪自平衡汽車車體的動力學模型(1)，式(8)成立：

式(8)所對應的系統框圖如圖5(a)所示。

非線性二階系統動態響應形式復雜，而在兩輪自平衡汽車控制系統中，狀態變量側傾角度與側傾角速度可以通過測量元件實時測量，在車體質量m，車體質心高度h已知的情況下，采用反饋線性化控制，在參考力矩uref中引入靜態反饋作用量其控制系統框圖如圖5(b)所示，即：

其中，u1為參考力矩的線性作用部分。

式(9)代入式(8)得：

式(10)對應系統框圖如圖5(c)所示，通過在參考力矩uref中引入靜態反饋作用量車體二階非線性系統轉換為二階線性系統。利用狀態變量側傾角度與側傾角速度可實現二階線性系統動態響應的精確控制。設計狀態反饋如圖5(d)所示。

圖5 車體控制設計

即：

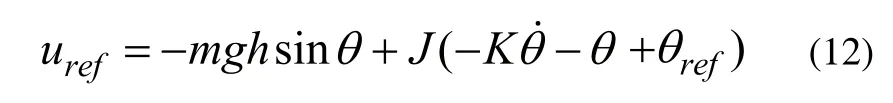
式(11)代入式(10)可得：

拉普拉斯變換得：

對于兩輪自平衡汽車從初始側傾角度恢復至直立狀態，動態響應過程為階躍響應[7]。

由于階躍響應與單位階躍響應相差常數倍，研究單位階躍響應可以得到階躍響應的全部性質，由式(14)，根據二階線性系統理論當K=0時，兩輪自平衡汽車的階躍動態響應為無阻尼響應，響應過程為：

當0＜K＜2時，兩輪自平衡汽車的階躍動態響應為欠阻尼響應，響應過程的動態響應指標與速度反饋系數K之間的函數關系如下：

延遲時間td：

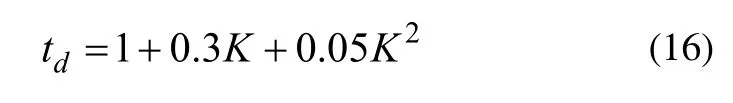
上升時間tr：

峰值時間tp：

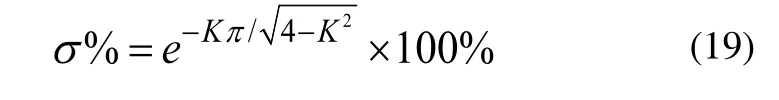
調節時間ts：

當K=2時，兩輪自平衡汽車的階躍動態響應為臨界阻尼響應，響應過程為：

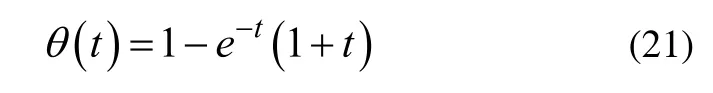
當K＞2時，兩輪自平衡汽車的階躍動態響應為過阻尼響應，響應過程的動態響應指標與K之間的函數關系為：

延遲時間td：

上升時間tr：

式(15)～式(23)建立了動態響應過程指標與速度反饋系數K之間的函數關系，通過調整K值可以使兩輪自平衡汽車側傾動態響應滿足期望的動態響應指標。

2.2 控制力矩陀螺儀控制

為實現2.1節所設計的車體側傾動態過程，控制力矩陀螺儀的輸出力矩為：

根據CMG的輸出力矩模型(6)，參考力矩uref所對應的陀螺儀旋進角度ref與旋進角速度ref滿足：

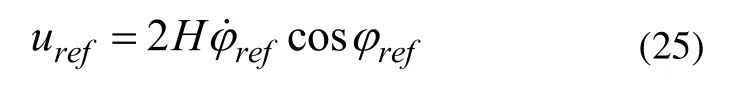
對比式(6)與式(25)，當控制力矩陀螺儀的旋進角度與旋進角速度滿足式(26)時，式(24)成立。

控制力矩陀螺儀的旋進角速度由驅動電機控制，對于驅動電機，其調速控制式(26)可由單位負反饋結合PI控制器實現，如圖6所示。

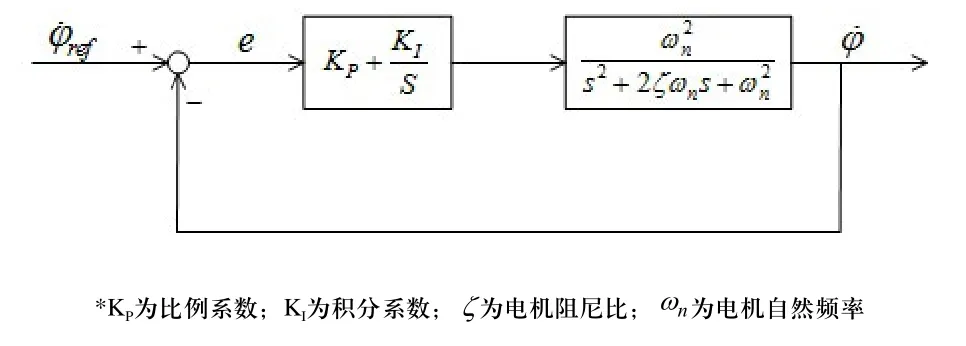
圖6 驅動電機控制

2.3 穩定性證明

兩輪自平衡汽車控制系統由兩部分構成，分別為車體自平衡控制系統和控制力矩陀螺儀控制系統，控制系統工作原理如圖7所示。由姿態測量單元測量兩輪自平衡汽車當前側

對于控制力矩陀螺儀控制系統，輸入輸出穩定的充要條件為圖6所示閉環控制系統特征方程的根位于復平面的左半平面。

圖6所示閉環控制系統的特征方程為：

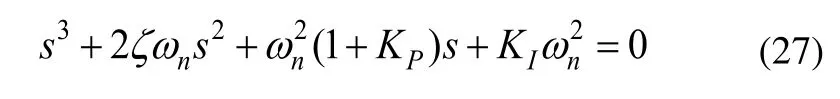
根據勞斯-赫爾維茲穩定性判據，式(27)的根位于復平面左半平面的充要條件是：

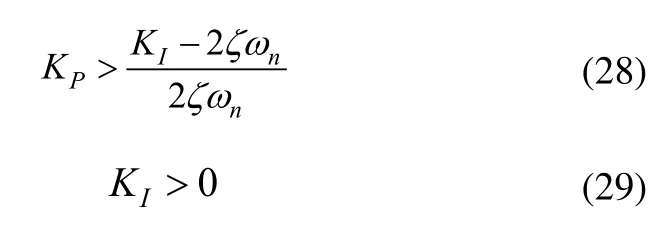
式(28)與式(29)成立時，控制力矩陀螺儀輸入輸出穩定。圖6所示控制系統誤差函數為：

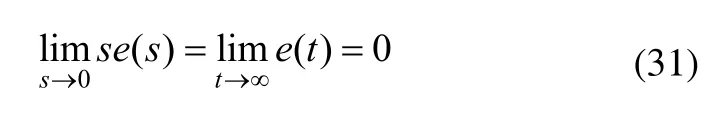
此時，式(26)和式(24)成立，從而兩輪自平衡汽車側傾方向動態響應為(14)，其特征方程為：

式(30)的根位于復平面左半平面的充要條件為：

當式(28)、式(29)、式(31)與式(33)同時成立時，控制系統輸入輸出穩定。

3 控制系統仿真

3.1 性能驗證仿真參數

某車型兩輪自平衡汽車相關物理參數如表1所示。

表1 兩輪自平衡汽車相關參數

兩輪自平衡汽車側傾方向的姿態響應過程為階躍響應。對于所設計的控制系統，兩輪自平衡汽車能維持平衡的充要條件為式(24)成立。對于式(24)，具有如下性質：在任意非平衡位置處，控制力矩陀螺儀的輸出力矩u的模大于車體所受重力矩mghsin的模，且兩者方向保持相反。由表1參數計算可知，兩輪自平衡汽車所受重力矩最大為490N.m。由于控制力矩陀螺儀隨著驅動電機的旋進，輸出力矩單調遞減，為了滿足兩輪自平衡汽車保持平衡的充要條件，設置初始側傾角度為15°，約0.26rad，控制力矩陀螺儀的最大輸出為800N.m，參考側傾角度為0°，即平衡位置。

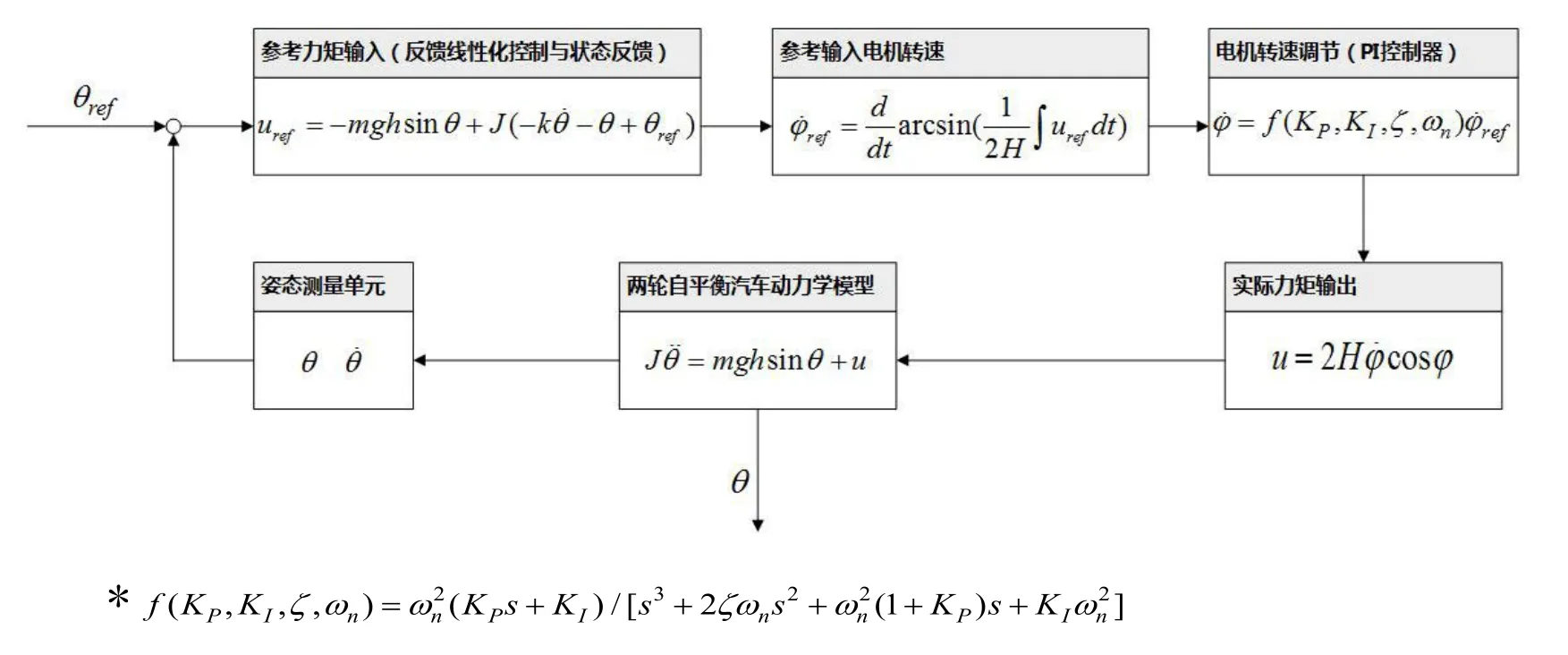
圖7 控制系統工作原理圖

對于上述仿真條件，控制力矩陀螺儀控制器參數可選取KP=8，KI=2，自平衡控制器參數分別選取K=0（無阻尼），K=1（欠阻尼），K=2（臨界阻尼），K=3（過阻尼）四種仿真參數分別驗證式(15)～式(23)。

在MATLAB/SIMULINK軟件中，選擇Runge-Kutt積分方法，以1ms為定步長對本文提出的側傾姿態控制方法進行性能仿真驗證。

3.2 性能驗證仿真結果

分別選取K=0（無阻尼），K=1（欠阻尼），K=2（臨界阻尼），K=3（過阻尼）四種仿真參數對兩輪自平衡汽車側傾方向動態響應進行驗證，仿真結果如圖8所示。

圖8 性能驗證結果

從圖8(a)可以看出，當K=0時，兩輪自平衡汽車在控制器作用下在平衡位置附近做等幅振蕩運動，振幅為15°，振蕩周期為T=6.28s，符合式(15)計算得到的動態響應。在圖8(b)中，兩輪自平衡汽車車體側傾動態響應為欠阻尼響應，根據(16)式～式(20)計算，延遲時間td=1.35s，最大峰值時間tp與上升時間tr為3.62s，超調量為σ%=16.32%，與仿真實驗結果一致。從圖8(c)與圖8(d)可以得出，當K=2和K=3＞2時，兩輪自平衡汽車側傾方向動態響應為臨界阻尼響應和過阻尼響應，根據式(21)～式(23)式計算，延遲時間td分別為1.8s和2.35s，上升時間分別為3.5s和5.5s，與實驗結果一致。由上述實驗結果可知，通過改變自平衡控制器的速度反饋系數K值，可以定量調整兩輪自平衡汽車車體側傾方向響應的動態指標，動態響應指標與K值之間的函數關系式為式(15)～式(21)。

3.3 動態響應設計與仿真

為說明本文提出的控制器對兩輪自平衡汽車側傾動態響應的控制能力，針對側傾動態響應的動態響應指標約束，計算符合約束要求的速度反饋系數K值，進一步仿真驗證。

在初始側傾角度為30°時，回復至平衡狀態的動態響應指標要求如下：

解上述不等式組(35)，可得速度反饋系數滿足0.714≤K≤0.88，選取K=0.8，進行仿真驗證，結果如圖9所示。將K=0.8代入式(16)～式(20)計算可得td=1.272s，tr=2.16s，tp=3.426s，σ%=25%滿足動態響應指標約束。

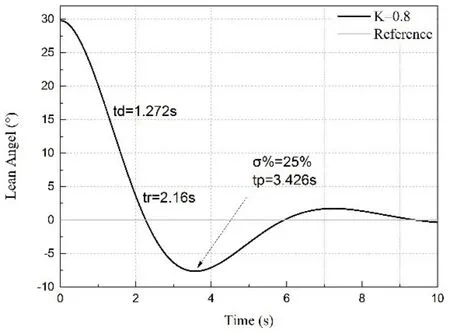
圖9 動態響應設計結果

4 結論

對于有駕駛人員參與駕駛的兩輪自平衡汽車，車體側傾方向姿態控制系統的動態響應和穩態響應是兩輪自平衡汽車側傾姿態控制的兩個重要因素。本文提出了基于反饋線性化的控制綜合控制方法，利用反饋線性化將兩輪自平衡汽車的非線性動力學模型轉換成為線性動力學模型，消除了在平衡點處線性化引起的線性化誤差。針對線性動力學模型設計了狀態反饋，并建立速度反饋系數K與動態響應指標之間的函數關系，通過改變速度反饋系數K，可準確改變兩輪自平衡汽車側傾方向動態響應指標，定量設計動態響應過程。針對所設計的動態響應過程，本文為提供側傾力矩的控制力矩陀螺儀輸出力矩調節設計了PI控制器，并證明了整車控制系統的輸入輸出穩定性，為兩輪自平衡汽車側傾方向姿態控制提供了一種新的控制算法。最后通過具體車型的仿真結果說明了本文提出的控制算法的有效性。