出藥機構動力學仿真及優化分析

（北京信息科技大學 機電工程學院，北京 100192）

0 引言

當前在我國醫院藥房取藥過程中，患者常常排隊等藥，發錯藥的事故也時有發生。傳統的醫院儲藥系統主要由普通的藥架構成，藥品的存儲密度低，藥品的發送基本上是由醫務人員根據處方人工配送，這種模式的發藥速度慢，效率低。實現藥房自動化不僅可以幫助醫院提高發藥的速度更能增加發藥的準確度。采用機械手式的自動存取設備出藥不僅速度慢、控制電路繁瑣、且可靠性差。為解決上述問題，本研究提供了一種出藥快捷，工作可靠的出藥機構[1～4]。

1 出藥機構原理

出藥系統主要包括平行排列的斜坡儲藥槽和出藥機構。出藥機構主要由電磁鐵線圈、電磁鐵鐵芯、出藥機構底座、連桿、搖桿、擋藥滾輪、導向滾輪；擋藥滾輪設置在斜坡儲藥槽前方，送藥時對藥盒起導向作用，導向滾輪鉸接于搖桿前端。如圖1所示。

出藥單元與水平方向成25°角放置，在電磁鐵線圈不通電的狀態下，搖桿與出藥機構底座的方向平行，擋藥滾輪擋住藥盒，將其擋在儲藥槽上；在電磁鐵線圈通電的狀態下，電磁鐵的鐵芯與線圈吸合，拉動連桿繼而拉動搖桿向上傾斜，把藥盒頂高，當藥盒前端底部高于擋藥滾輪時，藥盒借助重力經由導向滾輪導向滑出。當電磁鐵的拉回動作結束后，電磁鐵鐵芯在彈簧的復位作用下回到初始位置。

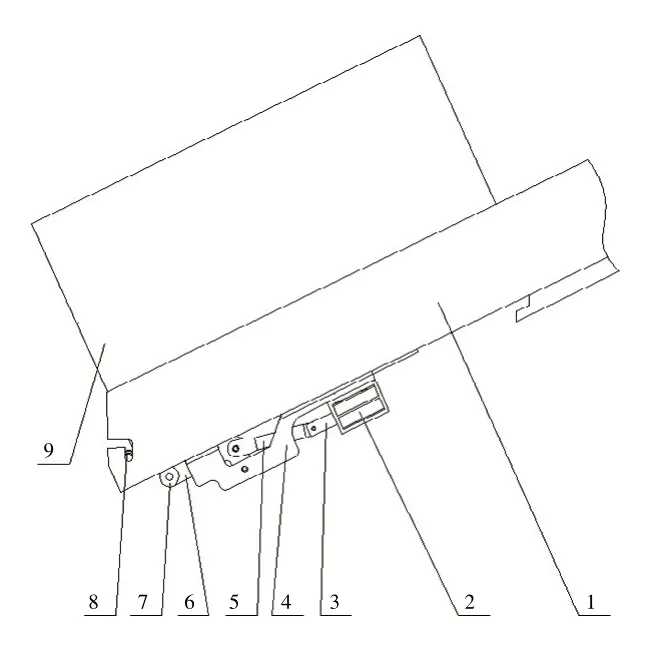
圖1 出藥機構結構示意圖

這種出藥機構結構簡單，快速準確，且可靠性高。實現了大型藥房藥品的自動發放，節約了人力成本，提高了工作效率。

2 出藥機構受力分析

如圖2所示，將出藥機構簡化為一搖桿—滑塊機構，進行受力分析。藥盒在彈射過程中，電磁鐵提供拉力FM，搖桿前端受藥盒阻力F。

采用復數矢量法對該機構進行受力分析，以A點為原點建立直角坐標系，并將各構件的桿矢量及方位角示出。將各運動副中的反力統一表示為FRij的形式，即構件i作用于構件j上的反力，且規定i＞j，二構件j作用于構件i上的反力FRji則用-FRij表示。再將各運動副中的反力分解為沿兩坐標軸的兩個分力示出。

圖2 桿件受力分析簡圖

選取運動副B為首解副，并取構件1為分離體，并將諸力對A點取矩，則根據得：

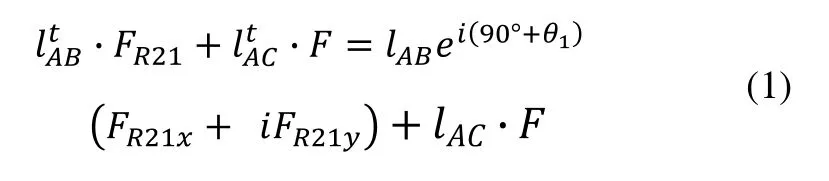
由上式的實部等于零可得：

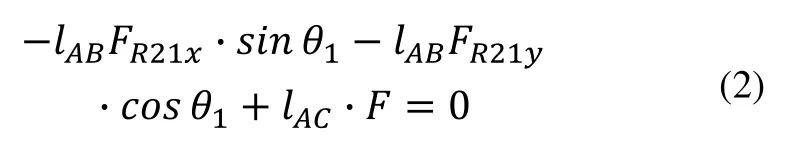
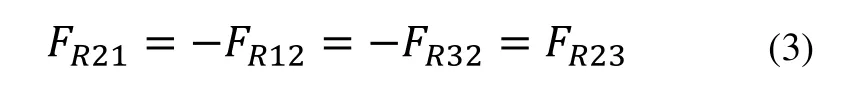
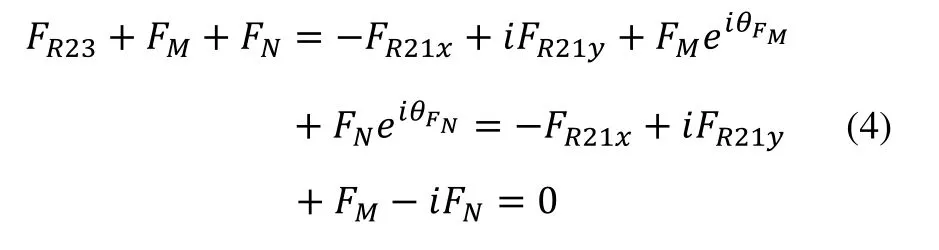
由上式的實部和虛部分別等于零可得：

將上式帶入式(1)，得：

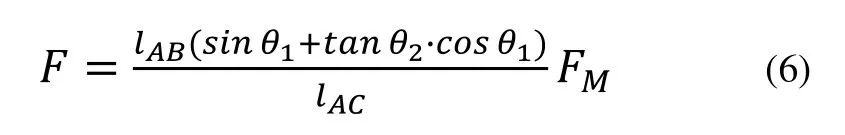
又由FN=FM.tan(180°-θ2)=-FMtanθ2，上式可化為：

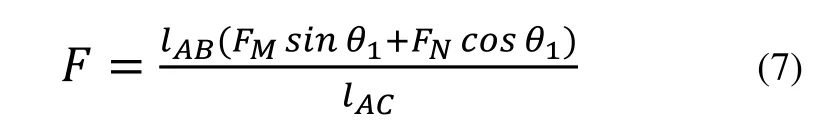
3 藥盒動力學分析及仿真

3.1 藥盒動力學分析

出藥機構上藥時，藥盒重力在平行于藥槽方向的分力應大于藥盒和藥槽之間的靜摩擦力，即：

式中fs為藥盒與藥槽間的摩擦系數，此處取值為0.13。

出藥機構進行出藥動作時，藥盒在搖桿的作用力下脫離藥槽做平面運動，包括質心的拋物運動和繞質心的轉動。根據力的平移定理和合力矩定理，將藥盒所受的力系簡化，并將藥盒作為剛體處理。簡化后的藥盒受力情況如圖3所示。

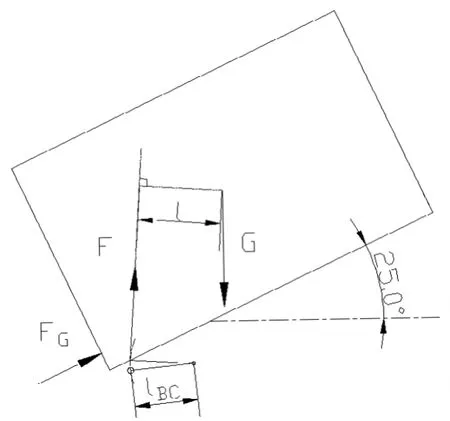
圖3 藥盒受力分析模

在藥盒被搖桿頂起時，藥盒在豎直方向受重力G，平行于藥槽方向受到擋藥滾輪的支持力FN，以及在與搖桿接觸點處受到搖桿的作用力F。在如圖3所示瞬間，剛體平面運動微分方程在自然直角坐標軸上的投影式為：

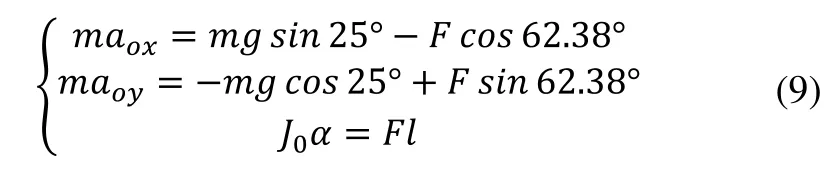
解得藥盒被頂起瞬間質心加速度與角加速度：

式中l為力F對O點的力臂，l=55.46mm；J0為藥盒對重心O的轉動慣量，其中a、b分別為藥盒的長度和寬度。

3.2 基于ADAMS的藥盒動力學仿真分析

3.2.1 虛擬樣機模型的建立

由于虛擬樣機技術在進行運動學、動力學求解時，只考慮零件的質心和質量，而對零件的外部形狀不予考慮。因此，要對出藥機構的形態結構進行適當的簡化[5]：

1）各鉸接處以轉動副來約束，等效實現二者的相對運動；

2）各部件為剛體；

3）忽略轉動副摩擦。

根據出藥機構實際形態結構，按照以上原則，建立了虛擬樣機模型，如圖4所示。

圖4 出藥機構虛擬樣機模型

根據電磁鐵吸力特性，分別對通電率為50%與25%時兩種情況進行仿真，電磁鐵吸力特性曲線如圖5所示。

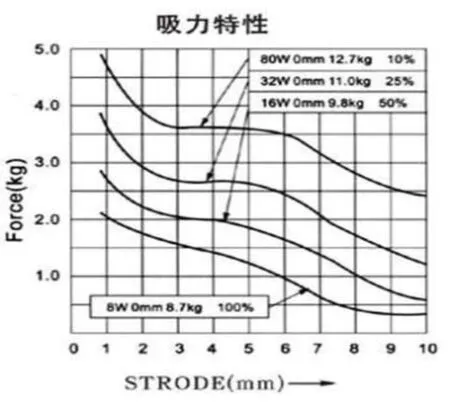
圖5 電磁鐵吸力特性曲線

3.2.2 仿真分析

仿真結果如圖6所示，其中圖6(a)和圖6(b)分別為通電率為50%和25%時出藥機構仿真結果。

如圖6(a)、圖6(b)所示，左上圖為藥盒彈射過程，其中黑色曲線為藥盒質心的運動軌跡。右上圖為藥盒的角加速度曲線，左下圖為藥盒質心在水平方向的速度曲線，右下圖為藥盒質心在豎直方向的速度曲線。可見藥盒在彈出后的運動包含拋物運動及繞其質心的旋轉運動，因此需根據藥盒的運動軌跡合理選取彈出點與輸送裝置的高度差和水平距離等參數，防止藥盒掉落時脫離輸送裝置或發生傾覆。

4 出藥機構優化分析

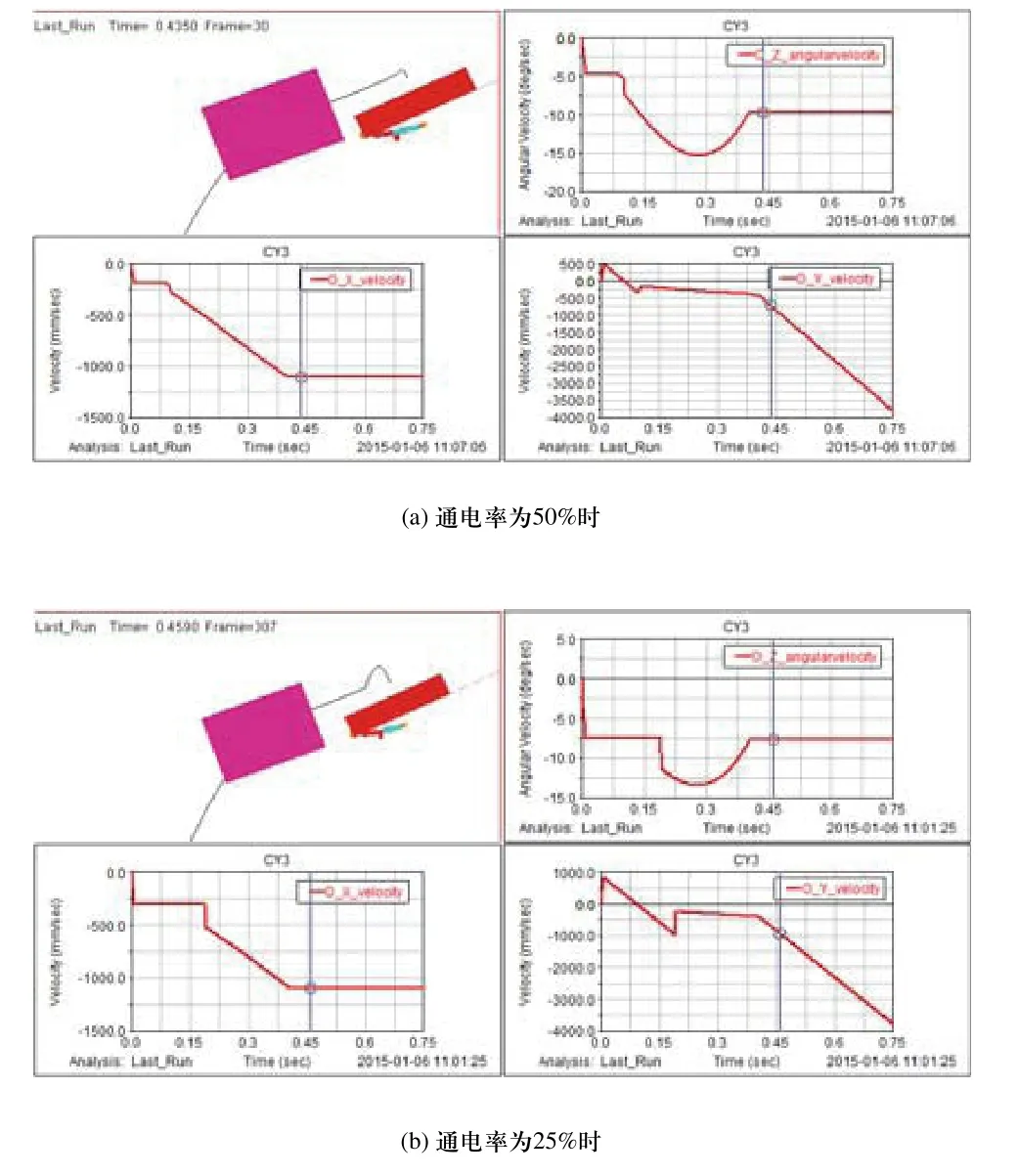
圖6 出藥機構仿真結果

由于儲存在藥槽中的藥盒質量不同，被彈射出來的運動軌跡也不一樣，質量小的彈射距離高，質量大的彈射距離低。且當出藥機構的輸出力不合理時會使藥盒無法被彈起或超出合理彈起高度。因此需基于藥盒初速度最大化對出藥機構各桿件參數進行優化設計，使不同種類的藥品在空中的運動軌跡最優化[6]。

由于搖桿-滑塊機構由LAB、LBC、LBD等參數確定，式(6)表明搖桿作用力與LAB、LBC有關，因此取設計變量為：

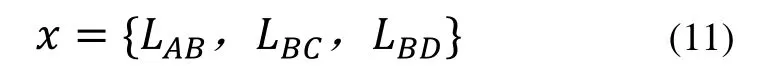
以藥盒質心垂直于藥槽的初速度最大為尋優目標函數，以確定最優桿長方案，取目標函數為：

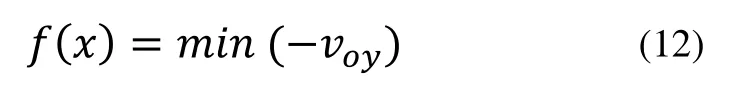
約束條件的建立首先應滿足構成偏心搖桿-滑塊機構的桿長條件，即LAB+e≥L_BD，其中e為偏距，其值為3.5。同時受于空間位置約束，LAB與LBC不能太長。

確定設計變量、目標函數和約束條件后，采用ADAMS對虛擬樣機進行參數化建模，采用設計研究模塊使各設計變量在一定范圍內進行取值，根據設計變量值的不同進行一系列仿真分析并輸出各次仿真分析的結果，找出哪些設計變量對目標函數的靈敏度最高。

靈敏度表征目標函數對設計變量值的變化的敏感程度。靈敏度分析是優化設計的鋪墊工作，用來確定重要的設計參數，通過預訂參數定量分析每個設計參數對目標函數影響的程度，從而縮小研究范圍，在優化設計時做重點考慮[7,8]。靈敏度大小以前后兩次試驗靈敏度的平均值表示[9]：

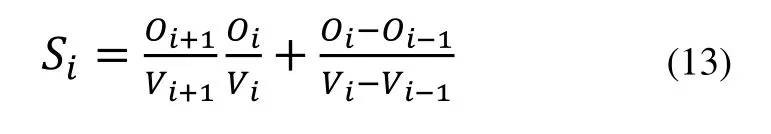
上式中：O為目標值，V為設計參數值，i為迭代次數。

LAB、LBC、LBD各自變化對目標函數的影響曲線分別如圖7～圖9所示。

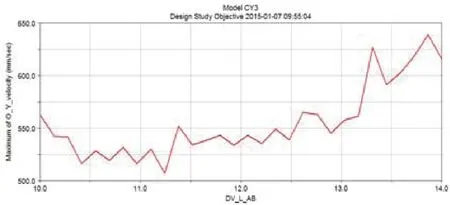
圖7 LAB變化對目標函數的影響曲線

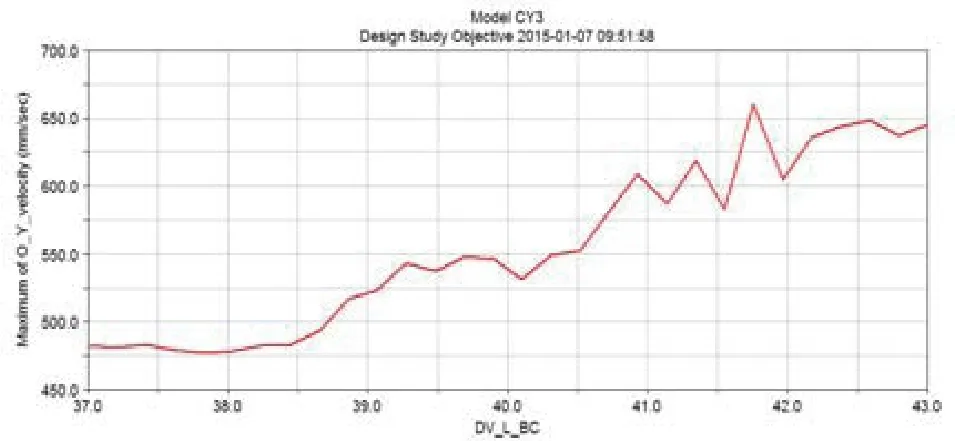
圖8 LBC變化對目標函數的影響曲線

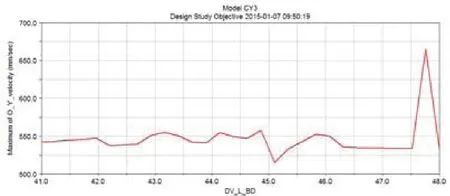
圖9 LBD變化對目標函數的影響曲線

其中LAB取值為13.172時靈敏度值最大，為249.01；LBC取值為40.724時靈敏度值最大，為136.12；LBD取值為47.517時靈敏度值最大，為271.74。

通過試驗設計模塊對多個設計變量的取值組成組，研究在設計變量取不同的可能組合時目標函數的取值情況，進行優化求解。求解過程中各次迭代的曲線變化如圖10所示，其中橫坐標為迭代步，縱坐標為藥盒質心垂直于藥槽的初速度值。

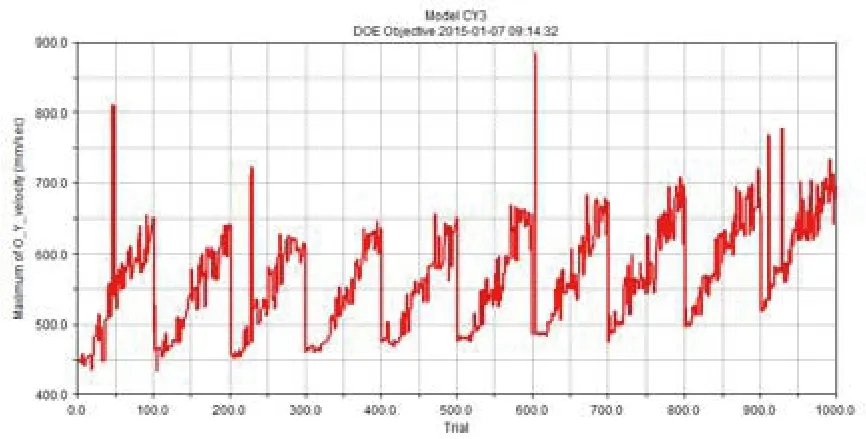
圖10 優化迭代曲線

最優解為第604迭代步，其設計變量取值為：

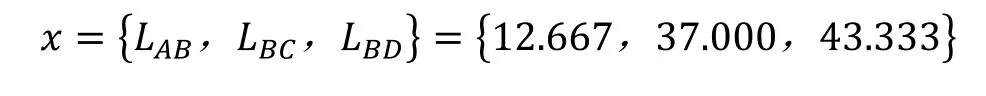
由優化結果可看出，優化后藥盒質心垂直于藥槽的初速度voy=885.13。

5 結論

闡述了出藥機構的原理及動作過程，對出藥機構和藥盒進行了受力分析。建立了出藥機構的虛擬樣機模型，并對其進行了基于ADAMS的動力學分析，得出了在不同電磁鐵通電率下的藥盒質心軌跡曲線。對出藥機構進行了優化設計，并對各設計變量進行了靈敏度分析，得到了藥盒質心垂直于藥槽的初速度最大時出藥機構的各桿長最優解。綜上，本研究為機構設計提供了實用方法，為出藥機構最終的尺寸設計提供了依據，為藥房自動化系統設計奠定了理論基礎。