“探索圖形”教學紀實、反思與評析
韓巍 王巖
教學目標:
1.加深對正方體特征的認識和理解。
2.通過觀察、列表、想象等方式探索、發現圖形分類計數問題中的規律,體會化繁為簡解決問題的策略。
3.培養空間想象力,體會分類、數形結合、歸納、推理、模型等數學思想。
教學重點:學會從簡單的情況找規律,解決復雜問題的化繁為簡的思想方法。
教學難點:探索規律的歸納方法。
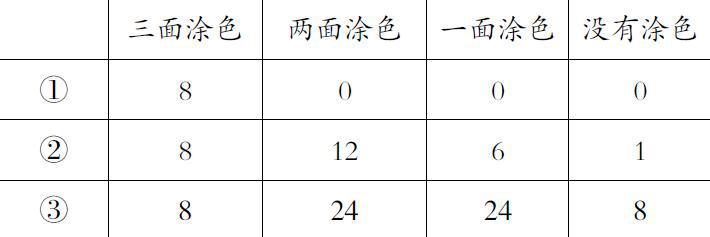
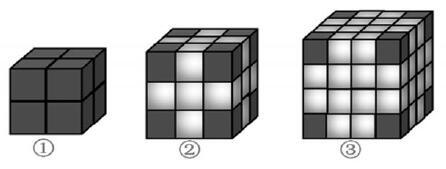
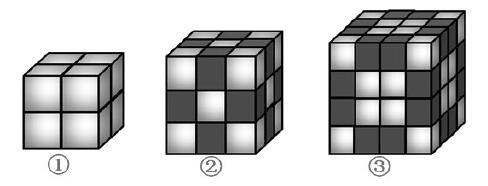
教具準備:2、3、4階魔方,學習單,課件。
教學過程:
一、 巧設障礙,引發思考
師:請大家看,黑板上出現的是什么圖形?
生:正方體。
師:正方體有哪些特點呢?
生:正方體有8個頂點,12條棱和6個面。
師:同學們,如果我對這個大正方體進行切割,請看這就是切割后的圖形,你們知道現在它是由多少個小正方體組成的嗎?
生:這個大正方體是由729個小正方體組成的。
師:這個數據你是怎么得到的呢?
生:我發現這個大正方體長寬高都被平均分成了9份,利用求正方體的體積公式我就求出了它有729個小正方體。
師:你可真了不起,通過細致的觀察,利用以前學過的知識就得到了準確的答案。
師:現在我們把這個大的組合圖形的表面涂漆,你知道什么是表面涂漆嗎?
生:就是把這個大正方體的外面圖上漆。
師:里面涂嗎?
生:里面不涂。
師:請大家猜測一下,每個小正方體的涂漆會如何呢?
生:有三面涂漆、兩面涂漆、一面涂漆還有沒涂上漆的。
師:為什么還有沒涂上漆的呢?
生:被包在里面的就涂不上。
師:還有其他情況嗎?
生:沒有。
師:每一類小正方體分別有多少個呢?我們來分類填一填。(出示表格)如果請你來數一數,你有什么感覺?
生:太多了,數不過來啊!
師:看來這個圖形太復雜了,數起來很麻煩,你有什么好辦法解決這個問題嗎?
生:我算一算。
師:你一定是有了什么方法,你是怎么得到這樣的方法的呢?
生:我們化繁為簡,可以研究比較簡單的正方體,看看有什么規律,然后再解決這個問題。
師:下面,我們就來用這個辦法嘗試一下。
二、 合作探究,完成建模
(一) 嘗試解決,發現規律
師:你認為什么樣的圖形比較簡單,容易找到答案呢?
生:長寬高各有2個正方體,3個正方體,4個正方體的圖形。
出示合作要求
兩人一組合作研究。活動要求:
1.借助手中的魔方,數一數、算一算,把結果填在記錄表中。
2.觀察表中記錄的數據,看看你發現了什么。
(生四人為一組合作研究。)
師:說說你的發現。
生:三面涂色的小正方體都位于大正方體的頂點的位置,都有8個。
生:三階魔方中,兩面涂色的是位于每條棱的中間,每條棱上有一個小正方體,12條棱就有12個小正方體。
師:你是怎么算出來的呢?
生:如果一條棱上有3個正方體,減去兩邊的正方體,就是1,再用1乘12得到12個小正方體。
師:那么四階魔方呢?
生:一條棱上有4個正方體,減去兩邊的正方體,就是2,再用2乘12得到24個小正方體。
師:還有其他發現嗎?
生:一面涂色的是每個面上除去外圈的小正方體。
師:你是怎么算出每個面上除去外圈的小正方體的個數呢?
生:以3階魔方為例,一個面有9個小正方形,外圈有8個,9-8=1,面上就有1個。
師:這位同學是用一個面的總個數減去外圈的數量得到的數據。還有什么方法嗎?
生:以3階魔方為例,一個面橫著看有3行小正方體,減去上下兩行就是中間1行,就有1個小正方體一面涂色。
師:那么,你列的算式就是3-2=1,是嗎?如果用這樣的思路來解決4階魔方可以嗎?
生:不行,4-2=2,可是我們數出的是一個面有4個小正方體一面涂色啊!
生:以4階魔方為例,一個面橫著看有4行小正方體,減去上下兩行就是中間2行,豎著看有4列小正方體,減去左右兩列就是中間2列,2乘2就是4個小正方體一面涂色。
師:你真是一個善于觀察、善于總結方法的學生,就一面涂色的情況誰還有自己的發現?
生:我發現一個面的正方形個數就可以用求面積的方法,長是2,寬是2,2乘2就得4了,再用4乘6個面就得到了24。
師:你把求平面圖形面積的方法用在了求一面涂色的塊數上,真有辦法。
生:我還發現用小正方體的總數量減去前三項的數量就是中間沒有涂色的數量。
師:你很善于思考,還有其他方法得到沒有涂色的數量嗎?
生:我發現4階魔方的里面沒有涂色的就是2階魔方,3階魔方的里面就是1個小正方體。
生:以3階魔方為例,我發現如果用3減2就得到1了。
生:我認為這種方法不對,如果是4階魔方也不能用4減2啊。
師:是啊,那么怎么來數、來算呢?
生:4階魔方有4層小正方體,去掉上下2層就剩下中間2層了,前后數共4行去掉前后2行剩下中間2行,左右數共4列去掉左右2列剩下中間2列,所以是2乘2乘2得到的8個。
師:老師這里有個非常直觀的課件,誰愿意像他描述的這樣來操作一下?
(生一邊操作一邊講解。)
師:看來這個中心部分的塊數、我們可以借助求正方體的體積的方法得到。
師:大家看這兩種算中間沒有涂漆的小正方體的結果一樣嗎?
生:一樣。
師:雖然我們看不到里面的中心部分,但是我們用這兩種方法都可以解決這個問題,而且它們相互驗證了結果的準確性。
(二) 應用規律,解決問題
師:大家有了這么多發現和方法,現在你們能解決稍微復雜的問題了嗎?我們來試一試吧!以小組為單位算一算5×5×5、6×6×6的正方體,并繼續完成表格。
匯報交流:
生:用n表示正方體的棱長(所含小正方體的塊數),規律可以這樣表示:三面涂色小正方體的塊數=8(頂點的個數),兩面涂色小正方體的塊數=(n-2)×12,一面涂色小正方體的塊數=(n-2)2×6,沒有涂色小正方體的塊數=(n-2)3。
師:你真善于總結,你在這幾個公式中有什么發現嗎?
生:我發現除了三面涂色是與8個頂點位置的正方體有關,其他的分別是(n-2)的一次方,(n-2)的二次方,(n-2)的三次方。
師:為什么有這樣的規律呢?
生:因為求兩面涂色的正方體在棱上,棱上中間有幾個正方體再乘12條棱,一面涂色的正方體是在面上,要用中間長和寬相乘,而長和寬又相同,所以就是平方數乘6個面,最里面沒有涂色的部分實際是個正方體,所以是立方數。
師:你善于觀察和總結,把這幾種涂色情況分析得真透徹。
師:現在我們再來解決課開始前的問題吧!
三、 結合實際,引發興趣
師:在生活中,這種利用規律解決問題的情況還有很多,如金字塔圖形的數量問題,正方體組成長方體涂漆問題,都可以利用我們今天學到化繁為簡的方法來分析解決,還有把數學知識運用到其他領域的情況,如工程設計、美術裝飾,希望同學們都能有善于發現善于總結的學習習慣,去解開更多的秘密。
反思:
“數學好玩”是我校正在探索實踐的課程,它以數學學科為載體,廣泛挖掘課內外學習資源,充分調動學生學習積極主動性,以培養學生數學核心素養為目標。在我執教的“探索圖形”一課時,從設計到實施,也努力以此為依據。
首先,我設計了兩次以小組為單位的交流實踐活動,通過第一次觀察、想象和推理數一數、算一算每種涂色情況,并嘗試用列表的方法表示出來,逐步發現每種涂色情況的位置和規律。在此基礎上,學生進行第二次活動,應用規律解決問題,在數學實踐活動中學會合作、學會交流,享受成功的喜悅,體驗數學學習的樂趣。
第二,我將數學思想融入到此次學習中,從數學問題的提出到引導學生利用化繁為簡的數學思想解決問題,從數一數、算一算、填一填的學習活動到發現分類計數問題中的規律,從歸納、推理的研究交流到建立數形結合、完成建模的學習體驗,一步一步引導學生把握問題共性的同時發展學生的空間觀念及空間想象能力。
第三,在本節課中我力求深度挖掘教材,以小學階段接觸到的空間幾何領域的點、線、面、體的知識體系串聯本課學習內容,并與一次方、二次方、三次方的代數知識對接,讓學生感受到數學學習的連貫性和遞進性,體會數學領域的神奇以及學習數學的樂趣。
評析:
1.“數學好玩”讓學生“玩”起來
“數學好玩”課程的顯著特點之一就是讓學生真正成為學習的主體,利用合作、交流以及探究等多種形式“玩”起來。本節課教師就舍得將課堂時間留給學生,第一次探究的時間為8分鐘,第二次合作交流的時間為5分鐘,在一節40分鐘的課中,這13分鐘的時間是不短的,同時課堂上采用小組活動和全員參與活動相結合的形式,讓學生有了充分的活動時間和空間,提供了發現總結規律的機會,在活動中品嘗到了成功的樂趣。
2.“數學好玩”體現核心素養
“數學好玩”這一課程以提升數學核心素養為中心,培養學生數學抽象、邏輯推理、數學建模、數學運算、直觀想象、數據分析的能力。本課教學中,教師就現有的教材進行了深入的鉆研,帶領學生感悟到化繁為簡的數學思想,經歷建立數學模型的過程,從分類計數、推理和數形結合體驗中,豐富了思維活動經驗,尤其是在課程接近尾聲的時候,自然地揭示了三面涂色、兩面涂色、一面涂色、沒有涂色和點、線、面、體的關系,感知了從一維空間、二維空間到三維空間的數學模型建立體系。讓學生經歷將實際問題抽象成數學模型并運用的過程。
3.“數學好玩”從知識本位走向課程本位
“數學好玩”作為花園小學研發的一項課程,不是以知識為唯一或幾乎以知識為唯一的教學目標,而是致力于凸顯學生在課程學習中發生的變化,思維由淺入深逐步提升,學習興趣逐漸濃厚,自信心顯著提升,追求從知識本位走向課程本位。這節課中,教師關注的是如何讓學生愛上數學,利用喜歡的魔方作為學具,拉近生活、游戲與學習的距離,暢談“你的發現”培養學生習慣用數學的思維分析并解決問題,共同合作交流促進情感態度價值觀的建立。
編輯/魏繼軍

