構(gòu)架式可展開天線自由度與奇異性分析

，，*，，，

1. 中國空間技術(shù)研究院 西安分院，西安 710100 2. 燕山大學(xué) 機械工程學(xué)院，秦皇島 066004

構(gòu)架式可展開天線是一種由多基本單元組合而成的大型桁架結(jié)構(gòu)，具有收納比高、精度高、結(jié)構(gòu)穩(wěn)定性好等特點[1]。構(gòu)架式天線按基本單元形狀分為平面構(gòu)架天線和空間構(gòu)架天線，如三角形平面單元[2]和四面體單元[3-4]、四棱錐單元[5]、六棱臺單元[6]等。根據(jù)基本單元的尺寸大小和單元間連接形式可構(gòu)造不同桁架結(jié)構(gòu)系統(tǒng)，滿足不同天線反射面的設(shè)計要求。目前已有多個大型的構(gòu)架式可展開天線成功應(yīng)用于俄羅斯“自然號”、“聯(lián)盟號”飛船、“資源”系列衛(wèi)星及“和平號”空間站等多個航天任務(wù)中。大部分天線都是針對四面體為基本組成單元進行研制，如General Dynamics Corporation(GDC)研制的5.2m構(gòu)架式天線[7]，Johnson Space Center(JSC)研制出的口徑7m的構(gòu)架式可展天線并成功應(yīng)用在“Kondor”航天器上[8]。

四面體單元構(gòu)架可展開天線表現(xiàn)出多環(huán)耦合、模塊化、大尺度柔性等特征，啟發(fā)了關(guān)于構(gòu)架可展開天線在構(gòu)型結(jié)構(gòu)設(shè)計、力學(xué)分析等領(lǐng)域的研究與深入發(fā)展。文獻[9]對構(gòu)架幾何進行了分析，特別是對各鉸鏈進行了設(shè)計，滿足多桿在花盤位置的運動。文獻[10]描述了構(gòu)架式天線四面體單元在節(jié)點處有3根腹桿和6根同步桿，腹桿和同步桿節(jié)點處有滑塊驅(qū)動并同步運動，彈簧提供驅(qū)動力，驅(qū)動位置設(shè)有阻尼器。文獻[11]基于拉格朗日等式，考慮了空間構(gòu)架式反射器展開數(shù)學(xué)模型，估計反射器中桿件的載荷受力。由于數(shù)學(xué)模型對運動特征考慮不全面，嘗試建立起展開物理模型，在尺寸分析和物理狀態(tài)等前提下，以獲得相同參數(shù)為基礎(chǔ)，可識別出描述天線展開的主要參數(shù)。文獻[12]介紹了天線反射器的結(jié)構(gòu)總體方案和關(guān)鍵部件的結(jié)構(gòu)設(shè)計，同時對反射器的形面精度、熱變形及剛度等指標進行了分析計算，驗證了此四面體可展開天線可以滿足衛(wèi)星對天線的系統(tǒng)指標要求。文獻[13]對SAR衛(wèi)星構(gòu)架可展開天線進行了模態(tài)分析，為驅(qū)動的參數(shù)提供了設(shè)計依據(jù)。文獻[14]闡述了四面體單元構(gòu)架式天線總體、結(jié)構(gòu)和電氣方面的研究設(shè)計，并從力學(xué)和熱變形角度進行了實際工況分析。

上述文獻對構(gòu)架式可展開天線的整體結(jié)構(gòu)及剛體動力學(xué)進行了詳細的分析，但對天線機構(gòu)構(gòu)型綜合研究較少。且四面體單元構(gòu)架式天線桿件及花盤等構(gòu)件眾多，導(dǎo)致天線展開時運動協(xié)調(diào)性得不到保證。為保證天線展開時各部件協(xié)調(diào)動作，避免出現(xiàn)展開不完全的現(xiàn)象，需對天線基本單元在展開過程中的自由度和奇異性進行分析，構(gòu)建花盤姿態(tài)運動的特點，對提高大型可展天線這一典型關(guān)鍵載荷產(chǎn)品的可靠性，開展大型可展天線構(gòu)型的研究具有重要的理論基礎(chǔ)和工程價值。

1 構(gòu)架式天線構(gòu)型分析

構(gòu)架式天線屬于大型空間可展機構(gòu)，由若干四面體單元構(gòu)成，如圖1所示。在連續(xù)展開過程中，其四面體單元屬于變胞機構(gòu)，其特點為自由度和拓撲結(jié)構(gòu)可變且能根據(jù)不同工作任務(wù)改變約束特征，但構(gòu)型綜合難度較大。根據(jù)變胞機構(gòu)的這些特點使得對構(gòu)架式天線的結(jié)構(gòu)分析和設(shè)計中存在一定的困難。四面體變胞單元為多環(huán)機構(gòu)，且具有高度耦合性，為保證航天機構(gòu)工作可靠性，通常桿件以轉(zhuǎn)動副R連接。以構(gòu)型為3RR-3RRR的四面體單元為研究對象，構(gòu)件與構(gòu)件之間連接方式由轉(zhuǎn)動鉸鏈相連，如圖2所示。構(gòu)架式天線零部件多，運動較為復(fù)雜，并且現(xiàn)有的四面體單元構(gòu)架式天線在展開到工作位置時具有很大的瞬時沖擊。為分析構(gòu)架式天線各部件運動的協(xié)調(diào)性，可根據(jù)螺旋理論能同時表示運動副軸線的位置和運動副類型的特點[15-16]，采用螺旋理論對構(gòu)架式天線進行自由度研究，分析四面體單元的奇異性及組網(wǎng)后的運動學(xué)特性，保證構(gòu)架式天線展開協(xié)調(diào)。

圖1 四面體單元構(gòu)架式天線Fig.1 A truss antenna composed by tetrahedral elements

圖2 3RR-3RRR單元及花盤結(jié)構(gòu)Fig.2 3RR-3RRR element and disk structure

四面體單元的閉環(huán)數(shù)為[17]：

l=g-n+1=15-13+1=3

(1)

式中：l為獨立閉環(huán)數(shù)目；g為運動副數(shù)目；n為桿件數(shù)目。

為計算簡便，將具有3個閉環(huán)數(shù)的四面體單元拆分為二閉環(huán)機構(gòu)和兩桿件機構(gòu)，如圖3所示。2閉環(huán)機構(gòu)的兩點A、C的運動確定時，兩桿件上相對應(yīng)的兩端點運動也確定[18]。因此，在分析二閉環(huán)機構(gòu)的基礎(chǔ)上可知3RR-3RRR單元的運動特性。

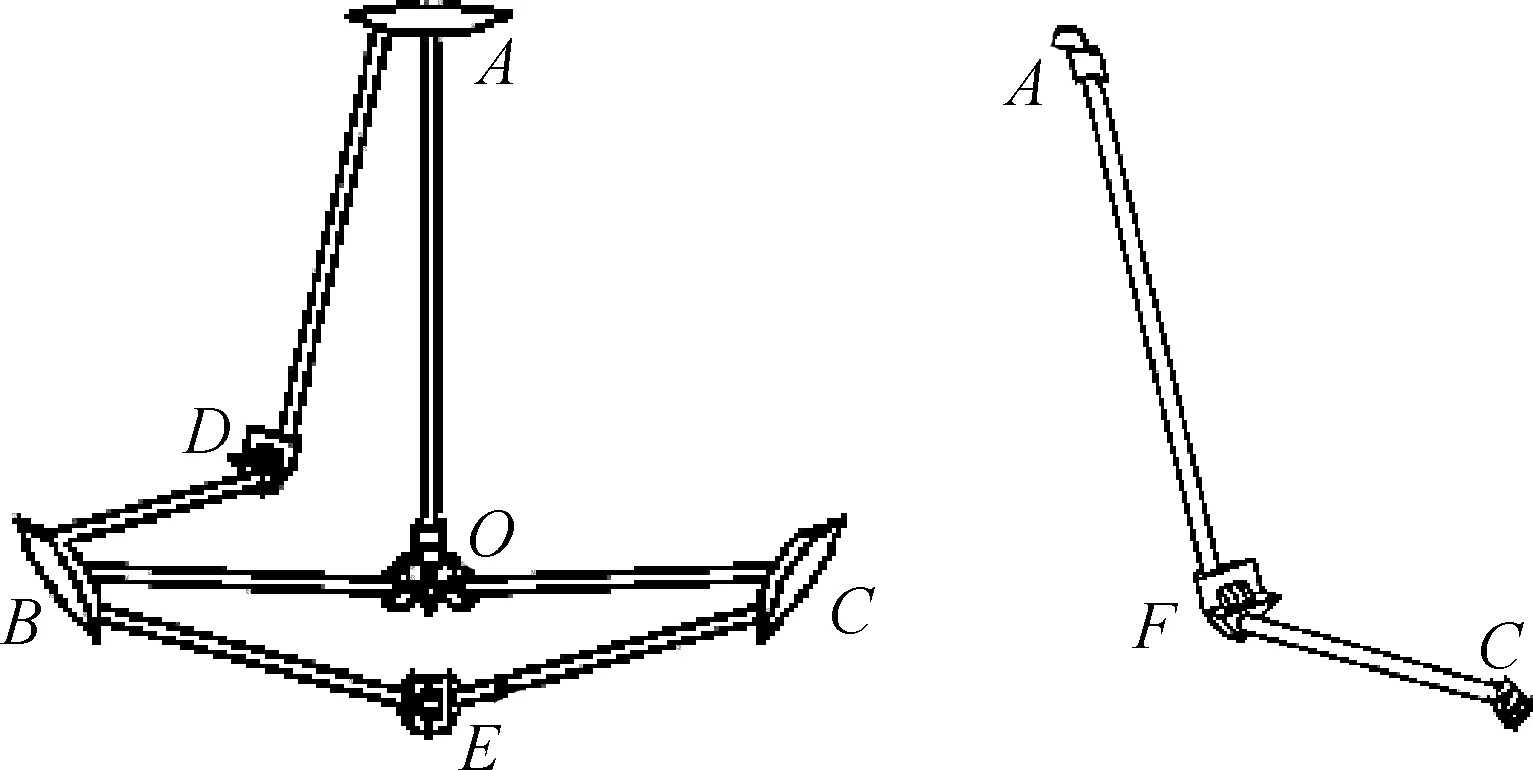
圖3 四面體單元拆分Fig.3 Decomposition of the tetrahedron

2 構(gòu)架式天線單元自由度分析

2.1 單閉環(huán)機構(gòu)的自由度

對3RR-3RRR機構(gòu)最基本的認識是自由度及其奇異特性，但由于過約束的存在，使自由度計算成為一個難點。首先考慮獨立的單閉環(huán)機構(gòu)的自由度，如圖4所示。花盤O在平面ABC上的投影為原點P，原點P到直線AB的垂線為x軸，平面ABC的法線方向為z軸，以右手定則確立y軸建立坐標系。

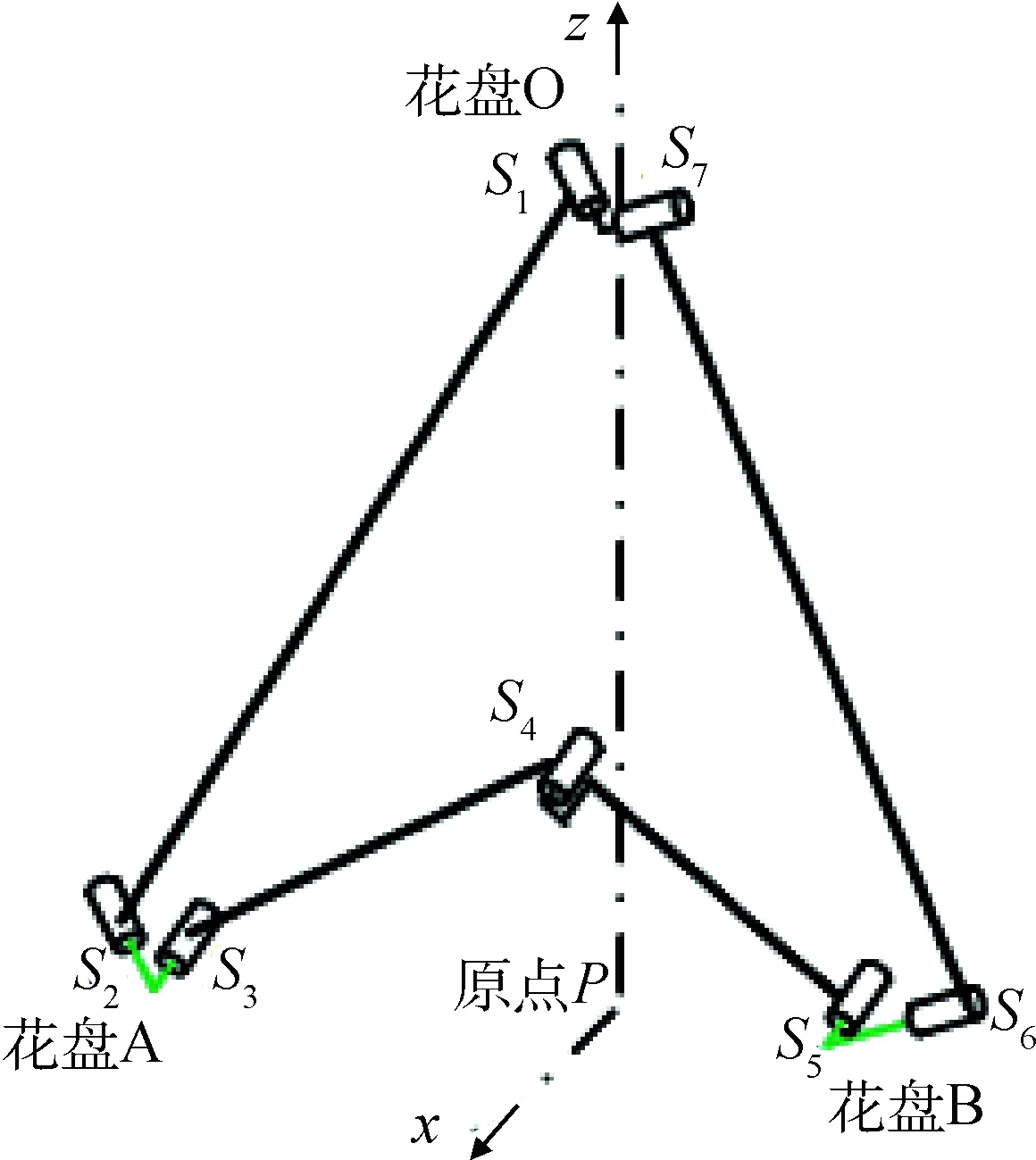
圖4 單閉環(huán)機構(gòu)Fig.4 Single closed-loop mechanism

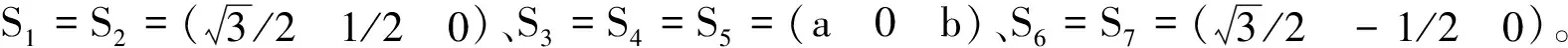
(2)

式中：(xiyizi)、(xjyj0)、(xkyk0)、(xm0zm)、(xk-yk0)、(xj-yj0)、(xi-yizi)分別為鉸鏈S1～S7中心位置的坐標。

根據(jù)螺旋理論[17，19]，約束螺旋與運動螺旋的互易積為0，即

$°$r=0

(3)

式中：$為運動螺旋；$r為約束螺旋；“°”代表兩旋量的互易積符號。

當構(gòu)架式天線轉(zhuǎn)動副軸線S3、S4、S5不平行于ABC平面，此時b≠0，由式(2)與式(3)可求得此單閉環(huán)機構(gòu)的約束螺旋$r=(0 0 0;0 0 0)，可知此單閉環(huán)單元無公共約束，則單閉環(huán)單元的公共約束數(shù)為λ=0，單閉環(huán)單元的階數(shù)d=6-λ=6。此時，單閉環(huán)單元的自由度為[17]：

M=n-dl=7-6×1=1

(4)

式中：M為機構(gòu)自由度數(shù)；d為單元階數(shù)。

2.2 二閉環(huán)機構(gòu)的自由度及過約束分析

再次分析整個二閉環(huán)機構(gòu)，二閉環(huán)機構(gòu)可視為并聯(lián)機構(gòu)，由3條支鏈Z1、Z2、Z3組成，如圖5所示。支鏈Z1由鉸鏈1～5及其鉸鏈之間的桿組成，支鏈Z2由鉸鏈6～7及其桿件組成，支鏈Z3由鉸鏈8～12及其桿件組成。將花盤O作為靜平臺，花盤B作為動平臺。支鏈Z1的運動螺旋系為：

(5)

支鏈Z2的運動螺旋系為：

(6)

支鏈Z3的運動螺旋系為：

(7)

其中支鏈Z1和支鏈Z2的運動螺旋在第2.1節(jié)已求出。

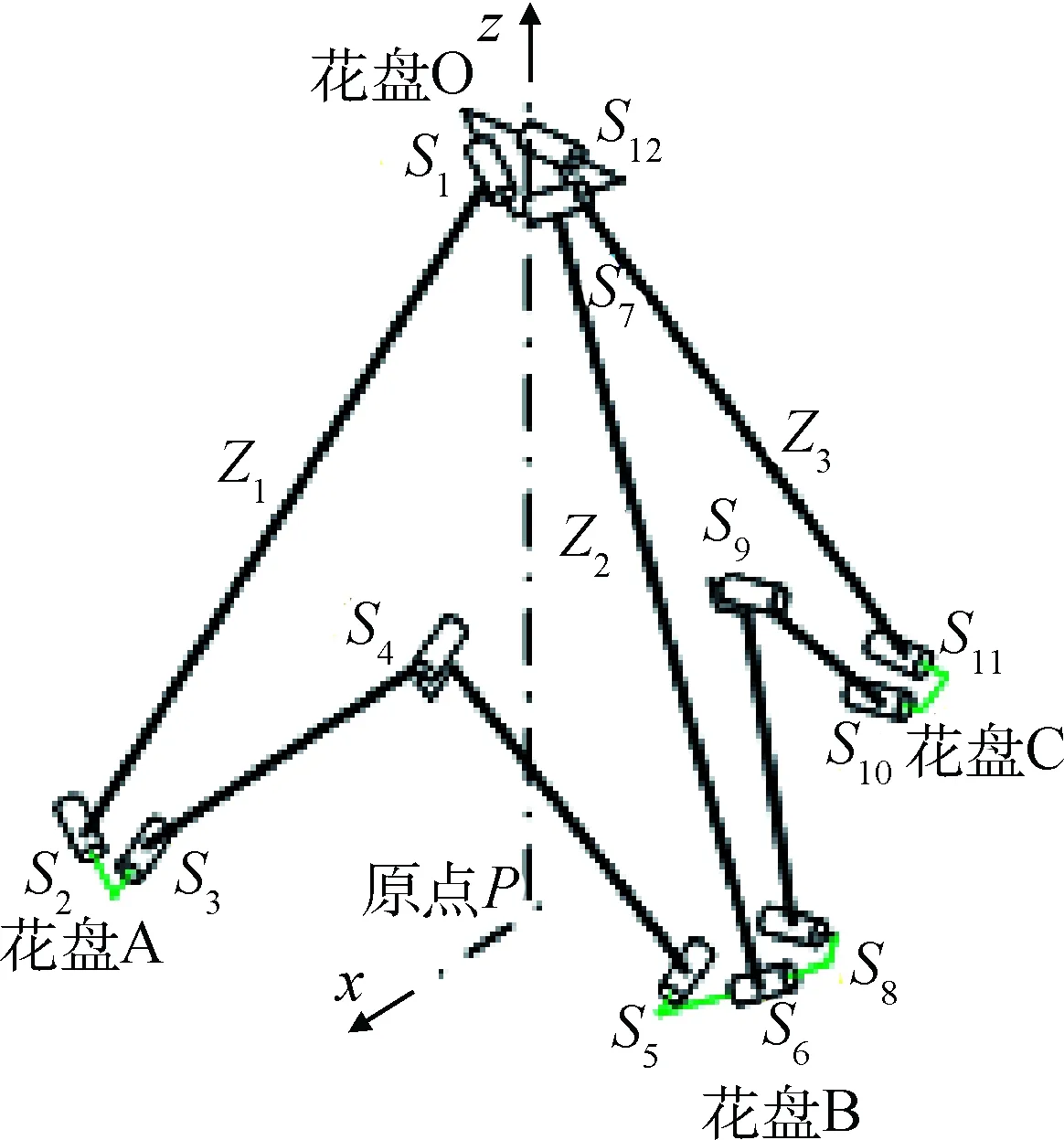
圖5 二閉環(huán)機構(gòu)Fig.5 Two closed-loops mechanism

由式(3)可知，支鏈Z1的約束螺旋為：

(8)

支鏈Z2的約束螺旋為：

(9)

(10)

因此二閉環(huán)機構(gòu)受到6個約束旋量，且沒有公共約束λ=0，則階數(shù)與單閉環(huán)單元一樣d=6-λ=6。二閉環(huán)單元受到4個約束力偶和2個約束力，其中4個約束力偶的最大無關(guān)數(shù)為3[20]，則動平臺B受到5個線性不相關(guān)的約束，因此二閉環(huán)機構(gòu)約束螺旋是五系螺旋結(jié)構(gòu)即k=5，且含有過約束。過約束個數(shù)為[7]：

(11)

式中：qi為第i支鏈約束螺旋的數(shù)目；λ為公共約束數(shù)目；p為支鏈數(shù)目。

由修正的Kutzbach-Grübler[17]公式可得到二閉環(huán)機構(gòu)的自由度為：

6×(11-12-1)+12+1-0=1

(12)

式中：fi為第i個運動副的相對自由度數(shù)；ν為多環(huán)并聯(lián)機構(gòu)在去除公共約束的因素后的過約束的數(shù)目；ζ為機構(gòu)中存在的局部自由度。

二閉環(huán)單元的自由度為1，則此四面體單元的自由度也為1。將式(8)、式(9)、式(10)代入式(2)中，再次求約束螺旋的反螺旋，可得到運動平臺B的運動螺旋為：

(13)

通過上述分析，二閉環(huán)機構(gòu)含有1個過約束，且此過約束為約束力偶。兩桿件有3個轉(zhuǎn)動副即含有3個運動螺旋且對機構(gòu)運動無影響，對照二閉環(huán)中的旋量$3、$4、$5，兩桿件的3個運動螺旋獨立，因此兩桿件含有3個約束螺旋即含有3個過約束，則四面體單元為4過約束機構(gòu)。

3 四面體單元的奇異分析

3.1 特殊位形下的奇異特性

在設(shè)計構(gòu)架可展開天線各部件結(jié)構(gòu)時，應(yīng)分析出3RR-3RRR單元的奇異性，可避免奇異特性導(dǎo)致的收展不協(xié)調(diào)性。對四面體單元進行約束奇異分析時，基于螺旋理論判定線矢量不同幾何空間的線性相關(guān)性來分析四面體單元的奇異性[21]。

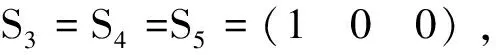
(14)

5×(11-12-1)+12+0-0=2

(15)

此位形下自由度與第2.2節(jié)中b≠0時相比多了1個自由度，這種奇異特性被稱為約束奇異，位形如圖6所示。

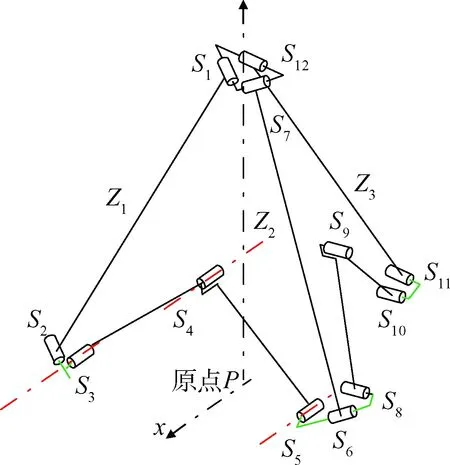
圖6 奇異位形Fig.6 Singularity configuration

3.2 自由度瞬時性判別

計算出在b=0位形下有2個自由度后，還須判斷自由度的瞬時性，若為瞬時自由度，則應(yīng)當舍去。此位形下對式(9)和式(14)求其反螺旋，求得B的運動螺旋為：

(16)

4 多單元組網(wǎng)自由度分析

構(gòu)架式天線各四面體單元采用共用花盤的方式聯(lián)接在一起，如圖7所示3個單元體兩兩共用一個花盤，把這樣的3個四面體單元所組成的機構(gòu)稱之為基本組合單元。

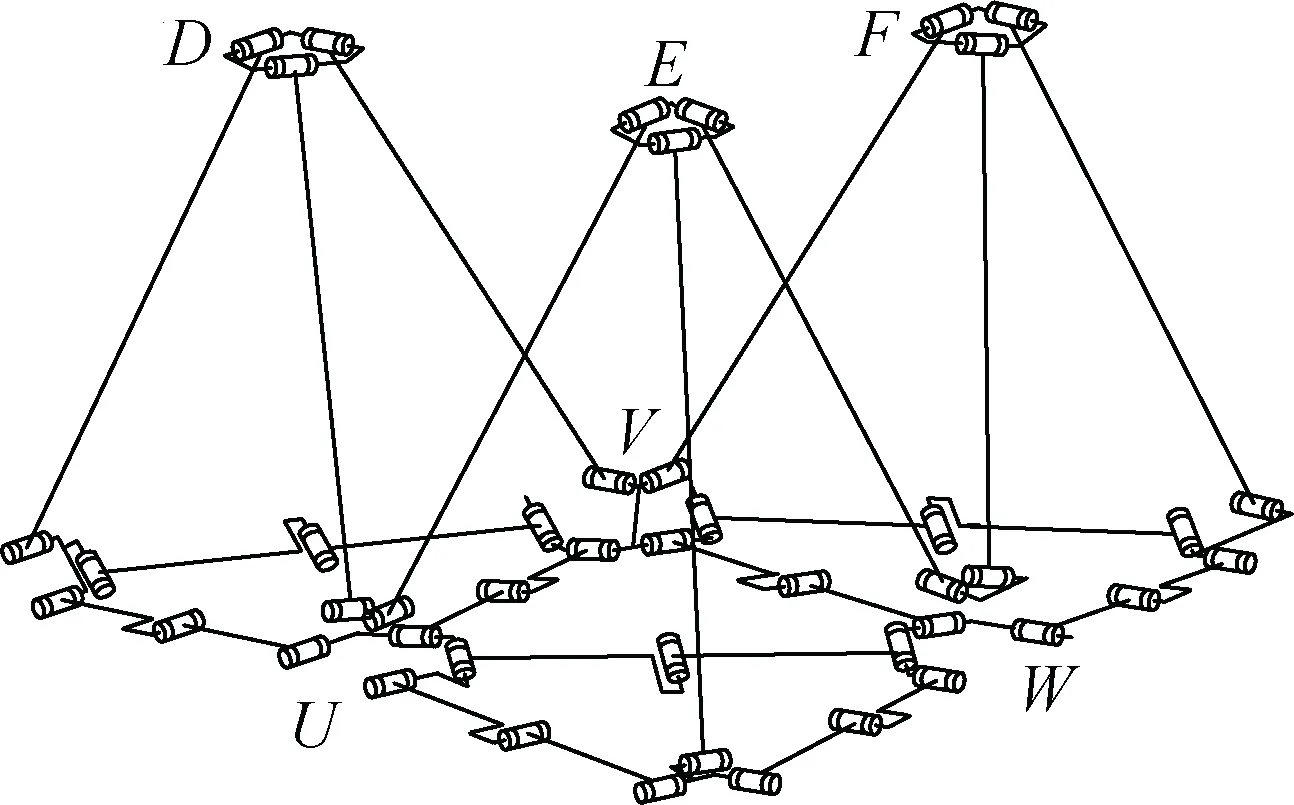
圖7 基本組合單元Fig.7 Basic combination unit

在計算多單元自由度時，此組合單元可以形成3個2RR-RRR單閉環(huán)構(gòu)成的機構(gòu)，如圖8(a)所示。該機構(gòu)可看成3個7R單閉環(huán)機構(gòu)組成，整個機構(gòu)在收展過程中，僅實現(xiàn)兩相鄰花盤的收縮或遠離移動，并不影響花盤在單元自身的運動約束。由第2.2節(jié)可知單閉環(huán)機構(gòu)的自由度為1，實現(xiàn)底面兩花盤的相對運動為一維移動，因此可將3個單閉環(huán)機構(gòu)等效為3個P副平面閉環(huán)機構(gòu)，如圖8(b)所示。

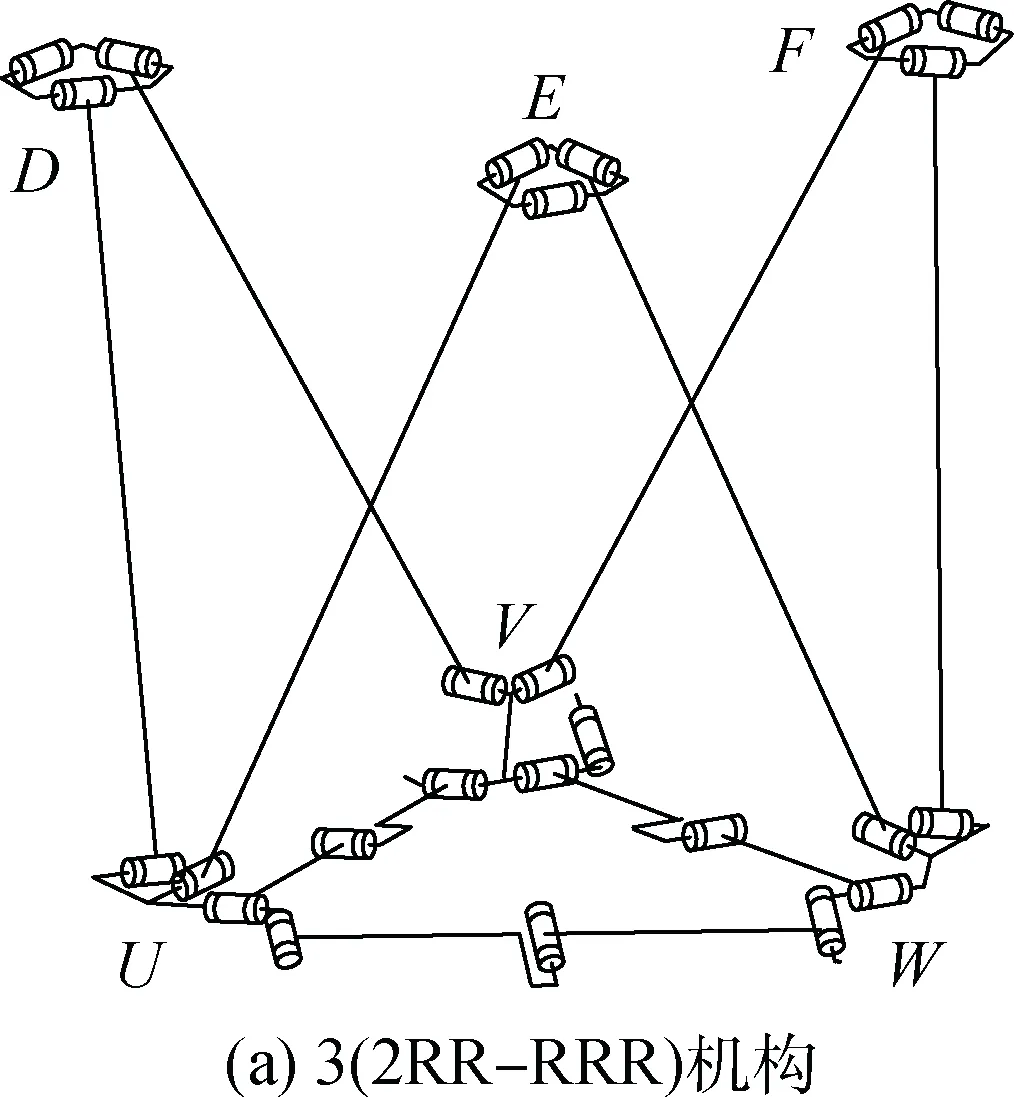
圖8 機構(gòu)等效Fig.8 Equivalent mechanisms

該機構(gòu)也可看成一個兩支鏈并聯(lián)機構(gòu)，把花盤3看成定平臺，花盤1看成動平臺，則兩支鏈分別為包含移動副的P1和P2P3支鏈。在花盤3中心建立參考坐標3-xy，則P1支鏈的約束螺旋為：

(17)

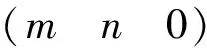
P2P3支鏈的約束螺旋為：

(18)

由此可知該等效機構(gòu)含公共約束為：

(19)

則λ=1，由于是平面機構(gòu)，d=3-λ=2，由式(4)可知3P副機構(gòu)的自由度為1。對上述支鏈的約束螺旋求反螺旋可得花盤1的運動螺旋為：

(20)

因此，基本組合單元的自由度為1，且花盤1和花盤3能夠沿著固定方向相對運動，實現(xiàn)展開收攏運動。

當天線在收展時，3個上花盤節(jié)點D、E、F在運動過程中各節(jié)點沿著兩節(jié)點方向相對移動，但不穩(wěn)定。在桁架結(jié)構(gòu)中，應(yīng)盡可能地避免局部模態(tài)，考慮到多層的桁架機構(gòu)具有更好的結(jié)構(gòu)剛度，要使機構(gòu)的每一個閉環(huán)都是封閉的，這樣才能形成一個穩(wěn)定的結(jié)構(gòu)體。而連接支鏈一般采用構(gòu)型為SRS支鏈、SPS支鏈、SRU支鏈或UPS支鏈，為使結(jié)構(gòu)簡單和對稱，選擇SRS支鏈為上花盤聯(lián)接的約束支鏈，構(gòu)型為3(3RR-3RRR)-3SRS，如圖9所示。此時SRS支鏈還有6個自由度，相當于虛約束不會對原來的基本組合單元運動產(chǎn)生影響，使收展運動協(xié)調(diào)。綜上可知，由3RR-3RRR四面體組成的構(gòu)架式可展開天線的自由度為1。

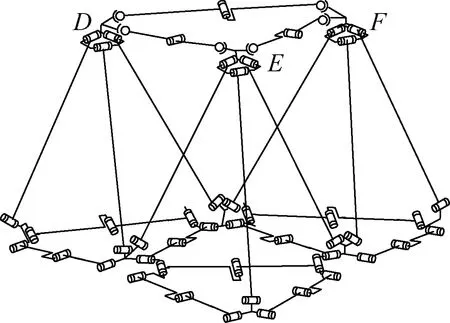
圖9 3(3RR-3RRR)-3SRS機構(gòu)Fig.9 3(3RR-3RRR)-3SRS mechanism

5 多單元花盤間距變化

為更好研究構(gòu)架式天線的展開特性，驗證由3RR-3RRR單元組成的構(gòu)架式天線為單自由度天線和運動協(xié)調(diào)性，可對基本組合單元進行運動學(xué)分析。因為上花盤連接支鏈為6自由度支鏈，不影響機構(gòu)的運動，在分析時上花盤支鏈同樣可省略。將天線中的花盤簡化成一個具有姿態(tài)的剛性點構(gòu)件進行分析，如圖10所示。3個收攏單元的3個底面分別繞三角形UVW的邊UV、VW和UW偏轉(zhuǎn)β，令底花盤V固定，在V點建立參考坐標系V-xyz，輸入為同步兩連桿的轉(zhuǎn)角大小θ。

圖10 收展機構(gòu)運動學(xué)分析簡圖Fig.10 Kinematics analysis of combination unit

L、M和N的位置矢量分別為:

(21)

(22)

(23)

進一步可得出特征單元的L、M、N3個外側(cè)節(jié)點兩兩間的相對距離變化，如圖11所示。

圖11 L、M、N3個外側(cè)節(jié)點間距變化Fig.11 Three outer nodes L，M，N spacing

由于仿真模型為根據(jù)布置于球面的等邊三角形而劃分得到的機構(gòu)，3個外側(cè)節(jié)點具有很好的對稱性，由圖11可看出在收攏過程中單元的3個外側(cè)節(jié)點L、M、N之間的相對距離曲線重合，并且節(jié)點之間互相靠近收縮，實現(xiàn)了在單輸入驅(qū)動下運動輸出構(gòu)件收攏的期望運動，并驗證了由3RR-3RRR單元組成的構(gòu)架式天線在收展過程中運動的協(xié)調(diào)性。

6 結(jié)束語

本文基于螺旋理論對組成構(gòu)架式可展開天線的3RR-3RRR四面體單元構(gòu)型綜合，得到了具有收展運動特性的單自由度機構(gòu)，并可在設(shè)計階段指導(dǎo)四面體單元結(jié)構(gòu)的設(shè)計，避免奇異性帶來收展不協(xié)調(diào)的影響。多單元組網(wǎng)后，反射器桁架系統(tǒng)依然是單自由度結(jié)構(gòu)，可實現(xiàn)對桁架天線的可控展開，并驗證了構(gòu)架式天線整體在工作時能收攏或完全展開，為其展開控制與展開動力學(xué)等后續(xù)研究提供堅實基礎(chǔ)。在工作實踐中，對構(gòu)架式天線反射器自由度和奇異特性的研究有利于構(gòu)架式空間可展開天線的結(jié)構(gòu)設(shè)計和研究，并且可運用于其他空間可展機構(gòu)，具有較強的應(yīng)用性。