輸送帶跑偏對驅動滾筒可靠性和優化設計的影響

樊智敏，尹兆明，馬秋艷

（1.青島科技大學 機電工程學院，山東 青島 266061；2.青島市技師學院 軌道交通學院，山東 青島 266229）

帶式輸送機作為重要的散裝物料輸送設備，因結構簡單、可靠性強、維護方便、費用低廉而被廣泛應用于煤礦、石油、化工等領域。帶式輸送機工作時，以輸送帶作為牽引和承載構件，輸送帶由與驅動滾筒間的摩擦力驅動。驅動滾筒是帶式輸送機的重要構件，其運行的安全穩定性在整個輸送機系統中具有舉足輕重的作用[1]。帶式輸送機由于在制造、安裝和使用等方面存在一些問題，使輸送帶經常出現跑偏現象[2]。輸送帶作為柔性元件在動力學上表現為顯著的粘彈性，在工作過程中存在粘彈性、大位移和大變形的耦合作用，能改變驅動滾筒的受力情況，導致其傳動精度下降，并加快其疲勞損壞[3-4]。目前，驅動滾筒設計一般采用許用應力法、經驗公式法和類比法，忽略輸送帶跑偏的影響，并常常通過增大安全倍數提高可靠性，這不僅會增大驅動滾筒的結構尺寸、質量和制造成本，而且使其可靠性與優化設計的計算結果存在較大誤差[5]。

本工作以帶式輸送機驅動滾筒為研究對象，利用SolidWorks軟件建立驅動滾筒實體模型，將其導入到Ansys Workbench有限元分析軟件中，對比分析輸送帶在正常運行工況和跑偏工況下驅動滾筒的受力情況及驅動滾筒設計變量對目標函數的靈敏度等，研究輸送帶跑偏對驅動滾筒可靠性和優化設計的影響，為驅動滾筒優化設計和可靠性提高提供科學依據，避免設計的盲目性。

1 驅動滾筒受力分析

輸送帶跑偏是帶式輸送機運行過程中最常見的現象，導致輸送帶跑偏的原因很多，本研究以驅動滾筒軸線偏移引起的跑偏為例進行分析。驅動滾筒作為帶式輸送機的主要受力構件，不僅承受自身重力、輸送帶張力和軸端輸入轉矩，還承受與輸送帶簡的摩擦力作用。

1.1 輸送帶跑偏時驅動滾筒的周向受力

在輸送帶跑偏工況下，驅動滾筒圓周方向上的受力如圖1所示。

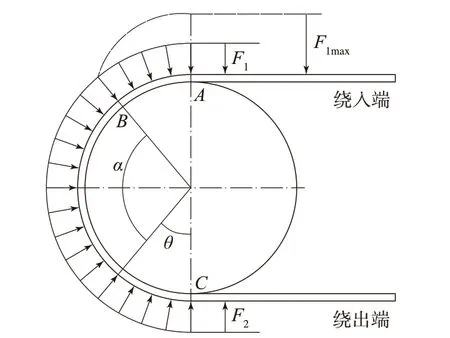
圖1 驅動滾筒周向受力分析

本工作主要研究驅動滾筒的應力應變情況，假設驅動滾筒上輸送帶張力不存在靜止弧，滑動弧占滿整個圍包角[6]。由帶式輸送機的傳動理論和歐拉公式可知，在包角α范圍內，輸送帶上任意一點張力（Fθ）為

式中，F2為輸送帶繞出端的張力，N；μ為輸送帶與驅動滾筒之間的摩擦因數；θ為輸送帶與驅動滾筒分離點至繞出的弧度，rad。

驅動滾筒在θ處單位表面受到輸送帶對其產生的面壓力（Pθ）為

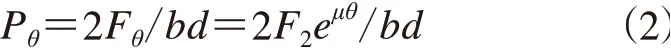
式中，b為輸送帶寬度，mm；d為驅動滾筒直徑，mm。

驅動滾筒在θ處單位表面受到的摩擦力（fθ）為

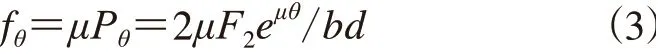
1.2 輸送帶跑偏時驅動滾筒的軸向受力

在輸送帶跑偏工況下，驅動滾筒軸線方向上的受力如圖2所示。輸送帶與驅動滾筒之間的張力（P）可分解為使輸送帶橫向移動的軸向力（P1）和使輸送帶縱向運行的驅動力（P2）。

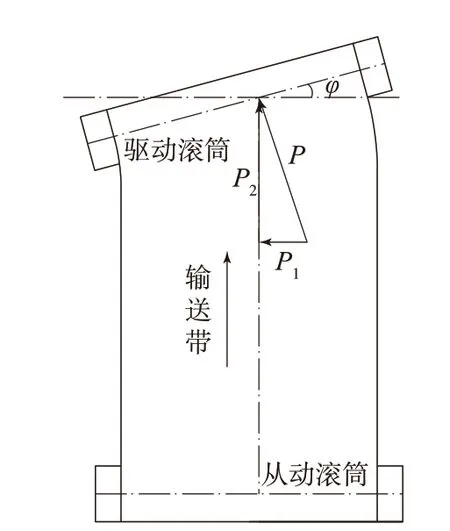
圖2 驅動滾筒軸向受力分析

式中，φ為驅動滾筒軸線偏移角。

由式（4）知，軸向力的大小由輸送帶與驅動滾筒之間的張力和驅動滾筒軸線偏移角度決定。當軸向力不小于輸送帶與驅動滾筒之間的極限摩擦力時，輸送帶會出現跑偏現象；當軸向力小于該極限摩擦力時，輸送帶雖不會出現跑偏現象，但在驅動滾筒上一直存在軸向力的作用。

2 輸送帶跑偏對驅動滾筒可靠性的影響

2.1 驅動滾筒的幾何參數和材料參數

以某型號等截面雙端驅動滾筒為例進行分析。主要構件的尺寸參數（mm）為：筒體長度1 600，帶寬 1 400，輻板間距 1 200，筒殼外直徑 1 670，筒殼厚度 38，輻板內直徑 695，輻板厚度 60，輪輻內直徑 495，輪輻寬度 170，軸總長度 2 566，軸承寬度 500，軸端外直徑200。載荷參數為：合力 1 200 kN，扭矩 280 kN·m，帶速 0.3 m·s-1，摩擦因數 0.3，包角

180°，跑偏時軸向力 300 kN，正常運行時軸向力為零。筒殼、滾筒軸、輪輻和輪轂的鋼材牌號分別為Q235，45#，ZG25和ZG25；滾筒軸的彈性模量為1.93×105MPa，其他3個部件均為2.0×105MPa；筒殼和滾筒軸的泊松比為0.28，輪輻和輪轂為0.30；密度均為7.85 Mg·m-3。

2.2 驅動滾筒模型的建立

輸送帶跑偏時，驅動滾筒受力情況比較復雜，為提高計算效率，需在有限元分析之前對帶式輸送機虛擬樣機進行簡化處理：（1）將構件的倒角、圓角、孔、槽、凸臺等特征進行壓縮；（2）假設整個驅動滾筒的焊縫工藝合格；（3）簡化軸承，用等效約束代替；（4）將一些不影響整體結構性能的小零件如密封圈、螺母、起吊螺栓等壓縮掉；（5）輸送帶在驅動滾筒筒殼的整個圍包弧上無滑動現象，圓周力的傳遞符合歐拉公式[7-9]。

根據驅動滾筒主要零部件參數，結合簡化處理結果，運用SolidWorks三維軟件對驅動滾筒進行建模。將創建好的模型導入到Ansys Workbench有限元分析軟件中，根據驅動滾筒的材料屬性定義，對驅動滾筒模型進行網格劃分，如圖3所示。

圖3 驅動滾筒的網格模型

2.3 兩種工況下驅動滾筒應力應變對比分析

根據驅動滾筒在正常運行和跑偏兩種工況下的受力情況施加約束和載荷，并對其應力應變情況進行對比分析。

2.3.1 位移變形分析

驅動滾筒位移變形對比如圖4所示。

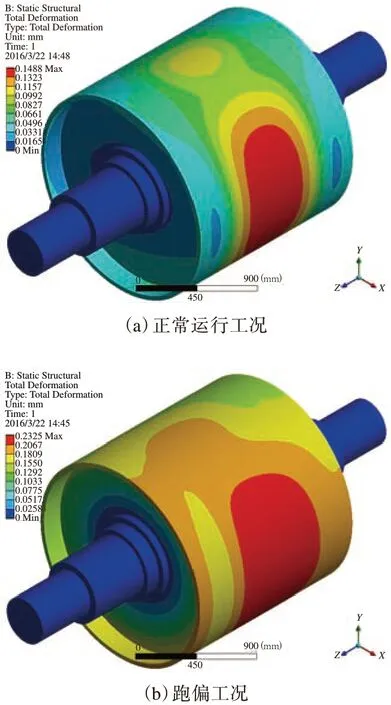
圖4 驅動滾筒位移變形對比

由圖4可知，帶式輸送機驅動滾筒在兩種工況下運行時，驅動滾筒的最大變形均出現在輸送帶與筒殼接觸的中心部位。輸送帶在正常工況下運行時，驅動滾筒筒殼的最大變形量為0.149 mm，兩側的變形量呈對稱分布。輸送帶在跑偏工況下運行時，驅動滾筒筒殼的受力情況發生變化，整體變形量相對較大，筒殼的最大變形量為0.233 mm，且輸送帶跑偏一側的變形量相對較大，呈不均勻分布。對比兩種工況下驅動滾筒的位移變形情況可知，輸送帶跑偏不僅會使驅動滾筒筒殼的最大變形量增大，還能使其分布范圍擴大，且輸送帶跑偏一側筒殼的變形量相對較大。

2.3.2 等效應力分析

驅動滾筒等效應力分布對比如圖5所示。

由圖5（a）可知，輸送帶在正常工況下運行時，驅動滾筒筒殼的最大應力出現在兩側輻板與筒殼的接觸處，其值為18.915 MPa，且兩側應力大小呈對稱分布。由圖5（b）可知，輸送帶在跑偏工況下運行時，在輸送帶跑偏一側筒殼與輻板接觸處和輪轂與輻板接觸處的應力相對較大，其最大值為28.845 MPa。對比可知，輸送帶跑偏時，在驅動滾筒上產生的最大應力值較大，且輸送帶跑偏一側的整體應力值明顯高于另一側，說明輸送帶跑偏不僅能使驅動滾筒的最大應力增大，而且還能使其出現的位置發生改變。

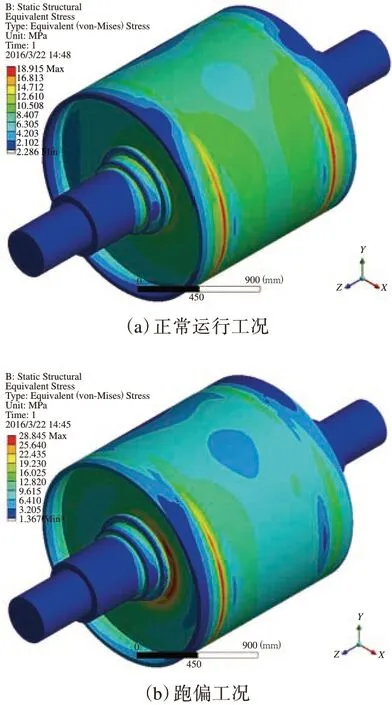
圖5 驅動滾筒等效應力分布對比

2.4 軸向力對驅動滾筒應力應變分布的影響

由式（4）可知，驅動滾筒的偏移角度不同，與輸送帶間產生的軸向力值也不相同。通過分析得到軸向力變化對驅動滾筒最大應力和最大變形量的影響，如表1所示。

由表1可知，隨著軸向力的增大，驅動滾筒最大應力和最大變形量的值也逐漸增大。軸向力小于100 kN時，驅動滾筒最大變形量的變化幅度較小；軸向力大于100 kN時，其變化幅度增大，且隨著軸向力的增大，驅動滾筒上最大變形量的分布范圍也逐漸擴大。軸向力小于450 kN時，驅動滾筒最大應力的變化幅度較小；軸向力大于450 kN時，其變化幅度相對較大，且隨著軸向力的增大，驅動滾筒上出現最大應力的位置也逐漸發生變化。軸向力較小時，驅動滾筒的最大應力出現在兩側輻板與筒殼的接觸處；隨著軸向力的增大，驅動滾筒上出現最大應力的位置轉移到輸送帶跑偏一側輻板與筒殼的接觸處；當軸向力增大到一定值后，驅動滾筒的最大應力同時出現在輸送帶跑偏一側輻板與筒殼和輪轂的接觸處。

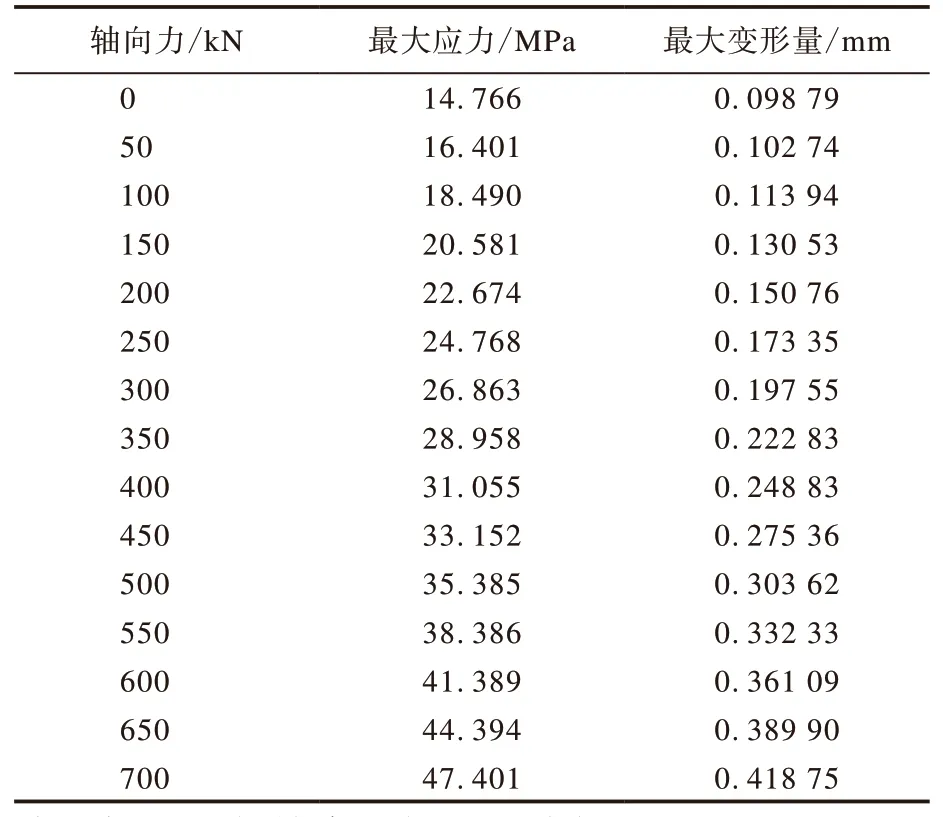
表1 軸向力對驅動滾筒最大應力和最大變形量的影響

3 輸送帶跑偏對驅動滾筒優化設計的影響

在正常運行工況下，由于輸送帶的物理特性，其與驅動滾筒間始終存在較小的軸向力，使其產生小幅偏移，影響相關零部件的使用壽命。因此，在對驅動滾筒進行優化設計時需要考慮輸送帶跑偏的影響。

3.1 兩種工況下的靈敏度對比

通過對驅動滾筒應力應變的有限元分析可知，輸送帶跑偏會對驅動滾筒筒殼、輪轂和輻板的應力應變產生較大的影響，因此選取驅動滾筒輻板厚度、輻板間距、筒殼厚度和輪轂寬度為設計變量，以驅動滾筒的最大變形量、最大應力和質量為目標函數。輻板厚度、輻板間距、筒殼厚度和輪轂寬度的初始值（上限/下限，mm）分別為60（70/50），1 200（1 500/900），38（44/32）和170（190/150）。

在靈敏度分析中，設計變量對目標函數靈敏度的絕對值越大，對目標函數的影響越大。靈敏度為正值，表示參數增大時目標函數值相應增大；靈敏度為負值，表示當參數減小時目標函數值相應減小[10]。通過分析得到兩種工況下驅動滾筒所選設計變量對目標函數的靈敏度，如表2所示。

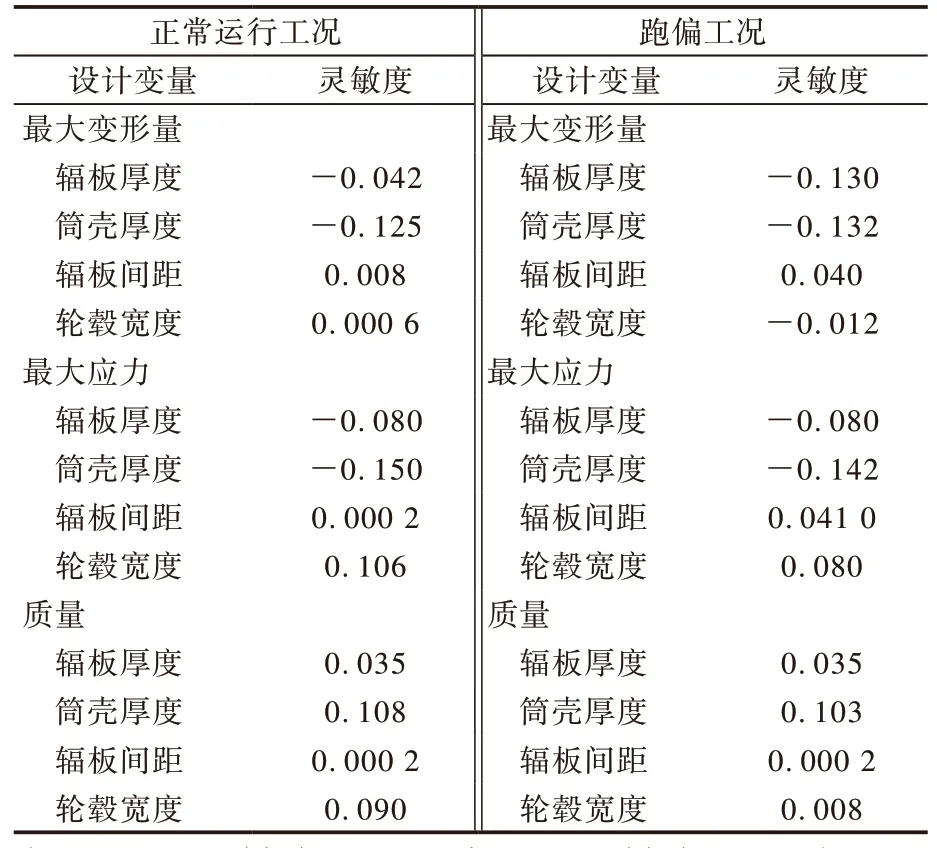
表2 設計變量對目標函數的靈敏度

對比可知，在輸送帶跑偏工況下，各設計變量對驅動滾筒最大應力和最大變形量的靈敏度影響明顯增強，對質量的靈敏度無變化，說明輸送帶跑偏影響所選設計變量對驅動滾筒最大應力和最大變形量的靈敏度，而對質量的靈敏度無影響。此外，在兩種工況下，輻板厚度和筒殼厚度對驅動滾筒目標函數靈敏度的影響相對較大，因此在對驅動滾筒進行優化設計時，可選取輻板厚度和筒殼厚度為主要設計變量。

3.2 設計變量參數變化對目標函數的影響

由兩種工況下驅動滾筒設計變量對目標函數靈敏度的對比分析可知，無論輸送帶跑偏與否，驅動滾筒設計變量對質量的靈敏度是相同的。因此，僅考慮主要設計變量（筒殼厚度和輻板厚度）對驅動滾筒最大應力和最大變形量的影響。

（1）單個設計變量對驅動滾筒目標函數的影響分別如表3和4所示。

由表3和4可以看出，驅動滾筒的最大變形量和最大應力在兩種工況下隨筒殼厚度和輻板厚度增大的變化趨勢相似。在一定范圍內，隨筒殼厚度和輻板厚度的增大，驅動滾筒的最大變形量均逐漸減小，且在輸送帶跑偏工況下的變化幅度較大，而驅動滾筒的最大應力均先增大后減小，但兩種工況下的變化幅度相差不大。由此可見，輸送帶跑偏使驅動滾筒的最大變形量和最大應力增大，且在輸送帶跑偏工況下，隨筒殼厚度和輻板厚度的增大，最大變形量的變化幅度較大，最大應力的變化幅度與正常運行工況相差不大。

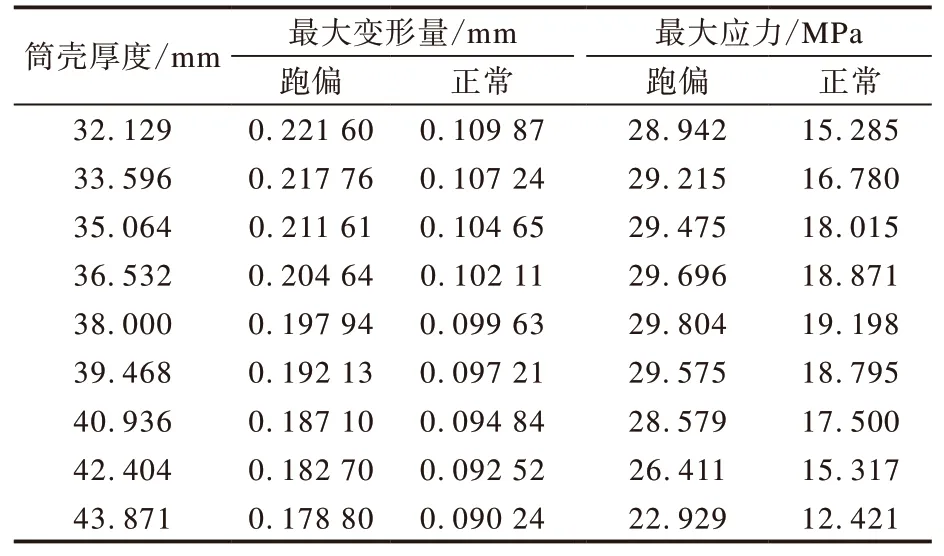
表3 筒殼厚度對驅動滾筒應力應變的影響

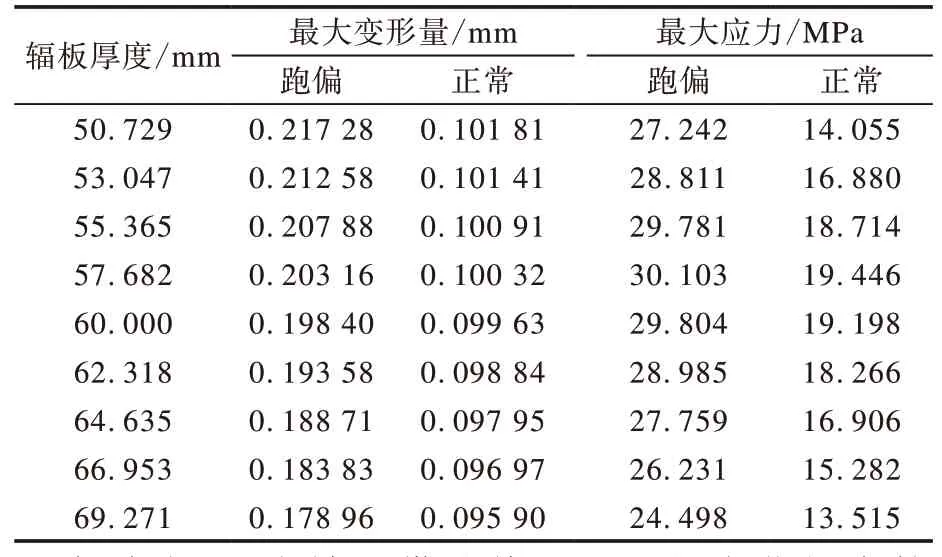
表4 輻板厚度對驅動滾筒應力應變的影響

（2）兩個設計變量同時變化對驅動滾筒目標函數的影響如圖6和7所示。

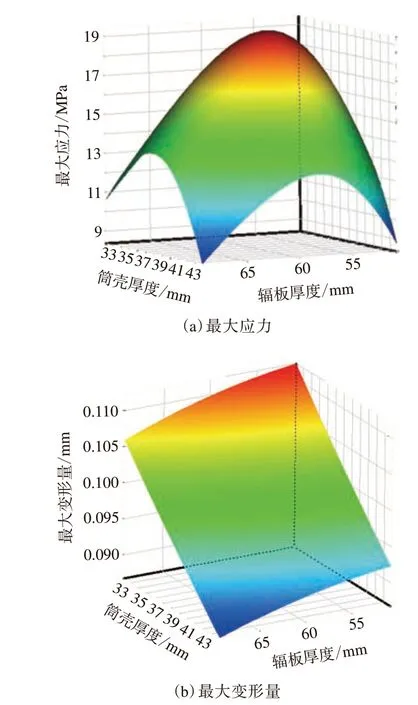
圖6 輸送帶正常運行工況下筒殼厚度和輻板厚度對驅動滾筒應力應變的影響

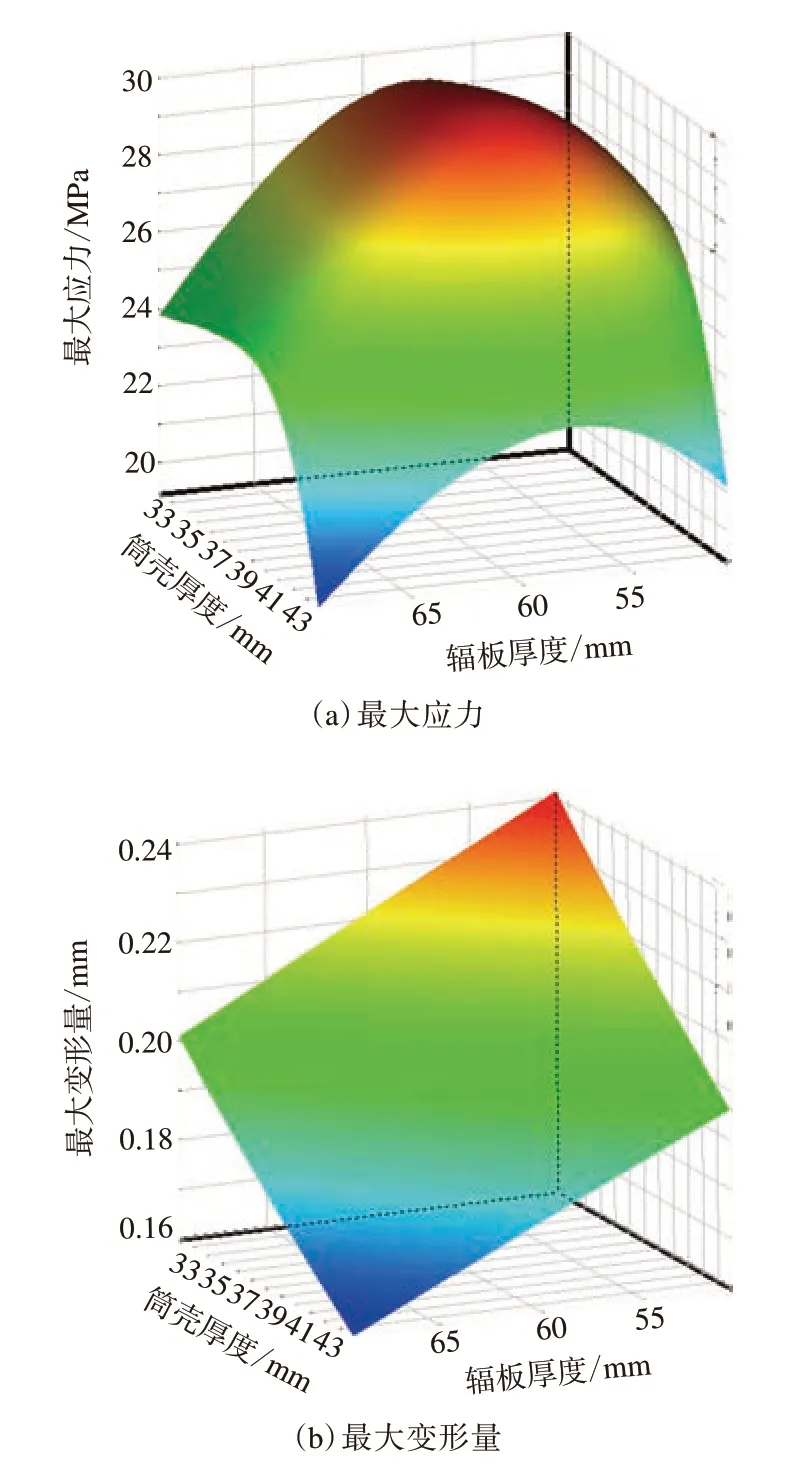
圖7 輸送帶跑偏工況下筒殼厚度和輻板厚度對驅動滾筒應力應變的影響

由圖6和7對比可知，在兩種不同工況下，同時改變輻板厚度和筒殼厚度會對驅動滾筒最大應力和最大變形量產生不同影響。相對正常運行工況，在輸送帶跑偏工況下，兩設計參數同時改變，驅動滾筒的最大應力和最大變形量均增大，其分布范圍也發生改變，最大應力的分布范圍擴大，最大變形量的分布范圍縮小。此外，僅改變某一設計變量，易使驅動滾筒產生應力集中，加速驅動滾筒的損壞。可見，輸送帶跑偏會改變設計變量對驅動滾筒應力應變的影響。因此，對驅動滾筒進行優化設計時，不僅應考慮多個設計變量的綜合影響，還應考慮運行過程中輸送帶跑偏的影響。

4 結論

（1）輸送帶跑偏使驅動滾筒的應力應變增大，最大應力和最大應變的分布范圍擴大，且隨輸送帶偏移量的增大，驅動滾筒所受軸向力增大，其應力應變隨之增大，分布范圍也發生變化。

（2）在輸送帶跑偏工況下，驅動滾筒在筒殼中央截面處及兩側輻板與筒殼和輪轂的接觸處易發生疲勞損壞，影響驅動滾筒的使用壽命。

（3）相對正常運行工況，在輸送帶跑偏工況下，設計變量對驅動滾筒最大應力和最大變形量的靈敏度增強，說明輸送帶跑偏改變設計變量對驅動滾筒應力應變的影響。

（4）輸送帶跑偏增大設計變量對目標函數的靈敏度，驅動滾筒是組合系統，僅改變某一設計變量易產生應力集中，影響使用壽命。在對驅動滾筒優化設計時，不僅應考慮多個設計變量的綜合影響，還應考慮運行過程中輸送帶跑偏的影響。