矩形靜壓推力軸承表面平面度與粗糙度的綜合分形模擬

張美紅，董皓，趙曉龍，劉波，張君安

(西安工業大學 機電工程學院，西安 710021)

1 引言

矩形靜壓推力軸承是根據氣體潤滑技術開發的精密機械元件，加工精度較高[1]。為從理論上分析此類軸承的潤滑性能，模擬其下表面微觀輪廓(圖1)是關鍵性的第1步。

圖1 矩形靜壓推力軸承下表面模型

目前，分形幾何作為一種新的數學理論，已被廣泛應用于表面微觀形貌的研究[2-3]。文獻[4]基于分形學中的Weierstrass-Mandelbrot函數建立了粗糙表面的分形模型，即M-B模型；文獻[5]提出了用于描述自然界隨機分形的分數布朗模型；文獻[6-7]則基于分形插值理論提出了分形插值曲面模型，利用曲面上的部分信息和特征擬合出曲面的整體形態。

為模擬矩形靜壓推力軸承下表面的真實輪廓形貌，結合軸承表面特征，利用分形插值曲面法對其表面平面度和粗糙度進行綜合分形模擬，為計算靜壓止推軸承的潤滑性能奠定基礎。

2 矩形靜壓推力軸承表面特征

盡管矩形靜壓止推軸承的表面加工精度很高，但從微觀角度，其表面形貌仍然由許多凸峰和凹谷組成，相鄰2個波峰或2個波谷之間的距離很小，肉眼難以區分。其中粗糙度輪廓波峰之間的距離通常小于1 mm，表面波紋度的波距通常為1～10 mm，幾何形狀輪廓(平面度誤差)的波距通常大于10 mm，且三者總是同時存在同一個表面。另外，矩形靜壓推力軸承表面多采用研磨的加工方式，研磨過程中會不同程度地出現邊緣塌邊現象[8]，從而使平面度誤差變大。因此，需要模擬一個同時具有平面度和粗糙度特征的軸承表面。

表面微觀形貌模擬通常有M-B模型、分數布朗模型以及分形插值模型。用10 mm×10 mm作為采樣區域，采樣間距為0.1 mm時，通過M-B模型、分數布朗模型所形成的表面輪廓如圖2所示。從圖中可以看出，對于這2種模型，參數一旦確定，表面形貌也唯一確定，且都表征的是表面粗糙度。分形插值模型則是利用曲面上的部分信息擬合出曲面的整體形貌，因此原始曲面形貌的變化會導致分形插值后曲面的幾何形狀也發生變化，且壓縮比的變化也會導致表面粗糙度的變化。基于同一原始曲面，選取不同的壓縮比α時得到的具有不同維數的粗糙表面形貌如圖3所示。

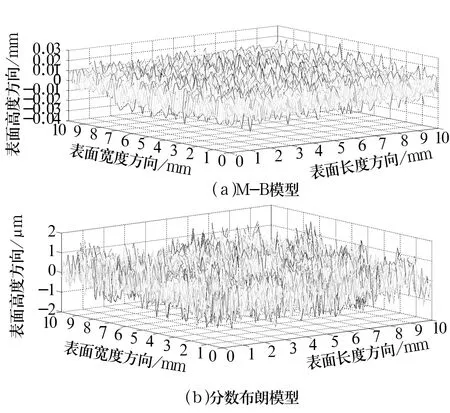
圖2 表面輪廓的模擬

因此，結合軸承表面特征及3種模型所模擬表面形貌的相互比較，選定分形插值模型來模擬矩形靜壓推力軸承下表面的微觀形貌。

3 矩形靜壓推力軸承表面模擬實例

3.1 原始曲面的建立

將軸承下表面平面度測量數據作為插值前的原始數據。傳統的平面測量為消除塌邊情形對結果的影響，在測量400 mm×400 mm的表面平面度時會在上下左右邊緣各留5 mm，共測25個點。為模擬塌邊情形，在傳統測量數據的基礎上另外測量了軸承表面邊緣的多組數據，結果見表1。基于表1中數據，需要進行插值的矩形靜壓推力軸承原始曲面如圖4所示，很明顯可以看出軸承表面邊緣有塌邊現象。

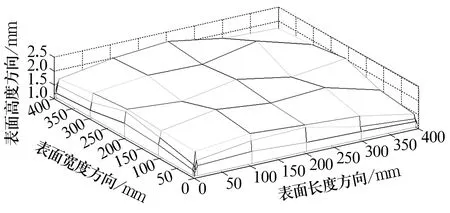
圖4 矩形靜壓推力軸承原始曲面

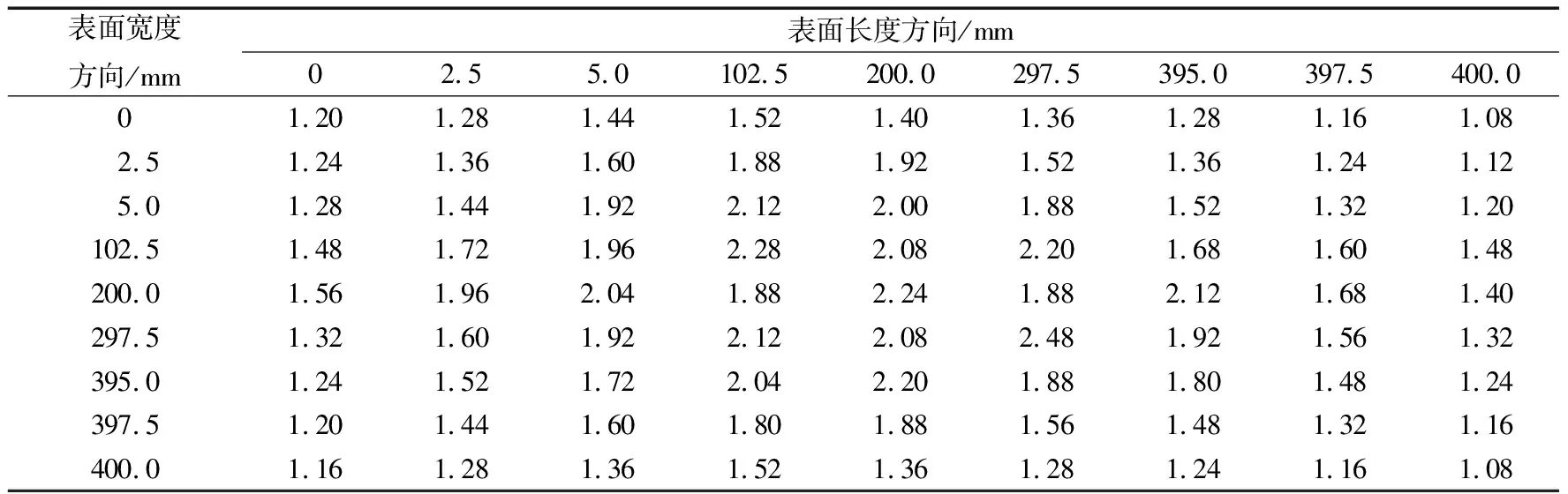
表1 矩形靜壓推力軸承下表面平面度測量數據

3.2 表面形貌的分區域插值模擬

如果將原始曲面進行整體分形插值，由于分形理論中自相似性特征的存在，分形插值后的表面形貌中間部分也會出現塌邊情形，與實際情況不符。因此采用分區域插值，即將原始曲面分為如圖5所示的9個區域，分別為中間部分、4個邊緣以及4個邊角，各區域的原始曲面如圖6所示。

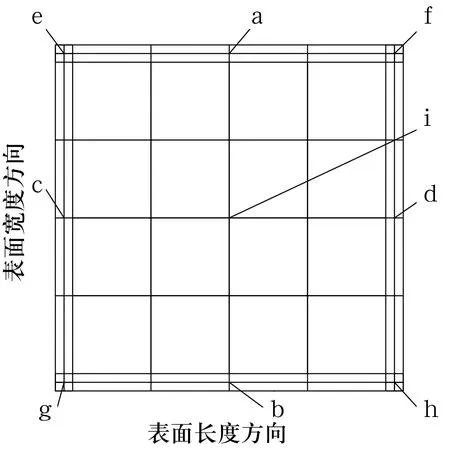
圖5 矩形靜壓推力軸承下表面的區域劃分

圖6 各區域的原始曲面

基于分形插值曲面數學理論，運用MATLAB將9個區域同時進行插值繪制出第1次插值后的曲面如圖7所示。

對于同一組插值數據，選取不同的垂直因子α值(壓縮比)，就可得到具有不同分形維數的粗糙表面。從圖7可以看出：垂直因子越小，平面度特征越明顯；垂直因子越大，表面越粗糙，隨著垂直因子的增大，粗糙度特征越來越明顯。

在第1次插值的基礎上，反復迭代從而得到不同程度的靜壓推力軸承分形插值曲面，垂直比例因子α=0.3時第2次及第3次插值所生成的曲面如圖8所示。

從圖7b和圖8可以看出，當垂直因子一定時，隨著插值次數的增大，粗糙度特征越來越明顯。且平面度(幾何形狀)特征和粗糙度特征可以同時顯現出來，完成了對靜壓推力軸承表面粗糙度和平面度的綜合模擬。

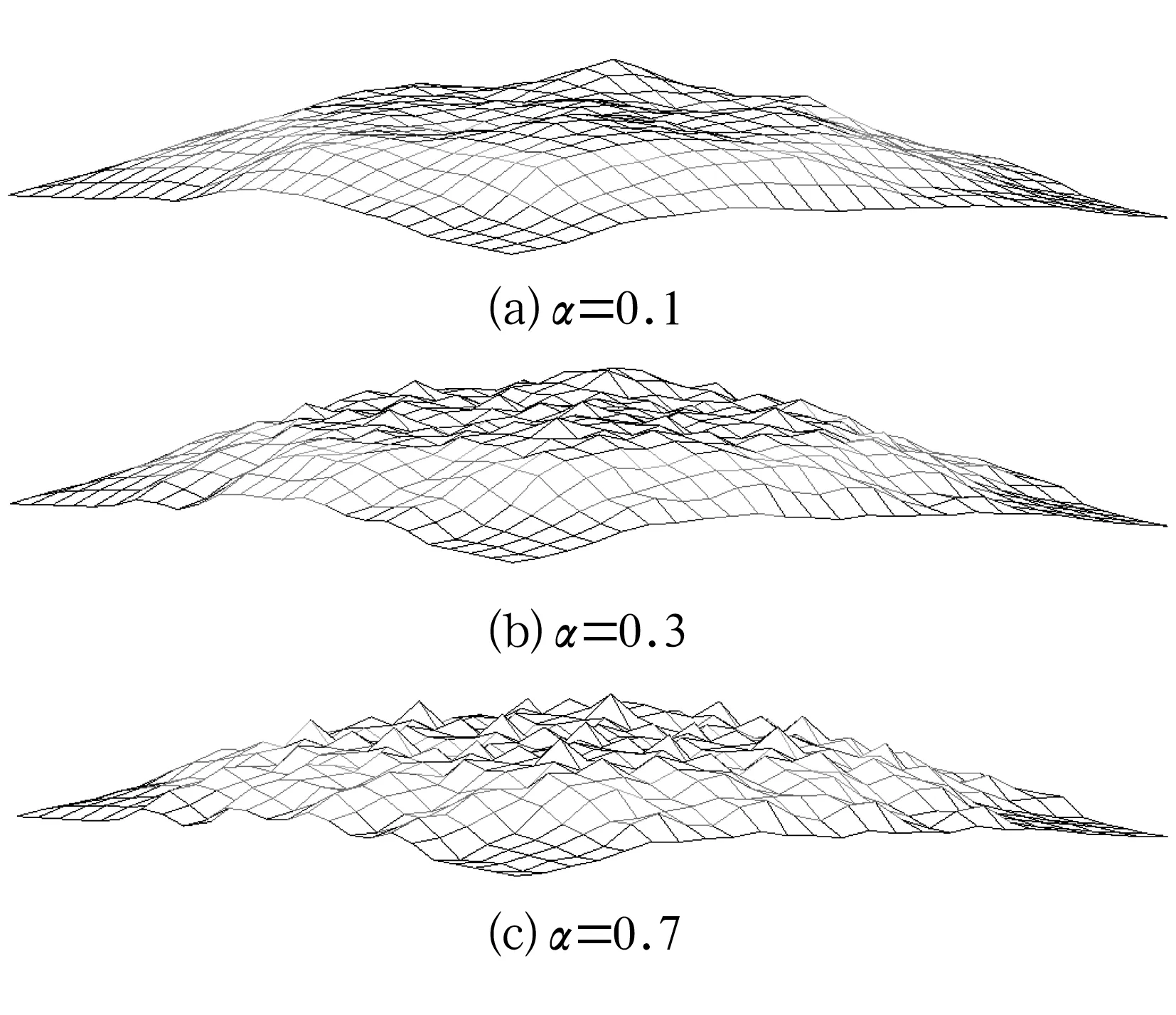
圖7 第1次插值后軸承下表面輪廓形貌

圖8 軸承下表面分形插值曲面(α=0.3)

為驗證該方法對矩形靜壓推力軸承表面邊緣塌邊情形的模擬是否符合實際情況，與利用電子水平儀[9]得到的軸承下表面平面度檢測結果(圖9)進行了對比。從圖中可以看出，軸承邊緣確實出現塌邊情形，說明結合平面度測量數據將原始數據進行分區域插值模擬出的邊緣塌邊符合真實情況。

圖9 軸承下表面平面度仿真圖

4 結束語

基于分形幾何學，結合矩形靜壓推力軸承的表面特征，選取分形理論中的分形插值模型對軸承下表面的微觀形貌進行了數值模擬，研究發現：

1)利用分形插值模型模擬出的軸承下表面形貌能夠同時反映出平面度及粗糙度特征。

2)將原始曲面數據進行分區域插值模擬可以避免軸承表面中間部分出現塌邊的情形，模擬結果接近軸承表面真實形貌。