組合重力場模型的精度及其適用性分析

馬艷鴿，郭春喜，張盼盼

(1.長安大學 地質工程與測繪學院，陜西 西安 710064；2.國家測繪地理信息局大地測量數據處理中心，陜西 西安 710054)

高分辨率、高精度的地球重力場模型在利用GNSS技術計算正常高中發揮重要的作用[1-2]。隨著衛星重力計劃的實施，重力場模型的精度和分辨率都得到很大改善，CHAMP、GRACE、GOCE等重力衛星使得全球重力場模型的中低階的精度提高兩個量級或者更高[3-4]。現階段主要的超高階重力場模型有EGM2008、GECO及EIGEN-6C4等，EGM2008利用地面重力數據、GRACE衛星重力數據、衛星測高數據等共同解算獲得[5]。GECO重力場模型由GOCE低階重力場模型TIM_R5聯合EGM2008得到，前0～359階利用GO_CONS_GCF_2_TIM_R5重力場模型的0～250階結合EGM2008重力場模型的0～359階計算得到，360～2 190階與EGM2008的360～2 190階保持一致[6]。EIGEN-6C4重力場模型利用地面重力數據、衛星重力數據(GOCE、GRACE、LAGEOS)、衛星測高數據等共同解算獲得[7]。而EGM2008和EIGEN-6C4重力場模型在解算的過程中除利用衛星測量的數據之外，還有一些地形數據或者地面重力數據，存在一些長波段的誤差，另外，GECO含有EGM2008模型的信息，同樣存在長波段的誤差，這些誤差會傳遞到重力場模型求解的高程異常中，從而影響所得高程異常的精度[8]。為解決這一問題，可利用純衛星重力場模型選擇合適的截斷階次替換高階重力場模型相對應的階次，純衛星重力模型完全由衛星數據獨立解算，不依賴地面重力數據，因此不受地面數據長波段誤差的污染。本文在分析EGM2008、GECO及EIGEN-6C4 3個超高階重力場模型計算高程異常精度的基礎之上選擇GOCO03S、GO_CONS_GCF_2_DIR_R5、GO_CONS_GCF_2_SPW_R2以及GO_CONS_GCF_2_TIM_R5等4個純衛星重力場模型實驗分析，選取合適的截斷階次確定組合重力場模型并對其進行精度分析，最后探討組合重力場模型在GNSS高程擬合中的應用。

1 原理與方法

1.1 模型的精度檢核

利用GNSS/水準數據進行重力場模型的精度檢核，計算P點的模型高程異常ξp，則GNSS/水準確定高程異常的方法為

ξGNSS/水準=H-h.

(1)

式中：H為GNSS實測的大地高；h為水準實測的正常高。可以得到殘差高程異常為

Δξ=ξp-ξGNSS/水準.

(2)

利用式(3)進行重力場模型的精度評定。

(3)

1.2 組合重力場模型的確定

超高階重力場模型EGM2008、GECO、EIGEN-6C4存在著由地面數據引起的長波誤差，因此選擇GOCO03S、GO_CONS_GCF_2_DIR_R5、GO_CONS_GCF_2_TIM_R5以GO_CONS_GCF_2_TIM_R5等4個純衛星重力場模型進行實驗分析，進一步選擇合適的模型的截斷階數替換EGM2008、GECO、EIGEN-6C4重力場模型相應的階數。主要步驟為：①選擇合適的純衛星重力場模型截斷階數N。②組合重力場模型的0～N階由純衛星重力場模型得到，N～2 190階由超高階重力場模型相應的階補充得到。因此，組合重力場模型的確定關鍵是模型的截斷階數的確定，截斷階數的確定是利用GNSS/水準數據檢核組合重力場模型的精度進行確定的，具體的步驟為：

1)對純衛星重力場模型選擇截斷階數k(k=10，20，30…N；N為純重力場模型的最大階數)，組成新的重力場模型，新模型的0～K階由純重力場模型獲取，K～2 190階由超高階重力場模型相應的階補充得到。

2)利用新的重力場模型計算GNSS點對應的模型高程異常，由式(2)計算殘差高程異常，然后由式(3)計算模型的精度。

3)選擇精度最高的模型為最終的組合重力場模型，其對應的階數k為最佳的截斷階數。

1.3 組合重力場模型在GNSS高程擬合中的應用

GNSS高程擬合的模型很多，本文以多面函數擬合模型進行GNSS高程擬合，GNSS高程多面函數擬合模型的基本原理是將殘差高程異常用多個曲面高度逼近，建立數學模型，借此可以求解未知點的高程異常[9]。多面函數的數學表達式可以表示為

(4)

式中:Δξi為高程異常值;ai為待定系數;Q(x,y,xi,yi)為核函數，本文選擇的核函數為雙曲面核函數，具體形式為

(5)

其中δ為光滑系數。

2 算例分析

本文選取長江南京段控制網數據進行重力場模型精度及適用性分析，總共有53個高精度的GNSS控制點，每個點位都有基于WGS-84坐標系下的大地坐標以及二等水準高程數據。圖1為點位分布圖。

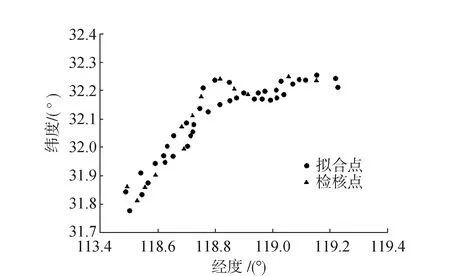
圖1 點位分布圖

2.1 超高階重力場模型精度分析

對EGM2008、GECO及EIGEN-6C4超高階重力場模型，分別計算53個GNSS控制點對應的模型高程異常，并與GNSS/水準實測的高程異常做比較，結果見表1。

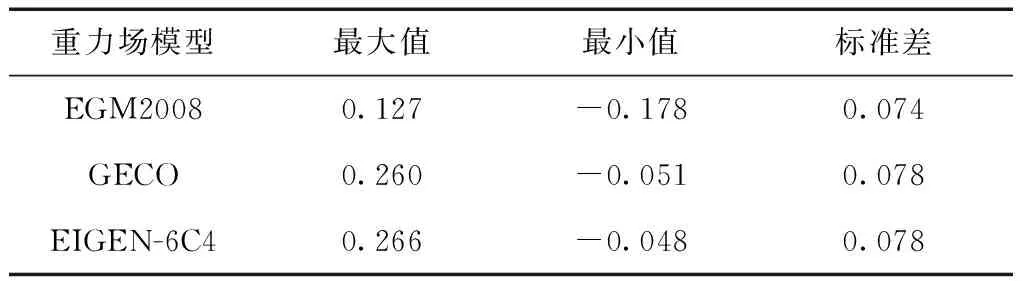
表1 超高階模型與GNSS/水準的高程異常比較結果 m

在本實驗區域，從表1可以看出： 3個超高階重力場模型的精度都達到了厘米級；EGM2008重力場模型的精度稍高于GOCE和EIGEN-6C4模型的精度。

2.2 組合重力場模型確定

組合重力場模型確定的關鍵是對純衛星重力場模型截取可靠的階次，對EGM2008、GECO及EIGEN-6C4超高階重力場模型利用純衛星重力場模型進行不同階次的組合，得到各自對應的組合重力場模型(例如：GOCO03S/ EGM2008、GOCO03S/ GECO、GOCO03S/ EIGEN-6C4等，具體表示純衛星重力場模型與超高階重力場模型的組合重力場模型)。利用1.2中的原理分別對EGM2008、GECO及EIGEN-6C4超高階重力場模型對應的組合重力場模型進行精度分析，精度結果分別見圖2—圖4。

圖2 EGM2008對應的組合重力場模型精度趨勢

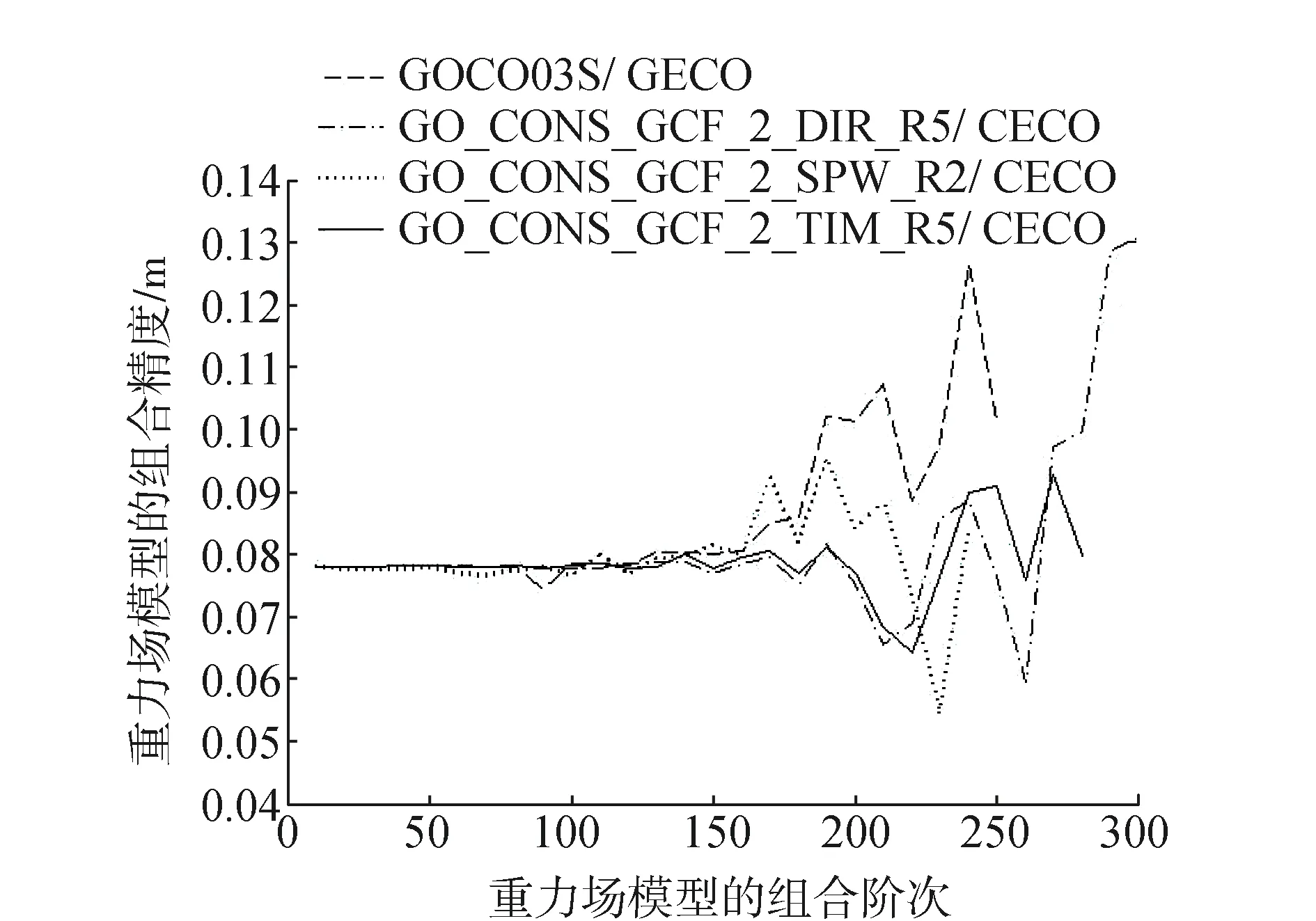
圖3 GECO對應的組合重力場模型精度趨勢

圖4 EIGEN-6C4對應的組合重力場模型精度趨勢

由圖2—圖4可以看出超高階重力場模型EGM2008、GECO及EIGEN-6C4對應的組合重力場模型在150階前的精度趨勢基本一致，在150階以后各組合重力場模型的精度趨勢表現出明顯的差異。可以選擇精度最高時對應的階次為組合模型的可靠截取階次，由圖2可以看出組合重力場模型GOCO03S/ EGM2008、GO_CONS_GCF_2_DIR_R5/EGM2008、GO_CONS_GCF_2_SPW_R2/EGM2008及GO_CONS_GCF_2_TIM_R5/EGM2008的可靠截取階 階次分別為90、260、230及220。由圖3可以看出組合重力場模型GOCO03S/ GECO、GO_CONS_GCF_2_DIR_R5/GECO、GO_CONS_GCF_2_SPW_R2/GECO及GO_CONS_GCF_2_TIM_R5/GECO的可靠截取階次分別為90、260、220及230。由圖4可以看出組合重力場模型GOCO03S/ EIGEN-6C4、GO_CONS_GCF_2_DIR_R5/ EIGEN-6C4、GO_CONS_GCF_2_SPW_R2/ EIGEN-6C4及GO_CONS_GCF_2_TIM_R5/ EIGEN-6C4的可靠截取階次分別為90、260、230及260。

2.3 組合重力場模型的精度分析

利用2.2中得到的組合重力場模型以及EGM2008、GECO及EIGEN-6C4超高階重力場模型計算實測GNSS點位的高程異常值，并與GNSS/水準實測的高程的高程異常值比較，結果見表2—表4，由表2—表4得到的重力場模型精度結果見圖5。

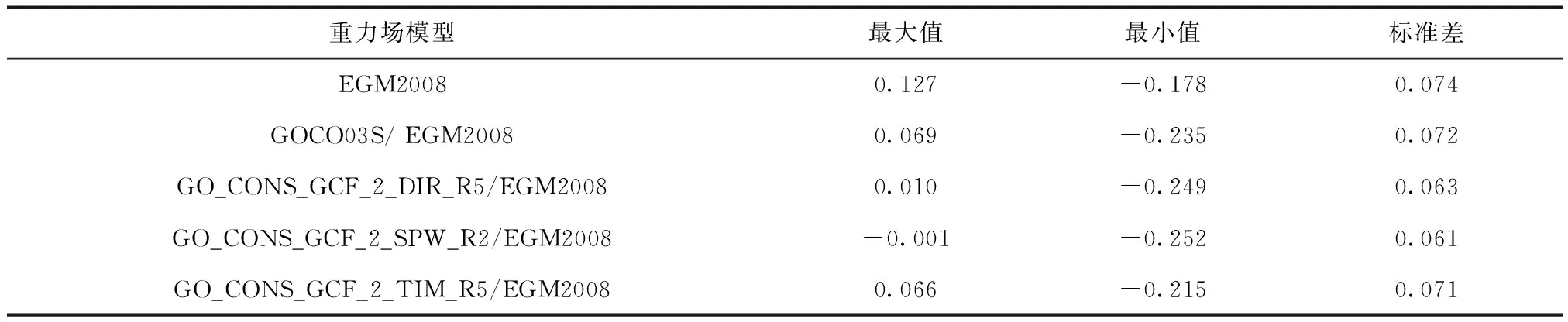
表2 EGM2008及其對應的組合重力場模型與實測高程異常比較結果 m

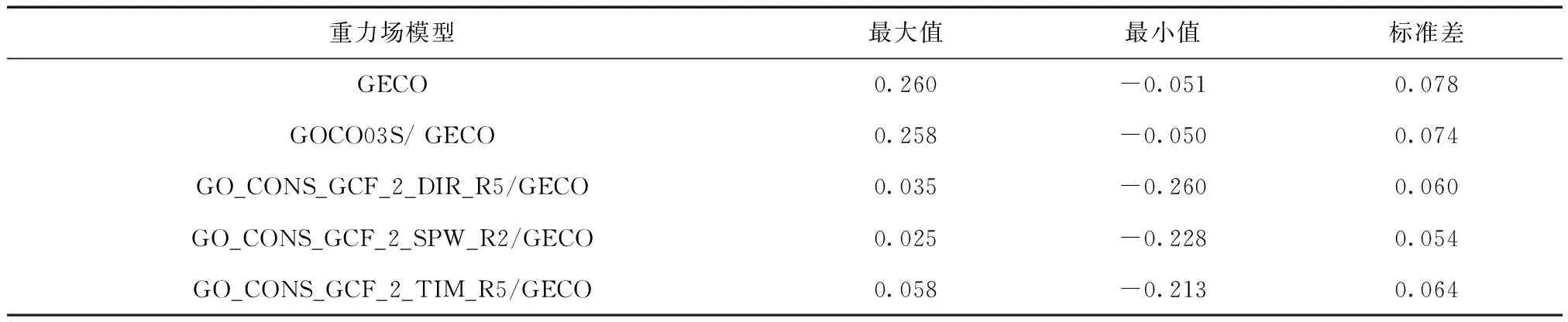
表3 GECO及其對應的組合重力場模型與實測高程異常比較結果 m

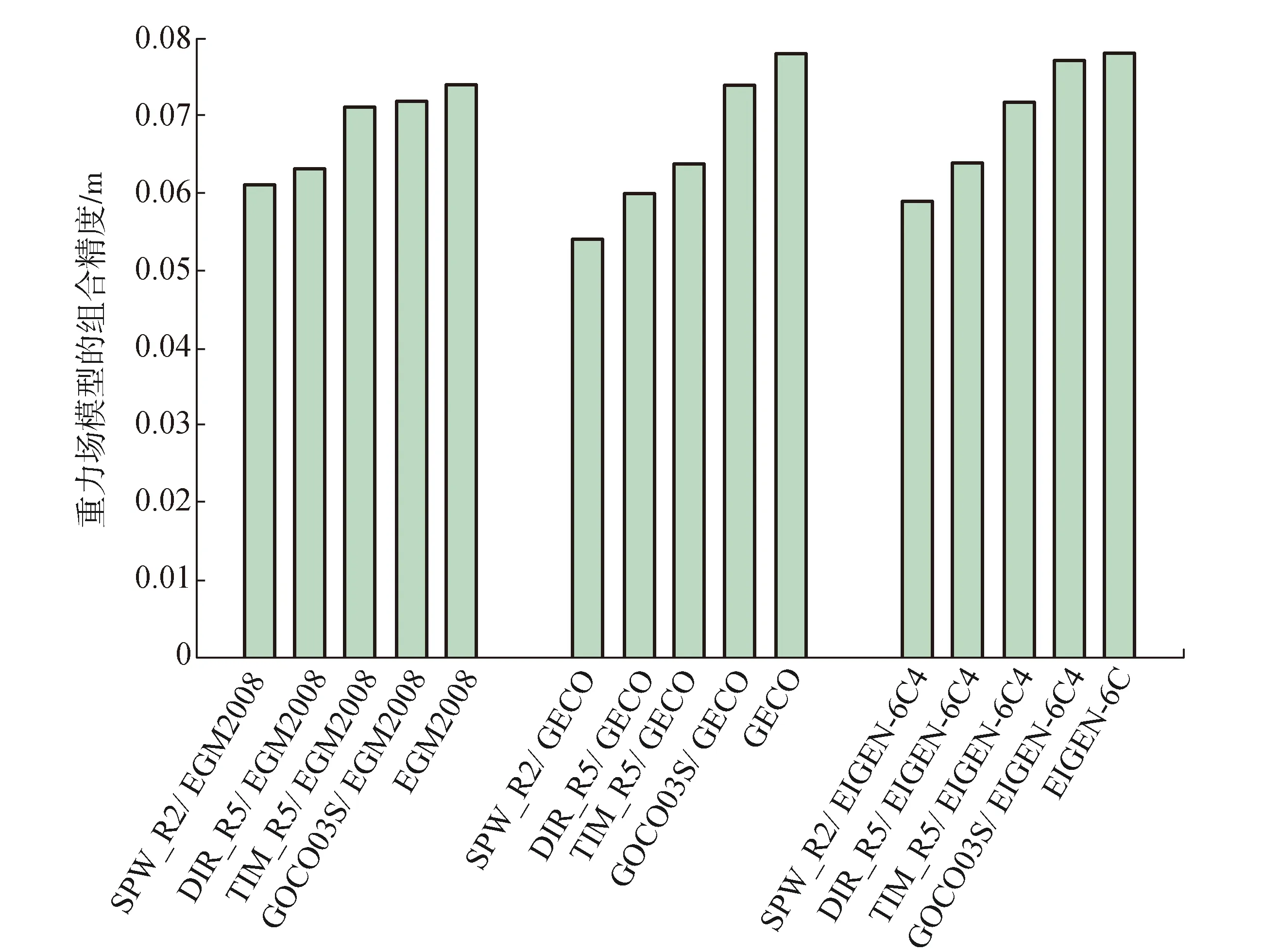
圖5 重力場模型精度結果

由表2可以看出：在實驗區域，EGM2008對應的組合重力場模型精度最優為0.061，最差為0.072，而EGM2008的精度為0.074，因此高程異常的精度最高提升18%；組合重力場模型的精度比EGM2008的精度都要高，見圖5。

由表3可以看出：在實驗區域，GECO對應的組合重力場模型精度最優為0.054，最差為0.074；而GECO的精度為0.078，因此高程異常的精度最高提升31%；組合重力場模型的精度比GECO的精度都要高，見圖5。

由表4可以看出：在實驗區域，EIGEN-6C4對應的組合重力場模型精度最優為0.059，最差為0.077；而EIGEN-6C4的精度為0.078。因此高程異常的精度最高提升24%；組合重力場模型的精度比EIGEN-6C4的精度都要高，見圖5。

綜合表2、表3、表4及圖5可以看出：4種純衛星重力場模型截取可靠階次后對EGM2008、GECO及EIGEN-6C4模型精度提升能力從大到小以此為GO_CONS_GCF_2_SPW_R2、

GO_CONS_GCF_2_DIR_R5、GO_CONS_GCF_2_TIM_R5、GOCO03S。GO_CONS_GCF_2_SPW_R2

對于精度提高影響最明顯，GOCO03S對于精度提高影響最小。

2.4 組合重力場模型在GNSS高程擬合中的應用

根據圖1的選點方案，其中40個點為擬合點，13個點為檢核點。利用2.3中得到的精度最高的組合模型(GO_CONS_GCF_2_ SPW_R2/EGM2008、GO_CONS_GCF_2_SPW_R2/GECO、GO_CONS_GCF_2_SPW_R2/ EIGEN-6C4)以及高階重力場模型(EGM2008、GECO、EIGEN-6C4)，基于1.3中的原理，采用多面函數擬合法進行GNSS高程擬合，檢核點與GNSS/水準比較結果見表5。

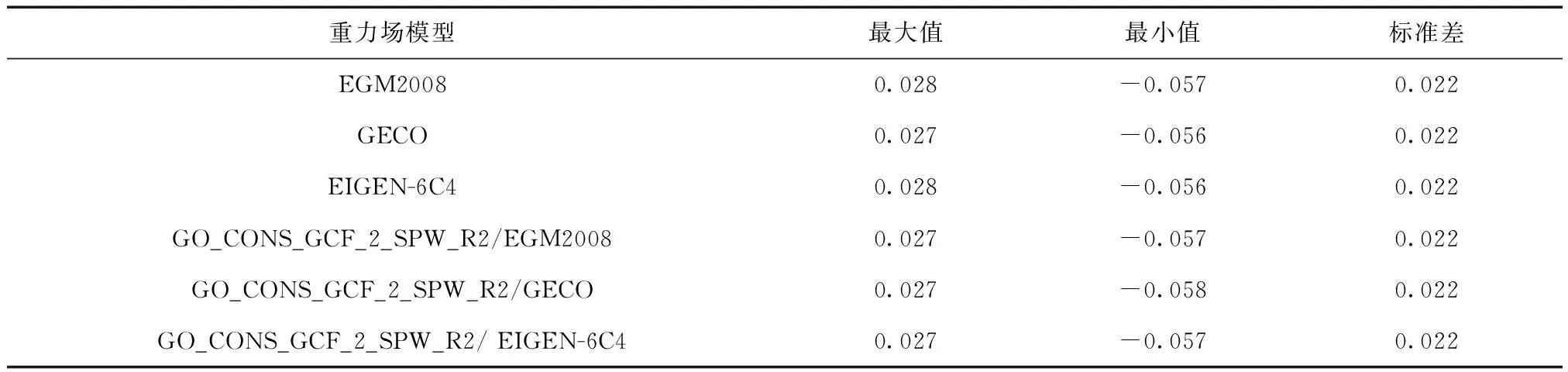
表5 檢核點與GNSS/水準比較結果 m

從表5可以看出，利用EGM2008、GECO及EIGEN-6C4超高階重力場模型進行高程擬合的精度與利用組合重力場模型進行高程擬合的精度相當，這說明EGM2008、GECO及EIGEN-6C4超高階重力場模型存在的長波段誤差也可通過一定的擬合模型進行削弱。

3 結束語

本文進行了組合重力場模型的精度及其適用性分析，得出以下結論：

1)在本實驗區域，GNSS/水準數據檢核表明， EGM2008、GECO及EIGEN-6C4超高階重力場模型的精度都達到厘米級，且EGM2008重力場模型的精度稍高于GOCE和EIGEN-6C4模型的精度。

2)利用GNSS/水準數據檢核組合重力場模型表明，組合重力場模型能提高重力場模型精度。EGM2008對應的組合重力場模型精度比EGM2008精度至少提高3%，最優提高18%。GECO對應的組合重力場模型精度比GECO精度至少提高5%，最優提高31%。EIGEN-6C4對應的組合重力場模型精度比EIGEN-6C4精度至少提高2%，最優提高24%。

3)4種純衛星重力場模型截取可靠階次后對EGM2008、GECO及EIGEN-6C4精度提升能力影響最大的是GO_CONS_GCF_2_SPW_R2，影響最小的是GOCO03S。

4)利用EGM2008、GECO及EIGEN-6C4超高階重力場模型進行高程擬合的精度與利用組合重力場模型進行高程擬合的精度相當，這說明EGM2008、GECO及EIGEN-6C4超高階重力場模型存在的長波段誤差也可通過一定的擬合模型進行削弱。