鋰電池組高溫節點空氣冷卻方案的數值模擬

2018-07-25 02:25:22路昭余小玲張立玉韋立川高松邱亞林金立文孟祥兆

西安交通大學學報 2018年7期

路昭, 余小玲, 張立玉, 韋立川,3, 高松,4, 邱亞林, 金立文, 孟祥兆

(1.西安交通大學能源與動力工程學院, 710049, 西安; 2.西安交通大學人居環境與建筑工程學院, 710049, 西安;3.深圳市英維克科技股份有限公司, 518000, 廣東深圳; 4.中國工程物理研究院材料研究所, 621907, 四川江油;5.云南電力試驗研究院, 650051, 昆明)

鋰離子電池因能量密度高、循環壽命長、自放電率低、工作溫度范圍寬等優點受到了行業的青睞,是目前純電動汽車首選的動力蓄電池[1-2]。作為純電動汽車唯一的動力源,動力鋰離子電池的工作性能直接影響電動汽車的安全、高效運行。影響電池性能的因素主要包括電池材料、結構設計及運行溫度等。對于商業用鋰離子電池而言,目前常關注的是鋰離子電池的運行溫度對電池性能的影響。由于熵變、歐姆內阻及極化內阻的影響,鋰離子電池在充放電過程中均會產生大量的熱量,特別是對于密集布置的動力電池組而言,電池包內部單體電池產生的熱量互相影響、迅速聚集,會導致動力電池組溫度急劇升高。當電池溫度過高時,不僅會加速電池老化、縮短電池使用壽命,嚴重時還會導致電池發生熱失控,進而造成難以估計的安全事故[3-5]。此外,學者們還研究了動力電池組內部溫度均勻性對鋰電池性能的影響,結果表明不均勻的溫度分布會造成動力電池組內部各電池單體不一致的充放電特性,從而導致電池組能量利用不充分及性能衰減[6-7]。根據以上分析,為確保電動汽車安全、高效運行,動力電池組需要在適宜的溫度范圍工作。目前普遍認可的鋰離子電池最佳工作溫度范圍為25～40 ℃[8],因此電池熱管理系統已經成為電動汽車動力電池組安全、高效運行的必要組成部分。

目前,各種形式的電池熱管理系統都得到了廣泛的研究和應用,如空氣熱管理系統、液體熱管理系統及相變儲能熱管理系統[3,6-7,9-11]。由于結構簡單、制造成本低、自消耗能量少等優勢,傳統的空氣熱管理系統目前仍然是大多數電動汽車廠家的首選方案。需要強調的是,精心設計的空氣熱管理系統依然能夠滿足絕大多數電動汽車動力電池組的運行溫度要求[9-11]。Mahamud等通過建立二維數學模型,研究了往復式空氣流對順排布置動力電池組溫度特性的影響規律,結果表明往復式空氣流冷卻方案可以有效降低動力電池組的最高溫度和最大溫差[9]。Wang等采用ANSYS Icepak 14.5商業軟件建立了三維數學模型,用來研究空氣冷卻方案和電池布置方式對動力電池組熱特性的影響[10]。研究者普遍認為,最佳的空氣冷卻方案應該同時考慮冷卻效果、電池組空間利用以及經濟性。本文作者前期對冷卻空氣縱掠密集布置動力電池組進行了相關研究,發現強迫空氣冷卻能夠有效改善動力電池組內部的溫度分布,并且通過綜合考慮冷卻效果和電池組空間利用,獲得了合適的電池間距[11]。

根據以上文獻可知,目前對電動汽車動力電池組空氣熱管理系統已經進行了大量的研究,并且針對影響動力電池組溫度特性的因素,如送風策略、電池組布置方式,提出了相應的優化方案。眾所周知,為確保電池正負極與導電片接觸良好、固定可靠,用單體電池組成動力電池組往往需要大量的電池正負極固定件。然而,目前關于動力電池組的研究往往忽略了電池正負極固定件的影響,其原因一是研究者們普遍認為電池正負極固定件主要只是起滿足電絕緣及固定電池的作用;二是研究者們主要關注電池自身產熱及電池與冷卻介質之間的換熱能力,而忽略了電池正負極固定件的傳熱性能。基于此,本文建立了含電池正負極固定件的動力電池組三維數學模型,研究了送風速度、固定件熱導率對動力電池組溫度特性的影響規律,獲得了滿足電池正負極固定件絕緣性能的最優熱導率,并且基于電池正負極固定件最優熱導率,采用導熱翅片改善了動力電池組內部的溫度均勻性。

1 物理模型

圖1為動力電池組錯列布置示意圖,該動力電池模組主要由Sanyo18650鋰離子單體電池和環氧樹脂電池正負極固定件組成。單體電池直徑D=18 mm,長度L=65 mm,環氧樹脂固定件厚度δt=18 mm,電池組縱向節距比Pl/D=1,橫向節距比Pt/D=1.1,環氧樹脂固定件的中心距Fp=65 mm。

由圖1可知,單體電池在x-y平面周期性錯列布置并聯連接,沿z方向周期性布置串聯連接。因此,本文選取2個相鄰固定件之間的電池單元進行研究。計算區域、固定件及固定件處的翅片如圖2所示。

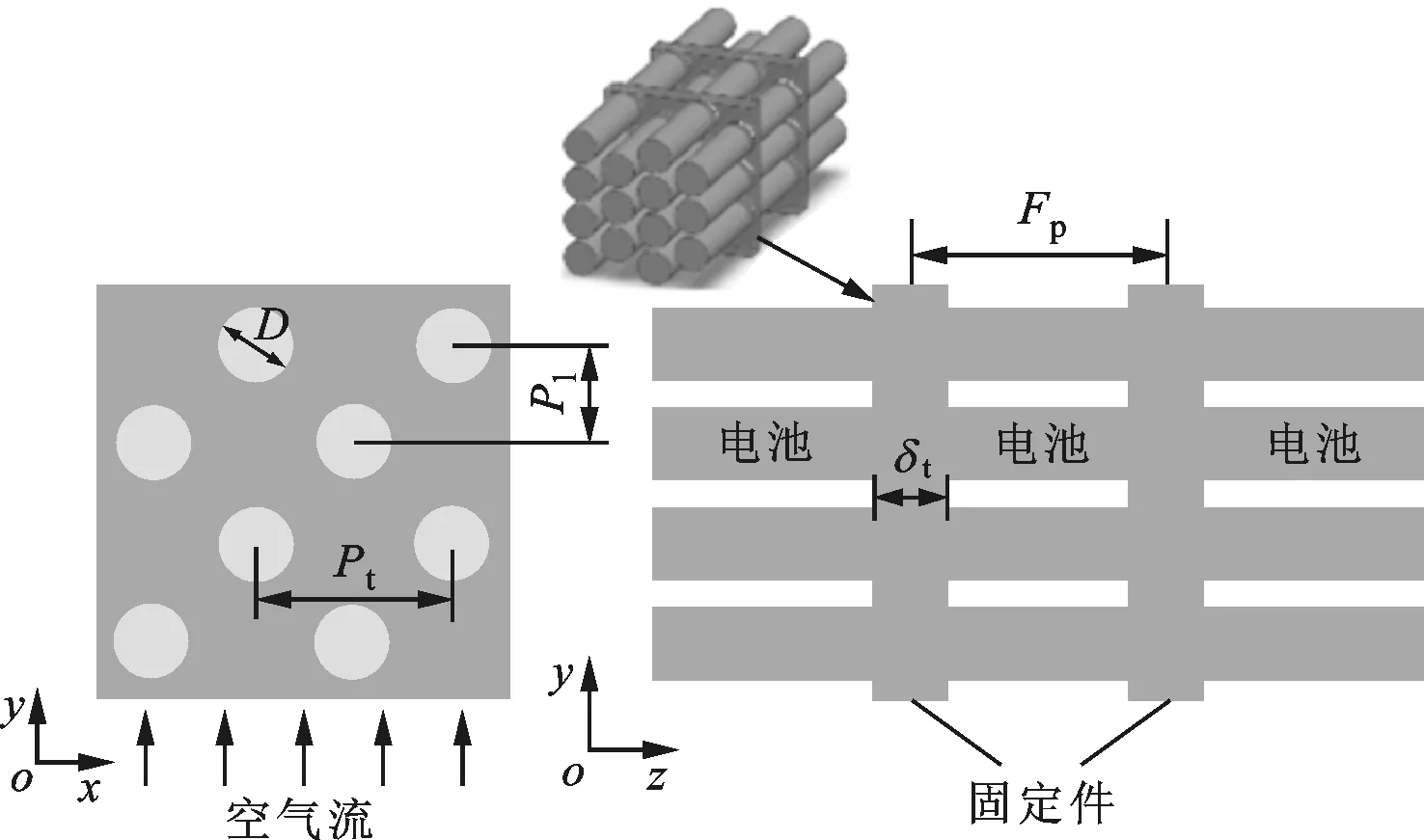
圖1 動力電池組錯列布置示意圖

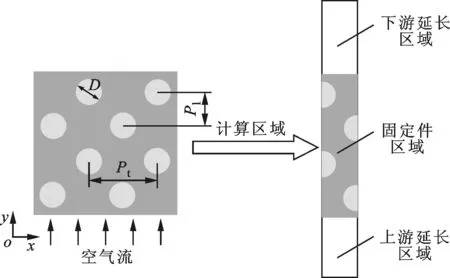
(a)計算區域二維示意圖

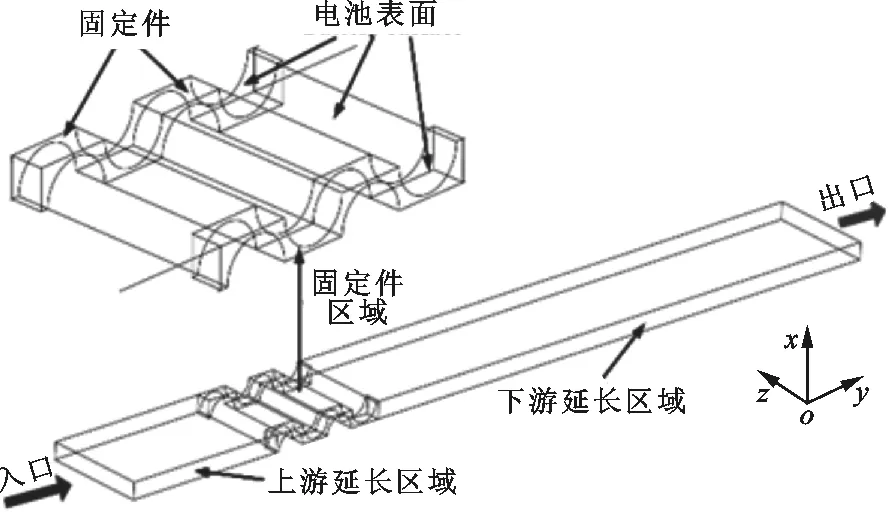
(b)含有固定件的計算區域三維示意圖

(c)含有翅片的計算區域局部示意圖圖2 系統計算區域及含固定件和固定件處翅片的計算區域示意圖

為減小固定件厚度對計算區域入口空氣速度分布的影響,將計算區域入口延長1.5倍,同時為確保冷卻空氣單向均勻流出計算區域,將計算區域出口延長5倍,此方法已經被廣泛應用于翅片管換熱器的相關研究[12-13]。因此,整個計算區域沿流動方向的長度是實際固定件區域長度的7.5倍。為進一步改善固定件的散熱情況,在相鄰2個固定件之間布置一定數量的導熱翅片,導熱翅片尺寸為0.5 mm(x)×0.5 mm(y)×47 mm(z)。

2 數學模型

2.1 控制方程及基本假設

盡管電池瞬態產熱模型能夠準確地預測電池的瞬時產熱量,但是瞬態產熱模型往往需要消耗大量的計算時間。同時,考慮到電池正負極固定件對動力電池組散熱性能的影響,空氣橫掠動力電池組內部的換熱問題不僅包括冷卻空氣與電池表面、固定件表面及翅片表面的強迫對流換熱,還包括固定件及翅片內部的導熱,因此對于動力電池組而言,這種復雜的瞬態耦合換熱問題在求解時間上缺乏可行性。本文的目的是揭示電池正負極固定件對動力電池組換熱與流動性能的影響規律,因此,采用平均面熱源模擬電池發熱量以減少數值計算時間,這種簡化方法目前常用于動力電池組的熱管理研究[11,14]。

考慮到動力電池組內部空氣流速較小,溫度變化不大,因此假定冷卻空氣為不可壓縮流體、常物性、層流流動。此外,由于實際應用中常采用導熱性能優良的導熱硅膠填充于固定件與電池表面之間狹小的縫隙處以確保兩者緊密接觸,減小接觸熱阻對動力電池組內部熱環境的影響,因此本文忽略了固定件與電池表面之間的接觸熱阻。采用商業軟件ANSYS14.5研究空氣橫掠錯列布置電池組內部的流動與換熱問題,描述計算區域內部冷卻空氣換熱與流動問題的控制方程主要包括:

連續性方程

(1)

動量方程

(2)

能量方程

(3)

當流體速度為零時,固定件及翅片區域的能量方程可簡化為

(4)

以上各式中:u為流體速度,m·s-1;ρ為密度,kg·m-3;μ為動力黏度,Pa·s;cp為比定壓熱容,J·kg-1·K-1;λ為熱導率,W·m-1·K-1;j為笛卡爾坐標。

2.2 邊界條件

冷卻空氣進口采用速度入口邊界條件,并假設同一送風口的所有位置送風速度和送風溫度為相同的值;出口采用自由流出邊界條件,即所有的空氣都單向均勻流出;電池表面采用恒定熱流密度邊界條件,q=24.4 W·m-2,該值通過電池平均發熱量與電池有效傳熱面積之比求得;固定件與電池和冷卻空氣的接觸面均為耦合邊界條件。

2.3 數值方法

首先采用前處理軟件Gambit 2.4.6建立動力電池組的物理模型,然后用結構化網格(四邊形和六面體網格)對空間進行網格劃分,并在電池表面、翅片表面、送回風口附近采用適當的網格加密。經過網格數獨立性測試驗證,數值計算時選取的網格數為723 190。采用二階迎風格式對控制方程進行離散化,并選用SIMPLE算法對離散方程進行求解。

3 結果與討論

3.1 模型驗證

目前尚未見到研究電池正負極固定件對動力電池組散熱性能的影響的相關報道,無法直接用前人的相關數據來驗證本文所建立的數學模型,所以采用文獻[15]中的方法,即采用冷卻空氣橫掠翅片管的相關數據進行驗證。數學模型驗證的相關參數如下:管外徑為18 mm,管壁溫度為37.7 ℃,管束入口冷卻空氣溫度為16 ℃,入口空氣流速變化范圍為0.67～4 m·s-1。一般而言,空氣橫掠翅片管束的流動可看成包括2種流動:一種是空氣在相鄰2個翅片間的管內流動,此時翅片管束內空氣的雷諾數變化范圍為333～2 000(<2 300),屬于層流流動;另一種是空氣橫掠管束的流動,此時翅片管束內空氣的雷諾數變化范圍為1 000～6 000,也屬于層流流動(<1.4×105)。因此,在數學模型驗證時采用層流模型進行研究。圖3給出了努塞爾數隨雷諾數的變化規律,可以發現本文數學模型的計算結果與文獻[12]的實驗結果相近,最大偏差小于5%,由此說明,本文所建立的數學模型和數值方法可用于研究電池正負極固定件對動力電池組熱特性與流動特性的影響規律。

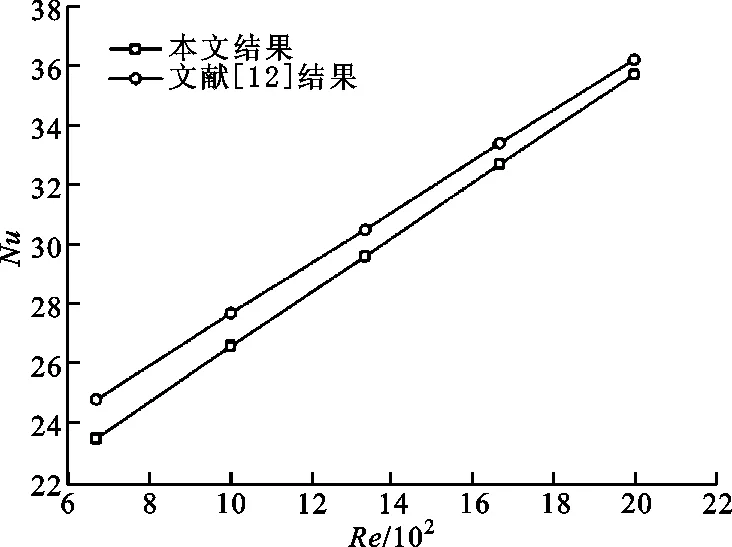
圖3 努塞爾數隨雷諾數的變化規律

3.2 電池正負極固定件的影響

為了揭示電池正負極固定件對動力電池組內部溫度的影響,首先研究了無固定件時動力電池組內部的溫度情況,將其稱為算例1;其次研究了絕緣性能優良、導熱性能較差的環氧樹脂作為傳統電池正負極固定件對動力電池組內部溫度的影響,將其稱為算例2;最后根據上述研究結果,研究了不同固定件的熱導率對動力電池組內部溫度的影響,獲得了滿足電池正負極固定件絕緣性能的最佳熱導率,將其稱為算例3。

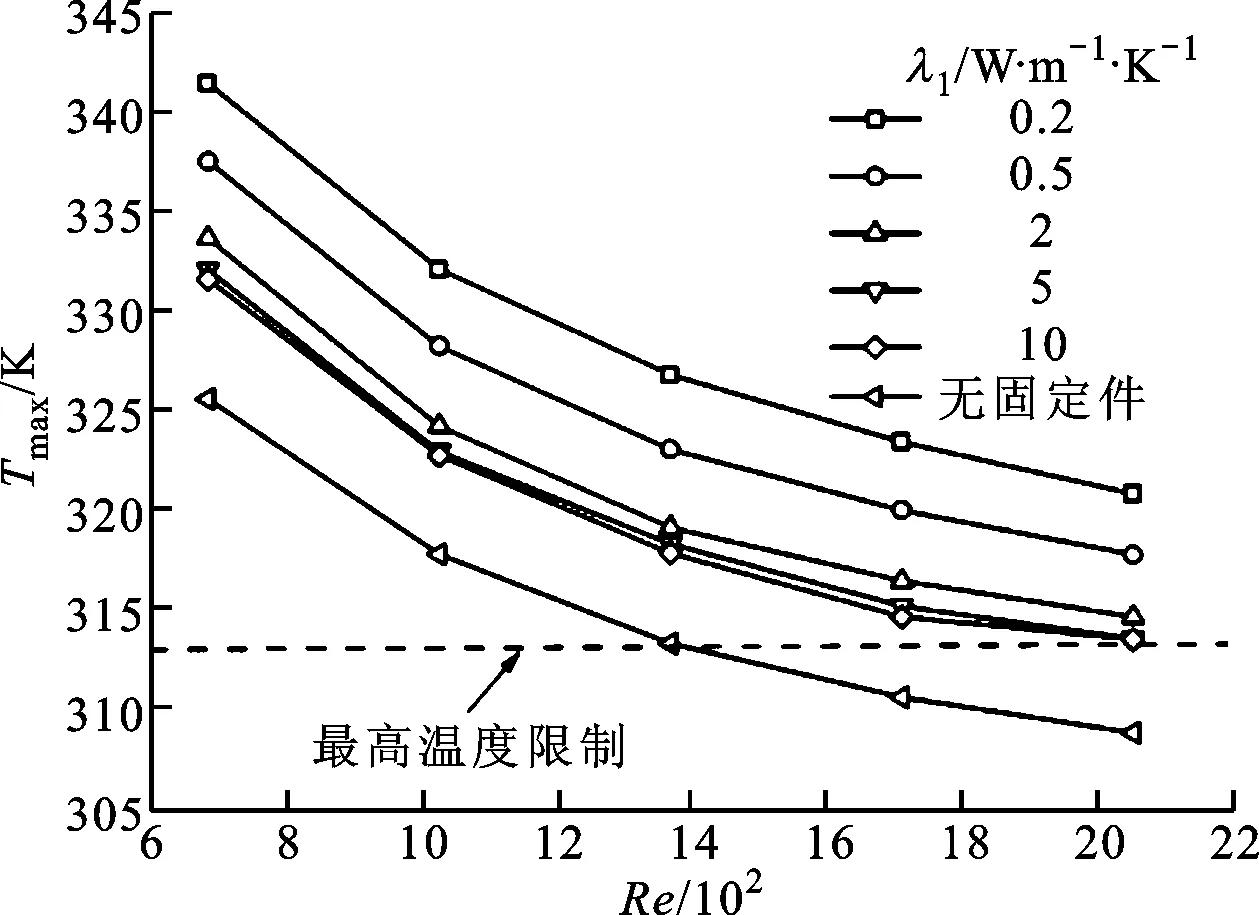
電池正負極固定件對動力電池組內部最高溫度的影響如圖4所示,從中可以發現,在所研究的雷諾數范圍內,未考慮固定件的動力電池組內部最高溫度顯著低于傳統環氧樹脂(λ1=0.2 W·m-1·K-1)作為固定件時的最高溫度。例如:當Re=2 052時,前2種算例的動力電池組內部最高溫度相差約12 K;當1 3682 W·m-1·K-1時,固定件熱導率對動力電池組內部最高溫度的影響顯著減小,說明當冷卻空氣在錯列布置的動力電池組內部處于層流流動時,可使動力電池組整體的散熱性能達到最優的固定件熱導率為2 W·m-1·K-1,這主要是因為當固定件熱導率大于2 W·m-1·K-1時,導熱熱阻在總傳熱熱阻中的比重顯著減小,即固定件熱導率對動力電池組整體散熱性能的貢獻明顯降低。此外必須注意的是,固定件首先必須確保動力電池組的電絕緣性能,其次才是滿足動力電池組的散熱需求。目前,環氧樹脂基氧化鋁復合材料因兼具優良的絕緣性能和較好的導熱性能而得到了普遍關注,常用于絕緣、散熱性能要求較高的電子產品冷卻中。經文獻調研得知,當熱導率為2 W·m-1·K-1時,環氧樹脂基氧化鋁復合材料具有優良的絕緣性能[16],由此說明本文在一定的雷諾數范圍內所得到的動力電池組正負極固定件的最優熱導率(2 W·m-1·K-1)具有實際工程意義。

圖4 固定件熱導率對動力電池組最高溫度的影響

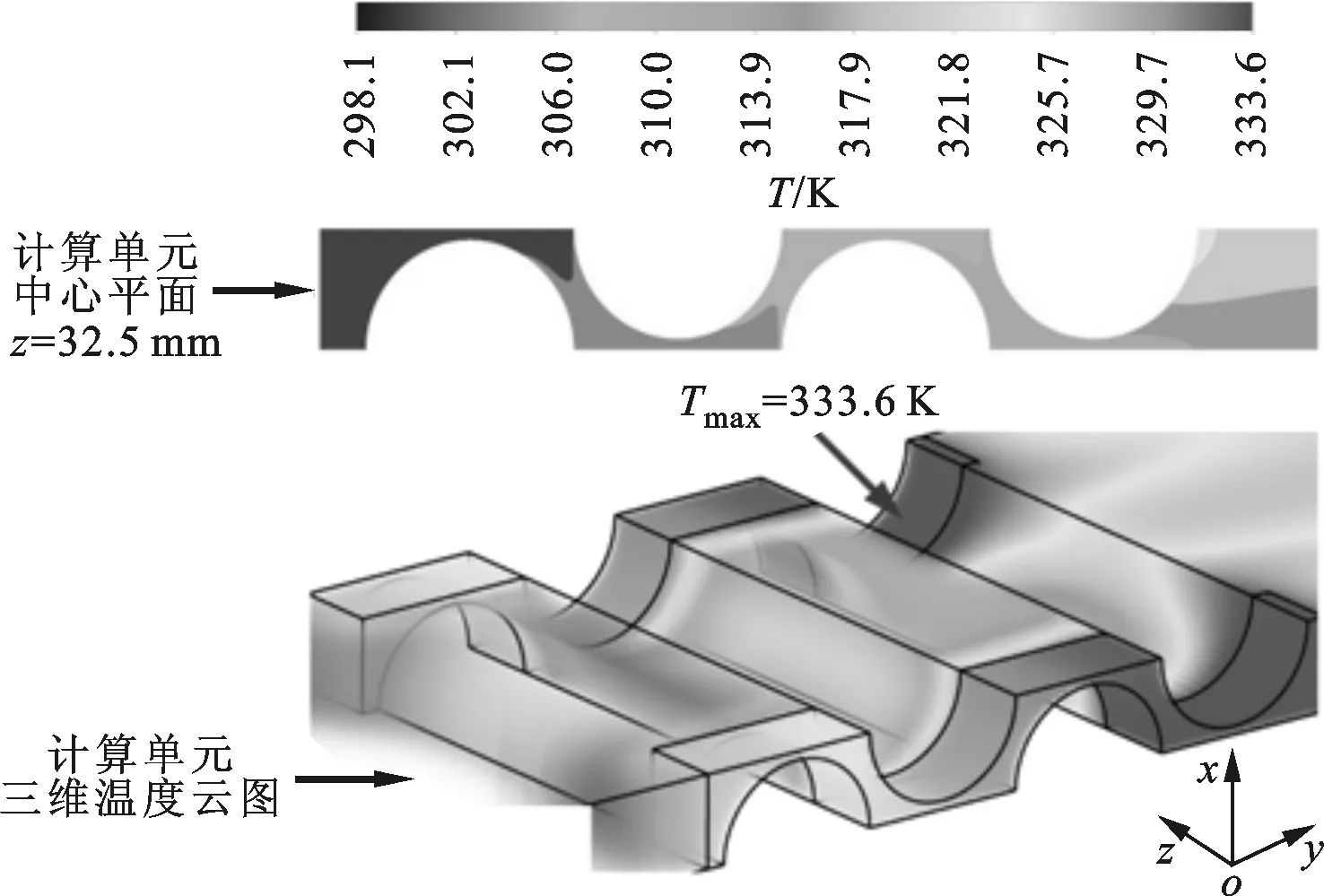
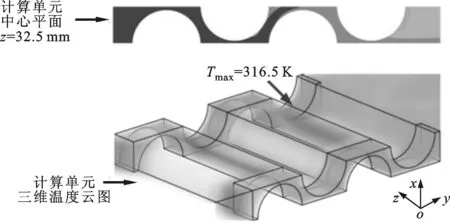
圖5為動力電池組在最優熱導率、不同雷諾數下的溫度云圖。從計算單元的三維溫度云圖可知,動力電池組的高溫區域均出現在沿冷卻空氣流動方向下游側的固定件處,固定件之間的區域溫度明顯較低。此外,從計算單元中心截面z=32.5 mm處的溫度云圖可知,與冷卻空氣直接接觸的電池表面的最高溫度明顯低于動力電池組的最高溫度。例如,當Re=2 052時,動力電池組的最高溫度約為314.7 K,而與冷卻空氣直接接觸的電池表面的最高溫度約為308.5 K,兩者相差6.2 K。上述結果主要由以下3個原因所導致:一是雖然采用了具有最佳熱導率的固定件,但是由于其自身導熱熱阻的影響,依然增大了固定件處電池表面與冷卻空氣的傳熱熱阻;二是固定件之間的電池表面與冷卻空氣間僅存在對流傳熱熱阻;三是冷卻空氣沿流動方向不斷帶走動力電池組產生的熱量,因此空氣流溫度逐漸升高,導致下游側空氣換熱能力下降。

由圖5e可以看出,當Re=2 052時,采用最優熱導率的動力電池組內部最高溫度為314.7 K,最大溫差ΔTmax=14.9 K,均超過了動力鋰離子電池組的最高溫度限制(313.15 K)和最大溫差限制(10 K)。因此,為了確保動力鋰離子電池組在適宜的溫度范圍內運行,需要進一步強化動力電池組的空氣冷卻能力。

3.3 電池正負極固定件處翅片的影響

(a)Re=684

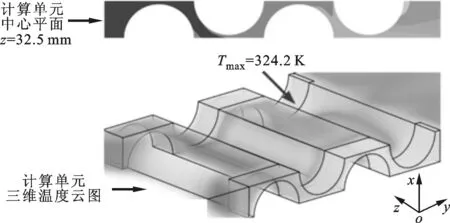
(b)Re=1 026

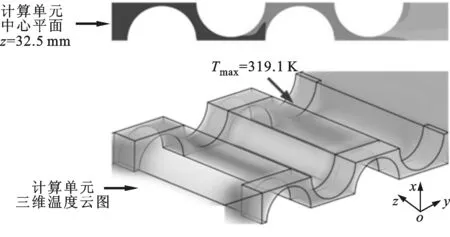
(c)Re=1 368

(d)Re=1 710

(e)Re=2 052圖5 不同雷諾數下動力電池組計算單元的溫度云圖(λ1=2 W·m-1·K-1)

由3.2節可知,采用最優熱導率的動力電池組具有優良的散熱性能,然而在所研究的雷諾數范圍內,動力電池組內部的熱環境依然不能滿足鋰離子電池的溫度要求。根據牛頓冷卻公式可知,當電池產熱量、冷卻空氣送風溫度一定時,減小冷卻空氣與電池表面之間的傳熱熱阻可以有效減小電池表面與冷卻空氣之間的傳熱溫差,即可以降低動力電池組的整體溫度。為此,在相連的2個固定件之間布置成組的導熱翅片,以減小冷卻空氣與固定件之間的傳熱熱阻。同時,為了研究導熱翅片數量、位置、熱導率對動力電池組內部溫度的影響,采用2種方案在固定件之間布置導熱翅片:方案一是沿冷卻空氣流動方向在相鄰2個電池單元之間均勻布置3個導熱翅片,由于本文研究的動力電池組計算單元沿流動方向由4排電池單元組成,因此方案一沿冷卻空氣流動方向均勻布置9個導熱翅片,如圖2c所示;方案二是沿冷卻空氣流動方向在最后2排電池之間布置3個導熱翅片。

圖6給出了冷卻空氣雷諾數為2 052、固定件為最優熱導率(2 W·m-1·K-1)時,動力電池組內部最高溫度隨導熱翅片熱導率的變化規律。

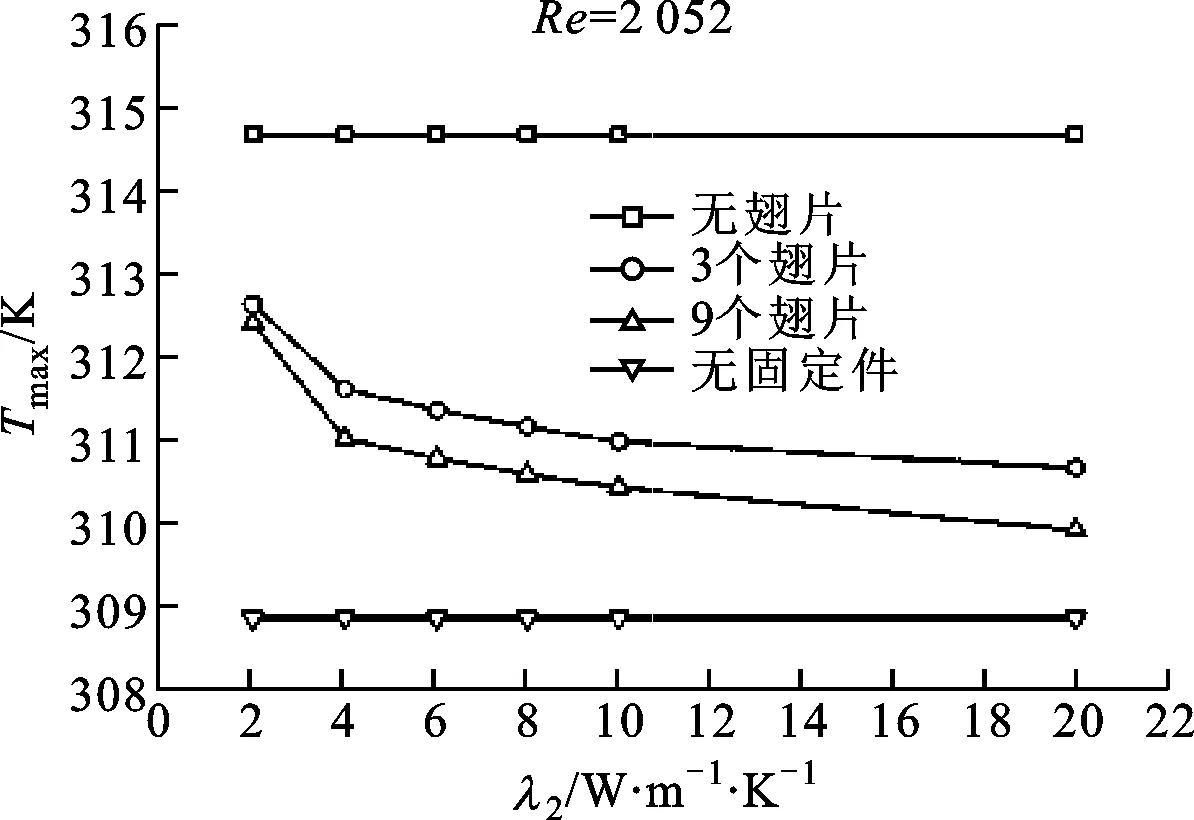
圖6 導熱翅片熱導率對最高溫度的影響

圖6中最上面的直線為固定件之間沒有布置導熱翅片時動力電池組的最高溫度,將其稱為無翅片算例;最下面的直線為無固定件時動力電池組的最高溫度,將其稱為無固定件算例。在這2個算例中,動力電池組內部最高溫度與導熱翅片熱導率無關,以下將其與增加導熱翅片后的算例進行對比。由圖6可知,當導熱翅片與固定件的熱導率均為2 W·m-1·K-1時,無論采用方案一或者方案二,動力電池組內部的最高溫度均明顯低于無翅片算例動力電池組內部的最高溫度,相差約2 K。此外,隨著導熱翅片熱導率逐漸增加,方案一的冷卻效果稍優于方案二的冷卻效果,2種方案的動力電池組內部最高溫度相差約0.7 K。值得注意的是,2種方案的動力電池組內部最高溫度的下降幅度均逐漸減小。例如對于方案一而言,當導熱翅片的熱導率從2 W·m-1·K-1增加到4 W·m-1·K-1時,動力電池組內部的最高溫度下降約1.5 K,而當導熱翅片的熱導率從4 W·m-1·K-1增加到20 W·m-1·K-1時,動力電池組內部的最高溫度下降約1 K,主要原因是隨著導熱翅片熱導率的逐漸增大,導熱熱阻在總傳熱熱阻中的比重逐漸減小,而對流傳熱熱阻的比重逐漸增加,因此導熱翅片的熱導率對動力電池組整體散熱性能的貢獻逐漸減小。

冷卻空氣流過動力電池組需要消耗的風機能量由下式計算

P=pdQV

(5)

式中:pd為冷卻空氣的進出口壓降,Pa;QV為冷卻空氣的體積流量,m3·s-1。

圖7為不同雷諾數下電池正負極固定件、導熱翅片數量對冷卻空氣流過動力電池組需要消耗的風機能量的影響,從中可以看出,隨著雷諾數逐漸增大,考慮固定件及導熱翅片的風機能耗明顯高于無固定件算例的風機能耗。例如,當Re=2 052時,方案一的風機能耗是無固定件算例風機能耗的1.8倍。此外,方案一和方案二的風機能耗與無翅片算例的風機能耗差異不大。特別是在所研究的整個雷諾數范圍內,方案二的風機能耗與無翅片算例的風機能耗基本相同。

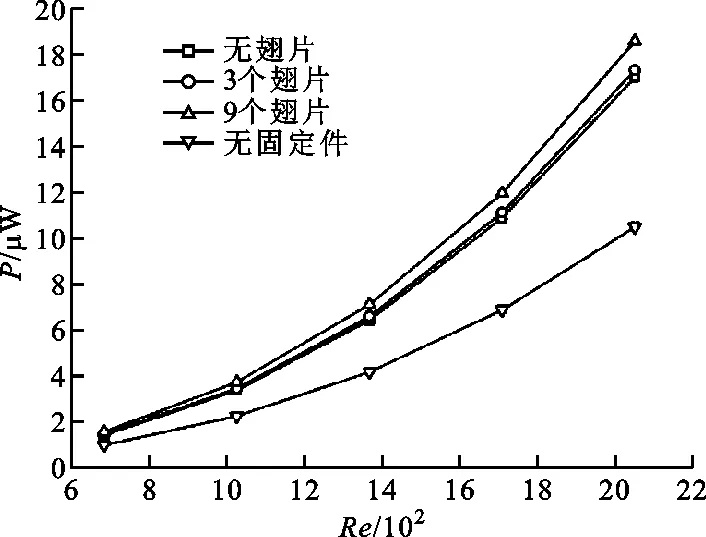
圖7 不同雷諾數下固定件、翅片數量對風機能耗的影響

綜上所述,固定件之間布置導熱翅片可以顯著提高動力電池組的整體散熱性能,確保動力電池組內部最高溫度低于鋰離子電池的最高溫度限制(313.15 K)。此外,動力電池組能否高效運行也與動力電池組內部溫度的均勻性密切相關。因此,為了進一步獲得導熱翅片對動力電池內部溫度均勻性的影響,計算出了冷卻空氣雷諾數為2 052、導熱翅片熱導率為20 W·m-1·K-1時動力電池組的溫度云圖,如圖8所示。

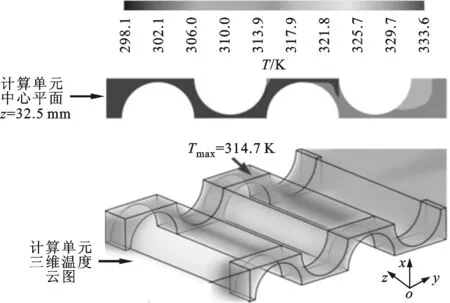
(a)無翅片算例

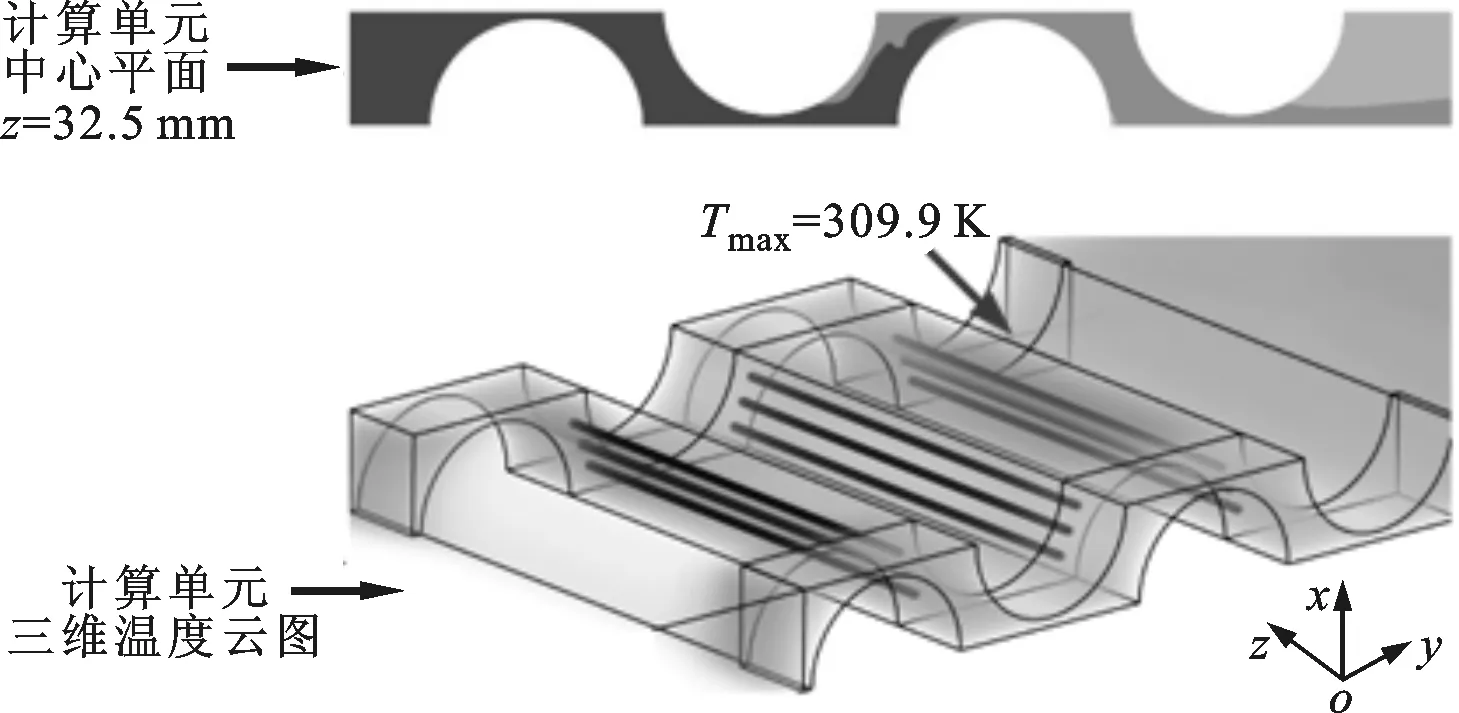
(b)方案一

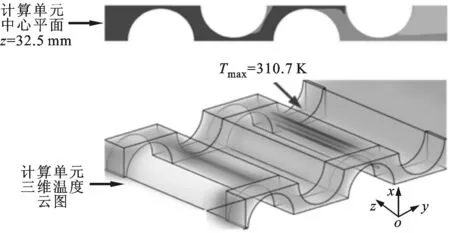
(c)方案二圖8 動力電池組的溫度云圖(Re=2 052,固定件熱導率λ1=2 W·m-1·K-1,翅片熱導率λ2=20 W·m-1·K-1)

由圖8可以看出:相對無翅片算例而言,方案一和方案二的動力電池組內部溫度分布均勻,固定件處并沒有出現明顯的高溫區域。此外,方案一和方案二的動力電池組內部最大溫差分別為9.6 K和10.5 K,明顯低于無翅片算例的動力電池組內部最大溫差14.9 K。上述結果表明,固定件處增加導熱翅片能有效強化動力電池組內部的空氣換熱能力,使得高溫區域的溫度顯著降低,從而減小了動力電池組內部各單體電池之間的溫度差,有利于各單體電池實現一致的充放電特性,確保動力電池組安全、高效運行。