基于可重構度的在軌衛星多級健康評估方法

陸 崢, 金 光, 楊天社, 吳 冠, 蘭新章

(1. 國防科技大學信息系統與管理學院, 湖南 長沙 410073; 2. 中國西安衛星測控中心, 陜西 西安 710043; 3. 復雜航空系統仿真重點實驗室, 北京 100076)

0 引 言

隨著我國衛星數量的逐年增多以及衛星系統的更新換代,現有的在軌衛星監測系統已經無法適應高密度和高可靠性衛星系統狀態監控任務的需求。因此,在軌衛星的多級健康狀態評估技術對航天器的健康管理具有重要意義。文獻[1-5]介紹了集成的航天器健康管理架構(integrated vehicle health management, IVHM)完整組成,本文的健康評估屬于其中的一個重要環節,主要研究利用衛星遙測參數和基于衛星可重構性研究的多級健康狀態評估方法,評估結果以定量形式給出,文獻[6]以健康度量化健康狀態的程度,對于航天器的健康管理具有實用價值。

文獻[7-8]中利用遙測數據挖掘工具Orca和IMS(inductive monitoring system)用于航天器任務執行系統和國際空間站的健康監測,其中,軟件Orca基于k-means算法原理進行健康狀態監測,軟件IMS利用基于聚類的方法提取正常情況下的數據集合,然后計算出實時的數據向量與正常狀態的數據向量之間距離的方差作為特征量進行健康狀態監測。文獻[9]中提出采用神經網絡模型解決評估過程中多參數、多尺度和非齊次性數據,并對國際系統COSPAS-SARSAT進行健康狀態評估。文獻[10]中提出使用有監督的數據挖掘方法,例如決策樹方法、主成分分析方法等,進行飛行器健康狀態的異常檢測,使用無監督的數據挖掘方法,例如k-means算法、正交分割聚類以及一元相關向量機方法,進行飛行器健康狀態的實時監測。這類方法主要是基于數據挖掘的單級健康評估方法,難以體現多級系統中部件對系統健康狀態的影響。

文獻[11]采用Bayes網絡和性能退化方法,利用遙測數據評估JB-3衛星動量輪的在軌健康狀態(失效概率)。文獻[12]提出適用于結構化Bayes網絡模型的、以變化證據信息為導向的、基于Bayes球和交叉熵測度的變模型快速推理算法,實現綜合運載器的健康評估,并以簡化的變速箱健康評估為例進行說明。這類方法主要是基于Bayes網絡的健康評估方法,在評估部件的健康狀態方面相對有效,但是Bayes網絡的建立過程中往往缺乏先驗知識和數據的支持,難以建立完備的Bayes網絡,對于多級的衛星系統而言,應用難度更大,缺乏實用性。

文獻[13]分析衛星控制系統的結構特征,將控制系統進行結構分層并提出了基于層次推理的健康狀態評估方法。文獻[14]提出一種基于多級模糊綜合評價的衛星姿態控制系統的在軌實時健康評估方法。文獻[6]采用非線性模糊變權策略計算健康度的方法進行衛星健康狀態評估。這類方法是基于層次結構的多級健康評估方法,實用性強,但是對于衛星系統的可重構性、高冗余和非線性特性的刻畫不夠。

綜上所述,目前在軌衛星的多級健康狀態評估主要采用加權方法,對衛星系統高冗余、可重構特性的體現不足,且評估模型權重參數的確定過于依賴主觀判斷和專家經驗。例如,加權平均型合成法則沒有體現衛星系統故障重構能力的影響;狀態數法以系統組成部分的特殊關系定義其狀態數時,冗余關系的狀態數需要依靠專家經驗;基于變權的層次分析法在從部件到系統的評估中,部件之間的冗余關系也靠專家經驗給出冗余系數來刻畫。

針對以上問題,本文提出基于可重構度的在軌衛星多級健康狀態評估方法,以可重構度指標刻畫衛星高冗余、可重構和非線性等結構特性對系統健康狀態的影響,首先,采用非參數回歸方法綜合多元參數評估部件級的健康狀態并計算得到部件的健康度;其次,通過對衛星系統的結構與功能分析,建立基于可重構度的系統結構樹模型,在此基礎上進行加權綜合,實現從部件級到系統級的健康狀態評估和健康度計算;最后,通過仿真案例分析對整個評估流程進行方法驗證。

1 部件健康評估

1.1 部件健康狀態特征量的選取

衛星運行狀態指標值由多元狀態估計方法(multivariate state estimation technique,MSET)確定,即表示衛星運行狀態的特征量是由部件到組件到分系統到系統的層次評估過程。由于MSET融合了底層部件的多源數據,反映衛星運行狀態的典型特征量難以形式化表達。在工程實踐領域中,由于考慮到現實因素,常用的選取遙測參數的方法主要依賴于專家意見,領域內專家研究衛星時間久,對表征衛星部件健康狀態的遙測參數較為清楚。因此聽取專家意見可以大大提高評估的有效性和針對性。本文主要根據領域內專家的意見,得出表示衛星部件健康狀況的典型特征量,例如以陀螺儀的測量輸出表示其健康狀態。

衛星部件的健康評估離不開衛星在軌運行產生的遙測參數。通過選取能夠反映衛星部件健康程度的遙測參數進行評估是基本的處理方式。本文用Pi表示某部件的第i個選中的遙測參數,稱為第i個特征參數,特征參數的選取一般由領域內的專家確定,例如對動量輪部件而言,往往選取動量輪轉速、電流和殼溫等作為健康狀態特征量。

需要補充說明的是,在實際應用中,由于遙測參數下行過程中不可避免地受到太空環境、人為操作等因素的干擾,直接將遙測參數輸入到評估流程中可能會造成評估結果的失真,因此,這里的特征參數,往往要經過數據剃野、數據標準化等數據處理過程,進一步地,本文認為特征參數還可以由其他數據處理方法例如統計分析、小波分析、時間序列分析等對遙測參數進行處理后,得到的諸如波動頻率、變化幅度等特征參數來代替,但要盡可能地滿足有效性和獨立性要求。

1.2 基于非參數回歸方法的健康度計算

在進行衛星部件健康狀態評估之前,為了提高評估結果的準確性,使用Tukey提出的53H法進行遙測參數數據孤立野點的剔除。

本文采用非參數回歸方法,根據特定時刻的部件健康狀態特征量,計算對應時刻的部件健康度。采用這種方法的主要依據,一方面在于領域內專家的認可,另一方面在于通過特征量的變化刻畫部件健康度是工程領域的常用做法。

考慮到該方法對于健康評估結果的可信度的存在影響,通過調整系數的值提高可信度。從短期看,由于計算的健康度時變性,健康度必然存在波動性,可信度受損。從長期影響看,經過預處理過的遙測數據能表現出衛星各部件的數據本質。因此,數據波動性對可信度的影響是有限的,可通過調整系數降低波動性,提高可信度,使得健康度的評估結果符合實際。

設某部件有n個健康狀態特征參數P1,P2,…,Pn,基于非參數回歸的部件健康狀態評估步驟如下:

步驟1根據設計或歷史數據獲取典型健康狀態(典型健康狀態不必包含所有的健康狀態)下部件特征量的最大值和最小值。記第i個特征參數Pi的最大值和最小值為mini和maxi。

步驟2獲取典型健康狀態下部件健康狀態特征量數據矩陣T。設共包含了K個時間,將T表示為n×K矩陣形式為

(1)

稱T為健康狀態矩陣,T包含各特征參數取極值(包括其極大值和極小值)時刻的數據。采用標準化的健康態數據,標準化的特征量數據為

(2)

標準化后的健康狀態數據矩陣仍記為T。

步驟3獲取特定時刻部件健康狀態特征量數據Pobs=(p1,p2,…,pn)T,這里pi表示特征參數Pi的觀測值。

步驟4采用同樣的方式標準化觀測數據,標準化的特征量數據為

得標準化的觀測數據向量為Zobs=(z1,z2,…,zn)T。

步驟5根據觀測向量Zobs和健康狀態特征量數據矩陣T,計算部件偏離健康狀態的程度為

Θ=‖[T·(TT·T+αIK)-1TT-In]·Zobs‖

(3)

式中,‖·‖表示向量的歐幾里得范數；α是正則化系數。

步驟6計算部件健康狀態指標H。取偏離健康狀態的程度Θ的生存函數值作為部件健康程度的量化,也就是健康度H,即

(4)

2 系統健康評估

2.1 衛星系統結構樹建模方法

本文提出建立衛星系統結構樹進行系統的健康評估方法,將衛星的零部件、組件、分系統等系統元素按照一定的層次關系組織起來,并根據功能要求對系統元素的工作邏輯進行描述的樹狀結構。樹上的節點代表各層次的系統元素,其中葉節點表示無需再分的系統元素,非葉節點是由其子節點構成的系統元素,根結點表示整個系統。

系統元素之間的工作邏輯是指非葉節點完成設計功能時,其子節點對應的系統元素集合的功能和工作邏輯關系應滿足的要求。衛星系統結構樹采用串聯、并聯和冗余3種工作邏輯。設某非葉節點為s,其子節點為e1,e2,…,em,即系統元素e1,e2,…,em構成更高層次的系統元素s,e1,e2,…,em為s的構成元素,要求e1,e2,…,em是相互獨立的。e1,e2,…,em的工作邏輯表示為完成s的規定功能,對e1,e2,…,em完成其規定功能的要求。可定義幾種典型的工作邏輯。

(1)串聯。s完成其功能需要e1,e2,…,em全部完成其功能;

(2)并聯。s完成其功能只要e1,e2,…,em中至少一個完成其功能;

(3)Ω-冗余。設Ω是{e1,e2,…,em}的冪集的不包含空集的一個真子集,s完成其功能的必要條件是存在ω∈Ω,ω內所有部件完成其功能。

2.2 衛星系統的可重構性定義和可重構度計算

2.2.1 衛星系統的可重構性定義

本文借鑒了計算機領域和制造領域的可重構性概念[14-18],結合衛星系統的高冗余和高可靠性設計,得出衛星系統也是可重構性系統這一結論,這種特性應當給予定性和定量地分析。

定義1衛星系統的可重構性是指衛星系統的組成元素發生故障后,通過主動或者被動容錯控制策略,使得衛星系統仍然可以執行其功能的特性,是對衛星系統高冗余和高可靠性設計的綜合體現。

2.2.2 衛星系統可重構度的計算

考慮到可重構性是基于衛星系統結構樹(或衛星系統)衍生的特性,因此,具體到計算層次而言,本文的可重構度由定義2給出。

定義2可重構度是對衛星系統可重構性的度量。衛星系統結構樹中系統元素s的可重構度,是其構成元素故障后,通過主動或者被動容錯控制策略配置其構成元素,使得該系統元素s仍然可以執行其功能的能力的度量。需要特別指出,對于系統結構樹中最底層的沒有構成元素的系統元素,其可重構度為0。

根據系統結構和功能,以及所確定的系統各層次組成元素的邏輯關系,逐層確定系統結構樹中各系統元素的可重構度。

當系統元素s只有1個構成元素發生故障時,稱為一重故障;在一重故障下,如果s通過冗余或重構能夠恢復其功能,則認為該一重故障是可重構的。相應的,當s有q個構成元素發生故障時,稱為q重故障;在q重故障下,如果s通過冗余或重構恢復其功能,則該q重故障是可重構的[16]。基于如下規則確定ei1,ei2,…,eiq的故障是否可重構:

規則1在e1,e2,…,em中存在足夠的備件替換ei1,ei2,…,eiq,則ei1,ei2,…,eiq的故障可重構;

規則2通過{e1,e2,…,em}-{ei1,ei2,…,eiq}中元素的重組實現s的功能,從而避免了ei1,ei2,…,eiq故障的影響,則ei1,ei2,…,eiq的故障可重構;

規則3在規定時間內ei1,ei2,…,eiq的故障皆可恢復且不影響s功能,則ei1,ei2,…,eiq的故障可重構。

設s的構成元素為e1,e2,…,em,Re表示某q個構成元素ei1,ei2,…,eiq同時發生故障是否可重構,定義為

(5)

則s的q重可重構度為

(6)

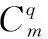
(7)

一重可重構度Re(1)簡記為Re。

由于實際中衛星系統發生一重故障的情形居多,下面以3種典型邏輯關系為例計算一重可重構度。

(1) 串聯。如圖1所示,構成系統s的m個元素e1,e2,…,em是串聯的,說明任意單個元素故障,該系統s元素都無法完成其功能,即各部件的Re(ei)=0,于是

即串聯情況下系統s可重構度為0。

圖1 串聯工作邏輯
Fig.1 Serial working logic

(2)并聯。如圖2所示,構成系統s的m個元素e1,e2,…,em是并聯的,說明任意單個元素故障,該系統都可完成其功能,即各部件的Re(ei)=1,于是

即并聯情況下系統s可重構度為1。

圖2 并聯工作邏輯Fig.2 Parallel working logic

(3)Ω-冗余。以兩種配置的動量輪組件為例進行說明。如圖3所示配置包含3套正裝動量輪(記作X軸、Y軸、Z軸動量輪)和1套斜裝動量輪S,Ω為至少包含3套動量輪的{X,Y,Z,S}的子集的集合,這意味著任意一個動量輪故障,都不會影響姿態控制功能,因此各部件的Re(ei)=1,于是

Re=4/4=1

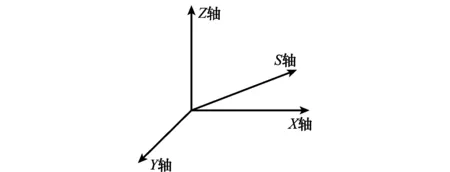
圖3 冗余工作邏輯示例(配置1)Fig.3 Example 1: redundant working logic

如圖4所示配置亦包含3套正裝動量輪X、Y、Z,外加1套備份動量輪Z(。根據三軸姿控原理,Ω={{X,Y,Z},{X,Y,Z′}},這說明備份動量輪Z(只能重構動量輪Z的故障,于是

Re=2/4=0.5

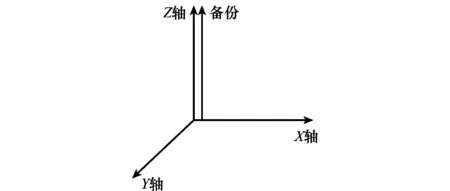
圖4 冗余工作邏輯示例(配置2)Fig.4 Example 2: redundant working logic

2.3 基于可重構度和衛星系統結構樹的評估過程

步驟1構建系統結構樹。根據系統的物理結構確定系統層次結構,以及根據系統功能確定系統各層次元素之間的邏輯關系。

步驟2確定可重構度。根據衛星系統結構樹,逐層確定各層次系統元素的可重構度。

步驟3評估系統健康狀態,其步驟包括:

(1) 確定元素貢獻度。采用層次分析法確定系統結構樹中下一層次各元素對與其關聯的上一層次元素的貢獻度[6];

(2) 計算系統健康度。根據部件健康度、各層次可重構度、各元素貢獻度,由系統結構樹葉節點逐層向上計算各層次系統元素的健康度。設某層元素為s,其下一層元素為e1,e2,…,em,s的可重構度為Re,ei的貢獻度為Wi,ei的健康度為Hi,λ≤1為調整系數,s的健康度為

(8)

3 仿真試驗與分析

以某衛星平臺姿態控制系統故障案例高保真仿真的數據為基礎進行仿真案例分析。根據該案例,衛星特定工作模式下的姿態控制系統結構樹如圖5所示。

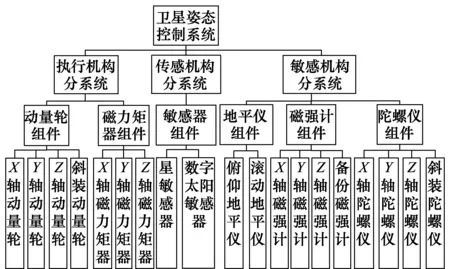
圖5 姿態控制系統結構樹模型Fig.5 Structural tree model of attitude control system

按照物理結構和功能關系劃分為4級層次:系統級、分系統級、組件級和部件級,以系統結構樹中的“敏感機構分系統”為例,進行工作邏輯的說明:

(1) 俯仰地平儀和滾動地平儀以并聯關系構成地平儀組件;

(2)X軸、Y軸、Z軸磁強計和備份磁強計Z′以冗余關系構成磁強計組件,其中X軸、Y軸、Z軸磁強計以并聯關系構成,記為“并聯+冗余”;

(3)X軸、Y軸、Z軸和陀螺儀斜裝陀螺儀S以冗余關系構成陀螺儀組件,其中陀螺儀X、Y、Z以串聯關系構成,記為“串聯+冗余”;

(4) 地平儀組件、磁強計組件以及陀螺儀組件以并聯關系構成敏感機構分系統;

(5)敏感機構分系統、傳感機構分系統和執行機構分系統以串聯關系構成衛星姿態控制系統。

表1中給出某一時刻全部部件的健康度,在此基礎上,演示衛星姿控系統的多級健康度評估算例。按工程領域的做法,經過調整,調整系數λ=6，正則化系數α=1。

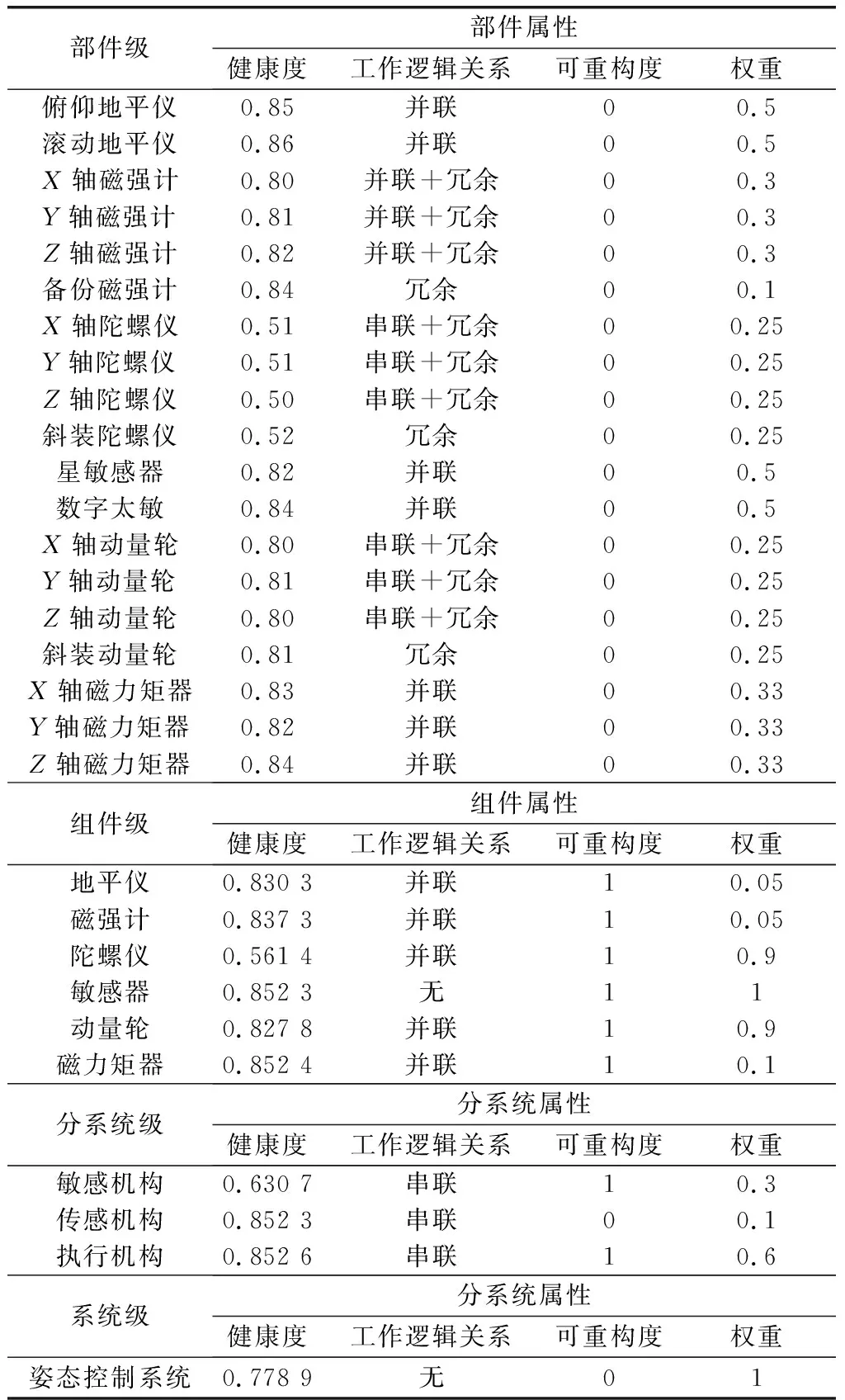
表1 評估算例

下面以陀螺Y緩變故障為例進行衛星姿控系統的多級健康評估。

為評估姿態控制系統的健康度,首先需評估陀螺儀的健康度。根據領域內專家的意見,將陀螺儀的測量輸出作為評估陀螺儀健康度的特征量是工程實際領域通用做法。

陀螺儀是姿態控制系統的重要基礎部件,包括三軸方向X、Y、Z和斜裝方向S共4個陀螺。陀螺儀組件的測量輸出變化如圖6所示,陀螺S、X、Z均視為正常工作,本例重點分析陀螺Y的輸出曲線。從T0時刻到T1時刻,陀螺Y輸出曲線如圖6綠色虛線所示,出現緩變故障,測量輸出時先正常,然后超差,超差幅度不明顯;從T1時刻到T3時刻,陀螺Y測量輸出持續大幅超差,且陀螺在T2時刻已經失效,但系統仍然在使用陀螺Y的輸出數據;從T3時刻到T4時刻,星上計算機判定陀螺Y無效,不再使用陀螺Y輸出數據。

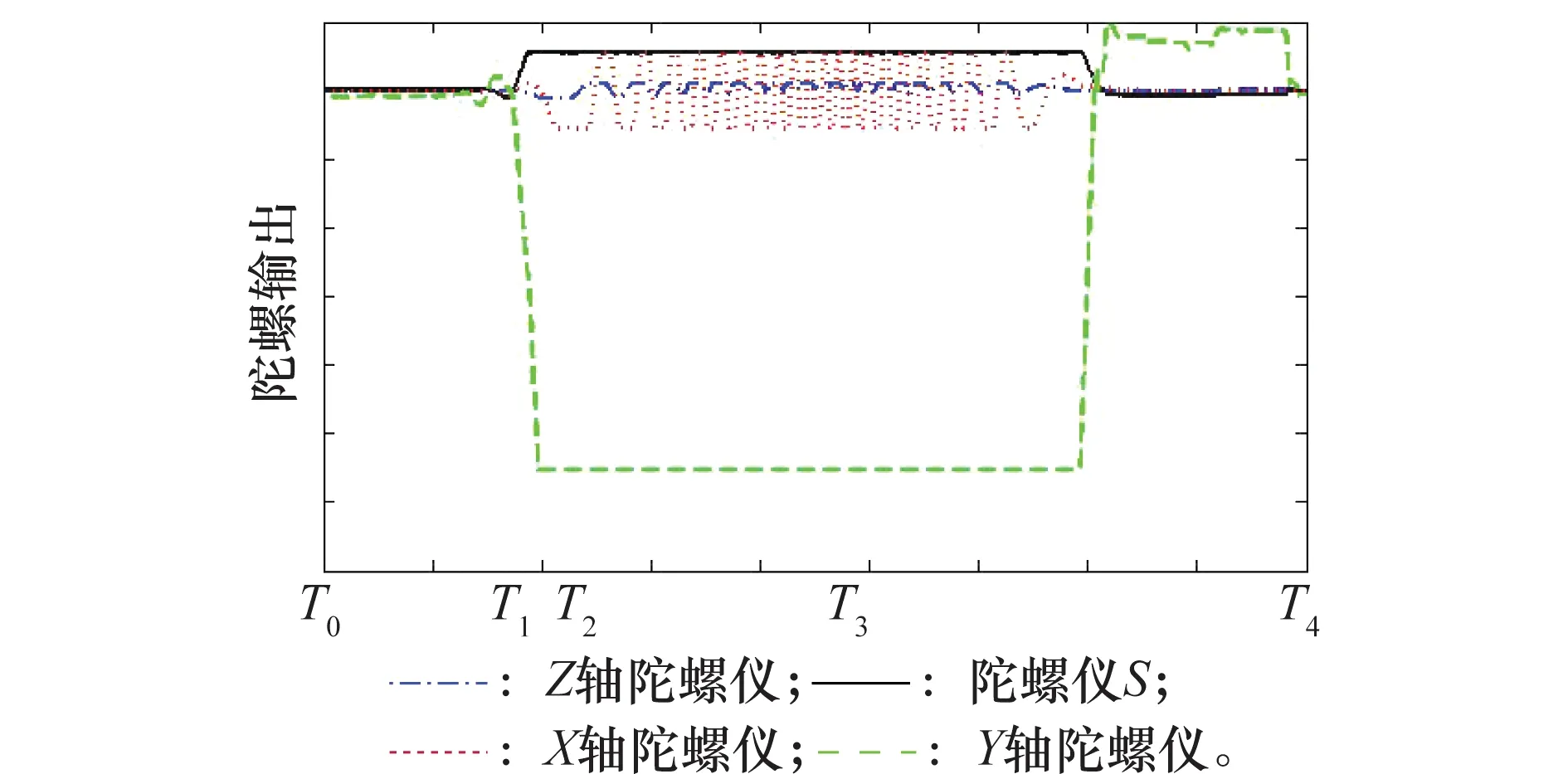
圖6 陀螺儀組件測量輸出變化過程Fig.6 Process of measured output of gyro assembly

動量輪組件控制電壓的變化如圖7所示,除S動量輪控制電壓幾乎不變之外,從T0時刻到T1時刻,當姿態角開始超差時,組件開始調整電壓進行姿態調整;從T1時刻到T2時刻,受姿態角持續大幅超差和Y軸陀螺儀失效的影響,組件進一步調整電壓進行姿態調整;從T2時刻到T3時刻,受星敏感器進入A模式和Y軸陀螺儀失效的影響,組件控制電壓不再調整,姿態角超差幅度不再增大;從T3時刻衛星進入全姿態捕獲模式后,組件不再使用Y軸陀螺儀的測量數據,結合剩余敏感器的測量數據調整控制電壓,小幅變化后恢復原有水平進行姿態調整,最終將姿態角調整到正常范圍內。

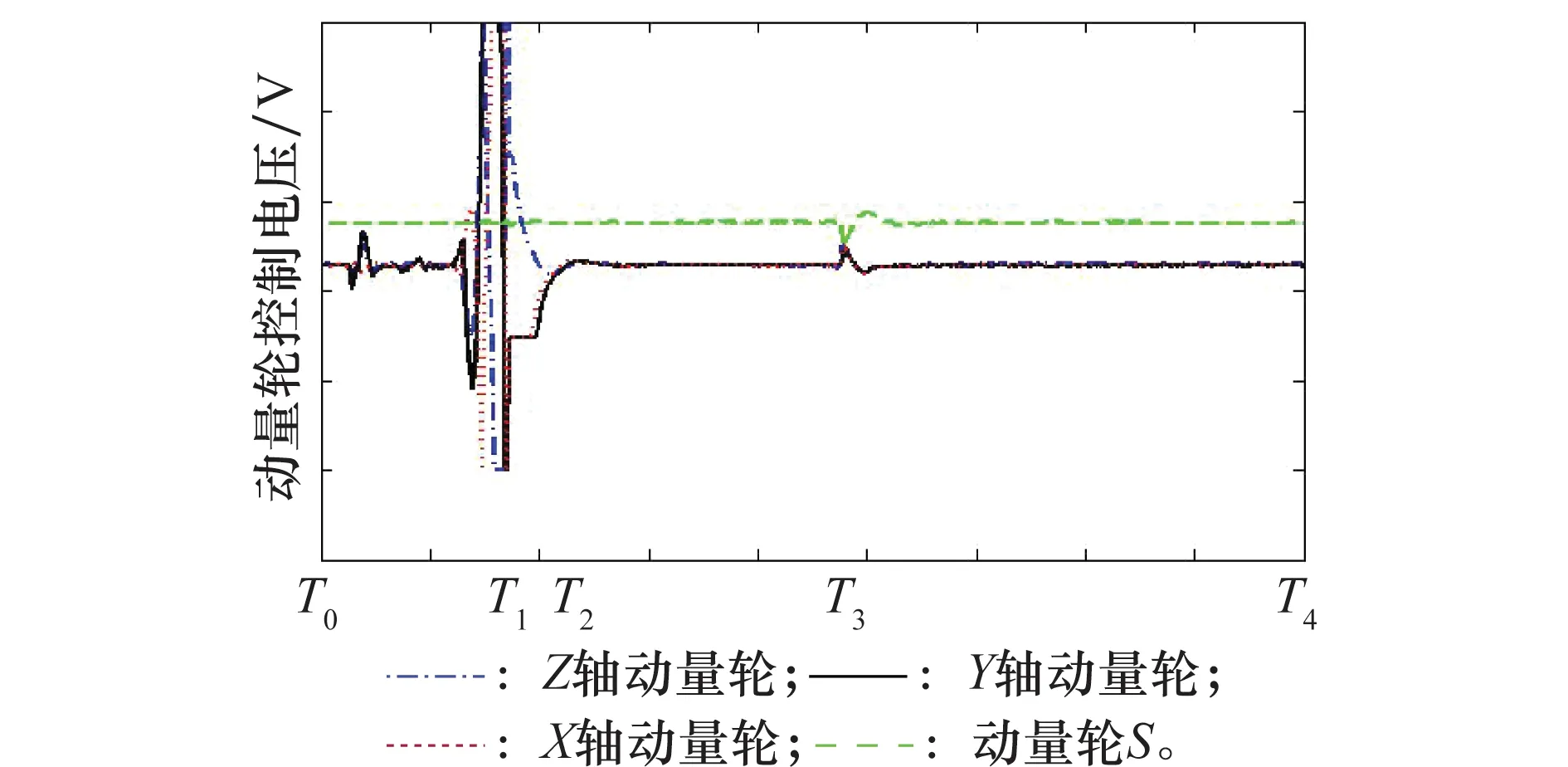
圖7 動量輪組件控制電壓變化過程Fig.7 Process of control voltage of momentum wheel assembly

下面進行部件級的健康狀態評估,為考察影響整個系統健康度的主要因素,在部件層次,選取陀螺儀和動量輪這兩類權重占比大的主要功能部件作為重點考察對象,選取陀螺儀的測量輸出作為評估陀螺儀健康度的遙測參數,選取動量輪的控制電壓作為評估動量輪健康度的遙測參數,其余部件均處于健康狀態,其健康度都取表1中的常數值參與整套方法的健康評估。按照第1.2節的方法實施評估,展示陀螺儀的健康度變化過程,如圖8所示。

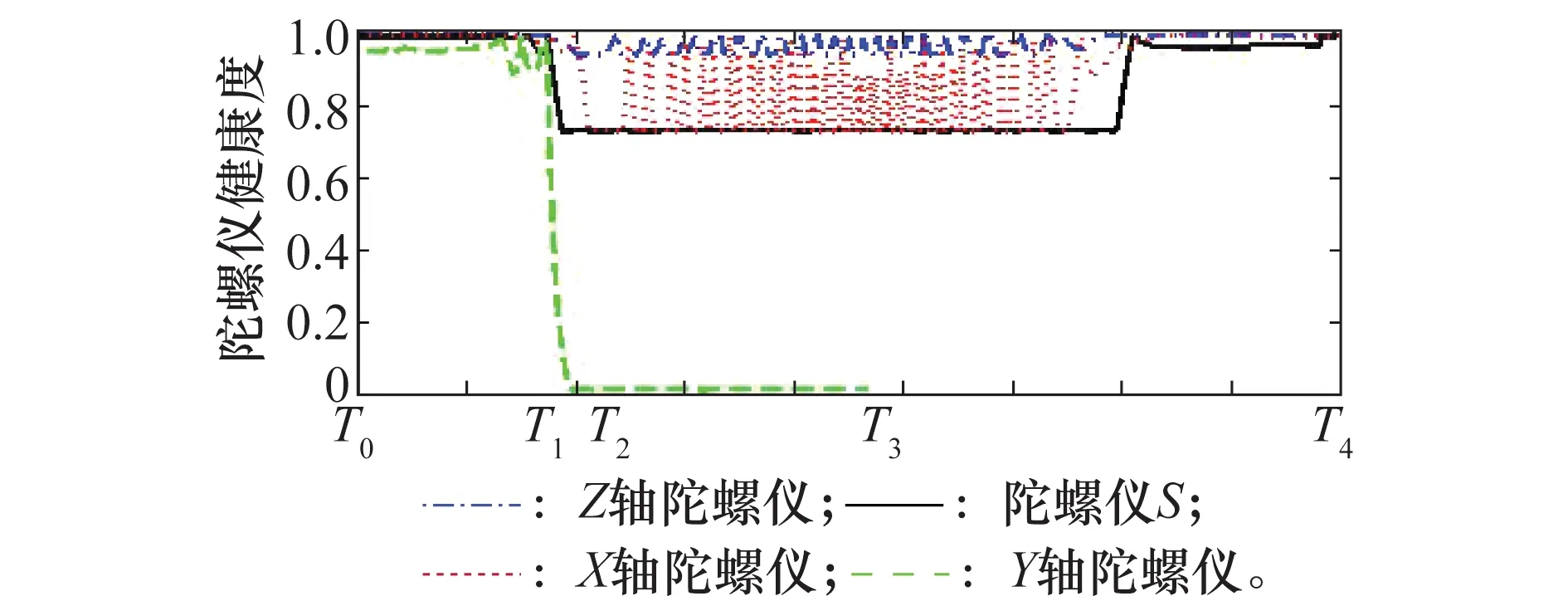
圖8 故障Y陀螺儀和其他陀螺的健康度曲線Fig.8 Health degree of blooey gyro Y and other gyros

從T0時刻到T1時刻,Y軸陀螺儀緩變故障導致其健康度呈小幅波動的不穩定趨勢,從T1時刻到T2時刻,Y軸陀螺儀緩變故障累積效應使其健康度急劇下滑至0,從T2時刻到T3時刻,其健康度維持在0的最低水平上,T3時刻以后,星上計算機不再使用Y軸陀螺儀的數據,對Y軸陀螺儀的健康評估隨之停止,由此可見,對Y軸陀螺儀的健康評估與實際情況具有相當好的一致性。對其他陀螺的健康評估而言,受故障Y軸陀螺儀的影響,各自的健康度均有一定程度的波動,但基本維持在較高的水平(0.7～0.9)上,因此對其他陀螺的健康評估符合實際。

在完成部件的健康評估后,下面進行部件級到系統級的綜合評估,如圖9所示。

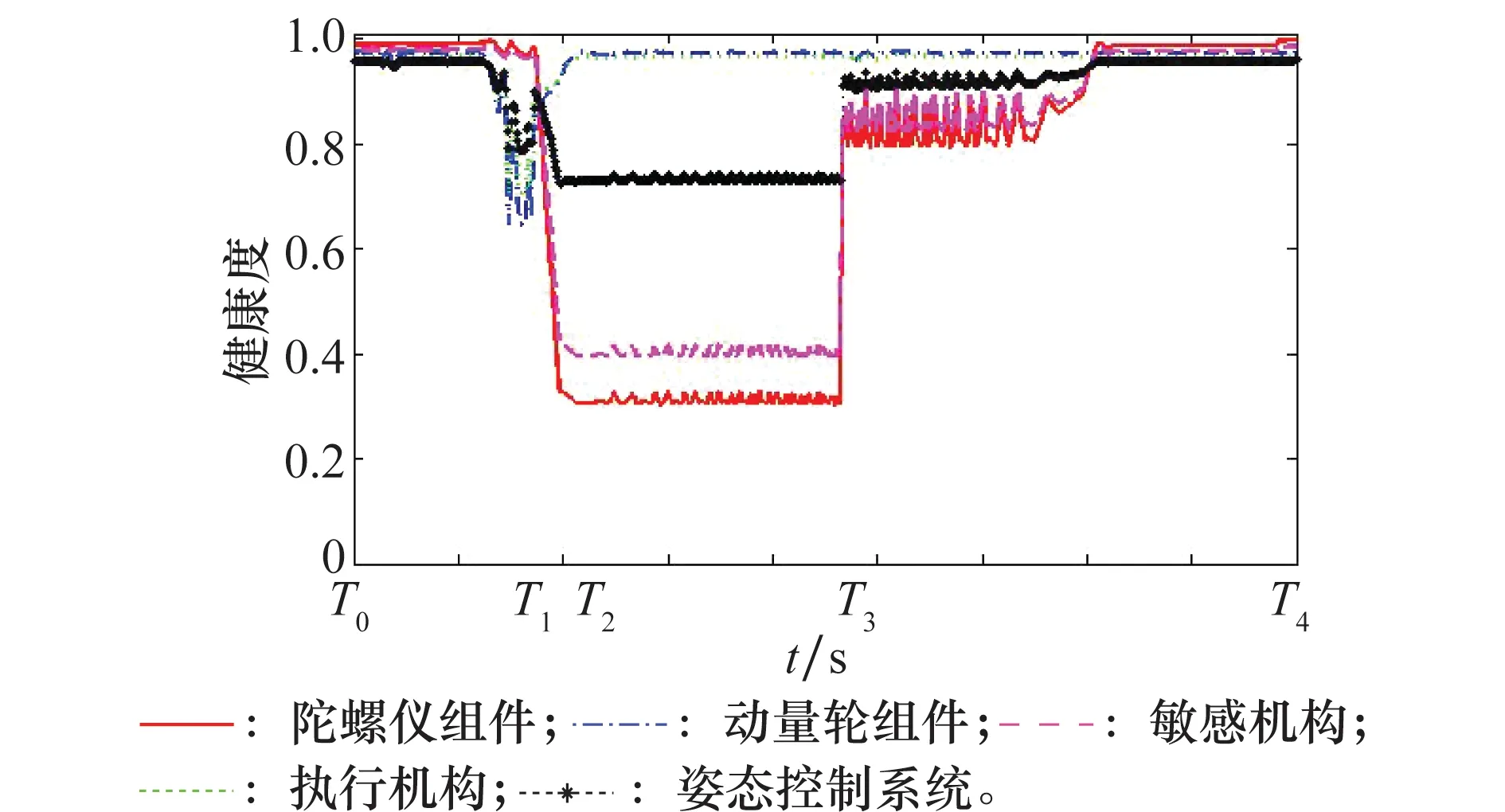
圖9 姿態控制系統多級健康度曲線Fig.9 Health state of multi-level of attitude control system

從T0時刻到T1時刻,受Y軸陀螺儀緩變故障影響,陀螺儀組件的健康度處于不穩定狀態,且存在下降趨勢,由于姿態角開始超差引發動量輪進行姿態調整,動量輪接收Y軸陀螺儀的測量數據,動量輪組件的健康度也呈不穩定和下降趨勢,進一步地,各分系統和姿控系統的健康度均有不同幅度的波動,呈現不穩定和下降趨勢;從T1時刻到T2時刻,Y軸陀螺儀緩變故障累積效應使其健康度急劇下滑至0,直接導致陀螺儀組件的健康度迅速下降到非常低的水平(0～0.3),敏感機構分系統的健康度也因此迅速下降到較低水平(0.3～0.6),與此同時,動量輪組件使用Y軸陀螺儀的超差數據對進行姿態的大幅調整,試圖使系統姿態恢復,但效果適得其反,動量輪組件逐漸減小控制電壓,恢復到原有水平,動量輪組件及執行機構分系統健康度隨之恢復到原先的健康的水平(0.9～1);從T2時刻到T3時刻,是整個系統的平穩期,星上計算機通過診斷發現Y軸陀螺儀失效,系統各級的健康度水平維持在之前的水平;從T3時刻以后,陀螺儀組件采取故障重構策略:不再使用Y軸陀螺儀的數據,Y軸陀螺儀不再參與健康評估,因此陀螺儀組件的組成由{X軸陀螺儀,Y軸陀螺儀,Z軸陀螺儀,陀螺儀S}變為{X軸陀螺儀,Z軸陀螺儀,陀螺儀S},其可重構度由1變為0,舍棄陀螺Y后重新進行健康評估,陀螺儀組件的健康度恢復到較高水平(0.7～0.9),敏感機構分系統的健康度也恢復到較高水平,系統的健康度恢復到健康水平(0.9～1)。由此可見,可重構度的引入,在刻畫系統高冗余、高可靠性和非線性等復雜特性同時,也使系統健康評估的結果更加符合客觀實際,降低了健康評估的主觀性。

下面分析系統健康度與實際情況的符合程度。從姿態角表征的角度,不考慮部件故障,僅根據圖8的3個姿態角利用非參數回歸的方法計算系統姿態角健康度,再求其加權平均,以此作為姿控系統健康度的對比標準[6]。仿真案例中認為姿態角的正常取值在0°附件,上下浮動2°,敏感機構故障,引發執行機構連鎖反應,但執行機構正常,所以該對比標準基本合理。

仿真案例中姿態角的變化如圖10所示,從T0時刻到T1時刻,受Y軸陀螺緩變故障影響,姿態角發生細微震蕩;從T1時刻到T2時刻,受Y軸陀螺失效及其測量輸出持續超差的影響,姿態角發生大幅變化;從T2時刻到T3時刻,姿態角持續超差,且Y軸陀螺測量輸出持續超差,星上計算機判定衛星滿足模式切換條件,在T3時刻進入全姿態捕獲模式;從T3時刻到T4時刻,星上計算機不再使用Y軸陀螺的輸出數據,利用剩余敏感器的測量數據調動動量輪組件進行姿態調整,最終將姿態角穩定在正常范圍內。

圖10 姿態控制系統的姿態角變化過程Fig.10 Process of attitude angles of attitude control system

根據3個姿態角建立評估標準得到系統健康度評估結果和基于可重構度的方法評估結果對比情況如圖11所示。

圖11 姿態控制系統健康度曲線Fig.11 Health state of attitude control system

從圖11的系統健康度結果容易發現,從T0時刻到T1時刻,兩者的健康度水平均維持在健康水平附件,不同之處在于:Y軸陀螺緩變故障引起系統健康度的波動在基于可重構度的方法評估結果中更加明顯;從T1時刻到T2時刻,Y軸陀螺故障的累積效應使得系統健康度快速下降,兩類方法的結果對此都有所體現,不同之處在于前者方法評估的系統健康度下降到較高水平(0.7～0.9),后者下降到較低水平(0.3～0.6),分析認為有兩點原因導致差異:其一,兩者使用的量綱不一致使得評估結果的水平不一致,其二,系統各級存在的可重構特性使得系統不會因為單個部件故障就下降到較低水平,從這個角度考慮,前者方法的評估結果更加合理;從T2時刻到T3時刻是系統健康度的平穩期,兩類方法的評估結果基本維持在原先水平;T3時刻,系統執行故障重構策略:不再使用Y軸陀螺的測量數據,從T3時刻到T4時刻,兩類方法的評估結果中系統健康度都在上升,區別在于:前者迅速恢復到健康水平(0.9～1),后者以較大的波動(標準差為0.1365,均值0.7611)維持在較高水平(0.7～0.9),分析認為差異產生的原因也是兩點:其一,兩者使用的量綱不一致使得評估結果水平不一致,其二,基于姿態角標準方法使用的姿態角數據較大的波動性傳遞到評估過程中,造成健康度的較大波動性。從評估結果的平穩角度考慮,前者更加平穩。

綜上所述,本文提出的方法確實具有合理性,對于衛星系統的健康評估、故障診斷以及健康管理具有實用意義。

4 結 論

本文針對在軌衛星的健康評估問題,提出基于可重構度的在軌衛星多級健康評估方法,并以姿態控制系統為例進行了仿真分析。結果表明該方法具有較好的合理性,尤其是可重構度的引入,較好地解決了衛星系統高冗余、高可靠性和非線性等復雜特性的刻畫問題,降低了評估的主觀性。該方法經過遷移,可以用于除衛星系統以外的具有高冗余、高可靠性特性的系統評估,可拓展性強。

此外,本文方法存在以下幾點不足,需要進一步拓展研究:第一,在部件健康評估的方面,需要進一步研究多參數特征量對于部件以及系統健康評估的影響;第二,基于二重可重構度甚至更高重可重構度的健康評估有待實例驗證;第三,本文提出的方法有待更多實例和實測數據的驗證。