天基紅外低軌衛星引導反導作戰能力需求分析

劉錦昌, 黃樹彩, 趙 煒, 龐 策, 黃 達

(空軍工程大學防空反導學院, 陜西 西安 710051)

0 引 言

天基紅外低軌預警系統也稱天基跟蹤與監視系統(space tracking and surveillance system, STSS)是美國天基紅外系統(space based infrared system, SBIRS)的低軌部分[1-4],是美國反導預警系統的重要組成部分,該系統包括20到30顆部署高度為1 600 km的低軌(low earth orbit, LEO)衛星,衛星上裝有捕獲和跟蹤兩種相機,捕獲相機為寬視場小口徑相機,工作波段為0.7～3 μm,用于掃描檢測目標,跟蹤相機為窄視場大口徑多色相機,有兩種工作波段分別為3～8 μm和8～12 μm,可用于跟蹤不同溫度的目標。捕獲相機發現目標后,將目標信息傳送給跟蹤相機。跟蹤相機可以采用臨邊探測的方式持續跟蹤飛行中段和再入段的目標,并有分辨識別彈頭與誘餌的能力。LEO衛星間可以通過60 GHz的星間通信鏈路來實現雙星觀測并通過交叉定位進行精確跟蹤。STSS系統不僅可以實現對彈道導彈目標的跟蹤,還可以跟蹤反導攔截系統的攔截彈。信息處理系統利用導彈狀態信息進行彈道預報及預測命中點的計算并引導攔截系統對導彈進行攔截。衛星的跟蹤能力決定了彈道預報的精度以及預測命中點的誤差,攔截系統則要求預測命中點的誤差必須高到攔截器的機動能力能夠修正的程度。

當前,對于彈道導彈中段的跟蹤工作的研究主要集中在中段運動建模[5]及濾波算法[6]等方面,對于LEO衛星對中段飛行的導彈的跟蹤能力的研究很少,衛星的觀測方程及導彈的狀態方程均為非線性方程,對導彈的位置估計及跟蹤問題屬于非線性濾波的問題,非線性濾波的方法多種多樣,包括擴展卡爾曼濾波[7](extended Kalman filter, EKF),無跡卡爾曼濾波[8](unscented Kalman filter, UKF),粒子濾波[9]及其各種改進算法,但是,為了要衡量LEO衛星的跟蹤能力,需找到各種濾波算法跟蹤精度的上界,即跟蹤誤差的下界,傳統的跟蹤誤差下界用克拉美羅限(Cramer-Rao lower bound, CRLB)[10-17]表示,但是CRLB沒有考慮跟蹤過程的過程噪聲,衛星的觀測及模型屬于動態模型,含有過程噪聲,因此,這里引入后驗CRLB(posterior CRLB, PCRLB)來衡量衛星的跟蹤能力,得到衛星跟蹤能力與衛星星載探測器技術指標的關系。

對于LEO衛星信息支持的反導系統而言,由于彈道導彈目標的飛行速度較快,一般采用基于預測命中點[18-19](predict intercept point, PIP)的制導控制方法,目前對于PIP的研究大多集中在空氣動力學目標[12],并且不考慮由于目標的狀態誤差而導致的PIP誤差的影響。目標的預測狀態誤差與衛星的跟蹤能力有關,采用橢圓軌道線性化方程的方法可以計算預測彈道的誤差,將衛星的跟蹤誤差引入PIP的計算,可得到由衛星引導下的反導系統PIP誤差。攔截彈發射后會朝向PIP飛行,隨著PIP的變化及精度的提高,攔截彈也會隨之調整飛行軌跡,始終朝向更新的PIP飛行。

目前,國內對于PIP對攔截器中段和末段飛行的影響研究大多集中在控制規律及制導規律的研究[20-22],關于PIP誤差對修正能力的影響的研究較少。對于攔截彈修正能力的研究,文獻[23]研究了大氣層外攔截基于任務圖優化的脈沖點火策略,研究了點火時機對修正能力的影響,文獻[24]分析了薩德攔截系統中外部信息提供的預測命中精度對中段機動需求的影響,本文采用均勻點火策略分析PIP精度對攔截彈中段飛行的修正能力的影響。文獻[25]采用了可信性理論分析標準攔截彈的末段修正能力,本文基于此模型分析了攔截彈的末段修正能力并建立了末段修正能力與中末飛行段交接班時刻PIP誤差的關系。

1 LEO衛星跟蹤能力分析

1.1 模型建立

1.1.1 彈道導彈運動模型

導彈中段僅受重力影響,因此在地心慣性坐標系下的運動模型為

(1)

式中,r=(x,y,z)T和v=(vx,vy,vz)T分別表示導彈目標的位置矢量和速度矢量;μ是地球的引力系數。由于自由段飛行時會受到攝動力的影響,運動模型會有一定的誤差,因此,導彈的狀態方程可寫成

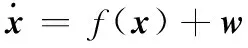
(2)

式中,f(x)表示導彈的運動模型,自由段狀態變量為x=(x,y,z,vx,vy,vz)T;w表示模型的誤差,通常假設是高斯白噪聲。

1.1.2 LEO衛星觀測模型

(3)

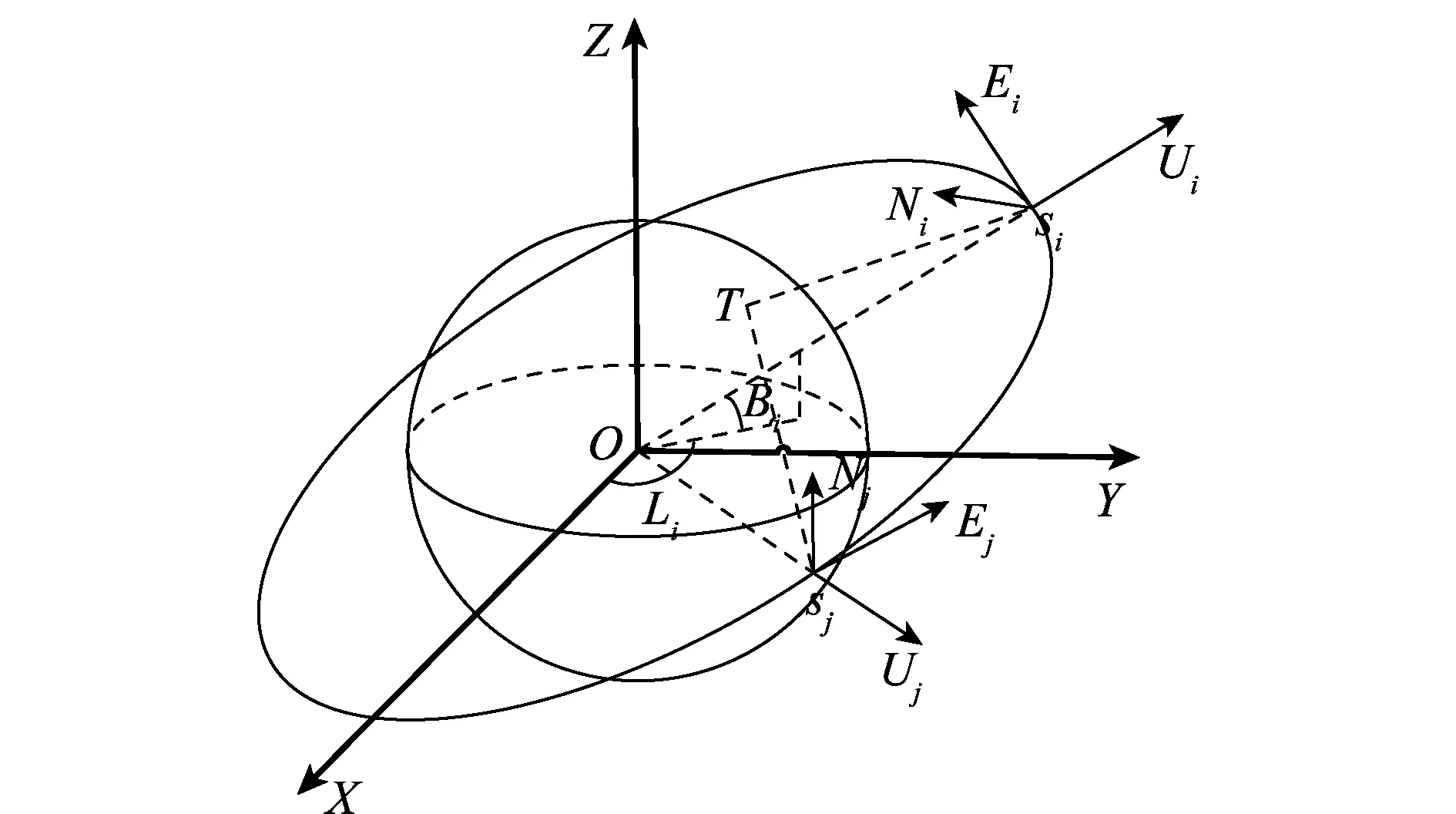
圖1 LEO衛星雙星觀測Fig.1 LEO satellite binary observation

衛星到目標視線的方位和俯仰角信息分別為αi和ei,則

(5)

衛星測量方程可表示為

zi=hi(x)+νi=[αi,ei]T+νi

(6)

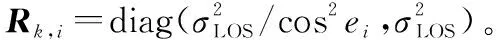
1.2 跟蹤性能估計

1.2.1 PCRLB計算

彈道目標的狀態方程經過離散化可得

xk+1=xk+f(xk)(tk+1-tk)+Gwk=

xk+f(xk)·T+Gwk=fk(xk)+Gwk

(7)

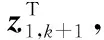
h(xk+1)+νk+1

(8)

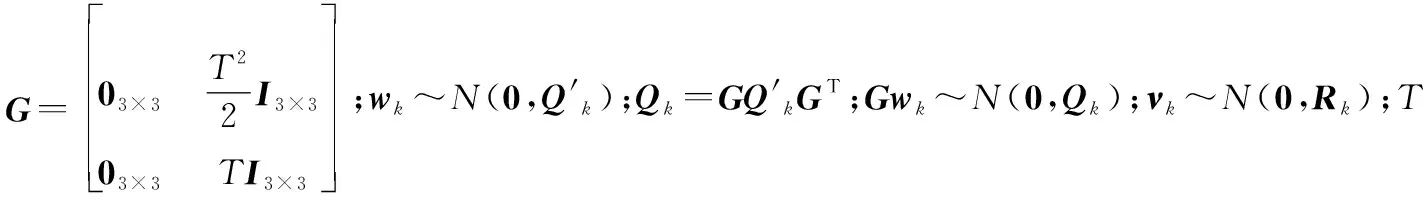
(9)

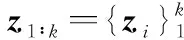
xklnp(z1∶k,x1∶k)]T}

(10)

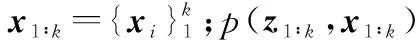
(11)

(12)

(13)

(14)

(15)

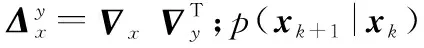
在高斯白噪聲條件下,由式(7)和式(8)有

(16)

(17)

則

(18)

(19)

由式(12)～式(15)及式(18)、式(19)可得

xkfk(xk)]

(20)

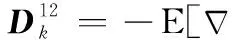
(21)

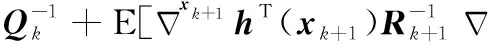
(22)

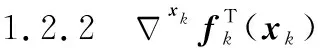
由離散化的彈道目標狀態方程式(7)可得

(23)

經推導可得

(25)

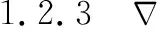
由雙星觀測方程式(8)可得

(26)

(27)

1.2.4 期望計算

式(20)～式(22)涉及到數學期望的計算,傳統的方法是利用蒙特卡羅方法進行近似計算,由于采用的是隨機采樣的方法,計算樣本的數目一般較多,文獻[26-29]提出了無跡變換的思想,無跡變換采用確定性采樣,可以大大減少樣本的個數,提高可計算的效率,算法的具體流程如下:

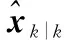
步驟2根據無跡變換計算Sigma采樣點,即

(28)

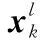
將采樣點值代入式(20)和式(21)，可得

xkfk(xk)]=

(29)

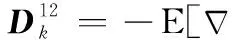
(30)

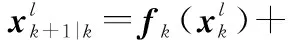
xk+1h(xk+1)]=

(31)

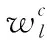
將式(29)～式(31)代入式(11)即可得到Jk,從而得到LEO衛星觀測的PCRLB,將位置和速度跟蹤PCRLB分別定義為Pr,k和Pv,k,則

(32)

(33)

式中,Pk(i,i)表示矩陣Pk的第i個對角線元素值。

2 PIP誤差計算

PIP是根據彈道導彈目標和攔截彈的運動規律計算出目標與攔截彈相遇的空間位置。計算PIP首先要預測彈道導彈目標的狀態,得到彈道導彈目標的預測彈道,然后根據目標的預測彈道和攔截彈的動力學性能計算PIP的位置,最后,計算由于衛星的跟蹤誤差而導致的PIP的誤差大小。

2.1 目標狀態預測

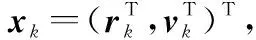
(34)

(35)

令

h=rk×vk

(36)

式中

‖

(37)

(38)

(39)

Et滿足

(40)

可通過牛頓迭代法求得偏近點角Et。

2.2 目標狀態預測誤差

由于目標的狀態估計是存在誤差的,那么估計預測彈道也是有一定誤差的,直接在慣性坐標系下計算彈道預測誤差比較復雜,可以通過RSW坐標系將三維預測問題變為二維預測問題,使預測誤差的計算簡化。

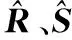
(41)

(42)

(43)

(earth-centred inential,ECI) 慣性坐標系到RSW坐標系的轉換矩陣為

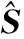
(44)

紅外LEO衛星在tk時刻估計的目標在慣性坐標系下的誤差協方差為PECI,k,在tk時刻目標在RSW坐標系下的狀態誤差協方差為PRSW,k,則

(45)

式中

(46)

目標在RSW坐標系下跟據tk時刻信息預測t時刻的狀態誤差協方差為PRSW,k(t),令J2是xRSW,k到xRSW,k(t)的狀態轉移矩陣,即

xRSW,k(t)=J2(t-tk)xRSW,k

(47)

則

(48)

對于J2(t-tk)的計算,Tschauner與Hempel得到了橢圓軌道線性化方程以及的偏近點的解析解,即T-H方程。Lawden得到了在積分函數下的T-H方程的閉合求解方式,文獻[30]在前人的基礎上根據T-H方程求出了轉移矩陣J2(t-tk),推導過程及J2(t-tk)的表達式較復雜,具體可參考文獻[30],此處不再贅述。

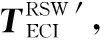
(49)

式中

(50)

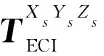
(51)

式中,qβ為視線方位；qε為視線俯仰角。

目標在視線坐標系下跟據tk時刻信息預測的t時刻的狀態誤差協方差為Ps,k(t),則

(52)

式中

(53)

由式(45)、式(48)、式(49)、式(51)可得由PECI,k到Ps,k(t)的計算公式為

(54)

根據位置和速度狀態誤差可以將Ps,k(t)分塊為

(55)

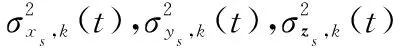
(56)

要消除σcro,k(t)的影響需要攔截彈進行軌道修正,而攔截器中末段的軌道修正能力是有限的。根據3σ準則,要保證成功攔截,3σcro,k(t)的大小不能超過攔截彈的軌道修正能力。

2.3 PIP及其誤差

完成對彈道導彈目標的彈道預測后,就可以進行PIP的計算。PIP的計算需要考慮攔截彈的動力學特性。反導攔截彈的飛行過程一般分為助推段、中段和末段。在助推段,攔截彈會按照初始裝訂的參數進行方案飛行,在計算PIP時,假設助推段彈道傾角是以恒定的角速度變化的。

攔截彈助推段飛行傾角近似公式為

(57)

(58)

(59)

式中,r*=(x*,y*,z*)表示假設的PIP的位置向量;rd0=(xd0,yd0,zd0)表示攔截彈發射點的位置向量;tbo,3時刻助推段結束。

助推段結束后,中制導段朝向PIP進行飛行,末制導依靠導引頭探測目標進行自尋的飛行。因為中段PIP的變化時非常緩慢的,所以中制導段可以看成朝著一個固定的點或者運動速度非常慢的點飛行,認為攔截彈是以勻速飛向PIP,設攔截彈在thit時刻運動到PIP, 則

(60)

式中,rd(tbo,3)表示助推段結束時刻攔截彈的位置向量;vd(tbo,3)表示助推段結束時刻攔截彈的運動速度。

PIP的計算過程如下:

步驟1紅外LEO衛星最早捕獲目標的時刻為tmin,從此刻開始進行PIP及誤差的計算,令k=0,tk初始值為tmin。

步驟2紅外LEO衛星根據tk時刻目標的狀態信息xk預測出目標的落點位置rk(tl)及落點時刻tl;

步驟3令ta=tk,tb=tl,則PIP的時刻tc應該在ta和tb之間,迭代過程的PIP時刻初始值為tc=(ta+tb)/2,根據xk預測tc時刻導彈位置向量為rk(tc),即PIP時刻彈道導彈位置。

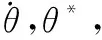
步驟5將彈道導彈飛到PIP的時刻tc與攔截彈飛到PIP的thit進行比較。如果tc-thit>ε,則表明PIP的時刻取的較大,應減小PIP時刻,所以令tb=tc,如果thit-tc>ε,則表明PIP的時刻取的較小,應增大PIP時刻,所以令ta=tc,重新計算PIP位置和tc-thit的大小,直到滿足|tc-thit|<ε為止。

步驟6PIP位置的高程為h,距離攔截彈發射點的遠程為r,攔截系統最高的攔截高程為hmax,最遠的攔截距離為rmax,如果h>hmax或r>rmax,說明攔截彈的發射時刻較早而導致攔截彈的飛行時間thit-tf過長,所以要推遲攔截彈的發射時間tf,令tf=tf+Δtf。

步驟7如果滿足攔截彈攔截的高程和遠程要求,最后所得到的預測出的命中點位置向量為r*=rk(tc),PIP時刻為t*=tc。

步驟8根據tk時刻導彈狀態誤差協方差矩陣PECI,k預測得到t*時刻導彈狀態誤差協方差矩陣Ps,k(t*),計算σcro,k(t*)。

步驟9令tk=tk+T,k=k+1,返回步驟2,進行下一時刻的PIP計算。

步驟10如果‖rd(tk)-rk‖≤dIR,dIR為攔截彈導引頭最大作用距離,進入攔截彈末制導階段,不需要外部信息提供PIP,記tend=tk為末段開始時刻,仿真終止。

3 攔截彈中末段修正能力分析

3.1 攔截彈中段修正能力

攔截彈在中段飛行時會利用PIP的信息進行軌道修正,設中段飛行進行n次軌道機動,中段飛行時間段為[tmid min,tmid max],如果不考慮初中段交接班時間間隔和中末端時間間隔,則tmid min=tbo,3,tmid max=tend,中段第i(i=1,2,…,n)次機動的時刻為tmid ,i,有

(61)

設tmid min時刻的PIP誤差為3σcro mid,0(t*),tmid ,i時刻PIP誤差為3σcro mid,i(t*),第i次機動需要消除的最大距離為dmax,i,(i=1,2,…,n),則

dmax,i=3σcro mid, i+1(t*)-3σcro mid,i(t*)

(62)

第i次機動需要的最大轉移速度為vmax,i(i=1,2,…,n),則

(63)

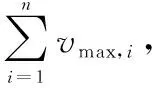
(64)

式中,vmid,max應滿足vmid,max≥vmax；Isp為燃料比沖;mKV為攔截器動能攔截器總質量;mmid為中段燃料總質量;τ1為燃料燃燒效率;τ2為燃料用于軌控的比例。

3.2 攔截彈末段修正能力

攔截器中段飛行后,整流罩拋罩,中末交接班結束后,不再利用外部傳感器提供目標信息,而是利用自身紅外導引頭進行目標探測,進行自尋的制導。由于攔截器末制導段的飛行時間很短,末制導的初始時刻的PIP誤差的大小等于末制導初始時刻的零控脫靶量大小,即攔截器不加任何修正的脫靶距離。

攔截器的末制導段的最大可消除零控脫靶量大小為ZEMmax,則

ZEMmax=

(65)

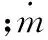
攔截器要實現成功攔截,必須保證攔截器的末制導段的最大可消除零控脫靶量大于初始PIP的誤差大小,即滿足

ZEMmax≥3σcro,end(t*)

(66)

式中,3σcro,end(t*)為tend時刻PIP誤差。

4 仿真及分析

設計典型的反導防御系統攻防對抗場景,彈道導彈目標為3 500 km彈道導彈,發射經緯度為(25°N,130°E),發射方位角為130°,LEO預警衛星的星座構型為28/4/0:50°,軌道高度為1 600 km,起始觀測時刻為彈道導彈助推段關機時刻,采樣周期T=2 s,視線角誤差σLOS=60 μrad,文獻[17]提供的攔截系統的性能參數如表1所示。根據表1提供的數據可得攔截彈的中段飛行力所能提供的最大轉移速度vmid,max=223.2 m/s,攔截器末段燃料最長消耗時間tburn,max=9.3 s,攔截3 500 km的彈道導彈的末段飛行時間為tburn=6.56 s,末段最大可消零控脫靶量為663.7 m。

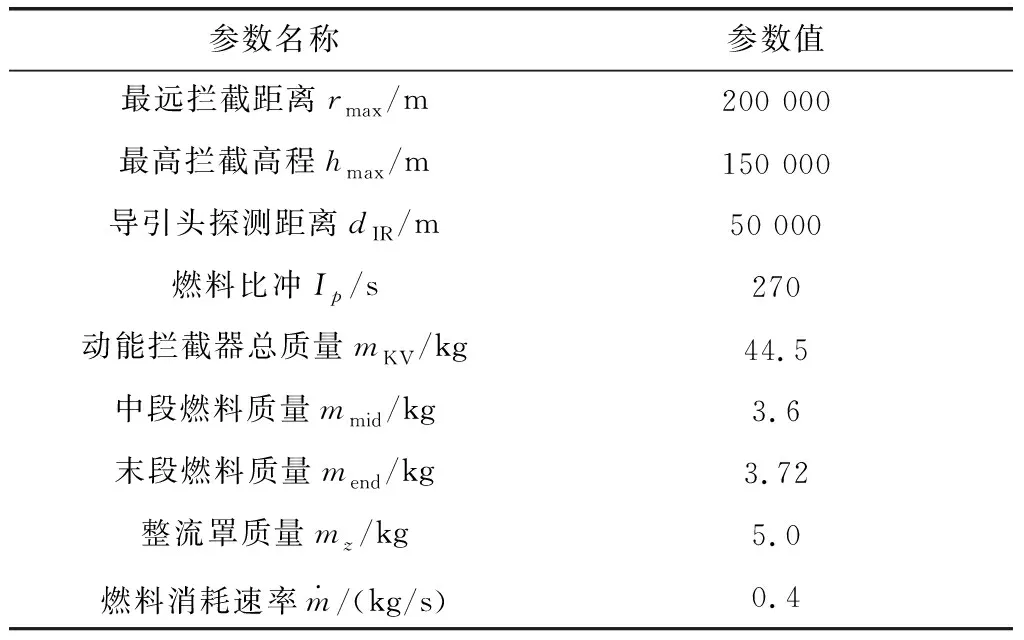
表1 攔截系統的性能參數

4.1 LEO衛星跟蹤能力仿真

(1) 視線角度誤差對跟蹤能力的影響

分析視線角度誤差對跟蹤能力的影響,保持采樣周期T=2 s不變,觀測角度誤差分別取σLOS=30 μrad、60 μrad、90 μrad、120 μrad,位置和速度跟蹤誤差的PCRLB下界如圖2和圖3所示,可以看出視線角誤差會影響位置PCRLB的大小而基本不影響速度PCRLB的大小,觀測角誤差越小,位置穩定跟蹤誤差越小。

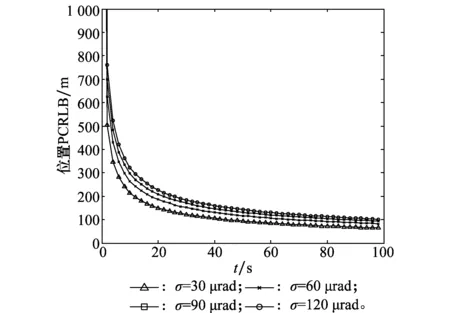
圖2 測角誤差對位置PCRLB影響Fig.2 Effect of angle measurement error on position PCRLB

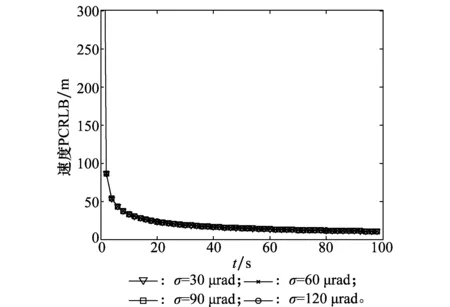
圖3 測角誤差對速度PCRLB影響Fig.3 Effect of angle measurement error on velocity PCRLB

(2) 采樣頻率對跟蹤能力的影響

分析視線角度誤差對跟蹤性能的影響,保持采樣視線觀測誤差σLOS=60 μrad不變,采樣周期分別1 s、2 s、4 s,位置和速度跟蹤誤差的PCRLB如圖4和圖5所示,可以看出,采樣周期對位置和速度PCRLB的大小都有影響,采樣周期越小,位置和速度的穩定跟蹤誤差越小。

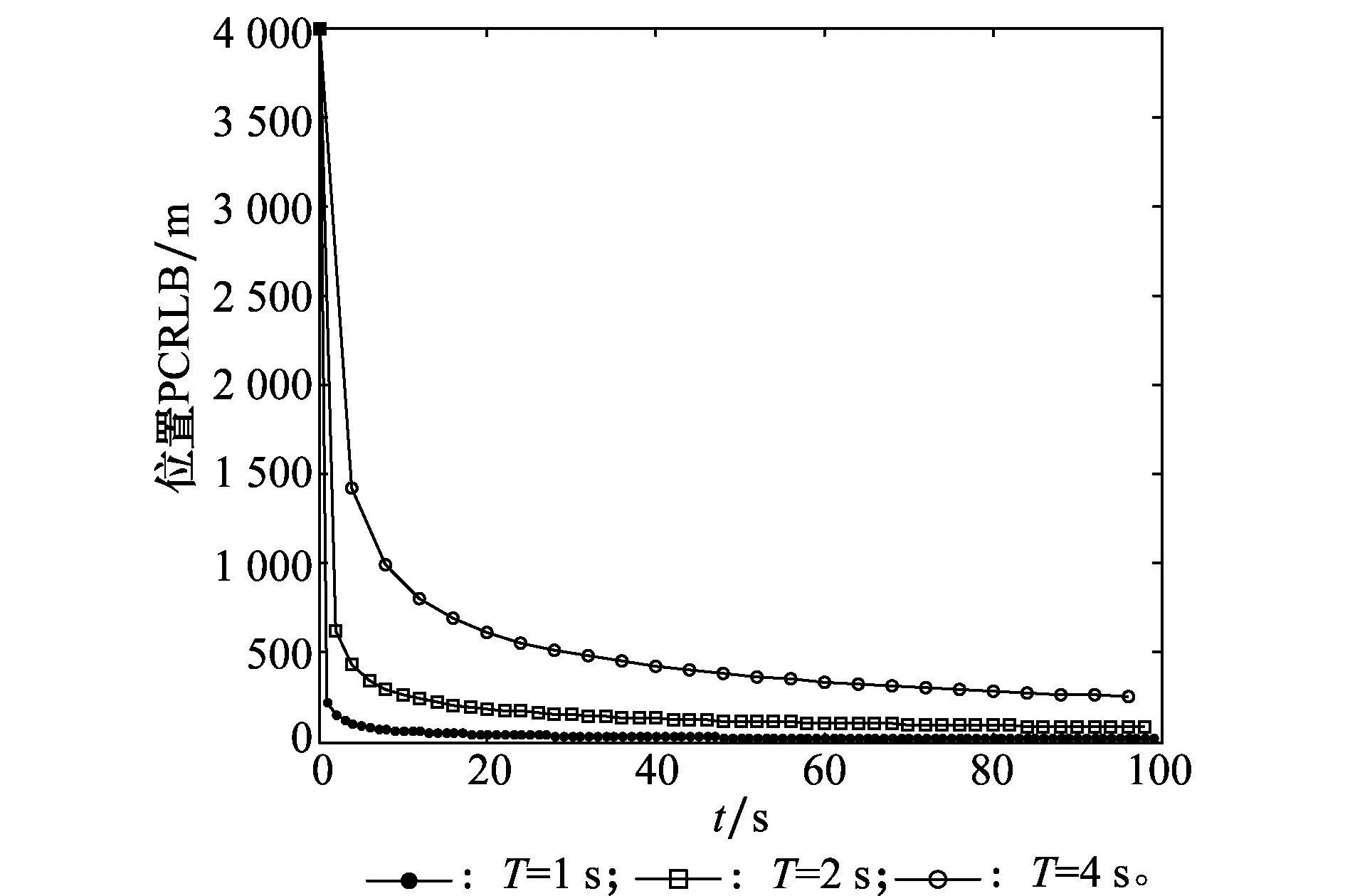
圖4 周期對位置PCRLB影響Fig.4 Effect of measurement period on position PCRLB

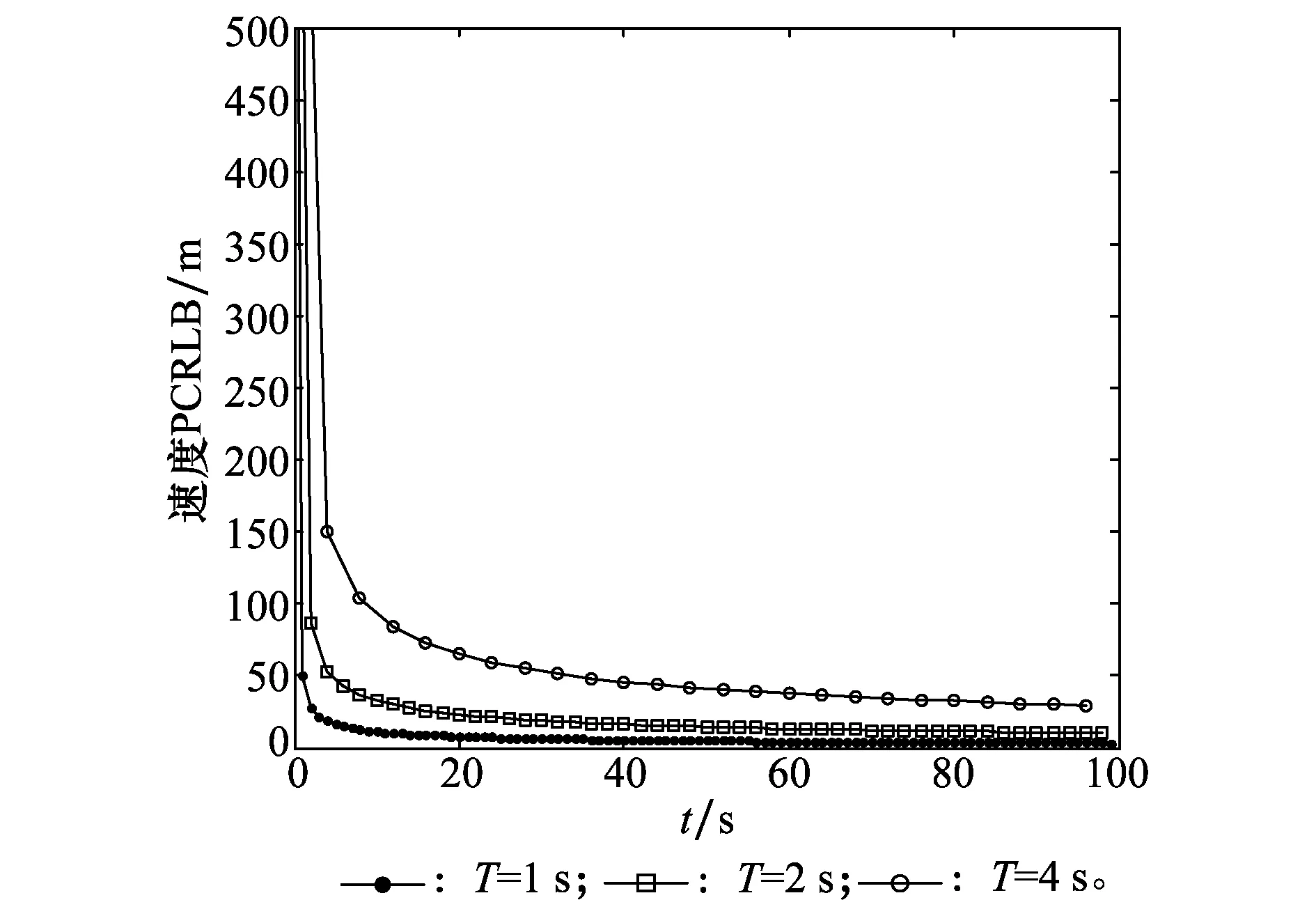
圖5 周期對速度PCRLB影響Fig.5 Effect of measurement period on velocity PCRLB

4.2 PIP誤差變化曲線

(1) 視線角度誤差對PIP誤差的影響

視線角誤差會影響對彈道導彈目標的穩定跟蹤精度,進而影響PIP誤差的大小,圖6為攔截彈飛行中段的PIP的精度隨時間的變化曲線,橫坐標以攔截彈發射時刻為0時刻,縱坐標表示3σPIP誤差的大小。可以看出保持采樣精度T=2 s不變,隨著觀測角誤差的減小,每時刻PIP的精度會逐漸降低。

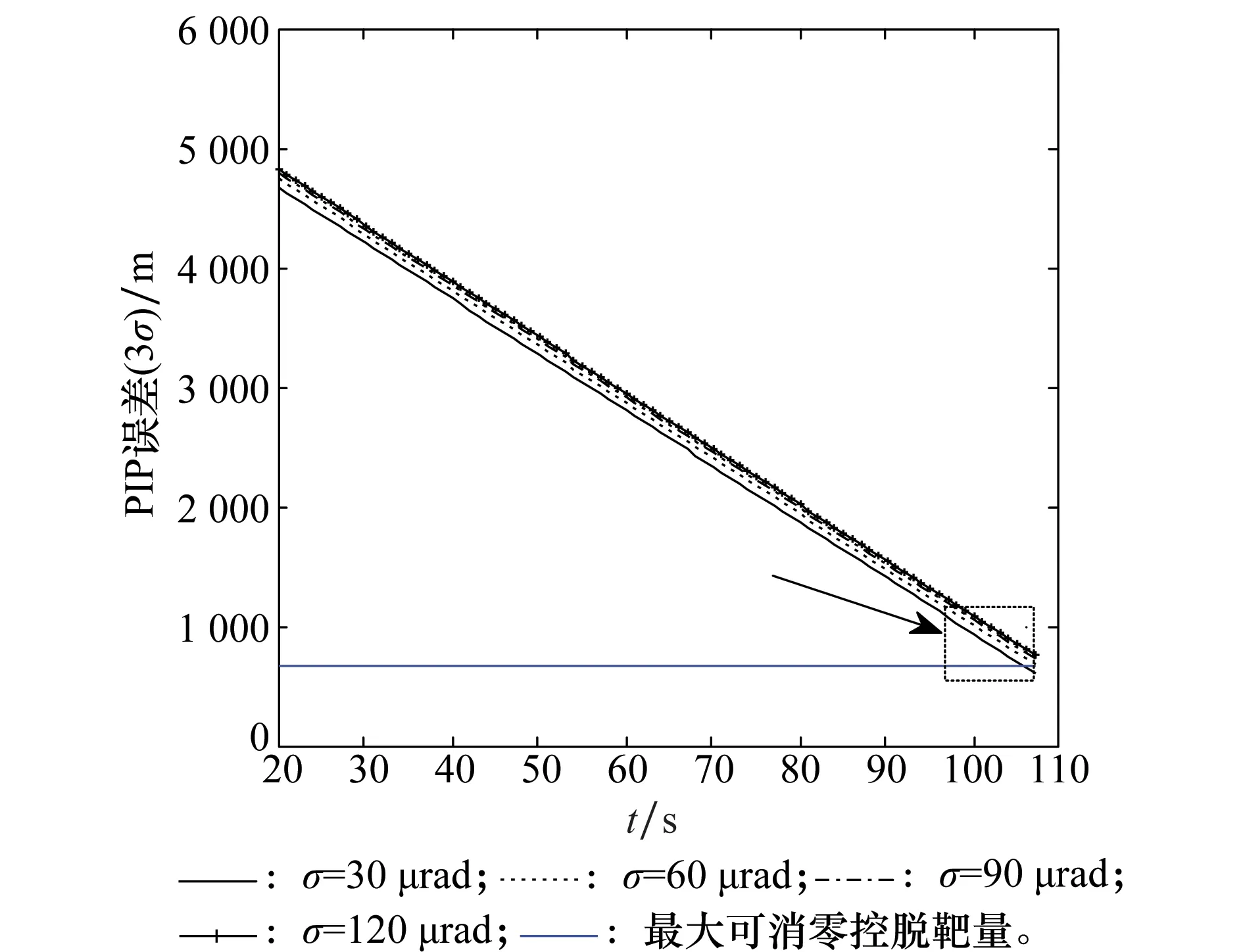
圖6 視線角度誤差對PIP誤差的影響Fig.6 Effect of angle measurement error on PIP error

(2) 采樣頻率對PIP誤差的影響

保持觀測角誤差σLOS=60 μrad不變,從圖7可以看出隨著采樣周期的減小,每時刻PIP的精度會逐漸降低。相比于觀測誤差對PIP精度的影響,采樣周期對PIP的影響更大,主要是因為觀測誤差只影響位置跟蹤精度而采樣周期不僅影響位置跟蹤精度還會影響速度跟蹤精度。

4.3 攔截彈修正能力對衛星跟蹤能力需求

保持采樣精度T=2 s不變,當觀測角誤差為30 μrad、60 μrad、90 μrad、120 μrad時,中段修正所需總的轉移速度均為181.7 m/s,小于攔截彈攔截器所能提供的最大轉移速度,滿足中段機動需求。從圖6可以看出當觀測角誤差為60 μrad、90 μrad、120μrad時,中段結束時刻PIP誤差大于末段最大可消除脫靶量,不滿足中末段交接條件,當測角誤差為30 μrad時,中段結束時刻PIP誤差小于末段最大可消零控脫靶量,滿足中末交接班的條件。要實現成功攔截,要同時滿足中段及末段的機動需求,因此當采樣周期為2 s時,觀測誤差為30 μrad時才能實現成功攔截,觀測誤差為60 μrad、90 μrad、120μrad時不能實現成功攔截。

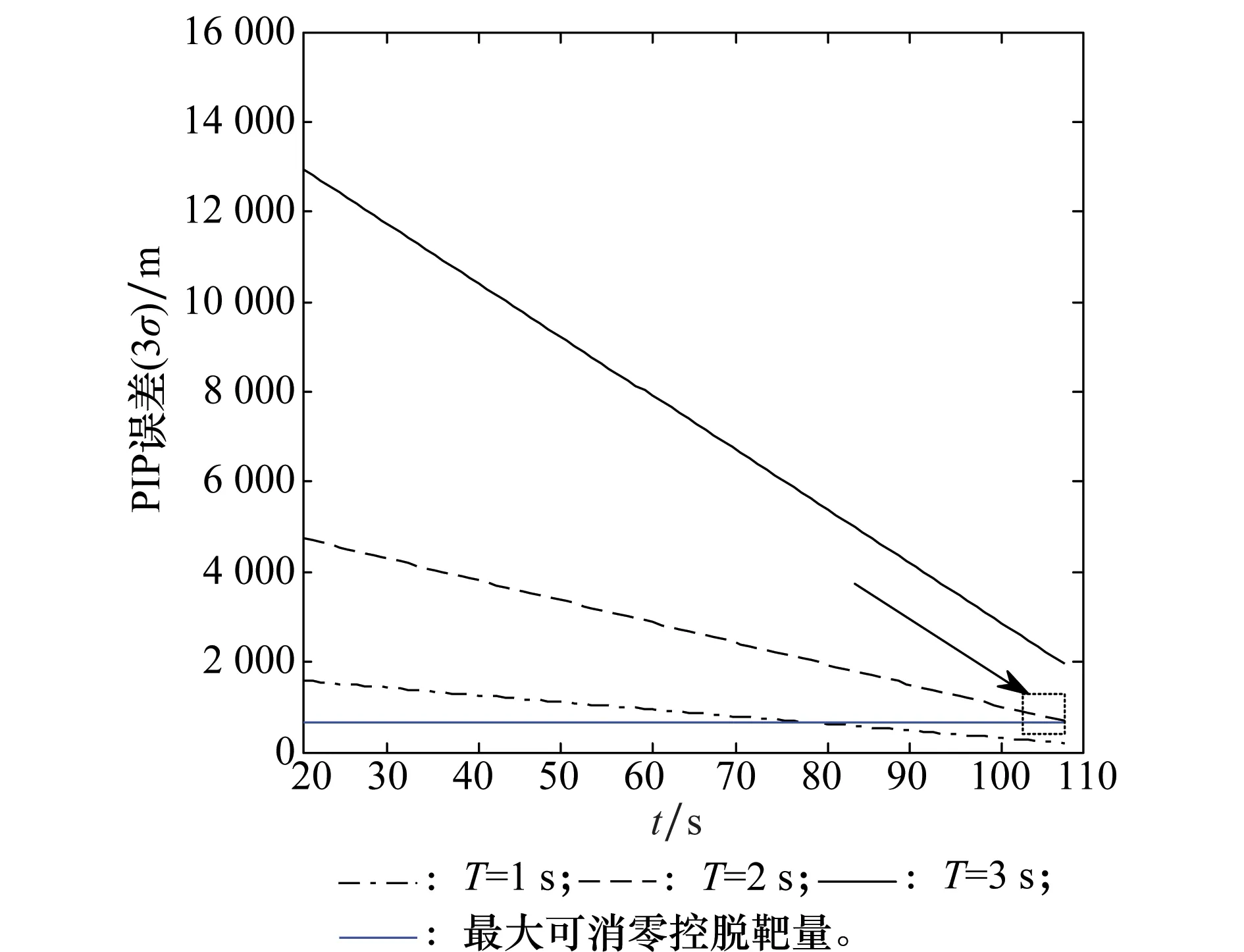
圖7 采樣周期對PIP誤差的影響Fig.7 Effect of measurement period on PIP error

保持觀測角誤差σLOS=60 μrad不變,當采樣周期為1 s、2 s時,中段修正所需總的轉移速度分別為62 m/s和181.7 m/s,小于攔截彈攔截器所能提供的最大轉移速度,滿足中段機動需求。當采樣周期為4 s時,中段修正所需總的轉移速度為495.2 m/s,大于攔截彈攔截器所能提供的最大轉移速度,不滿足中段機動需求。從圖7可以看出當采樣周期為2 s、4 s時,中段結束時刻PIP誤差大于末段最大可消除脫靶量,不滿足中末段交接條件,當采樣周期為1 s時,中段結束時刻PIP誤差小于末段最大可消零控脫靶量,滿足中末交接班的條件。因此,當觀測誤差為60 μrad時,采樣周期達到1 s時才能實現成功攔截,采樣周期為2 s、4 s時不能實現成功攔截。

結合圖6與圖7可知,攔截彈中段修正所需總的轉移速度和中末段交接時刻PIP誤差大小與LEO衛星的采樣周期和測角誤差密切相關,將采樣周期設為1 s、2 s、4 s,測角誤差設為30 μrad、60 μrad、90 μrad、120 μrad,分析不同組合條件下利用衛星跟蹤信息引導攔截彈攔截目標是否滿足中末段機動能力需求,結果如表2所示。

采樣周期和觀測角度誤差是LEO衛星的重要技術指標,攔截器的中末段機動能力決定了LEO衛星的技術指標要求。從表2中可以看出影響中段總轉移速度的主要是衛星觀測的采樣周期,因為影響中段轉移速度的主要因素是速度跟蹤PCRLB,而速度跟蹤PCRLB不受觀測角度誤差的影響而只受采樣周期的影響。因為速度和位置PCRLB都會影響末段初始PIP誤差,所以衛星觀測角度誤差和采樣周期都會影響末段初始PIP誤差。表2中給出了滿足中末段機動需求的LEO衛星的采樣周期與觀測誤差的組合。

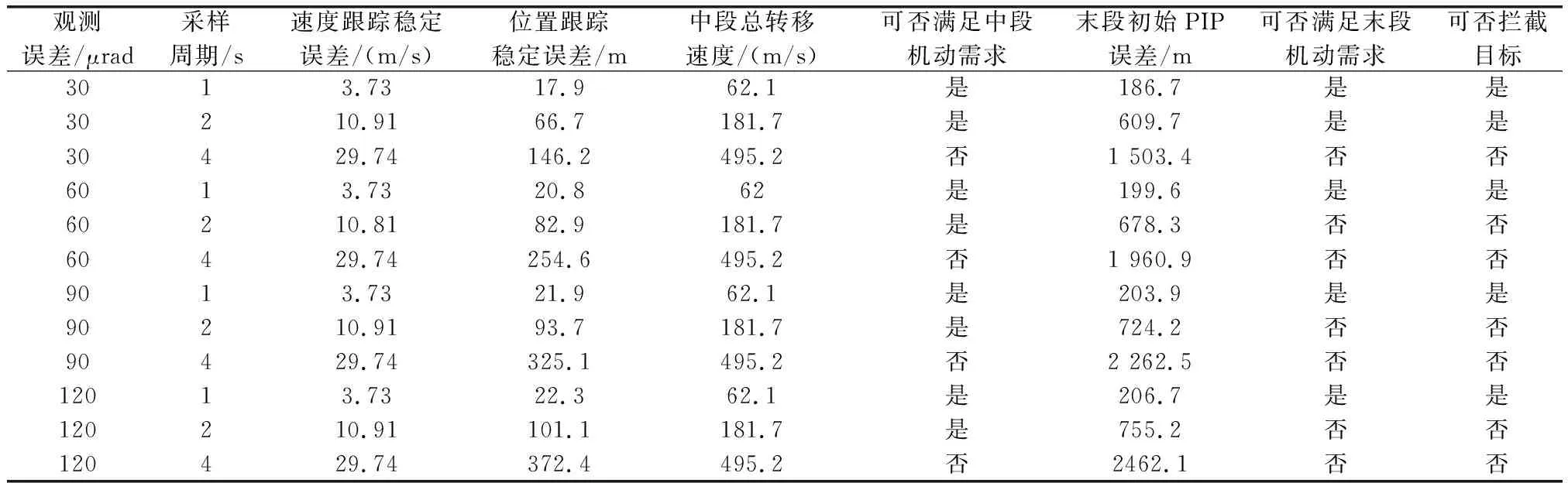
表2 LEO衛星信息引導下攔截彈中末段機動需求滿足情況

5 結 論

本文以PCRLB為指標衡量LEO衛星的探測能力,分析了觀測角誤差和采樣周期對LEO衛星速度和位置跟蹤能力的影響,建立了攔截系統的PIP及其精度計算方法,分析了衛星觀測角度誤差和采樣頻率對PIP誤差的影響,進而分析不同采樣周期和觀測誤差組合下利用LEO衛星引導攔截彈時是否滿足中末段的機動需求,給出了成功攔截時的LEO衛星技術指標要求。本文將反導防御系統中探測系統的探測能力與攔截系統的需求綜合分析,從攔截系統修正能力需求的角度研究衛星的跟蹤能力將對LEO衛星系統建設提供重要指導。