大型公交站的動態排隊論分析與優化

劉 偉，陳科全，謝忠金

(重慶交通大學 交通運輸學院，重慶 400074)

0 引 言

城市交通系統作為城市發展的重要基礎支撐體系，運行效率高低對城市發展、運作和擴展等方面起著重要的作用。然而機動車的迅猛增長，使得人們逐漸意識到無節制的私家車使用帶來后果的嚴重性，公交優先發展已成為緩解交通擁堵、治理交通問題的重要舉措。地面常規公交的通行能力是衡量公交運行效率的重要指標，通行能力包括了車行道和公交站臺內。即便公交在車行道的行駛時間較多，但在某些中間站，由于線路集中、客流量大以及周邊交通運行狀況較差，會使得站內延誤情況嚴重，甚至會蔓延到主路干擾交通流。同時不精確和不恰當的研究方法會忽略問題的嚴重性。因此對于公交站臺的這一現象值得研究。

城市中心區常見港灣式公交站臺，國內外大量的文獻主要從擬定設置站臺的通行能力來分析站臺內的線路容量[1-4]，大部分集中在對BRT站臺的研究[5-6]，鄭曉峰等[7]針對性的分析了BRT下，站臺乘客誘導問題，提出了誘導均衡模型，對于誘導方案的生成有重要意義，但應用載體有限，隨著站臺數量增加，精度越低。目前國內并沒有普及BRT情況下，對于常規公交站臺的研究文獻較為缺乏。在現階段的研究中，排隊論模型作為研究站臺內的延誤情況、排隊情況和通行能力的一個重要理論[8-10]，但對于排隊論模型中的參數設定與實際情況有一定差別。因此通過分析港灣式站臺內乘客候車行為和公交站內運行的交通行為，將排隊論模型中的服務時間設定為動態函數。從時空的角度出發，在站臺模擬時設置了平峰和高峰參數，在此基礎上提出了主、副站臺以及智能引導模式。最后構建了多服務臺下動態狀態參數的排隊論模型，對比分析了站臺在優化前后的平均排隊長度以及通行效率等指標。

1 站內公交運行和乘客候車特性

1.1 站內公交車運行特征分析

常規公交停靠站可分為直線式和港灣式，由于港灣式站臺存在公交車輛與旁側的社會車輛分流和合流現象，常會因為進出公交站造成的延誤或者旁側車流量大而導致以站臺為中心的周邊區域運行效率低。從公交車在站內運行特性的角度分析，造成站內延誤的原因如下：

1)公交車進站后，激進型駕駛員停靠時，強行加塞導致隨后車輛停靠困難。

2)公交車不按規定停靠在指定位置，甚至會出現車輛占用港灣式站臺內的行車道上下乘客的情況。

3)公交車出站時，由于1、2的共同作用，使得服務完的公交車與加塞車輛和不規范停靠車輛發生沖突，進而難以出站。

4)駕駛員進站時不了解站內停靠位空閑信息，具有盲目性。

1.2 站內乘客的候車特性分析

港灣式公交站能容納較多公交線路停靠，常修建于公交線路密集的區域，候車乘客較多。在站內常見乘客來回跑動，客流交織情況頻發。引起這一現象的主要原因是由于公交車停靠位置與乘客所站位置有一定差異。

2 基于動態服務時間的排隊論模型

2.1 排隊模型基本參數意義

從整體研究公交停靠站的運行方式：各條線路的車輛依次進入站臺，上下乘客后駛出站臺。因此將站臺看作服務臺，而公交的停靠時間則看作服務時間，站臺、公交車和乘客構成一個排隊系統，見圖10。

圖1 公交站內排隊模型Fig. 1 Queuing model of bus station

為了考察現狀某站臺實際運行情況下的排隊和延誤情況，以及站臺優化后的運行情況。筆者建立了基于狀態改變的排隊論模型，其中各個參數的物理意義如下：

1)公交達到：中間站每條線路的發車頻率可認為是無相關性，設定每條線路到達某站的規律服從參數為λ(>0)的泊松分布。

(1)

式中：Pi表示站臺內第i條線路公交車的到達頻率，(veh·h-1)；n表示站內公交線路的總數。則單位時間內達到k個車輛的概率為

(2)

考慮到平峰和高峰時，道路上的交通狀況會影響公交車到站的頻率，因此將公交車達到規律分為兩個層次：平峰和高峰。采用Minkowski距離中的歐式距離對高峰數據聚類分析:

(3)

式中：d2(pi,y)表示所有點的歐氏距離向量組；pi表示需分析點的原始坐標；yk表示被聚類分析點的坐標。

2)排隊規則：常規的排隊規則分為先到先服務、后到先服務、隨機服務和優先服務，但對于港灣式公交站而言，排隊規則可分為兩種情況：當車輛較少時，排隊規則為先到先服務，而且有多個服務臺；當車輛較多時，站內可能會發生車輛超車搶先進行服務的情況。

2.2 動態服務時間參數意義

目前對于公交在站內服務時間的研究主要以公交車上、下乘客的時間作為排隊系統中的服務時間，但相對于實際情況而言，服務時間應包括為公交車進站到停靠的時間t1，公交車上、下乘客時間t2，公交車起步到駛出站臺的時間t3。因此服務時間T為

T=t1+t2+t3

(4)

根據公交站內公交車的行駛特性，可以發現公交站在高峰期時，公交車在站內的服務時間由于司機的駕駛行為、站內無秩序情況和多次停車等因素發生變化，因此上述的t1，t2，t3，均為理想狀況下的服務時間。

為了使得模型中的參數與實際情況符合度更大，對服務時間設定動態參數α。通過分析公交車到達后的排隊規則發現：當公交站內飽和程度未達到閾值χ時，服務時間與理想狀態下相符：當公交站內飽和程度超過閾值χ時，服務時間可通過非線性函數f(si)標定：

(5)

式中：si表示某時刻站內的實際車輛數；i表示服務臺個數；閾值χ需根據實際站臺調查數據標定。

根據上述分析，服務率有兩種情況，其分布函數G(t)：

(6)

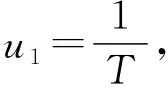
2.3 優化服務系統參數的物理意義

2.3.1 單服務系統下的評價參數設定

實際情況下，港灣式公交站可看作動態服務時間下，單服務臺的M/M/1/N排隊系統。這種情況下，系統達到穩定分布狀態時，有以下評價參數計算：

1)平均排隊長度Tp

(7)

2)公交通過站臺的平均時間Ws

(8)

2.3.2 多服務臺下引導方式及評價參數設置

為了提高站臺的運行效率，通過分析行人和駕駛員的特性，筆者建議對站臺進行分區管理，設置主、副站臺，按照線路到達的頻率以及上下車人數分配到兩個站臺，站臺示意圖以及站內運行方式如圖2：

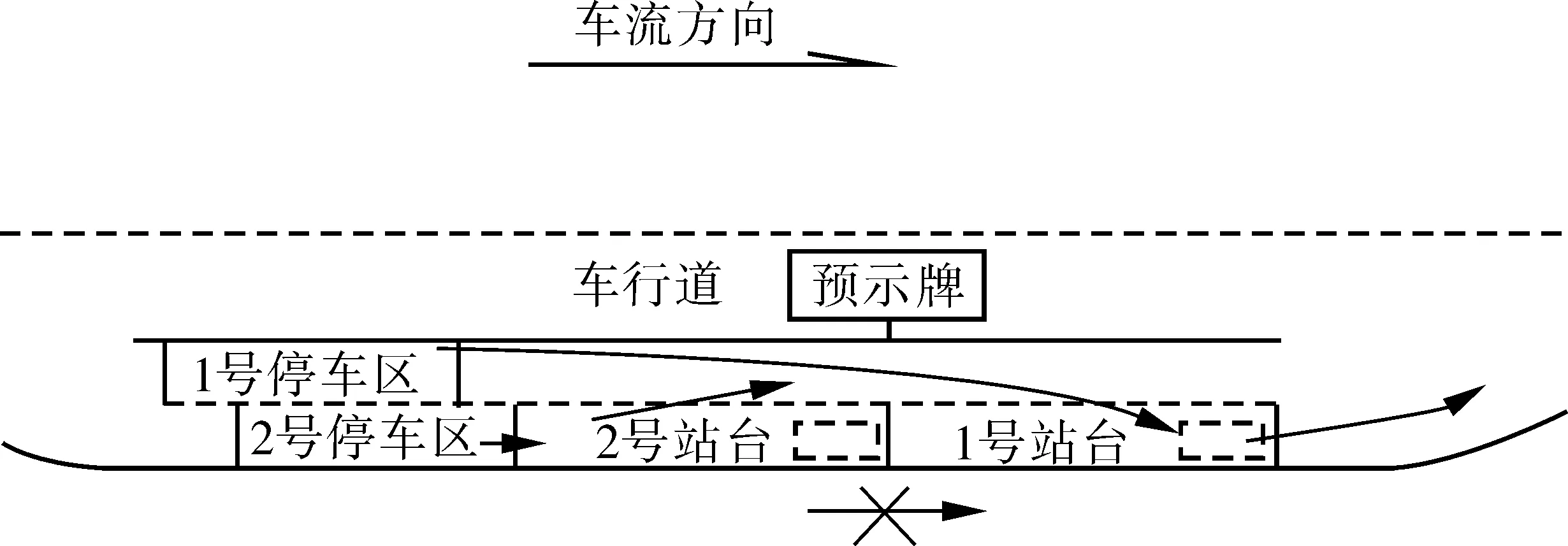
圖2 停車位及運行規則示意Fig. 2 Sketch map for parking and operation rules

圖2所示的站臺為設置主、副站臺以及其附帶停車位的站臺示意圖，其中預示牌會根據主、副站臺設置的地磁線圈采集的信息提示公交車站臺內部是否有空余停車位，如果沒有，則提示在停車區等待。公交站運行模式為M/M/2/N的排隊系統，該系統運行條件為：站臺的停車區的容量大于等待服務的公交車輛數量，排隊是消散的；由于存在主、副站臺，因此港灣式站內部車道數不少于2條；不考慮主線道路的交通流對公交車進出站的影響。

當優化后系統達到穩定分布狀態時，可用以下評價參數：

1)平均等待概率c(s,p)

平衡狀態下系統中顧客數為n的概率，即當n>p時，隨后到來的車輛必須排隊等候，p表示站臺的實際容量。由Erlang等待公式可得系統需要等待的平均概率c(s,p)：

(9)

式中：s表示服務臺數量，在文中僅有主、副站臺，因此s=2；ρ=ρs，且s取1；p0表示站臺空閑時的概率，ρs表示在s個服務臺情況下的服務強度，計算公式如式(10)、式(11)：

(10)

(11)

2)平均排隊長度Lp

排隊長度為衡量優化效果的關鍵因素之一。進行優化后，不會存在站內車輛數超過容量的情況，因此對主副站臺的si有一定限制，si∈(0，p)，其計算公式為

(12)

3) 公交通過站臺的平均時間Wy

(13)

式中：Ly=平均排隊長度(Lp)+正在接受服務的顧客平均數(ρ)。

3 實例應用

將基于狀態改變的排隊論模型以及優化設計應用到實際中，可以對模型進行檢驗，同時也能對實際站臺的優化效果進行觀測，筆者以重慶市江北區大廟站為例進行分析說明。

3.1 站臺背景分析以及參數標定

大廟站位于重慶市觀音橋商業區和紅旗河溝輕軌站的中間，客流密集，旁邊為雙向六車道。該站臺為港灣式站臺，全長100 m，泊位數為9個，有39條線路停靠此站，經觀察該站旁側交通流運行穩定，但站臺內經常出現擁堵情況。根據視頻調查數據分析，各延誤情況見表1。

1)公交車強行插隊導致擁堵，這種情況主要發生在高峰時期，發生次數占總延誤次數的28.5%，但是延誤時間卻是最高的，占總運行時間的21.5%。

2)公交車的二次以及多次停靠，主要由于乘客在站內的分布分散，導致公交車要多次停車，發生次數占總延誤次數的5.8%，次數雖然少，但由于再次停靠需要減速和加速，導致延誤時間占總運行時間的9.2%。

3)由于行人的分布分散，但車輛不會二次停車，而是由于斷續客流而造成的停靠過久。

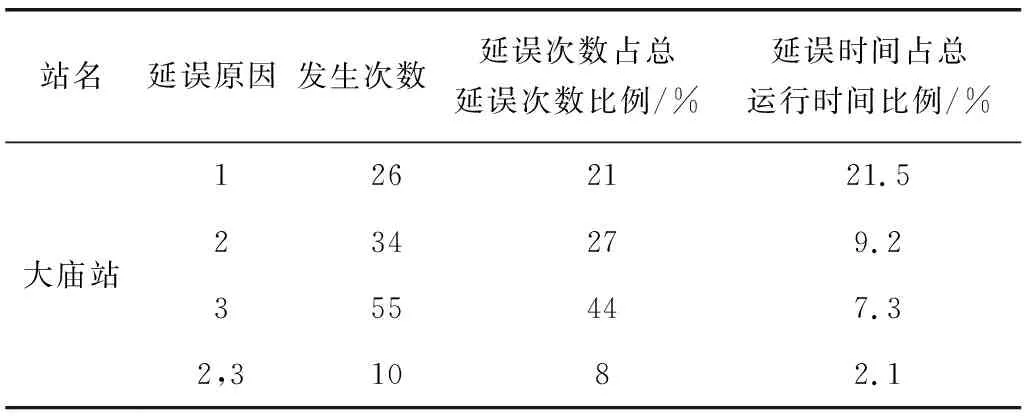
表1 現狀下大廟公交站總體延誤情況Table 1 The overall delay of Damiao bus station under the currentsituation

注：延誤原因：1.相鄰公交車強行加塞；2.公交車在站內多次停靠；3.由于乘客的斷斷續續上車，公交車停靠過久。

圖3為公交車達到頻率的部分調查數據，調查時間段為15:00-19:00，包括了平峰和高峰，從圖中可以發現數據具有明顯的分層性，采用歐式距離對數據聚類分析得到表2：

圖3 公交平峰-高峰到達率Fig. 3 Bus arrival rate in normal times and rush hour

時間分類平峰高峰公交到達率/(veh·min-1)0.2280.155

為了標定狀態改變下排隊論模型中的參數χ，對大廟站中實際的t1，t2，t3進行了調查，整理數據如圖4。圖4中x軸用連續數字替代公交線路，數據表明公交在站內停靠時間相對于進出站所需的時間很小。通過視頻數據發現，隨著站內車輛數增多，車輛通過站臺的時間增大，考慮到服務時間不僅包括了排隊時間(t1)還包括了進站和出站時間(t2，t3)，改進排隊論模型中的非線性服務時間函數f(si)如圖5：

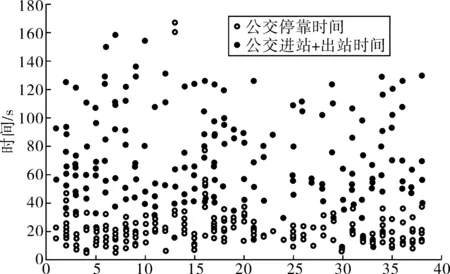
圖4 不同線路停靠時間與進出站時間Fig. 4 Docking time as well as import and exit time of different lines

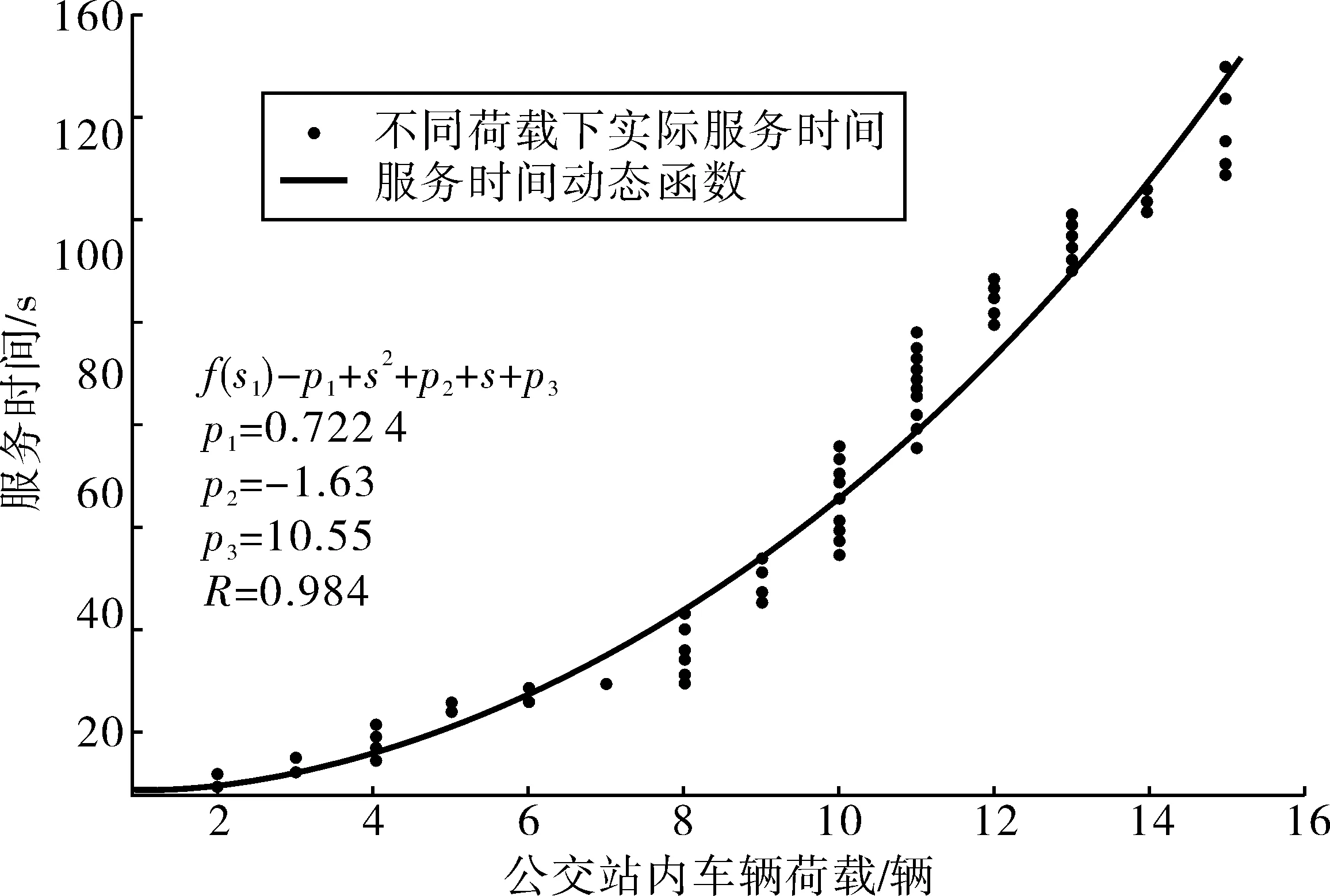
圖5 服務時間動態函數Fig. 5 Dynamic function of service time

3.2 計算結果對比分析

對大廟站調查數據處理分析以及模型中參數的標定，帶入計算公式(7)～式(12)以10 s為時間間隔對模型進行計算分析，結果如表3：

表3 公交站優化前后對比Table 3 Comparison of bus station before and after optimization

根據計算結果可以得到以下結論：

1)站臺內公交車輛無秩序的運行會導致在高峰時期站內延誤嚴重，而行人的候車特性則會加重這個問題，使得在高峰時期站內的平均排隊車輛數多達5輛，采用引導模式后，能夠解決這一問題，在高峰時期能夠降低77.5%的排隊情況，且平均排隊只有1.25輛，不會出現車輛排隊到旁側車道的情況，優化效果明顯。

2)多服務臺引導模式下，上下車客流交織和乘客的跑動情況會明顯減少。根據計算結果發現：平峰和高峰時，公交車通過一個站臺的平均時間分別降低了26.3%和41.1%。主要是由于優化后的運行模式使得主副站臺的實際容量均在5輛以下，從而最大服務時間的上限服從均值為20.46 s，方差為4.2的正態分布。

4 結 語

以港灣式站臺內乘客候車特性和公交進站出站行為為研究基礎，綜合了客流、延誤類型、時間和發車間隔等因素，分析了現有研究存在的問題以及影響模型精確的參數，建立了動態服務時間下排隊論系統，并提出了多服務臺下的引導方式。實例表明：在大型港灣式站臺內，平峰和高峰應采用不同的研究參數，特別是服務時間會因為站內存在的車輛數不同，呈現出相應的非線性函數關系。優化后的運行模式，能夠提高公交車通過站臺的運行效率，并規范站臺內的運行秩序。在隨后的研究需要考慮主線交通流對公交進出站造成一定影響的情況，優化效果的波動性，同時如果能夠結合站內先進的信息采集和公交車的GPS數據，能夠進一步優化站內的運行規則，提高通過時間。