大型核電機組冷卻劑屏蔽主泵動態模型及響應特性研究*

趙語，劉滌塵，王力，趙潔，林毅，雷勇

(1. 武漢大學 電氣工程學院，武漢 430072； 2.國網福建省電力有限公司經濟技術研究院，福州350012)

0 引 言

主泵是核電廠冷卻劑系統中唯一的旋轉設備，主要用于熱量傳遞和余熱導出，其可靠性直接影響到反應堆的安全運行，屬于核安全1級[1-2]。先進壓水堆核電機組采用單級、全密封、離心式屏蔽泵，由于其飛輪和電動機轉子一起包容在冷卻劑系統的承壓部件內，使其徑向尺寸受到極大限制，相比于其他堆型，具有更小的轉動慣量，秦山一期冷卻劑泵轉動慣量為1 750 kg·m2，秦山二期M310機組轉動慣量為5 210 kg·m2, 以AP1000為代表第三代先進壓水堆核電機組冷卻劑屏蔽泵轉動慣量僅為969 kg·m2，因此對系統電壓頻率波動更為敏感[3-5]。

現有文獻對冷卻劑主泵模型及響應特性作了較多研究。文獻[6]詳細介紹了冷卻劑主泵瞬態特性和斷電下計算模型，基于四象限特性模型來描述泵的運轉特性。文獻[7]根據冷卻劑主泵轉矩平衡關系結合四象限特性曲線提出了系統流量特性曲線的計算模型，可用于冷卻劑主泵斷電事故惰轉工況的分析。文獻[8]等采用轉矩平衡關系對冷卻劑主泵斷電后惰轉轉速模型進行了簡化計算，并與其他轉速模型進行比較，認為新的轉速模型更符合實際情況。文獻[9]針對冷卻劑主泵斷電惰轉工程中的瞬態水力特性進行試驗研究，并采用四次多項式擬合惰轉過程的流量、轉速隨時間變化。這些模型主要從泵的水工力學角度考慮，參數難以獲取，同時主要考慮惰轉模型工況下模型，難以接入電力系統分析。文獻[10]等在忽略主泵摩擦轉矩基礎上，提出了適用于電力系統分析冷卻劑主泵模型，該模型主要針對轉動慣量較大的二代模型。

本文針對第三代核電機組冷卻劑主泵所采用屏蔽電機的特性，考慮摩擦阻力矩，建立適用于電力系統分析的冷卻劑主泵動態模型，采用實驗與辨識相結合方法獲取模型參數，仿真對比分析了冷卻劑主泵的動態響應。在核電并網仿真系統中，仿真分析了電網擾動對主泵及核反應堆的影響。

1 冷卻劑主泵動態建模

適用于電力系統分析的冷卻劑主泵模型，要求主泵參數明確，準確反映實時反映電網側和冷卻劑能量交換過程，建立冷卻劑主泵模型的關鍵是建立主泵電磁轉矩和阻力矩模型。

1.1 冷卻劑主泵瞬態轉子運動方程

根據動量守恒搭建冷卻劑主泵瞬態轉子運動方程：

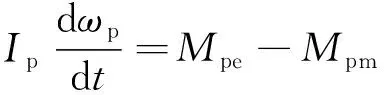
(1)

式中Ip為轉子轉動慣量；ωp為主泵轉子角速度；Mpe為電磁力矩；Mpm為總阻力矩，包含水力扭矩和機械摩擦轉矩。

屏蔽冷卻劑主泵因其飛輪和轉子固封于承壓部件內，使得其轉子轉動慣量小于非屏蔽冷卻劑主泵[11]。轉速對轉矩變化靈敏度高，摩擦轉矩不可忽略，因此屏蔽冷卻劑主泵的阻力矩應同時計及水力阻矩Mp1和由于機械摩擦造成的摩擦阻力矩Mp2，即有:

Mpm=Mp1+Mp2

(2)

Mp2表示主泵機械摩擦引起的阻力矩，摩擦力矩的大小與轉速有關，同時也與泵的固有特性有關，難以精確計算，此處引入經驗公式[6]表示為：

(3)

式中K3為常數；n由泵的實驗值確定， 一般根據經驗值取1.7～2.4。

1.2 轉矩模型

電磁轉矩模型主要是建立電磁轉矩與廠用電電壓和頻率關系，理論推導建立屏蔽電機電動機電磁轉矩模型，表示為：

(4)

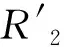
(5)

式中U1*，f1*分別為實際電網電壓和頻率；K1，K2為與冷卻劑主泵相關的常系數。

建模過程中忽略冷卻劑流量分布特點，則冷卻劑質量流量可以表示為：

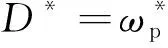
(6)

式中D*為冷卻劑質量流量標幺值；ωp*為轉子角速度標幺值。

1.3 核電機組反應堆及熱力系統模型

將搭建的冷卻劑主泵動態模型，按照圖1所示核電機組反應堆及熱力系統模型圖[12-13]，建立核電機組反應堆及熱力系統模型，其中反應堆及其熱力系統數學模型為：

(7)

選用圖1和式(7)中：Nr為堆芯中子通量；β為緩發中子份額；λ為緩發中子延時常數；Rext為控制棒感生的反應性；TF為燃料溫度；Tcav為反應堆中冷卻劑的平均溫度；Tavg為冷卻劑系統平均溫度；Tc1為反應堆冷卻劑入口；Tc2為反應堆冷卻劑出口溫度；THL為冷卻劑蒸汽發生器一次側入口溫度；TCL分別冷卻劑蒸汽發生器一次側出口溫度；hs為蒸汽發生器二次側出口蒸汽比焓；D*為冷卻劑管道冷卻劑質量流量標幺值；UL和fL為電網側主泵供電電壓和頻率；Ps為主蒸汽壓力。

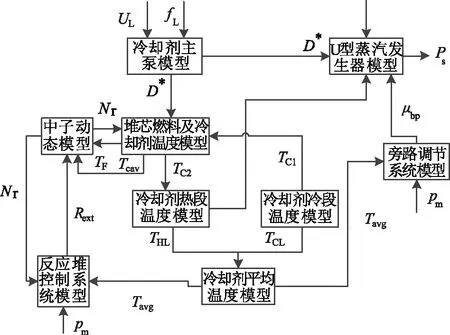
圖1 核電機組反應堆及熱力系統模型圖

2 冷卻劑主泵模型校驗與分析

選實際投產運行的核電機組因為設計、實際運行狀態等，導致不同機組參數也會存在不一致情況，針對此，采用智能參數識別方法針對對應機組的試驗數據進行參數識別，確立相關參數值，進而進行仿真運算。根據圖2所示主泵運算框圖，在MATLAB/Simulink中搭建相應仿真軟件，利用MATLAB/Simulink參數識別工具箱根據已有實驗數據對相應模型進行參數辨識，主辨識參數包括電磁轉矩常系數K1、K2;摩擦轉矩常系數K3、n,其余參數均采用設計參數。

圖2 冷卻劑主泵運算框圖

對一機組實驗數據進行仿真分析，辨識出系數

K1=244.115 2,K2=3 056.8,K3=0.061 7,n=2.12。

針對搭建的模型及參數識別結果，建立完整的屏蔽電機冷卻劑泵模型進行仿真，并與文獻[8,10]中模型進行比較分析，驗證模型的準確性。三種模型主要特點為：

模型1：為本文搭建模型，考慮摩擦轉矩可以進行冷卻劑主泵惰轉分析和電網波動主泵動態響應分析；

模型2：文獻[8]中模型，將摩擦轉矩等效為水力阻矩比例，可以進行冷卻劑泵惰轉分析；

模型3：文獻[10]中模型，忽略摩擦轉矩，可以進行冷卻劑主泵惰轉分析和電網波動主泵動態響應分析。

2.1 惰轉工況下各種模型對比分析

冷卻劑主泵惰轉是反應堆冷卻劑系統流量下降的重要工況[14]，也是核電廠安全分析和核電廠主泵設計的重要參照。

對某一機組，采用不同模型仿真的主泵惰轉響應如圖3和表1所示。

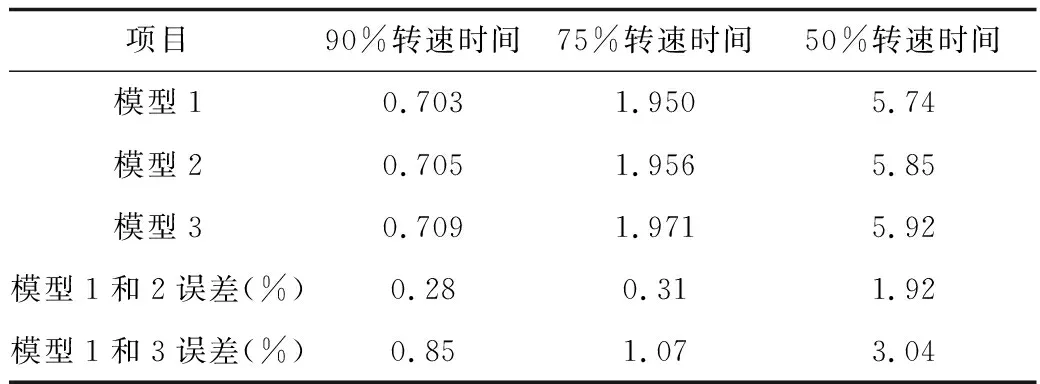
表1 三種不同模型惰轉比較

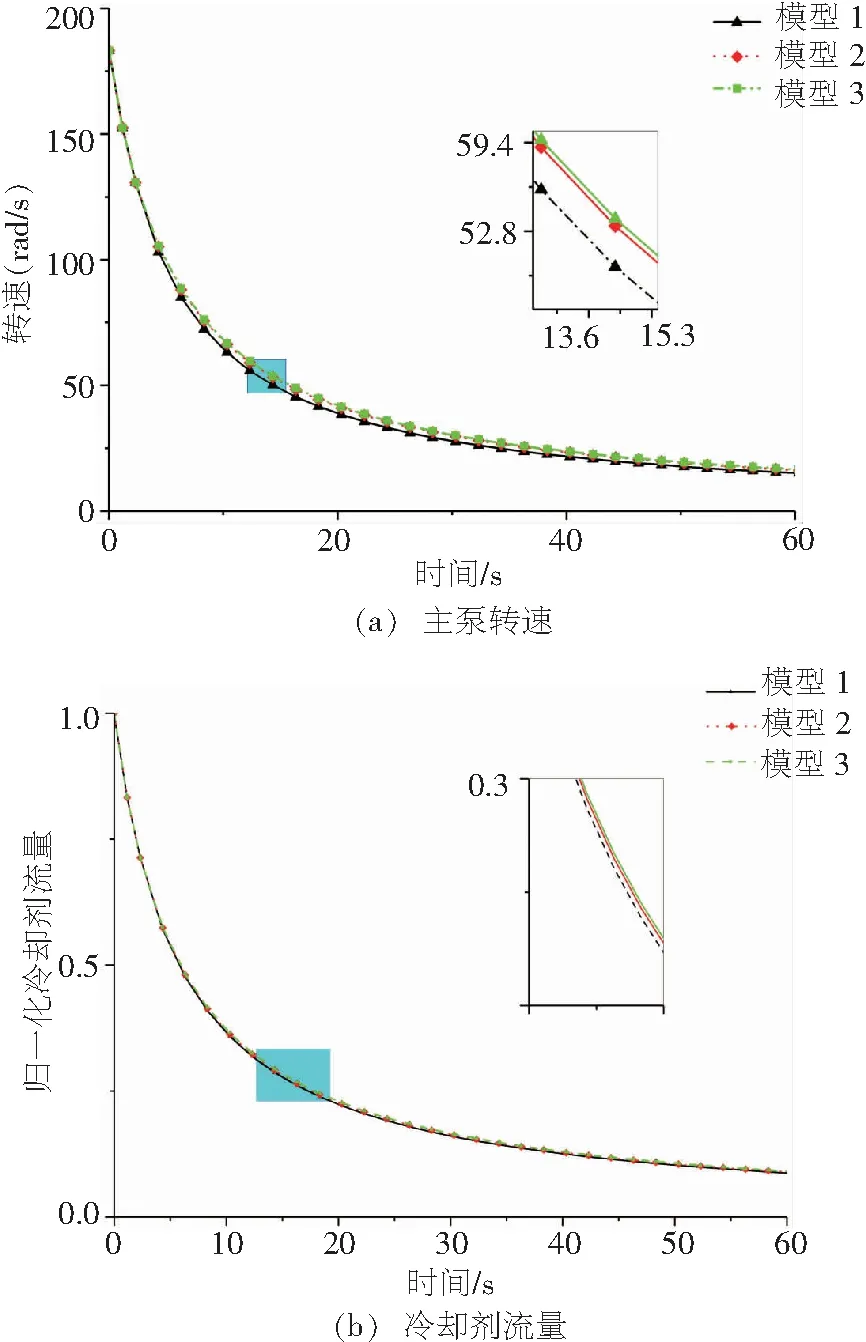
圖3 惰轉工況下模型對比分析

由圖3可知：

(1)三種不同主泵模型仿真的惰轉曲線有差異，但差別不大;

(2)因模型2引入了常系數摩擦轉矩，所以模型2相比于模型3模擬轉速下降速度較快;

(3)模型1與模型2相比，轉速下降速度較快，這是由于該機組由實際試驗數據辨識的摩擦轉矩大于模型2中的制定的確定的摩擦轉矩，對圖3(b)冷卻劑流量分析可以看到相同的結果;

(4)三種模型下主泵惰轉的半流量時間有較大差別，最大偏差達到3.04%。因此，是否考慮摩擦轉矩，對惰轉半流量時間有較為明顯的影響;

(5)對于實際運行的不同機組，僅以確定的冪函數描述摩擦轉矩與轉子角速度的關系是不準確的，根據實際運行試驗數據擬合確定二者關系，可以提高模型的準確性。

2.2 電壓波動時冷卻劑主泵響應仿真分析

在t=0 s時，如果主泵供電電壓發生圖4(a)所示的擾動，主泵轉速和冷卻劑流量響應如圖4所示。

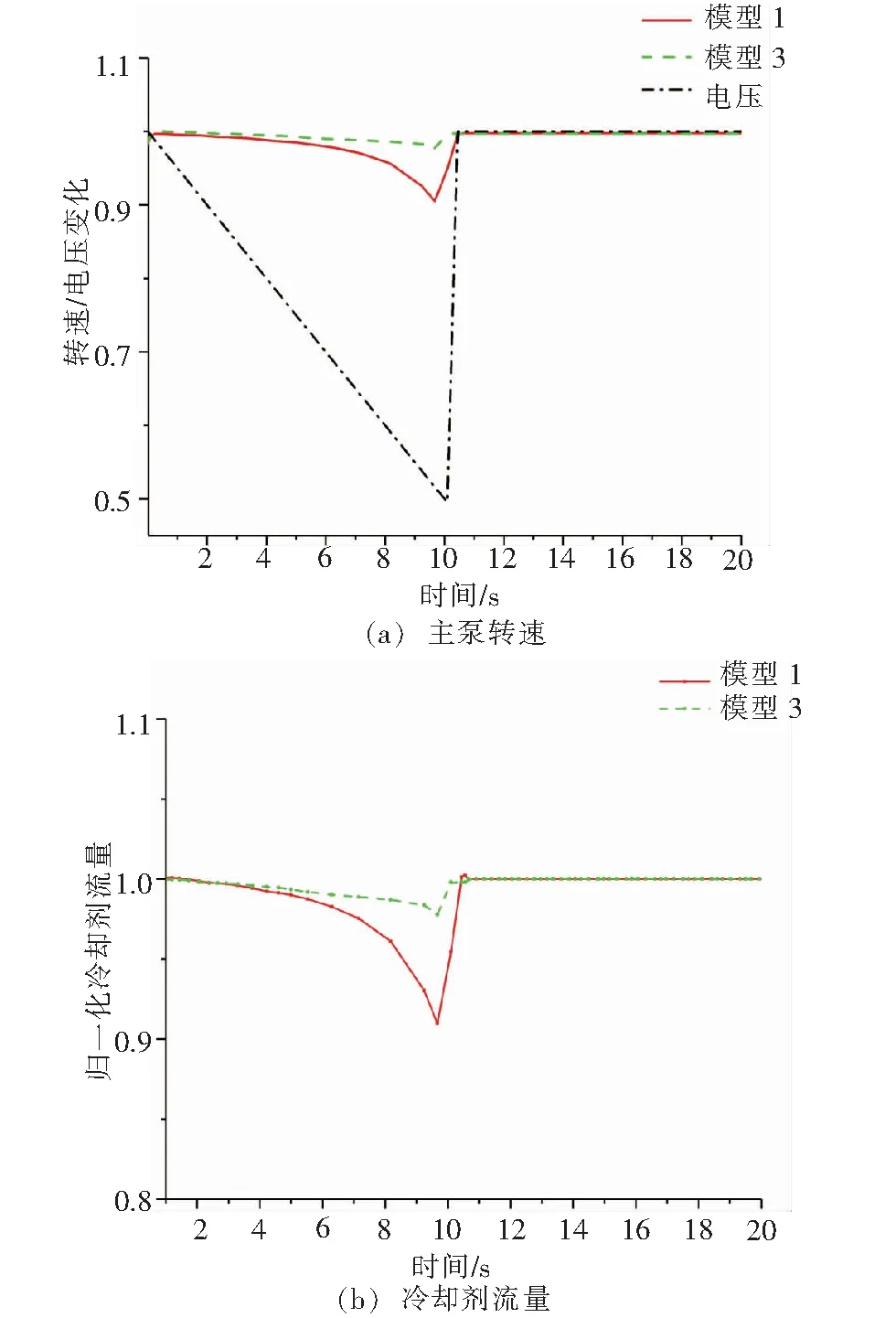
圖4 電壓波動時冷卻劑主泵動態響應

由圖4可以看出，由于摩擦轉矩的影響，在電壓下降時，模型1仿真的轉速和冷卻劑流量的下降速度明顯大于模型3；在電壓恢復階段，模型3仿真的轉速和冷卻劑流量恢復時間大于模型1，模型1更符合實際。

2.3 頻率波動時主泵響應仿真分析

在t=2 s時，如果主泵供電頻率發生圖5(a)所示的擾動，主泵轉速和冷卻劑流量響應如圖5所示。

由圖5可以看出，在頻率下降時，模型1轉速和冷卻劑流量與模型3下滑速率基本一致，模型1最低點小于模型3；在頻率恢復時，模型3仿真的轉速和冷卻劑流量恢復時間大于模型1。

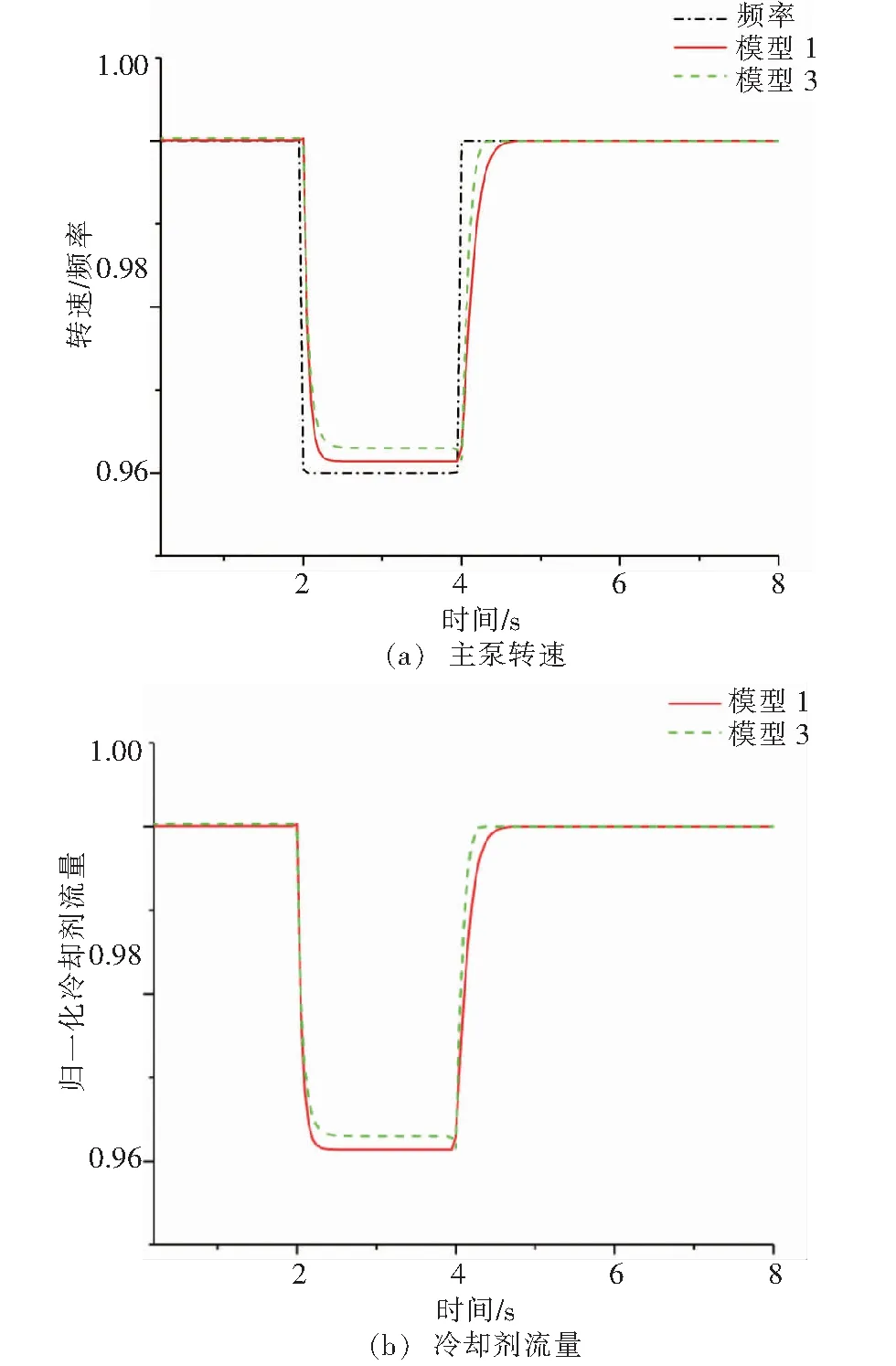
圖5 頻率波動時冷卻劑主泵動態響應

實際電網故障中，頻率和電壓波動一般為同時發生。在t=2 s時，主泵供電側發生非金屬短路，t=2.1 s時故障切除，主泵響應仿真如圖6所示。

由圖6可知：

(1)t=2.0 s，電網側發生故障時，電壓迅速降低

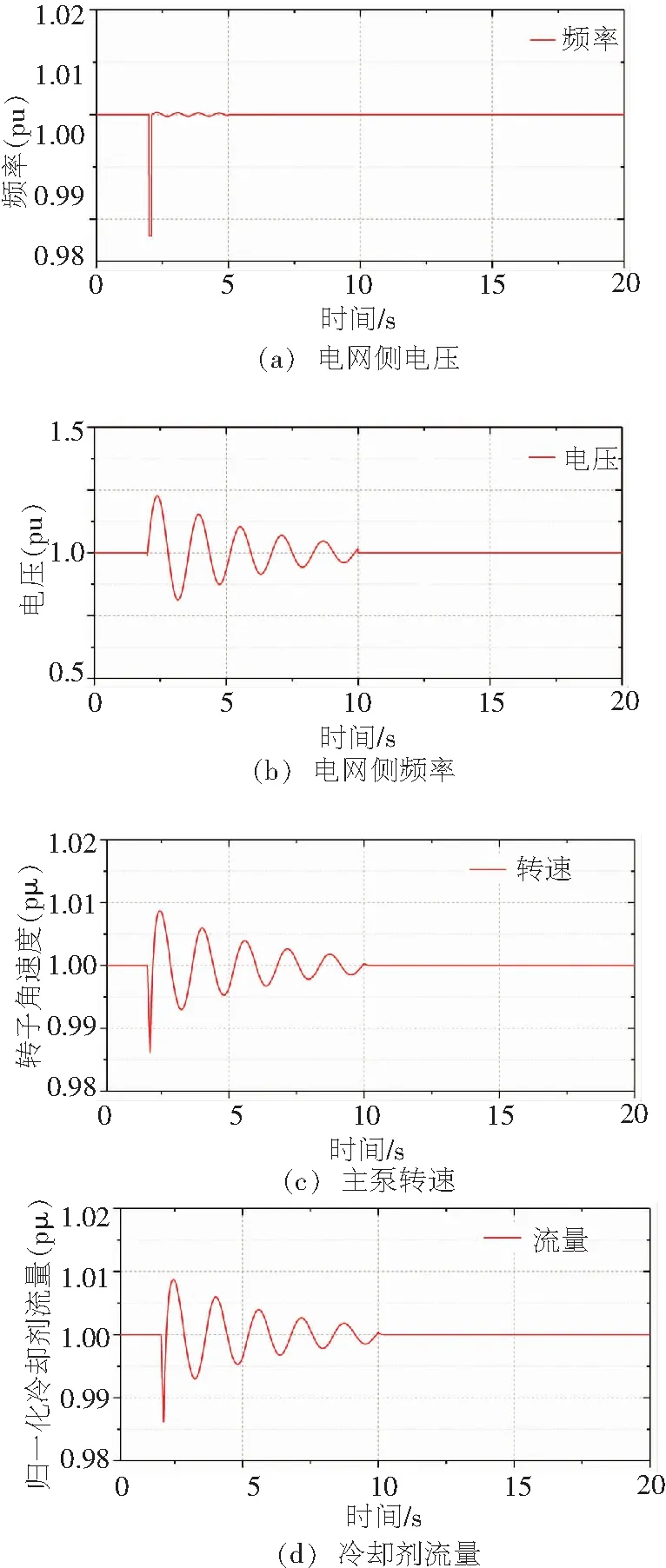
圖6 頻率/電壓波動冷卻劑流量對比曲線

至0.45 pu，故障迅速切除后，頻率發生最高振幅為1.01 pu的振蕩恢復，電壓迅速恢復;

(2)t=2.0 s～2.1 s,主泵轉速和冷卻劑流量可認為是電壓和頻率波動共同作用，最大偏差為0.013 pu;

(3)t=2.1 s后，電壓迅速恢復，主泵轉速和冷卻劑流量依然存在很大的波動，這是由于頻率波動造成的,最大偏差為0.009 pu;

(4) 對比(3)和(4)可知，在電壓明顯波動，而頻率波動不明顯時，頻率波動造成的主泵轉速和冷卻劑流量偏差依然占主要因素，說明電網側對核電的影響，主要是頻率波動造成的影響。

3 模型的應用分析

將模型1接入已有的核電機組模型[12]，并接入電力系統仿真軟件進行全時域仿真，可以實時得到在電網側故障時，核電側的冷卻劑流量，堆芯燃料溫度等輸出，進而根據結果作用于核電廠運行分析等。

若在t=2 s時電網側頻率階躍下降到0.98 pu，0.96 pu時，主泵及反應堆響應如圖7所示。從圖7中可以看出，當頻率下降時，冷卻劑流量迅速降低到某數值，同時冷卻劑與反應堆堆芯燃料熱交換降低，堆芯燃料溫度上升，此時蒸汽壓力降低，中子通量上升。

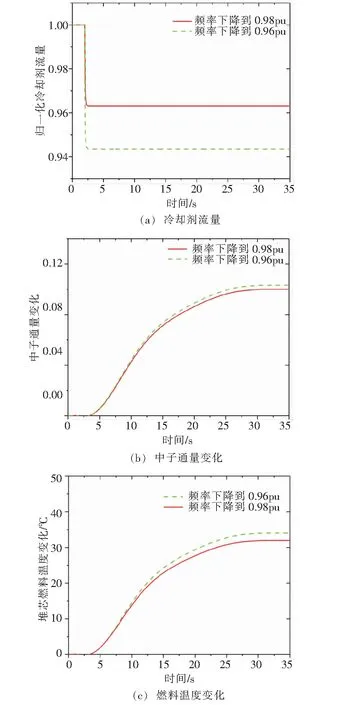
圖7 主泵和反應堆響應

4 結束語

本文研究建立了大型核電機組冷卻劑屏蔽主泵動態模型，仿真研究了其響應特性，并得到以下結論：

(1)相比于常規軸密封泵，屏蔽主泵轉動慣量較小，因此其對電壓、頻率動更敏感；

(2)摩擦轉矩對屏蔽主泵半流量惰轉時間有較明顯影響，在屏蔽主泵建模時應予以考慮，不可忽略，應根據實際運行試驗數據擬合確定摩擦轉矩與轉子角速度的關系，以提高模型的準確性；

(3)頻率擾動對主泵轉速、流量的影響比電壓擾動更明顯，在運行中應提高廠用電供電質量，重視核電機組擾動對廠用電頻率的影響。