基于沖擊電壓下電纜等效電阻值的絕緣狀態評估新方法

李巍巍，甘德剛，朱軻，劉鳳蓮，何珉，周凱

(1. 國網四川電力科學研究院， 成都 610072； 2.四川大學 電氣信息學院， 成都 610065)

0 引 言

交聯聚乙烯(XLPE)電力電纜因其優異的電氣性能而被廣泛應用于城市輸配電網絡中[1-2]。相關研究表明，電力電纜的故障率與時間為一浴盆曲線，一般使用壽命約30年。而早期投入運行的電纜，隨著時間的增加，有可能發生絕緣故障，導致可靠性下降。此外，電纜的安裝并非十分規范，受實際規劃的限制，電纜的共溝率往往較高，一旦發生絕緣故障，極易引發連鎖反應，造成大面積的停電事故。所以，準確評估電纜的絕緣狀態成為保證供電可靠性的關鍵。

國內外對電力電纜絕緣狀態的評估進行了大量研究。包括直流疊加法[3]、交流疊加法[4]、低頻疊加法[5]、tan δ法[6]、極化-去極化法[7-8]等。上述方法施加電壓均不高，而某些缺陷在低電壓下無法暴露，卻極有可能在操作或雷電等過電壓情況下突然發生絕緣事故。因此，如果能得到過電壓下的電壓和電流與電纜絕緣之間的關系，從而評估電纜絕緣的狀態，可能會對缺陷的診斷更為準確。而國內在此方面的研究較為缺乏，大部分都是基于穩態電壓下的絕緣狀態評估，幾乎沒有基于過電壓的絕緣狀態評估研究。國外有利用沖擊電壓對電纜絕緣狀態進行評估，主要利用傳遞函數和電介質光學介電譜[9]，以及沖擊電壓下的頻率響應[10-11]。提出了電力電纜的3元件等效電路模型[12]、4元件等效電路模型[13]和多元件串聯的等效電路模型[14-17]，用于時域反射法對水樹進行定位，并未用于電力電纜絕緣狀態的評估。

文章基于多元件串聯模型，搭建了短電纜的多RC的串并聯等效電路，理論分析了電力電纜的各層及整體等效電路參數的計算公式和推導方法，提出了一種基于沖擊電壓下電纜等效電阻值計算和絕緣狀態評估的新方法，并通過理論推導和仿真計算進行了驗證。

1 原理分析

1.1 電纜的等效電路模型

為了利用等效電路的參數值對電纜的絕緣狀態進行評估，本文選取型號為YJLV22-8.7/15-3*95的XLPE電力電纜為研究對象，進行等效電路模型的建立。圖1為剝除外護套和鎧甲的單芯電力電纜的橫截面圖，其結構包括導體、內半導電層、XLPE層、外半導電層和銅屏蔽層。

圖1 XLPE電纜樣本的橫截面

由于水樹缺陷的出現，會導致電力電纜絕緣的下降。基于此，建立了如圖2所示的無水樹電纜的等效電路模型，如圖3所示的有水樹電纜的等效電路模型。由于文中的研究對象是短電纜，所以在等效電路模型中忽略了短電纜的導體及銅屏蔽層的電阻和電感。

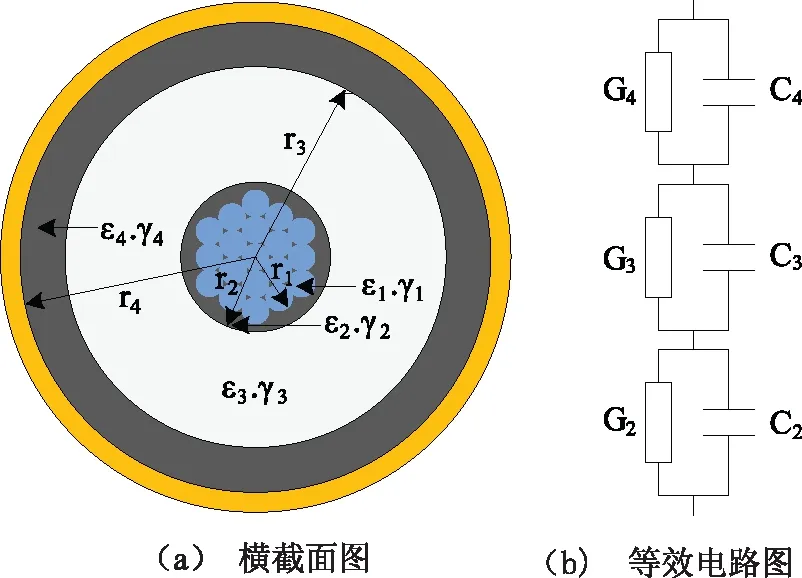
圖2 無水樹電纜模型

如圖2(a)所示的橫截面中，εi和γi(i=1～4)分別為第i層的相對介電常數和電導率。如圖2(b)所示的等效電路中，G2和C2分別為內半導電層的電導和電容；G3和C3分別為XLPE絕緣層的電導和電容；G4和C4分別為外半導電層的電導和電容。

圖3 有水樹電纜模型

如圖3(a)所示的橫截面中，將水樹區域等效為一夾角為α的扇形，εw和γw分別為水樹部分的相對介電常數和電導率。如圖3(b)所示的等效電路中，G31和C31分別為XLPE絕緣層半徑介于r2和r31環狀無水樹區域的電導和電容；G32和C32分別為XLPE絕緣層半徑介于r31和r3之間，夾角為π-α環狀無水樹區域的電導和電容；Gw和Cw分別為XLPE絕緣層半徑介于r31和r3之間，夾角為α扇形有水樹區域的電導和電容。

1.2 電纜的等效電路參數

為了分析有、無水樹電纜的等效電路參數值的區別，以及對電纜絕緣狀態的影響。本文基于電路理論公式推導長度為L電纜的等效電路參數。其中各層及整體的電導值為[18]：

(1)

式中Gi(i=2～4)分別為第i層的電導,ri(i=1～4)分別為第i層的半徑。

(2)

式中Gs為多層電導的串聯總電導。

則無水樹和有水樹電纜的電導分別為：

(3)

(4)

同理可得，電纜各層及整體的電容值為：

(5)

式中Ci(i=2～4)分別為第i層的電容，ri(i=1～4)分別為第i層的半徑。

(6)

式中Cs為多層電導的串聯總電導。

(7)

(8)

通過比較式(3)和式(4)，可以得出有水樹電纜的電導比無水樹的大，即有水樹電纜的等效電阻小于無水樹電纜，絕緣水平較低；比較式(7)和式(8)，有水樹電纜的電容比無水樹的大。而實際電纜中有水樹部分電纜占整段電纜長度比重很小，如若將每段電纜視為RC并聯模型，整段電纜就由多個RC并聯模型組成。整體等效電阻受水樹部分的等效電阻影響較大，即影響著電纜的絕緣狀態。

2 評估方法及理論證明

水樹的存在將使得電纜等效電路參數的等效電阻值變小，而實際中水樹的存在會使得電纜的絕緣強度降低，即等效電阻值與絕緣狀態存在同向變化的相關性。所以在上述RC并聯等效電路模型的基礎上，施加沖擊電壓u(t)于電纜上，利用電纜上的沖擊電壓u(t)及對應的沖擊電流i(t)，提出一種新的方法評估電纜的絕緣狀態。首先，從能量的角度，定義有功損耗為：

(9)

沖擊電壓u(t)下的沖擊電流i(t)為：

(10)

將式(10)代入式(9)得：

(11)

因為u(0)=0，u(∞)=0，所以：

(12)

(13)

式中R為短電纜的整體等效電阻；C為短電纜的整體電容；W為有功損耗。

由式(13)可得電阻值為：

(14)

通過式(14)可得到電纜等效電路中等效電阻值，從而可以通過它對電纜的絕緣狀態進行評估。其依據應為等效電阻值越大，即絕緣性能越好，反之亦然。對實際電纜進行評估時，可通過橫向和縱向比較的方法對電纜絕緣性能進行評判。將新電纜的初始等效電阻值作為基準，在后續測試中將電纜的等效電阻值與基準值相比較。如若沒有新電纜的初始等效電阻值，可對比同一批次或同一線路的三相電纜的等效電阻值[19]。如果需要確切的數值，也可以通過成熟的評估方法進行驗證，得出合適的評判標準[20]。

3 結果與分析

為了驗證電纜等效電阻值的理論計算公式的正確性，利用ATP模擬不同電阻值的電纜參數進行仿真，基于式(14)通過MATLAB計算得到等效電阻值，并對比仿真設置的電阻值與計算所得等效電阻值。

建立短電纜RC并聯等效電路模型，并加入了沖擊電壓發生器的等效電路，整體的電路原理圖如圖4所示。通過設置不同的電阻、電容值，模擬不同長度和不同絕緣狀態的電纜。實測10 cm長的短電纜電容值在40 pF～70 pF之間，電阻值為GΩ級。因此，選取電容值分別為50 pF和100 pF，電阻值分別為0.1 GΩ、1 GΩ、10 GΩ、100 GΩ進行仿真。

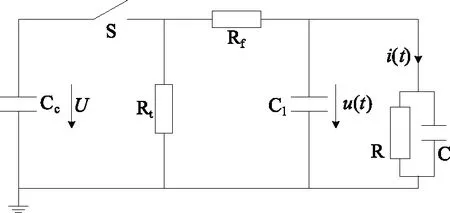
圖4 仿真電路圖

仿真得到如圖5所示的沖擊電壓波形和沖擊電流波形。

圖5 沖擊電壓和沖擊電流波形

從圖5可以得出，沖擊電壓與沖擊電流的起始時刻相同，且起始和終止值均為零，無工頻電壓與電流的角度差。沖擊電流波形不同于沖擊電壓波形，沖擊電流波形的前面部分為正，后面部分為負；沖擊電流峰值時間位于沖擊電壓峰值時間的前面，沖擊電壓峰值時間位于沖擊電流過零時間的前面。

利用式(14)計算不同仿真數據結果，得到沖擊電壓下不同等效電阻值計算結果。其中表1為仿真電容值為50 pF時，不同仿真電阻值和計算等效電阻值的數據；表2為仿真電容值為100 pF時，不同仿真電阻值和計算等效電阻值的數據。

表1 50 pF電容時電纜的電阻值

表2 100 pF電容時電纜的電阻值

從表1和表2可以得出，不同電容值時，仿真設置的電阻值與理論計算的等效電阻值之間誤差最大為0.4%。即基于沖擊電壓下電纜等效電阻值的計算方法是可行的，能夠作為評估電纜絕緣狀態的一種新的方法。

4 結束語

文章通過建立電力電纜的RC串并聯等效電路模型，給出了電力電纜各層及整體的等效電路參數，提出了一種基于沖擊電壓下電纜等效電阻值的計算方法，理論推導出了其計算公式，并得出利用等效電阻值的大小評估電纜絕緣狀態的新方法。仿真計算結果表明，該計算方法所得等效電阻值的結果與仿真設置電阻值之間的誤差小于0.4%，在誤差的可接受范圍內，表明該方法是可行的。