基于VMD和柔性形態學的輸電線路故障測距方法
陳惠,莫付江,許夢素,汪培培
(江蘇大學 電氣信息工程學院,江蘇 鎮江 212013)
0 引 言
對于電力系統來說,輸電線路故障測距是十分重要的一部分。當發生線路故障后,傳統人工巡線方式比較浪費時間和精力,高效、快速的故障定位可以及時發現故障位置,從而迅速排除故障,及時恢復供電,維護了電網的安全,減少了社會經濟損失[1],所以研究輸電線路故障測距具有很重要的現實意義。
故障測距有故障分析法和行波法,故障分析法的精度不高,然而行波的定位精度高,所以現在行波檢測成為了熱點。干擾會對信號的檢測帶來困難[2-4]。因此為了提高檢測精度,需要對含噪的信號先進行降噪處理,目前降噪和行波檢測方法主要有小波變換(WT)[5-6]和希爾伯特-黃變換(HHT)[7]兩種,但這些方法還存在一定的局限性。小波模極大值法雖然對故障信號奇異性檢測有良好的效果,但是小波變換需要選取適合特定信號的小波基函數和分解尺度,不能達到需要的滿意效果。HHT方法中的EMD分解效果容易受到包絡方式影響,會出現端點效應、模態混疊等問題。
變分模態分解(VMD)是這幾年新出來的一種自適應信號分解方法,分解模態穩定性好,能夠更好地反應信號的奇異性特征。柔性形態學是基于積分幾何和隨機集論建立起來的一種非線性數學方法,使用柔性形態腐蝕、膨脹的不同結合,有效去除干擾的同時可以在時域快速得到突變點時刻。將VMD與柔性形態學結合起來,在有效去除噪聲的基礎上還進一步的放大了信號突變點,實現故障行波波頭的有效定位。
1 變分模態分解[8-10]
變分模態分解是一種最新的完全非遞歸的信號分解方法,尤其是對采樣和噪聲處理更強大,對于一系列人工和真實數據,我們可以達到預期的實際分解結果。VMD的目標是一個輸入信號剖分成多個離散的子信號(模式)uk, 每個子信號K是主要環繞著一個確定跟隨分解的中心脈動wk。該方法與EMD所使用的循環篩分剝離的信號處理方法有差別,采用迭代尋找變分模型最優解來確定每個模態的頻率中心及帶寬。
第一步:變分問題目標函數的構建
(1)使用Hilbert變換來計算每個模式相關的分析信號獲得一個單邊的頻譜;
(2)將每個模態的頻譜轉換為“基帶”,通過與一個指數混合調整到各自預估的中心頻率;
(3)帶寬現在是通過解調信號的H1高斯平滑來估計,即方L2-范數的梯度,由此產生的約束變分問題如下:
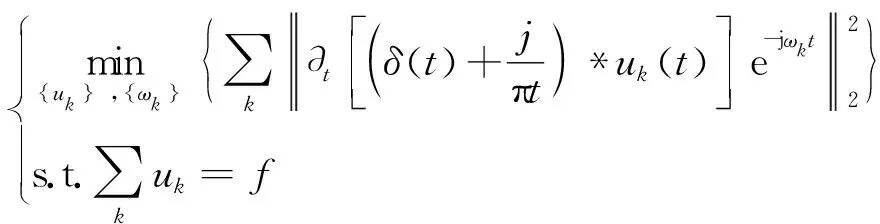
(1)
式中{uk}={u1,…,uk}和{wk}={w1,…,wk}分別表示所有模態的集合和他們的中心頻率。
第二步:使用二次懲罰項和Lagrange乘子算法將問題變為非約束性變分問題,這兩個組合受益于有限權下二次型懲罰的收斂性和拉格朗日乘子約束的嚴格執行。因此,我們引入了擴充的拉格朗日如下:
L({uk},{ωk},λ)=
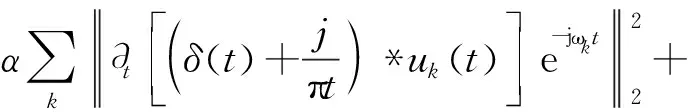
(2)
式中λ(t) 為Lagrange乘法算子;α為數據保真約束的平衡參數。

VMD的完整算法流程如下:
(1)初始化{uk1},{wk1},λ1,n=0;
(2)n=n+1,執行循環;
(3)根據式(3)更新uk,根據式(4)更新wk;
(3)
(4)
(4)k=k+1,重復步驟(3),直至k=K結束;
(5)根據式(5)來更新λ。
(5)
(6)判斷是否滿足式(6)。
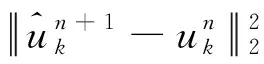
(6)
若是條件滿足則迭代停止,否則跳轉到步驟(2)。
2 柔性形態學[11]
柔性形態學由數學形態學擴展、演變而來,其構造元素由核心和邊界兩部分組成,采取的是加權統計排序的方式,與數學形態學相比,魯棒性更好,抑制干擾的能力更強。柔性形態學是假設結構元素[B,A,r]包含參數A,B和r,A,B?Z2,A?B,r為重復度,1≤r≤|B|,|B|是B的基數。集合A為硬核,集合B為構造元,B/A為柔性邊界。
柔性形態學的腐蝕和柔性膨脹可定義如下:
[f(b):b∈(B/A)n]}
(7)
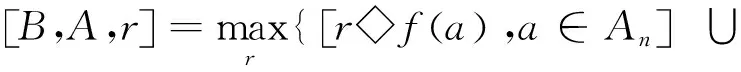
[f(b):b∈(B/A)n]}
(8)
式中◇表示重復操作符;Θ和⊕分別表示腐蝕和膨脹運算符。
柔性形態學的開運算和閉運算可定義如下:
(f·[B,A,r])(n)=(fΘ[B,A,r])⊕[B,A,r](n)
(9)
(f·[B,A,r])(n)=(f⊕[B,A,r])Θ[B,A,r](n)
(10)
式中° 和·分別表示開運算和閉運算。
2.1 平均柔性形態濾波器[12]
形態開運算是先腐蝕后膨脹,對信號起到平滑作用,可以去除突出部分;形態閉運算是先膨脹后腐蝕,能夠平滑信號輪廓,消除小洞,因此可通過結合形態開運算和形態閉運算來構造濾波器。但是開運算會使信號濾出結果偏小,閉運算濾出結果偏大,采用平均柔性形態學濾波器可以避免這些影響:
(11)
2.2 柔性形態邊緣檢測[13]
經典的邊緣檢測方式對噪聲比較敏銳,所以抗噪性就比較差,反而會在邊緣檢測時加強了噪聲,這里使用式(12)將信號膨脹結果與信號開運算結果做差值,即能夠抑制噪聲又能夠保存邊緣突變點特征信息。
g(n)=(f⊕[B,A,r]-f°[B,A,r])(n)
(12)
g(n)是邊緣檢測的結果,選擇軟閾值方法設定輸出閾值,這樣更能突出信號特征。噪聲強度為:
(13)
則輸出閾值為:
(14)
柔性形態邊緣檢測的結果:
(15)
3 仿真分析
本文在PSCAD/EMTDC仿真軟件中搭建了一個220 kV的輸電線路仿真模型,如圖1所示。
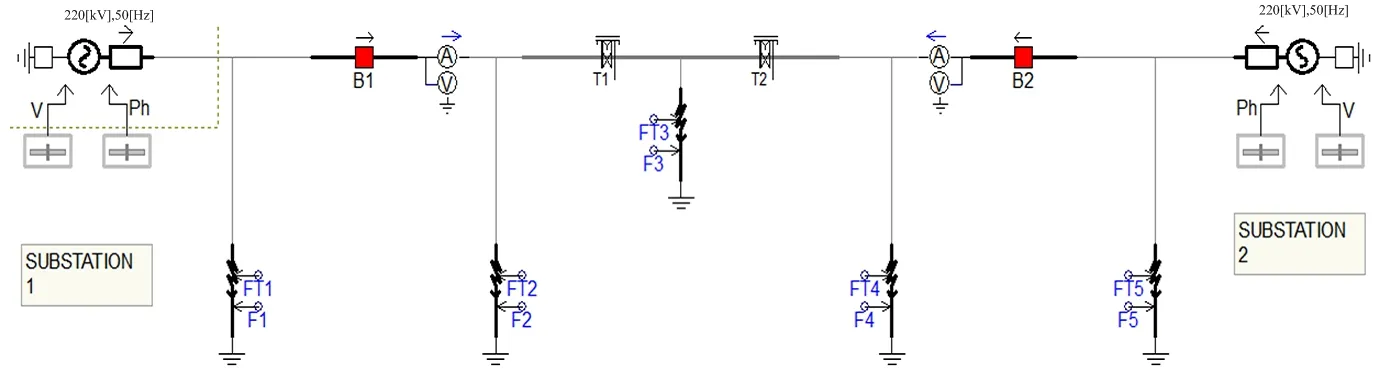
圖1 220 kV輸電線路仿真模型
輸電線路全長20 km,采樣頻率為1 MHz,故障點分別設在距離M端30 km、70 km、100 km、140 km、和180 km,0.2 s時發生故障,取故障后3 ms的數據分析。以距離M點30 km發生A相接地短路為例,先使用凱倫貝爾變換將取得的數據處理得到電壓的線模分量,使用VMD方法分解(K=3,α=2 000),再使用平均柔性形態濾波器對IMF1分量進行剩余噪聲的去噪,最后使用柔性形態邊緣檢測對突變點信息特征進行提取,獲得故障行波波頭時刻。
輸電線路M、N側的電壓線模分量如圖2、圖3所示。電壓線模分量經VMD進行分解,自適應的濾去了一部分的干擾,得到了三個模態,其中模態IMF1最能體現原信號的特征。M、N兩端VMD分解得到的模態分量IMF1如圖4、圖5所示。
使用平均柔性形態濾波器對剩余干擾去除得到的IMF1如圖6、圖7所示。

圖2 M側的電壓線模分量
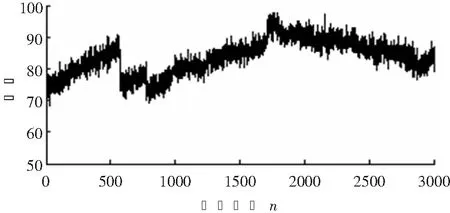
圖3 N側的電壓線模分量

圖4 M側的模態分量IMF1
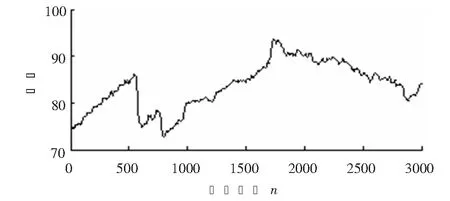
圖5 N側的模態分量IMF1
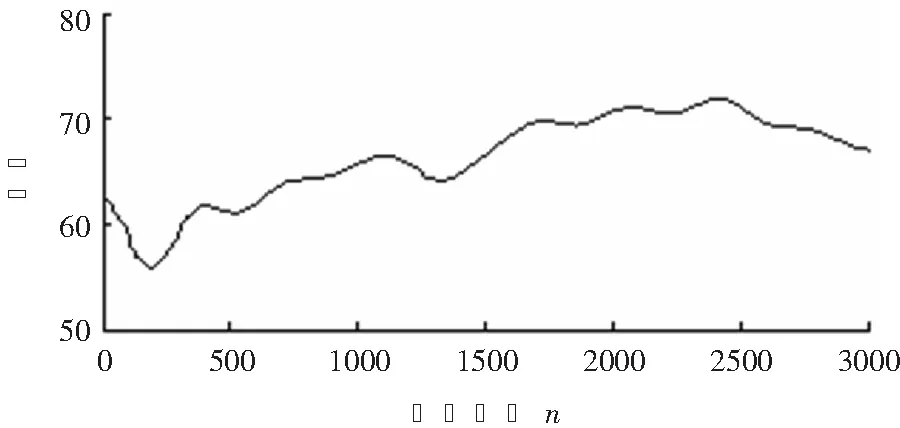
圖6 M側濾波后的IMF1

圖7 N側濾波后的IMF1
由文獻[14]可知一種新的雙端測距新算法
(16)
式中L是線路的水平長度;tM,tN分別是故障行波從發生時刻到達M、N兩端的時間。
對濾波后的IMF1進行柔性形態邊緣檢測,在減少噪聲影響的同時還保留了突變點信息,準確識別出突變點位置,圖8是柔性形態邊緣檢測結果,從圖中可知:tM=102,tN=571,代入式(16)即可得到測距結果。
在不同故障點位置的情況下進行了測量分析,測距結果如表1所示。
表1數據表明此方法對于不同故障距離中的不同故障類型都能進行精確的故障測距,測距誤差在允許的范圍之內,并且故障點距離線路中央越近,故障測距的準確度就越高。

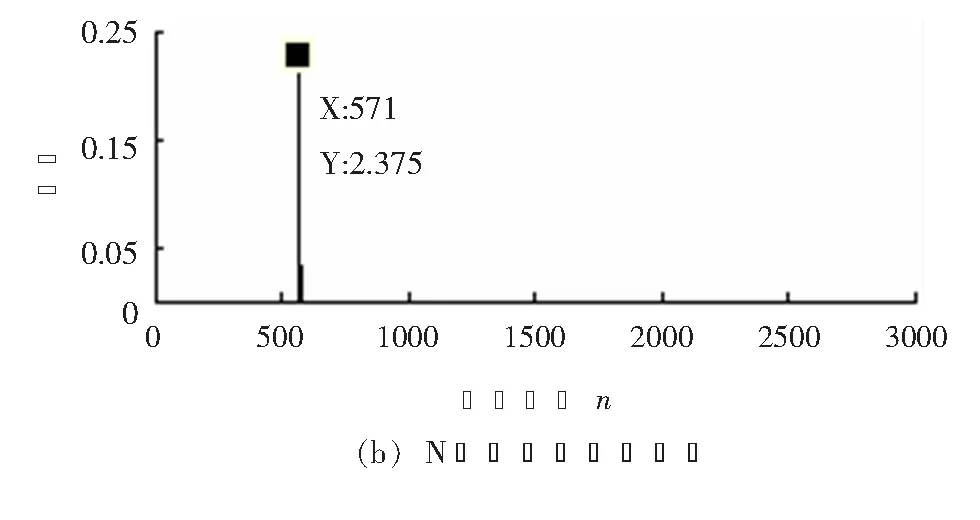
圖8 柔性形態邊緣檢測結果
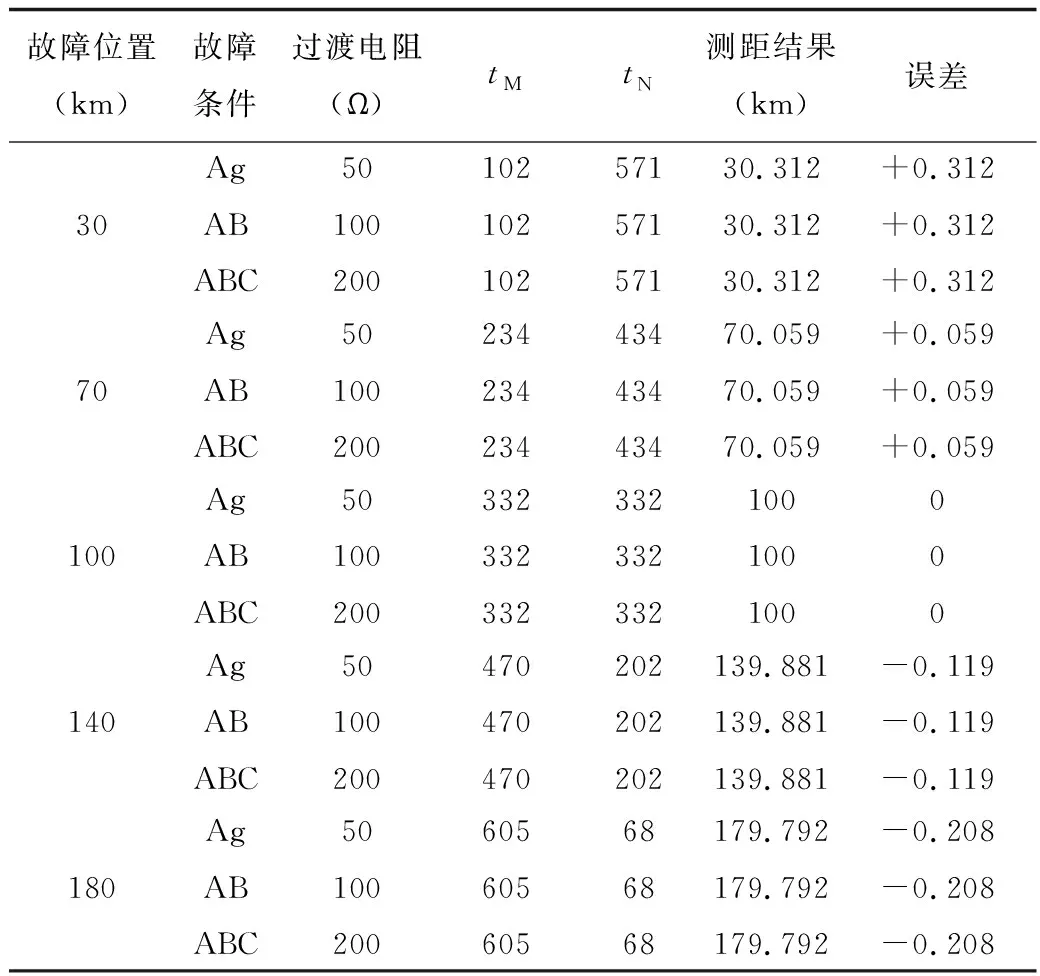
故障位置(km)故障條件過渡電阻(Ω)tMtN測距結果(km)誤差30AgABABC5010020010210210257157157130.31230.31230.312+0.312+0.312+0.31270AgABABC5010020023423423443443443470.05970.05970.059+0.059+0.059+0.059100AgABABC50100200332332332332332332100100100000140AgABABC50100200470470470202202202139.881139.881139.881-0.119-0.119-0.119180AgABABC50100200605605605686868179.792179.792179.792-0.208-0.208-0.208
4 結束語
文中提出了一種基于VMD和柔性形態學的輸電線路故障測距方法。通過將變分模態分解與柔性形態學相結合來處理信號,既可以有效去除噪聲,又可以有效地保留信號突變特征。再通過使用形態學邊緣檢測方法來提取突變點信息,從而實現輸電線路故障點定位。最后使用PSCAD搭建模型來驗證本文方法的有效性。

